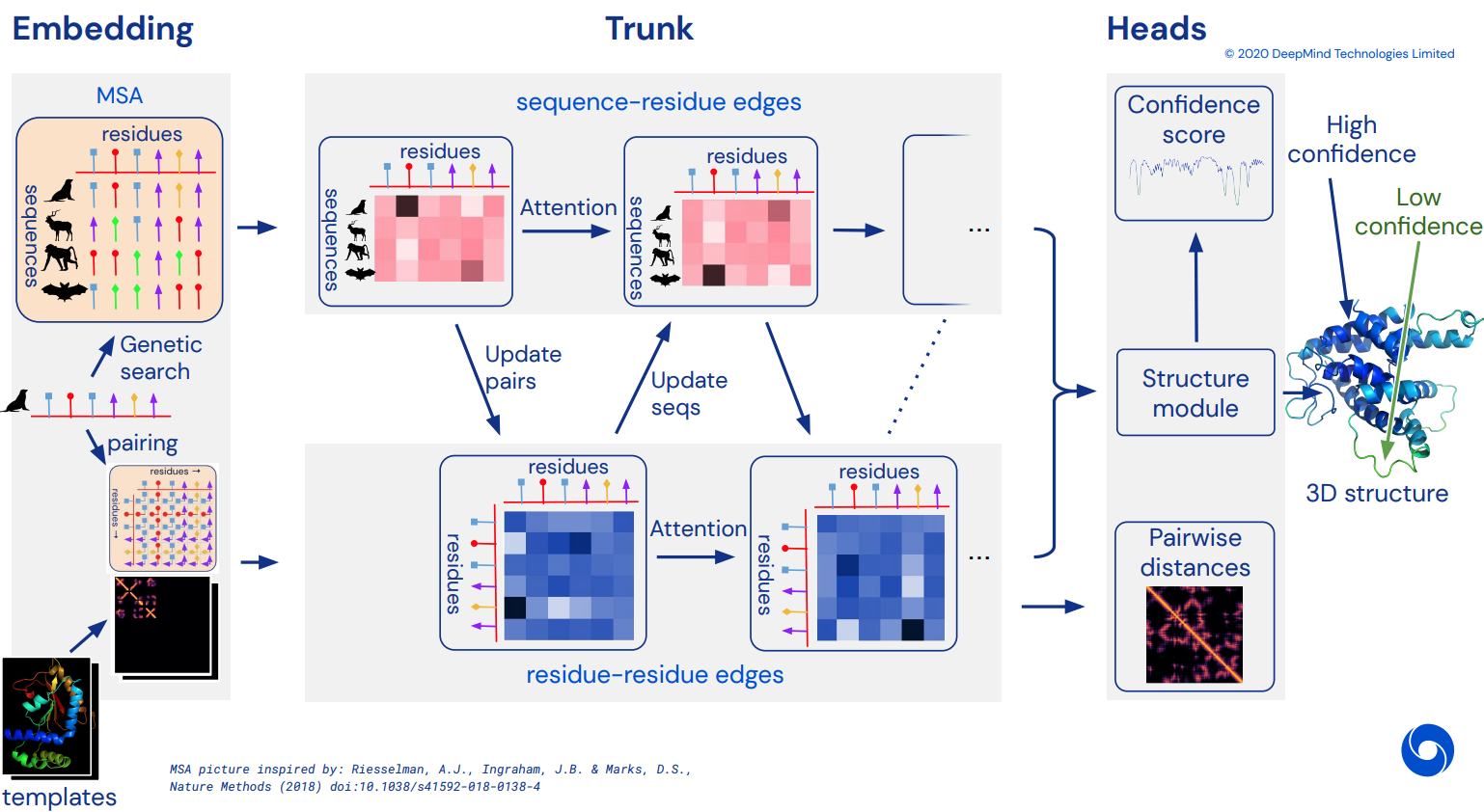
Pour finalement devenir une implémentation Pytorch non officielle d'Alphafold2, le réseau d'attention à couper le souffle qui a résolu CASP14. Sera progressivement mis en œuvre à mesure que plus de détails sur l'architecture seront publiés.
Une fois que cela sera répliqué, j'ai l'intention de replier toutes les séquences d'acides aminés disponibles in silico et de les publier sous forme de torrent académique, pour faire progresser la science. Si vous êtes intéressé par les efforts de réplication, veuillez passer par #alphafold sur ce canal Discord
Mise à jour : Deepmind a open source le code officiel dans Jax, ainsi que les poids ! Ce référentiel sera désormais orienté vers une traduction directe de pytorch avec quelques améliorations sur l'encodage positionnel
Vidéo ArxivInsights
$ pip install alphafold2-pytorchlhatsk a signalé avoir entraîné un tronc modifié de ce référentiel, en utilisant la même configuration que trRosetta, avec des résultats compétitifs
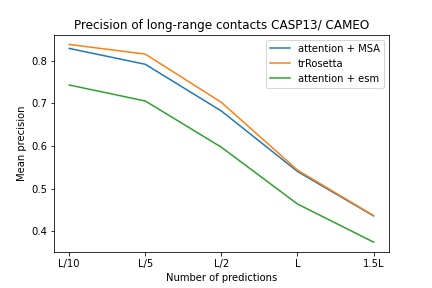
blue used the the trRosetta input (MSA -> potts -> axial attention), green used the ESM embedding (only sequence) -> tiling -> axial attention - lhatsk
Prédire le distogramme, comme Alphafold-1, mais avec attention
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
reversible = False # set this to True for fully reversible self / cross attention for the trunk
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda () # AA length of 128
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda () # MSA doesn't have to be the same length as primary sequence
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Vous pouvez également activer la prédiction pour les angles, en passant un predict_angles = True à l'initialisation. L'exemple ci-dessous serait équivalent à trRosetta mais avec une attention personnelle/croisée.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_angles = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram , theta , phi , omega = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
)
# distogram - (1, 128, 128, 37),
# theta - (1, 128, 128, 25),
# phi - (1, 128, 128, 13),
# omega - (1, 128, 128, 25) L'article récent de Fabian suggère que la transmission itérative des coordonnées dans le transformateur SE3, en partage de poids, pourrait fonctionner. J'ai décidé d'exécuter sur la base de cette idée, même si la manière dont cela fonctionne réellement reste encore à déterminer.
Vous pouvez également utiliser E(n)-Transformer ou EGNN pour le raffinement structurel.
Mise à jour : le laboratoire de Baker a montré qu'une architecture de bout en bout allant des intégrations de séquences et MSA aux transformateurs SE3 peut mieux trRosetta et combler l'écart avec Alphafold2. Nous utiliserons le Graph Transformer, qui agit sur les intégrations de troncs, pour générer l'ensemble initial de coordonnées à envoyer au réseau équivariant. (Ceci est en outre corroboré par Costa et al dans leur travail révélant les coordonnées 3D des intégrations de MSA Transformer dans un article antérieur à celui du laboratoire Baker)
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
structure_module_type = 'se3' , # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
structure_module_dim = 4 , # se3 transformer dimension
structure_module_depth = 1 , # depth
structure_module_heads = 1 , # heads
structure_module_dim_head = 16 , # dimension of heads
structure_module_refinement_iters = 2 , # number of equivariant coordinate refinement iterations
structure_num_global_nodes = 1 # number of global nodes for the structure module, only works with SE3 transformer
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue L'hypothèse sous-jacente est que le tronc fonctionne au niveau des résidus, puis constitue au niveau atomique le module de structure, qu'il s'agisse de transformateurs SE3, de transformateurs E(n) ou d'EGNN effectuant le raffinement. Cette bibliothèque utilise par défaut les 3 atomes du squelette (C, Ca, N), mais vous pouvez la configurer pour inclure tout autre atome de votre choix, y compris Cb et les chaînes latérales.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
atoms = 'backbone-with-cbeta'
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 4, 3) <-- 4 atoms per residue (C, Ca, N, Cb) Les choix valides pour atoms incluent :
backbone - 3 atomes de squelette (C, Ca, N) [par défaut]backbone-with-cbeta - 3 atomes de squelette et C bêtabackbone-with-oxygen - 3 atomes de squelette et oxygène du carboxylebackbone-with-cbeta-and-oxygen - 3 atomes de squelette avec C bêta et oxygèneall - le squelette et tous les autres atomes de la sidechainVous pouvez également passer un tenseur de forme (14,) définissant les atomes que vous souhaitez inclure
ex.
atoms = torch . tensor ([ 1 , 1 , 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 ])Ce référentiel vous offre un complément simple au réseau avec des intégrations pré-entraînées de Facebook AI. Il contient des wrappers pour les transformateurs ESM, MSA ou Protein Transformer pré-entraînés.
Il y a quelques conditions préalables. Vous devrez vous assurer que la bibliothèque apex de Nvidia est installée, car les transformateurs pré-entraînés utilisent certaines opérations fusionnées.
Ou vous pouvez essayer d'exécuter le script ci-dessous
git clone https://github.com/NVIDIA/apex
cd apex
pip install -v --disable-pip-version-check --no-cache-dir --global-option= " --cpp_ext " --global-option= " --cuda_ext " ./ Ensuite, vous devrez simplement importer et envelopper votre instance Alphafold2 avec un ESMEmbedWrapper , MSAEmbedWrapper ou ProtTranEmbedWrapper et il se chargera d'intégrer à la fois la séquence et les alignements de séquences multiples pour vous (et de la projeter aux dimensions spécifiées sur votre modèle). Rien ne doit être modifié, à l'exception de l'ajout du wrapper.
import torch
from alphafold2_pytorch import Alphafold2
from alphafold2_pytorch . embeds import MSAEmbedWrapper
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64
)
model = MSAEmbedWrapper (
alphafold2 = alphafold2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) Par défaut, même si le wrapper fournit au tronc la séquence et les intégrations MSA, elles seront additionnées avec les intégrations de jetons habituelles. Si vous souhaitez entraîner Alphafold2 sans intégrations de jetons (en vous appuyant uniquement sur des intégrations pré-entraînées), vous devrez définir disable_token_embed sur True lors de l'initialisation Alphafold2 .
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
disable_token_embed = True
) Un article de Jinbo Xu suggère qu'il n'est pas nécessaire de regrouper les distances et qu'il est possible de prédire directement la moyenne et l'écart type. Vous pouvez l'utiliser en activant un indicateur predict_real_value_distances , auquel cas, la prédiction de distance renvoyée aura une dimension de 2 pour la moyenne et l'écart type respectivement.
Si predict_coords est également activé, le MDS acceptera directement les prédictions de moyenne et d'écart type sans avoir à les calculer à partir des compartiments du distogramme.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
predict_real_value_distances = True , # set this to True
structure_module_type = 'se3' ,
structure_module_dim = 4 ,
structure_module_depth = 1 ,
structure_module_heads = 1 ,
structure_module_dim_head = 16 ,
structure_module_refinement_iters = 2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Vous pouvez ajouter des blocs convolutifs, à la fois pour la séquence principale et pour le MSA, en définissant simplement un argument de mot-clé supplémentaire use_conv = True
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37)Les noyaux convolutifs suivent l'exemple de cet article, combinant les noyaux 1D et 2D dans un bloc de type resnet. Vous pouvez entièrement personnaliser les noyaux en tant que tels.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
conv_seq_kernels = (( 9 , 1 ), ( 1 , 9 ), ( 3 , 3 )), # kernels for N x N primary sequence
conv_msa_kernels = (( 1 , 9 ), ( 3 , 3 )), # kernels for {num MSAs} x N MSAs
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Vous pouvez également effectuer une dilatation de cycle avec un argument de mot-clé supplémentaire. La dilatation par défaut est 1 pour toutes les couches.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
dilations = ( 1 , 3 , 5 ) # cycle between dilations of 1, 3, 5
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Enfin, au lieu de suivre le modèle de convolutions, d'auto-attention, d'attention croisée par répétition de profondeur, vous pouvez personnaliser l'ordre de votre choix avec le mot-clé custom_block_types .
ex. Un réseau dans lequel vous effectuez principalement des convolutions en premier, suivies de blocs d'auto-attention + d'attention croisée
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
heads = 8 ,
dim_head = 64 ,
custom_block_types = (
* (( 'conv' ,) * 6 ),
* (( 'self' , 'cross' ) * 6 )
)
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Vous pouvez vous entraîner avec Sparse Attention de Microsoft Deepspeed, mais vous devrez supporter le processus d'installation. C'est en deux étapes.
Tout d’abord, vous devez installer Deepspeed avec Sparse Attention
$ sh install_deepspeed.sh Ensuite, vous devez installer le package pip triton
$ pip install tritonSi les deux opérations ci-dessus ont réussi, vous pouvez désormais vous entraîner avec Sparse Attention !
Malheureusement, l’attention éparse n’est prise en charge que pour l’attention personnelle et non pour l’attention croisée. J'apporterai une solution différente pour rendre l'attention croisée performante.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
max_seq_len = 2048 , # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
sparse_self_attn = ( True , False ) * 6 # interleave sparse and full attention for all 12 layers
). cuda ()J'ai également ajouté l'une des meilleures variantes d'attention linéaire, dans l'espoir d'alléger le fardeau de l'attention croisée. Personnellement, je n'ai pas trouvé que Performer fonctionnait aussi bien, mais comme dans l'article ils rapportaient des chiffres corrects pour les références protéiques, j'ai pensé que je l'inclurais et permettrais à d'autres d'expérimenter.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = True # simply set this to True to use Performer for all cross attention
). cuda ()Vous pouvez également spécifier les calques exacts sur lesquels vous souhaitez utiliser l'attention linéaire en passant un tuple de la même longueur que la profondeur.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = ( True , False ) * 3 # interleave linear and full attention
). cuda ()Cet article suggère que si vous avez des requêtes ou des contextes qui ont des axes définis (par exemple une image), vous pouvez réduire la quantité d'attention nécessaire en faisant la moyenne sur ces axes (hauteur et largeur) et en concaténant les axes moyennés en une seule séquence. Vous pouvez activer cette technique comme technique d'économie de mémoire pour l'attention croisée, en particulier pour la séquence principale.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_kron_primary = True # make sure primary sequence undergoes the kronecker operator during cross attention
). cuda () Vous pouvez également appliquer le même opérateur aux MSA lors de l'attention croisée avec le flag cross_attn_kron_msa , si vos MSA sont alignés et de même largeur.
Faire
Pour économiser de la mémoire pour une attention croisée, vous pouvez définir un taux de compression pour les clés/valeurs, en suivant le schéma présenté dans cet article. Un taux de compression de 2 à 4 est généralement acceptable.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_compress_ratio = 3
). cuda ()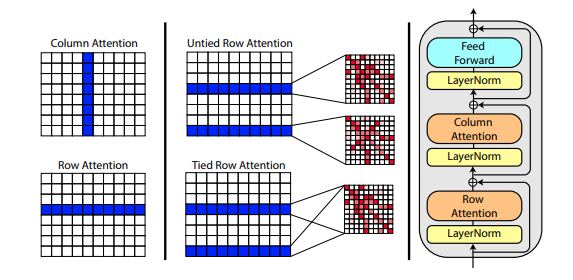
Un nouvel article de Roshan Rao propose d'utiliser l'attention axiale pour le pré-entraînement sur les MSA. Compte tenu des bons résultats, ce référentiel utilisera le même schéma dans le tronc, spécifiquement pour l'auto-attention MSA.
Vous pouvez également lier les attentions de ligne du MSA avec le paramètre msa_tie_row_attn = True lors de l'initialisation d' Alphafold2 . Cependant, pour utiliser cela, vous devez vous assurer que si vous avez un nombre impair de MSA par séquence principale, que le masque MSA est correctement défini sur False pour les lignes non utilisées.
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
msa_tie_row_attn = True # just set this to true
)Le traitement des modèles s'effectue également en grande partie avec une attention axiale, avec une attention croisée selon la dimension du nombre de modèles. Cela suit en grande partie le même schéma que celui de la récente approche axée sur toute l'attention en matière de classification vidéo, comme indiqué ici.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randint ( 0 , 37 , ( 1 , 2 , 16 , 3 )). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_coors = templates_coors ,
templates_mask = templates_mask
)Si des informations de chaîne latérale sont également présentes, sous la forme du vecteur unitaire entre les coordonnées C et C-alpha de chaque résidu, vous pouvez également les transmettre comme suit.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randn ( 1 , 2 , 16 , 3 ). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
templates_sidechains = torch . randn ( 1 , 2 , 16 , 3 ). cuda () # unit vectors of difference of C and C-alpha coordinates
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_mask = templates_mask ,
templates_coors = templates_coors ,
templates_sidechains = templates_sidechains
)J'ai préparé une réimplémentation de SE3 Transformer, comme l'explique Fabian Fuchs dans un article de blog spéculatif.
De plus, un nouvel article de Victor et Welling utilise des fonctionnalités invariantes pour l'équivariance E(n), atteignant SOTA et surpassant SE3 Transformer sur un certain nombre de points de référence, tout en étant beaucoup plus rapide. J'ai repris les idées principales de cet article et je l'ai modifié pour devenir un transformateur (attention accrue aux fonctionnalités et aux mises à jour des coordonnées).
Les trois réseaux équivariants ci-dessus ont été intégrés et peuvent être utilisés dans le référentiel pour le raffinement des coordonnées atomiques en définissant simplement un hyperparamètre structure_module_type .
se3 SE3 Transformateur
egnn EGNN
en E(n)-Transformateur
D'intérêt pour les lecteurs, chacun des trois cadres a également été validé par des chercheurs sur des problèmes connexes.
$ python setup.py test Cette bibliothèque utilisera le travail impressionnant de Jonathan King dans ce référentiel. Merci Jonathan !
Nous avons également les données MSA, toutes d'une valeur d'environ 3,5 To, téléchargées et hébergées par Archivist, propriétaire du projet The-Eye. (Ils hébergent également les données et les modèles pour Eleuther AI) Veuillez envisager un don si vous les trouvez utiles.
$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txthttps://xukui.cn/alphafold2.html
https://moalquraishi.wordpress.com/2020/12/08/alphafold2-casp14-it-feels-like-ones-child-has-left-home/

https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf
https://pubmed.ncbi.nlm.nih.gov/33637700/
Présentation tFold, des laboratoires Tencent AI
cd downloads_folder > pip install pyrosetta_wheel_filename.whlOpenMM Ambre
@misc { unpublished2021alphafold2 ,
title = { Alphafold2 } ,
author = { John Jumper } ,
year = { 2020 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @article { Rao2021.02.12.430858 ,
author = { Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander } ,
title = { MSA Transformer } ,
year = { 2021 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858 } ,
journal = { bioRxiv }
} @article { Rives622803 ,
author = { Rives, Alexander and Goyal, Siddharth and Meier, Joshua and Guo, Demi and Ott, Myle and Zitnick, C. Lawrence and Ma, Jerry and Fergus, Rob } ,
title = { Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences } ,
year = { 2019 } ,
doi = { 10.1101/622803 } ,
publisher = { Cold Spring Harbor Laboratory } ,
journal = { bioRxiv }
} @article { Elnaggar2020.07.12.199554 ,
author = { Elnaggar, Ahmed and Heinzinger, Michael and Dallago, Christian and Rehawi, Ghalia and Wang, Yu and Jones, Llion and Gibbs, Tom and Feher, Tamas and Angerer, Christoph and Steinegger, Martin and BHOWMIK, DEBSINDHU and Rost, Burkhard } ,
title = { ProtTrans: Towards Cracking the Language of Life{textquoteright}s Code Through Self-Supervised Deep Learning and High Performance Computing } ,
elocation-id = { 2020.07.12.199554 } ,
year = { 2021 } ,
doi = { 10.1101/2020.07.12.199554 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554.full.pdf } ,
journal = { bioRxiv }
} @misc { king2020sidechainnet ,
title = { SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning } ,
author = { Jonathan E. King and David Ryan Koes } ,
year = { 2020 } ,
eprint = { 2010.08162 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { alquraishi2019proteinnet ,
title = { ProteinNet: a standardized data set for machine learning of protein structure } ,
author = { Mohammed AlQuraishi } ,
year = { 2019 } ,
eprint = { 1902.00249 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { gomez2017reversible ,
title = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
author = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
year = { 2017 } ,
eprint = { 1707.04585 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CV }
} @misc { fuchs2021iterative ,
title = { Iterative SE(3)-Transformers } ,
author = { Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner } ,
year = { 2021 } ,
eprint = { 2102.13419 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { satorras2021en ,
title = { E(n) Equivariant Graph Neural Networks } ,
author = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
year = { 2021 } ,
eprint = { 2102.09844 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { su2021roformer ,
title = { RoFormer: Enhanced Transformer with Rotary Position Embedding } ,
author = { Jianlin Su and Yu Lu and Shengfeng Pan and Bo Wen and Yunfeng Liu } ,
year = { 2021 } ,
eprint = { 2104.09864 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CL }
} @article { Gao_2020 ,
title = { Kronecker Attention Networks } ,
ISBN = { 9781450379984 } ,
url = { http://dx.doi.org/10.1145/3394486.3403065 } ,
DOI = { 10.1145/3394486.3403065 } ,
journal = { Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining } ,
publisher = { ACM } ,
author = { Gao, Hongyang and Wang, Zhengyang and Ji, Shuiwang } ,
year = { 2020 } ,
month = { Jul }
} @article { Si2021.05.10.443415 ,
author = { Si, Yunda and Yan, Chengfei } ,
title = { Improved protein contact prediction using dimensional hybrid residual networks and singularity enhanced loss function } ,
elocation-id = { 2021.05.10.443415 } ,
year = { 2021 } ,
doi = { 10.1101/2021.05.10.443415 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415.full.pdf } ,
journal = { bioRxiv }
} @article { Costa2021.06.02.446809 ,
author = { Costa, Allan and Ponnapati, Manvitha and Jacobson, Joseph M. and Chatterjee, Pranam } ,
title = { Distillation of MSA Embeddings to Folded Protein Structures with Graph Transformers } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.02.446809 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809.full.pdf } ,
journal = { bioRxiv }
} @article { Baek2021.06.14.448402 ,
author = { Baek, Minkyung and DiMaio, Frank and Anishchenko, Ivan and Dauparas, Justas and Ovchinnikov, Sergey and Lee, Gyu Rie and Wang, Jue and Cong, Qian and Kinch, Lisa N. and Schaeffer, R. Dustin and Mill{'a}n, Claudia and Park, Hahnbeom and Adams, Carson and Glassman, Caleb R. and DeGiovanni, Andy and Pereira, Jose H. and Rodrigues, Andria V. and van Dijk, Alberdina A. and Ebrecht, Ana C. and Opperman, Diederik J. and Sagmeister, Theo and Buhlheller, Christoph and Pavkov-Keller, Tea and Rathinaswamy, Manoj K and Dalwadi, Udit and Yip, Calvin K and Burke, John E and Garcia, K. Christopher and Grishin, Nick V. and Adams, Paul D. and Read, Randy J. and Baker, David } ,
title = { Accurate prediction of protein structures and interactions using a 3-track network } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.14.448402 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402.full.pdf } ,
journal = { bioRxiv }
}