@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}Saviez-vous que neurodiffeq prend en charge les ensembles de solutions et peut être utilisé pour résoudre des problèmes inverses ? Voir ici !
? Vous connaissez déjà le neurodifféq ? ? Accédez à la FAQ.
neurodiffeq est un package permettant de résoudre des équations différentielles avec des réseaux de neurones. Les équations différentielles sont des équations qui relient une fonction à ses dérivées. Ils émergent dans divers domaines scientifiques et techniques. Traditionnellement, ces problèmes peuvent être résolus par des méthodes numériques (par exemple différences finies, éléments finis). Bien que ces méthodes soient efficaces et adéquates, leur expressibilité est limitée par leur représentation fonctionnelle. Il serait intéressant de pouvoir calculer des solutions pour des équations différentielles continues et différentiables.
En tant qu'approximateurs de fonctions universelles, il a été démontré que les réseaux de neurones artificiels ont le potentiel de résoudre des équations différentielles ordinaires (ODE) et des équations aux dérivées partielles (PDE) avec certaines conditions initiales/aux limites. L'objectif de neurodiffeq est de mettre en œuvre ces techniques existantes d'utilisation de l'ANN pour résoudre des équations différentielles de manière à permettre au logiciel d'être suffisamment flexible pour travailler sur un large éventail de problèmes définis par l'utilisateur.
Comme la plupart des bibliothèques standards, neurodiffeq est hébergée sur PyPI. Pour installer la dernière version stable,
pip install -U neurodiffeq # '-U' signifie mise à jour vers la dernière version
Vous pouvez également installer la bibliothèque manuellement pour obtenir un accès anticipé à nos nouvelles fonctionnalités. C'est la méthode recommandée pour les développeurs qui souhaitent contribuer à la bibliothèque.
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && pip install -r exigences pip installer. # Pour apporter des modifications à la bibliothèque, utilisez `pip install -e .`pytest tests/ # Exécutez les tests. Facultatif.
Nous serons heureux de vous aider pour toute question. En attendant, vous pouvez consulter la FAQ.
Pour consulter les didacticiels complets et la documentation de neurodiffeq , veuillez consulter la documentation officielle.
En plus des documentations, nous avons récemment réalisé une vidéo de démonstration rapide avec des diapositives.
depuis neurodiffeq importer difffrom neurodiffeq.solvers importer Solver1D, Solver2Dfrom neurodiffeq.conditions importer IVP, DirichletBVP2Dfrom neurodiffeq.networks importer FCNN, SinActv
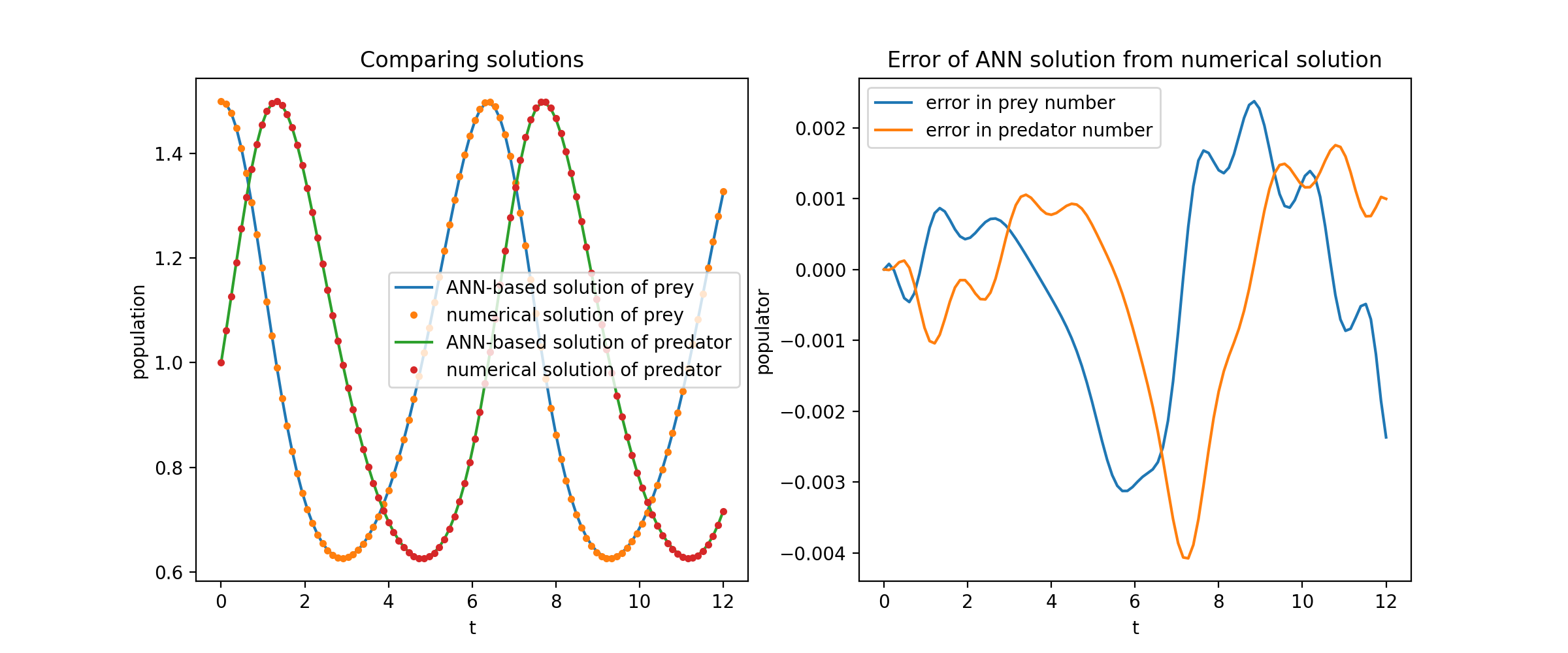
Ici, nous résolvons un système non linéaire de deux ODE, connu sous le nom d’équations de Lotka – Volterra. Il existe deux fonctions inconnues ( u et v ) et une seule variable indépendante ( t ).
def ode_system(u, v, t) : return [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]conditions = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]solver = Solver1D(ode_system, conditions, t_min=0.1, t_max=12.0, nets=nets)solver.fit(max_epochs=3000)solution = solver.get_solution()
solution est un objet appelable, vous pouvez lui transmettre des tableaux numpy ou des tenseurs torch comme
u, v = solution(t, to_numpy=True) # t peut être np.ndarray ou torch.Tensor
Tracer u et v par rapport à leurs solutions analytiques donne quelque chose comme :
Ici, nous résolvons une équation de Laplace avec des conditions aux limites de Dirichlet sur un rectangle. Notez que nous choisissons l’équation de Laplace pour sa simplicité de calcul de la solution analytique. En pratique, vous pouvez tenter n'importe quelle PDE non linéaire et chaotique , à condition de bien régler le solveur.
La résolution d'un système PDE 2D est assez similaire à la résolution d'EDO, sauf qu'il existe deux variables x et y pour les problèmes de valeurs limites ou x et t pour les problèmes de valeurs limites initiales, qui sont toutes deux prises en charge.
def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: torch. sin(np.pi*y),x_max=1, x_max_val=lambda y : 0, y_min=0, y_min_val=lambda x : 0, y_max=1, y_max_val=lambda x : 0,
)
]nets = [FCNN(n_input_units=2, n_output_units=1, Hidden_units=(512,))]solver = Solver2D(pde_system, conditions, xy_min=(0, 0), xy_max=(1, 1), nets=nets) solveur.fit(max_epochs=2000)solution = solveur.get_solution() La signature de solution pour un PDE 2D est légèrement différente de celle d'une ODE. Encore une fois, il utilise soit des tableaux numpy, soit des tenseurs de torche.
u = solution (x, y, to_numpy=True)
L'évaluation de u sur [0,1] × [0,1] donne les tracés suivants
| Solution basée sur ANN | Résidu de PDE |
|---|---|
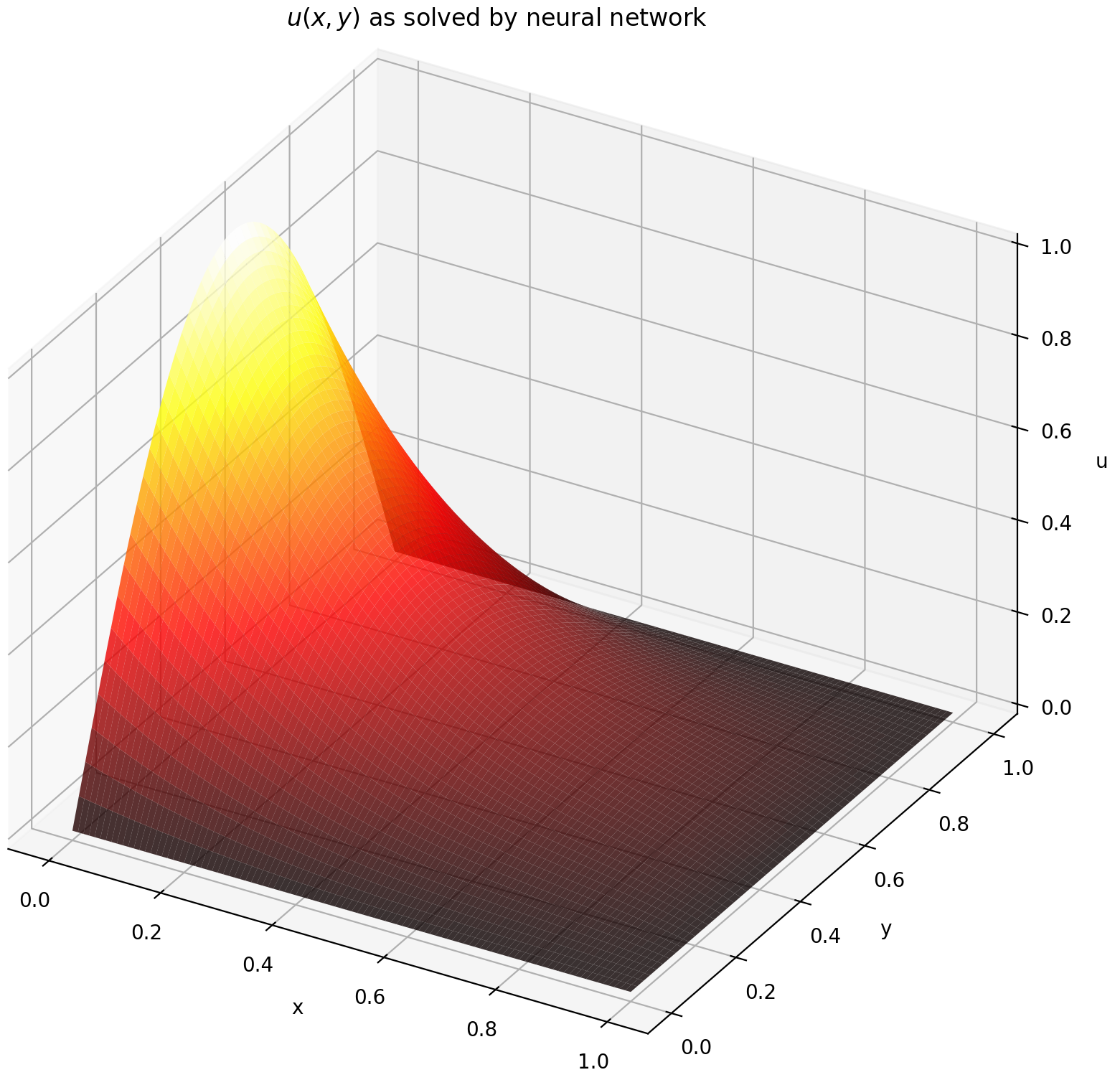 | 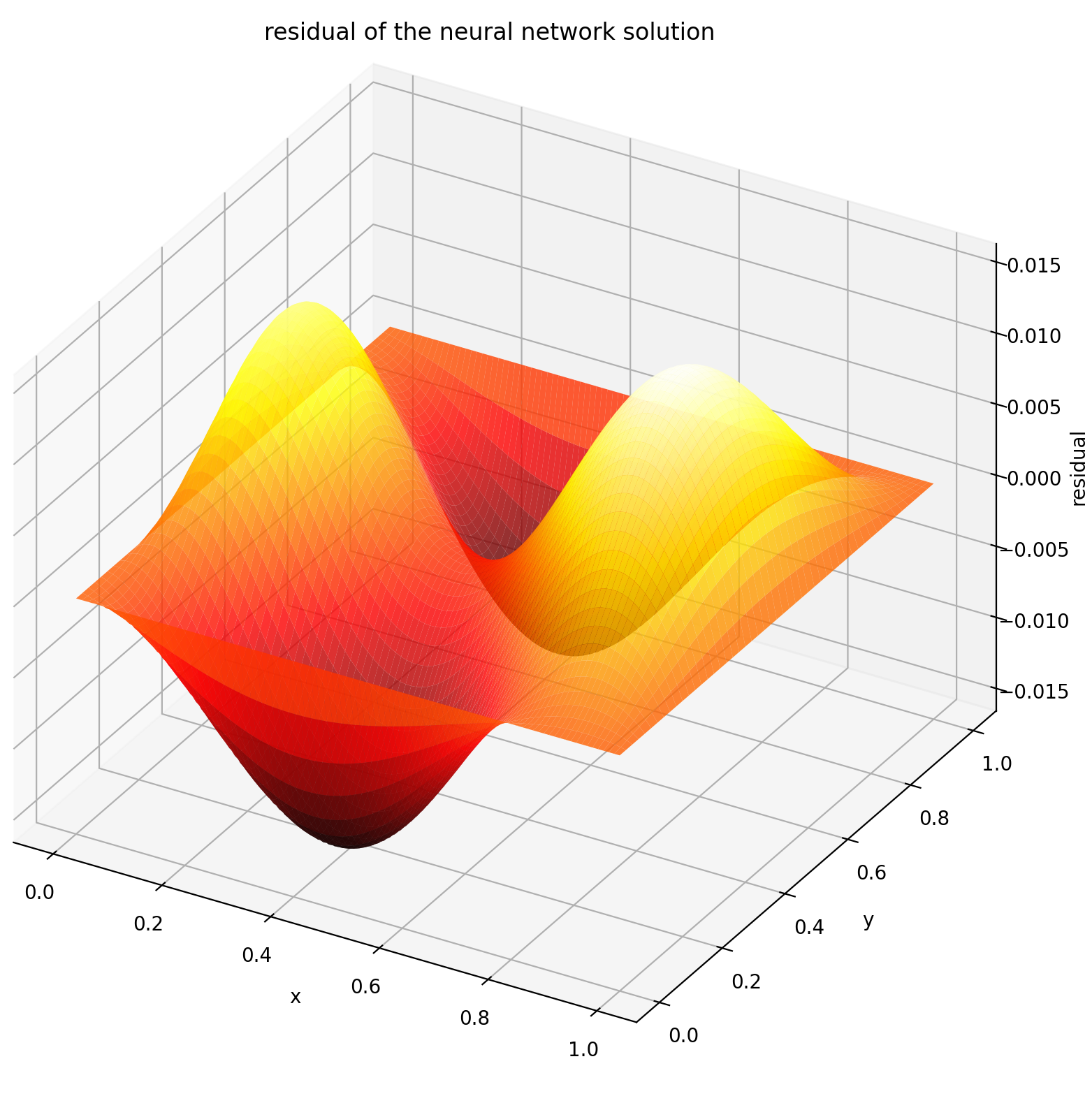 |
Un moniteur est un outil permettant de visualiser les solutions PDE/ODE ainsi que l'historique des pertes et les métriques personnalisées pendant la formation. Les utilisateurs de Jupyter Notebooks doivent exécuter la magie %matplotlib notebook . Pour les utilisateurs de Jupyter Lab, essayez %matplotlib widget .
à partir de neurodiffeq.monitors import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
Vous devriez voir les tracés se mettre à jour toutes les 100 époques ainsi qu'à la dernière époque , affichant deux tracés — un pour la visualisation de la solution sur l'intervalle [0,12] et l'autre pour l'historique des pertes (entraînement et validation).
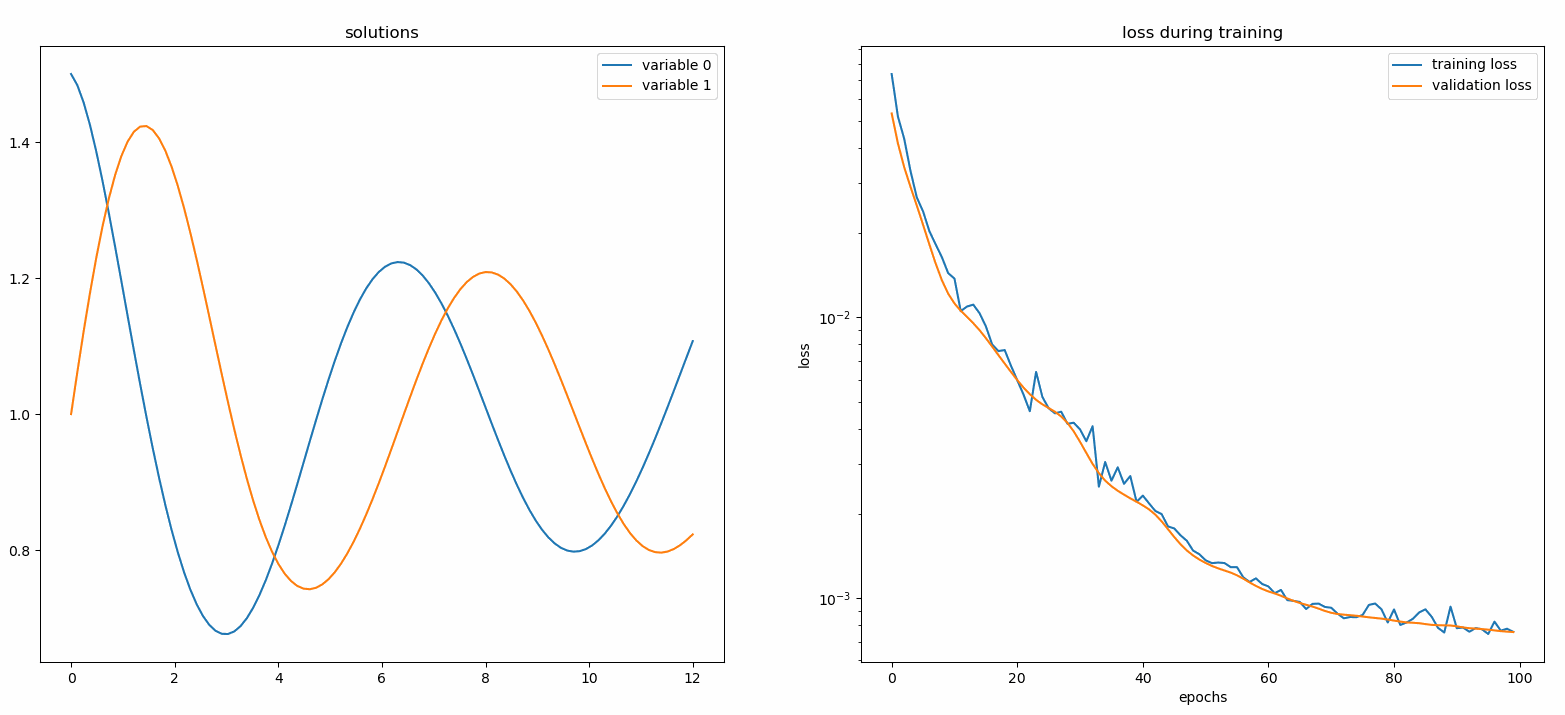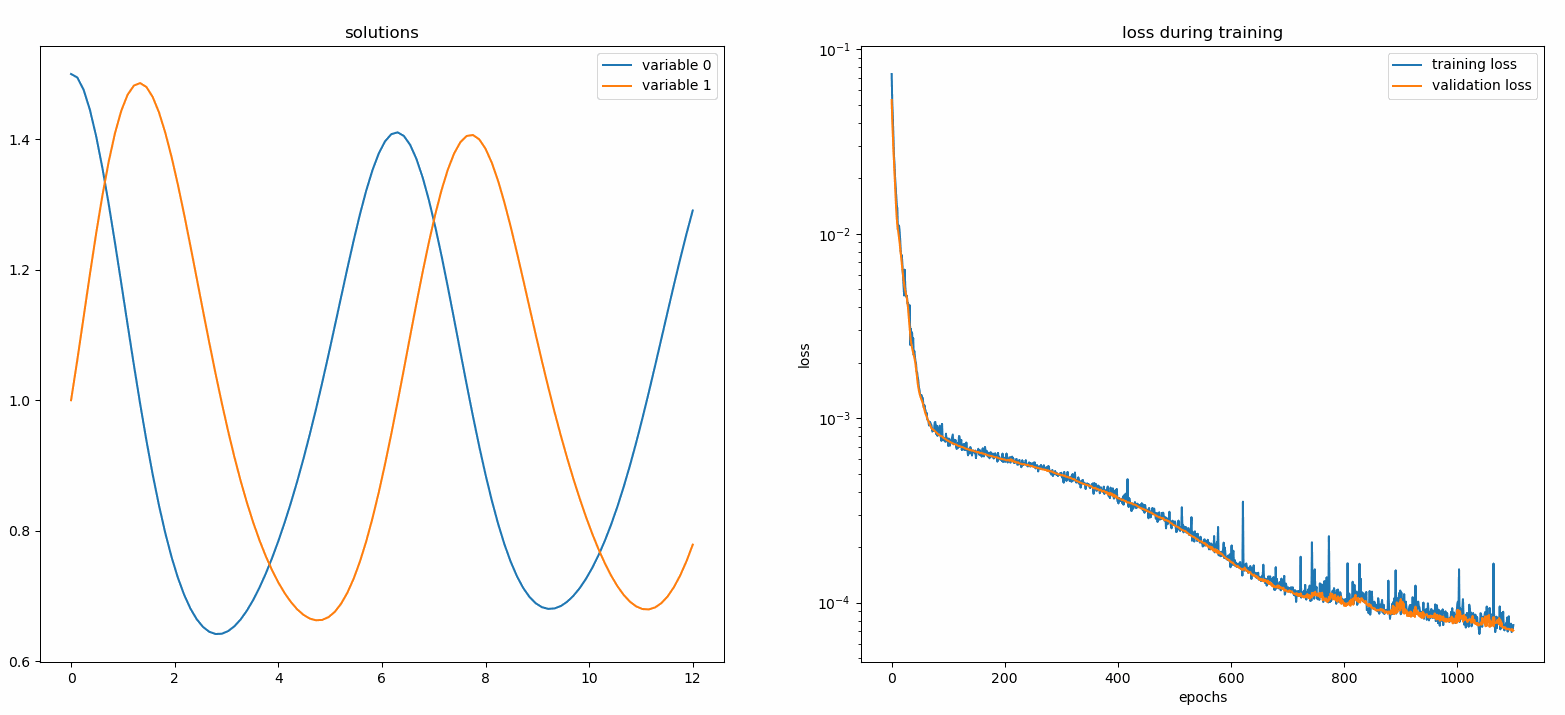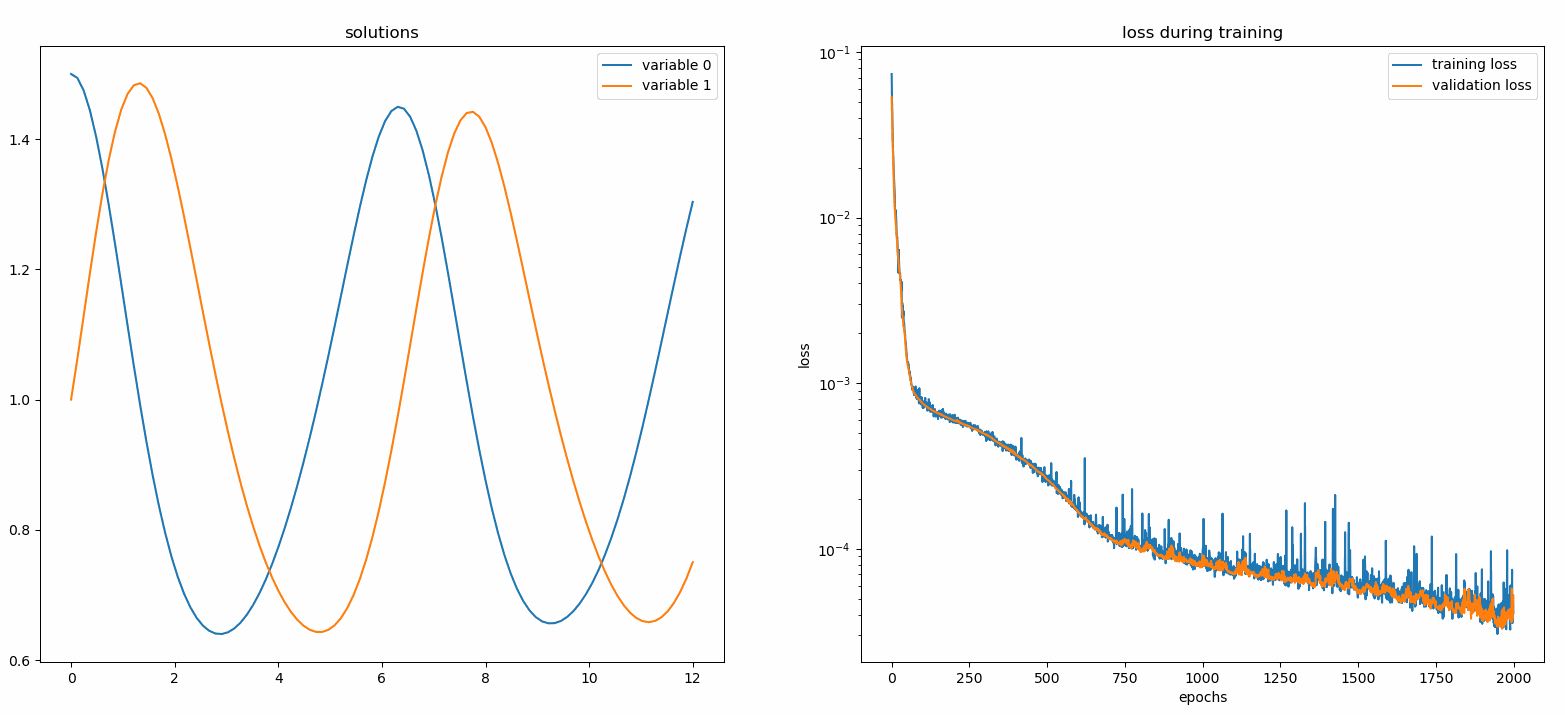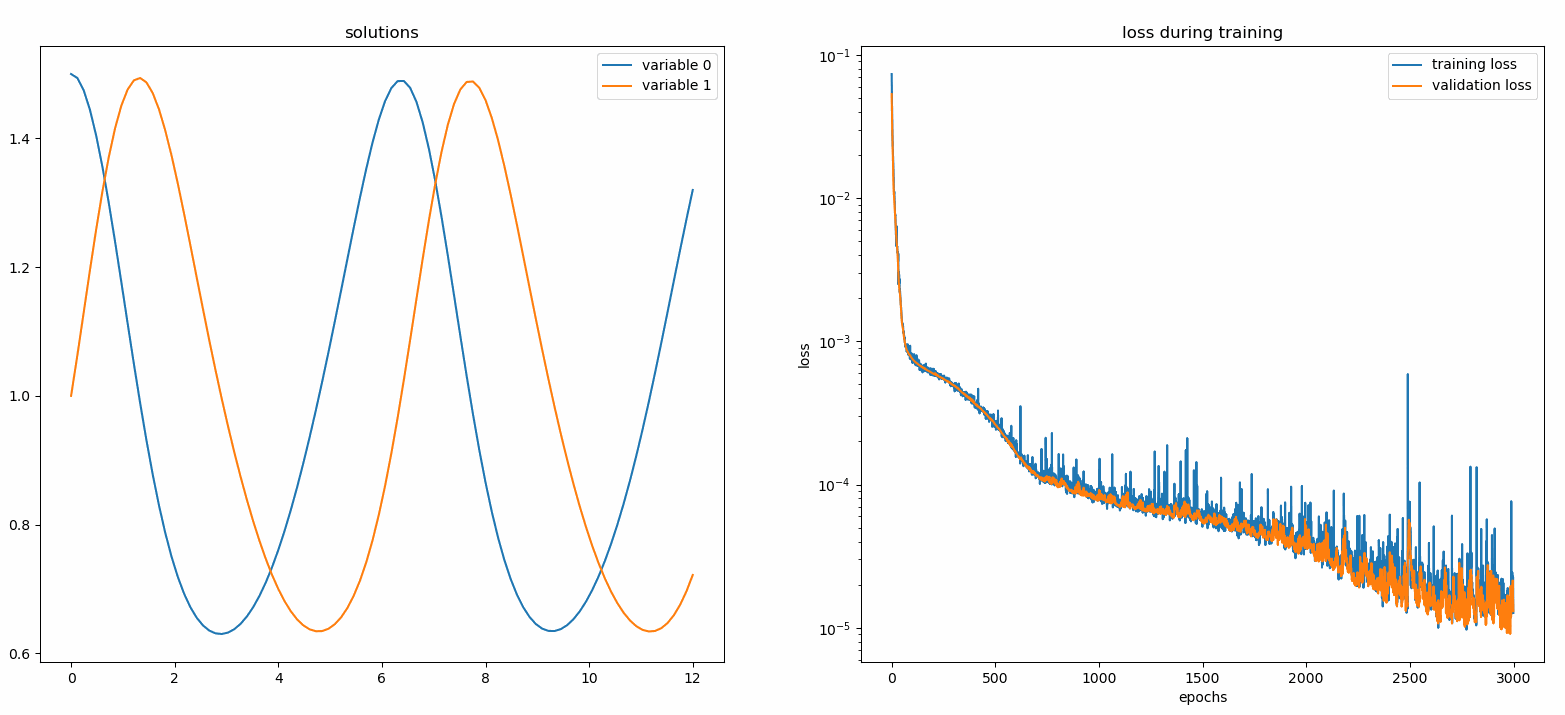
Pour plus de commodité, nous avons implémenté un réseau neuronal FCNN – entièrement connecté, dont les unités cachées et les fonctions d'activation peuvent être personnalisées.
depuis neurodiffeq.networks import FCNN# Par défaut : n_input_units=1, n_output_units=1, Hidden_units=[32, 32], activation=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., Hidden_units=[ ..., ..., ...], activation=...) ...réseaux = [net1, net2, ...]
FCNN est généralement un bon point de départ. Pour les utilisateurs avancés, les solveurs sont compatibles avec n’importe quel torch.nn.Module personnalisé. Les seules contraintes sont :
Les modules prennent un tenseur de forme (None, n_coords) et les sorties un tenseur de forme (None, 1) .
Il doit y avoir un total de modules n_funcs dans nets pour être transmis à solver = Solver(..., nets=nets) .
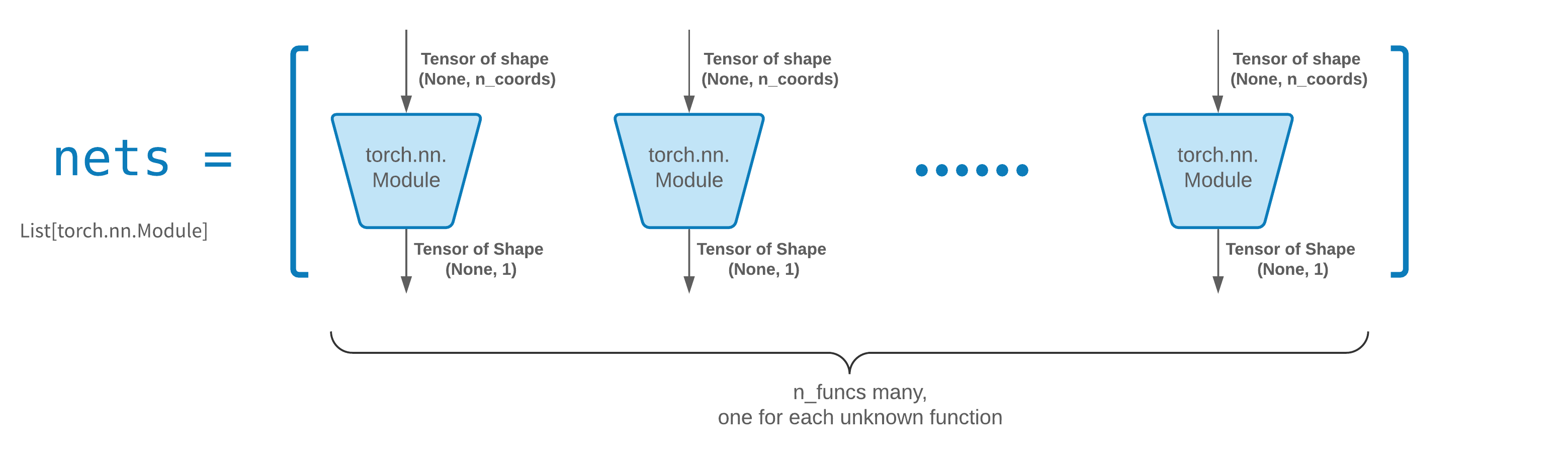
En fait, neurodiffeq possède une fonctionnalité single_net qui n'obéit pas aux règles ci-dessus, qui ne seront pas abordées ici.
Lisez le didacticiel PyTorch sur la création de votre propre architecture de réseau (alias module).
L'apprentissage par transfert se fait facilement en sérialisant old_solver.nets (une liste de modules Torch) sur le disque, puis en les chargeant et en les transmettant à un nouveau solveur :
old_solver.fit(max_epochs=...)# ... dump `old_solver.nets` sur le disque# ... charge les réseaux à partir du disque, stockez-les dans une variable `loaded_nets` new_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
Nous travaillons actuellement sur des fonctions wrapper pour sauvegarder/charger les réseaux et autres variables internes des Solvers. En attendant, vous pouvez lire le tutoriel PyTorch sur la sauvegarde et le chargement de vos réseaux.
En neurodiffeq, les réseaux sont entraînés en minimisant les pertes (résidus ODE/PDE) évalués sur un ensemble de points du domaine. Les points sont rééchantillonnés de manière aléatoire à chaque fois. Pour contrôler le nombre, la distribution et le domaine englobant des points échantillonnés, vous pouvez spécifier vos propres generator de formation/validation.
à partir de neurodiffeq.generators import Generator1D# Par défaut t_min=0.0, t_max=1.0, method='uniform', noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. ., noise_std=...)g2 = Générateur1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
Voici quelques exemples de distributions d'un Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
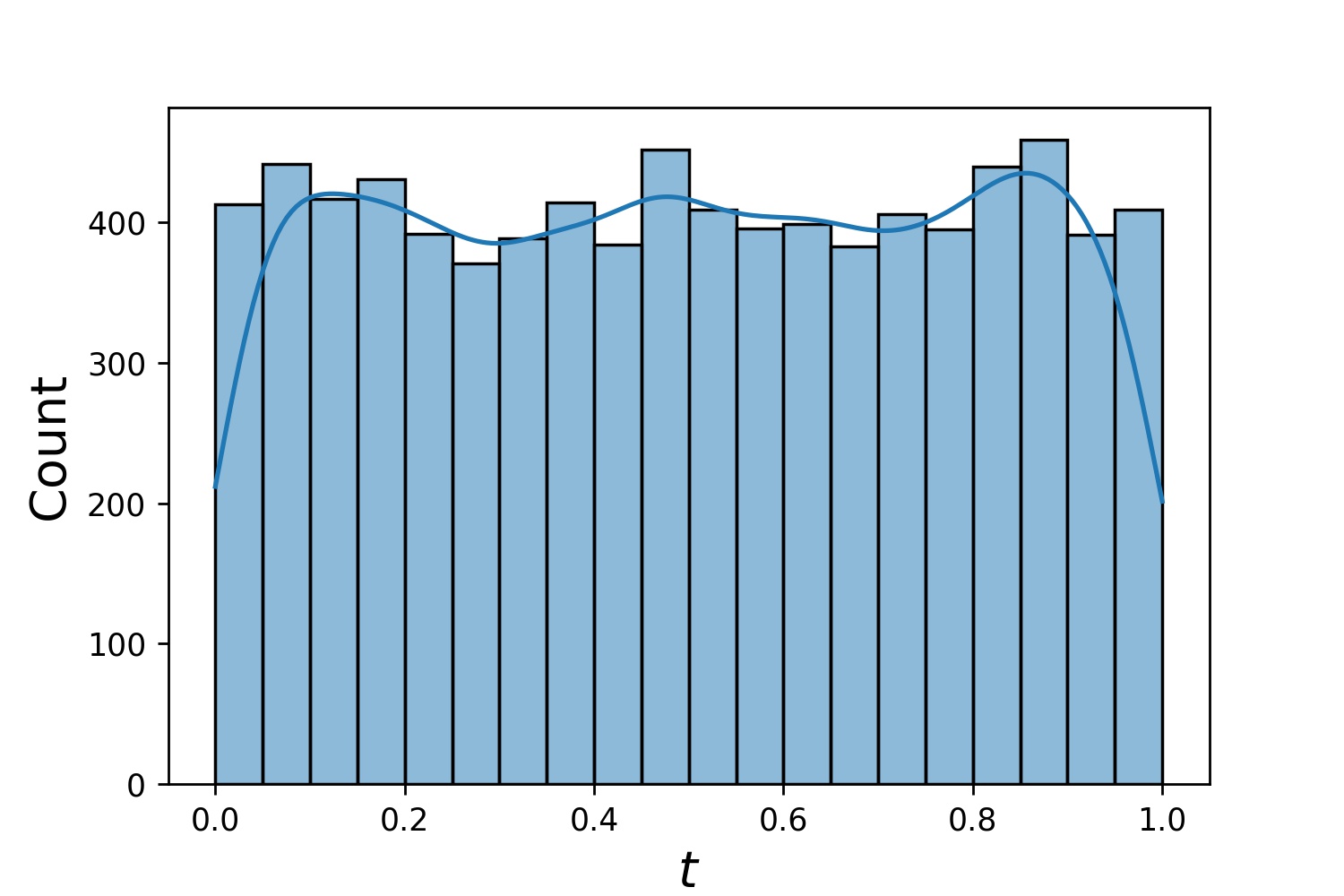 | 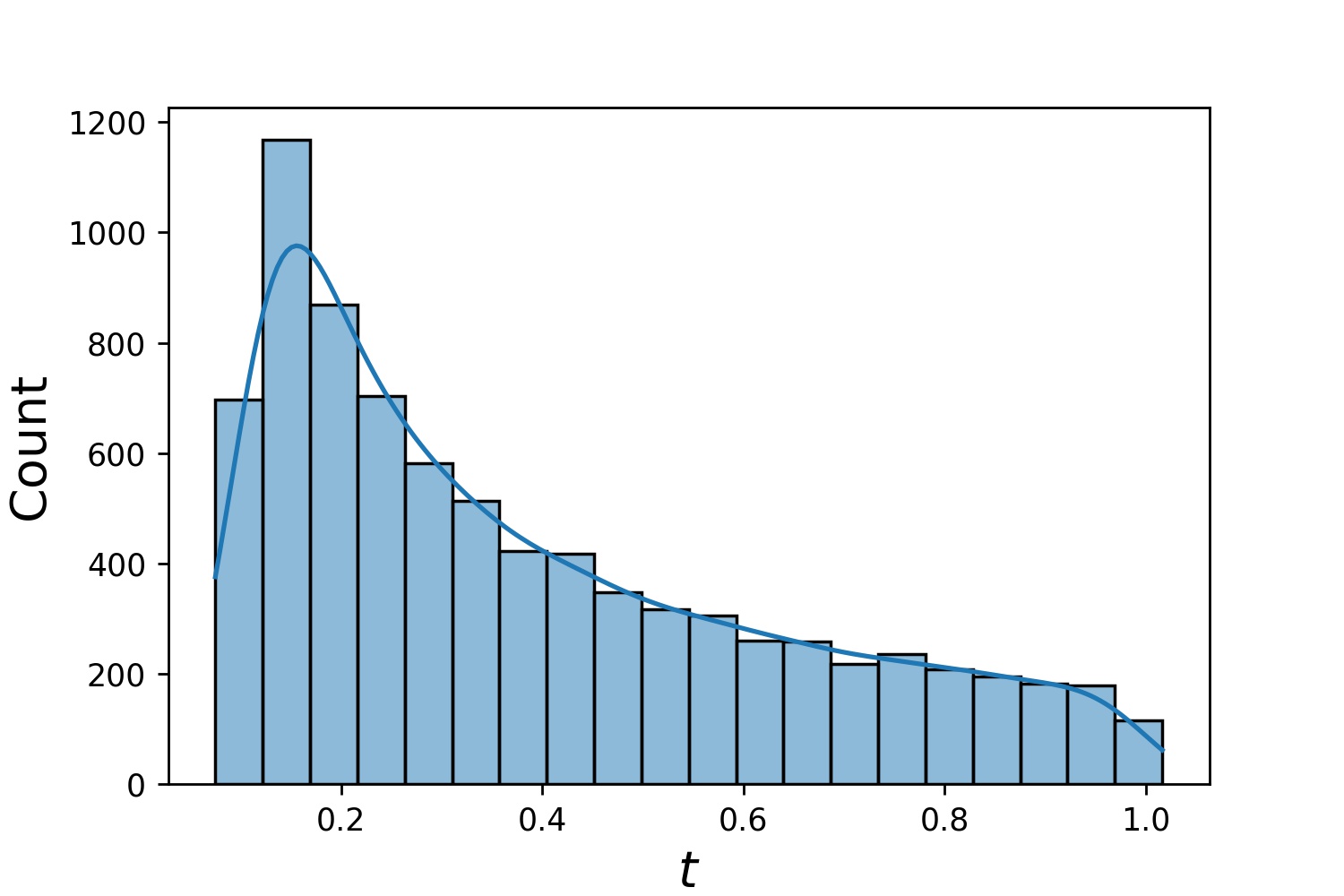 |
Notez que lorsque train_generator et valid_generator sont spécifiés, t_min et t_max peuvent être omis dans Solver1D(...) . En fait, même si vous transmettez t_min , t_max , train_generator , valid_generator ensemble, les t_min et t_max seront toujours ignorés.
Une autre fonctionnalité intéressante des générateurs est que vous pouvez les concaténer, par exemple
g1 = Générateur2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Générateur2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))g = g1 + g2
Ici, g sera un générateur qui génère les échantillons combinés de g1 et g2
g1 | g2 | g1 + g2 |
|---|---|---|
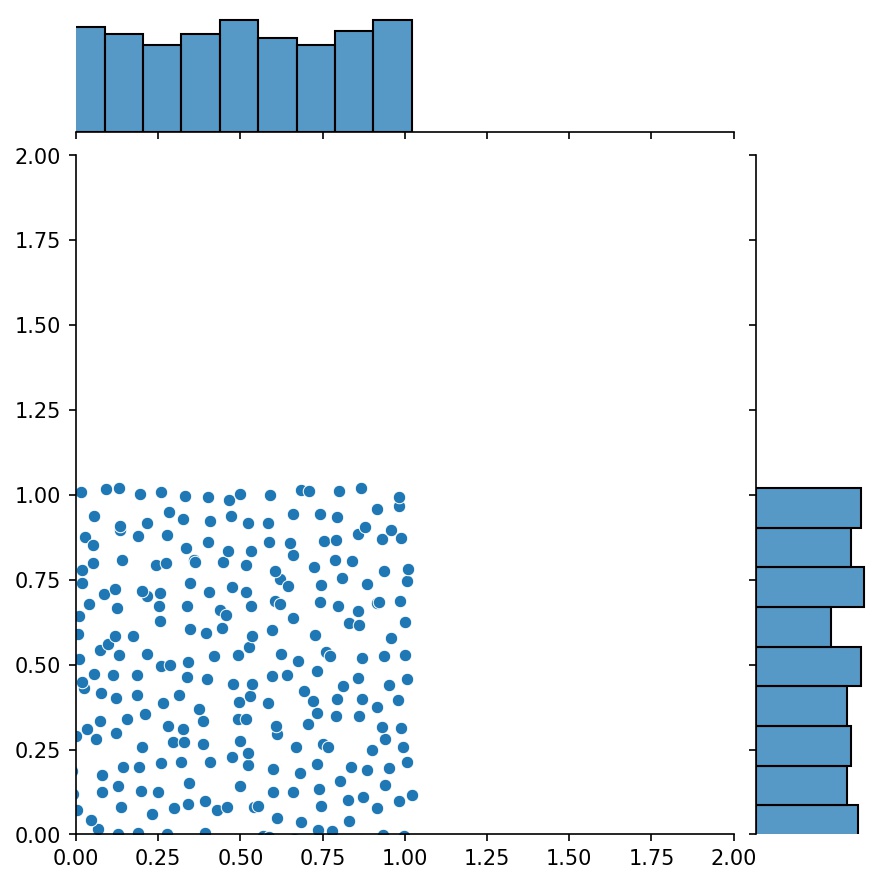 | 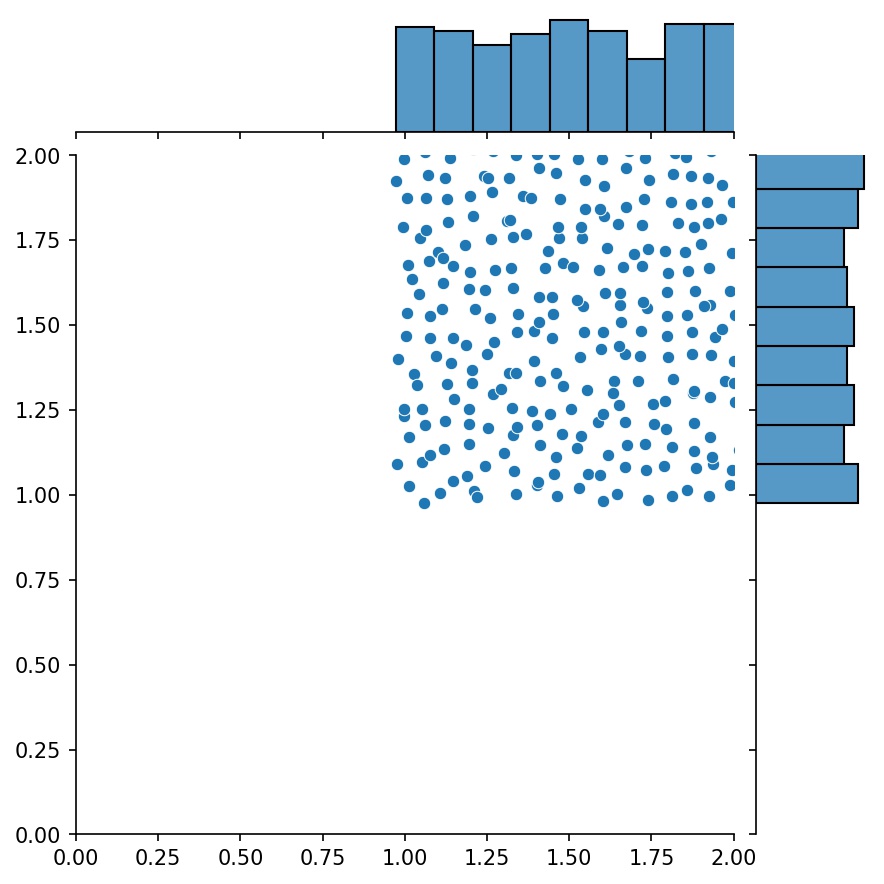 | 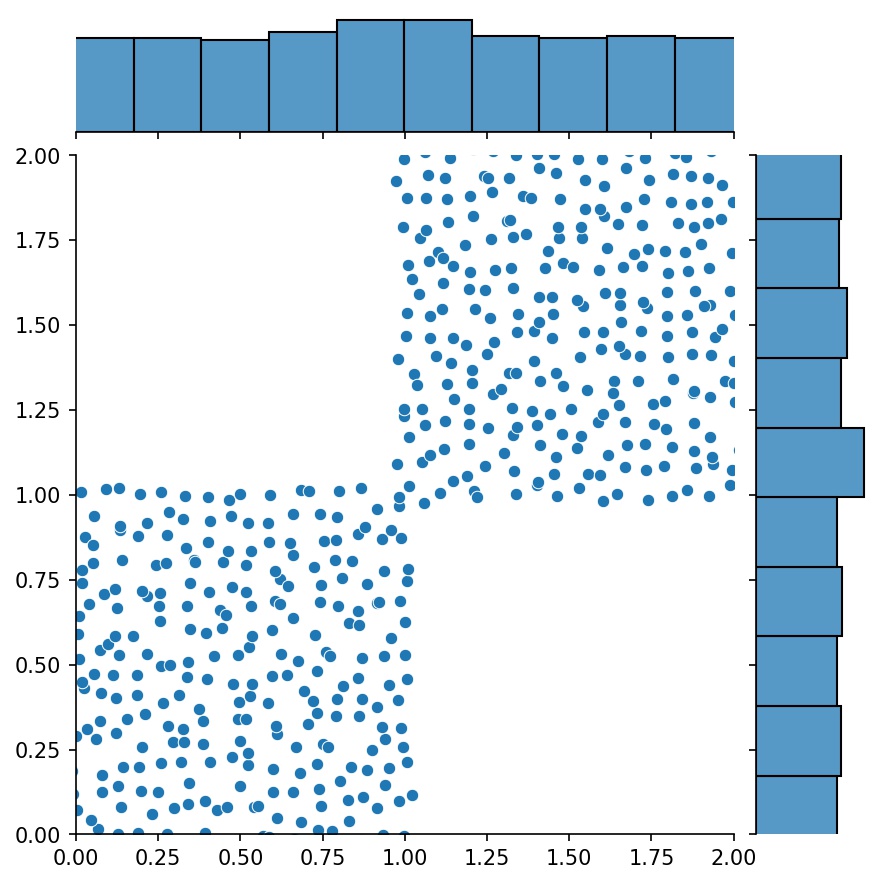 |
Vous pouvez utiliser Generator2D , Generator3D , etc. pour échantillonner des points dans des dimensions supérieures. Mais il y a aussi une autre façon
g1 = Générateur1D(1024, 2.0, 3.0, méthode='uniforme')g2 = Générateur1D(1024, 0.1, 1.0, méthode='log-spaced-noisy', noise_std=0.001)g = g1 * g2
Ici, g sera un générateur qui donne à chaque fois 1024 points dans un rectangle 2D (2,3) × (0.1,1) . Leurs coordonnées x sont tirées de (2,3) en utilisant la stratégie uniform et leur coordonnée y tirée de (0.1,1) en utilisant la stratégie log-spaced-noisy .
g1 | g2 | g1 * g2 |
|---|---|---|
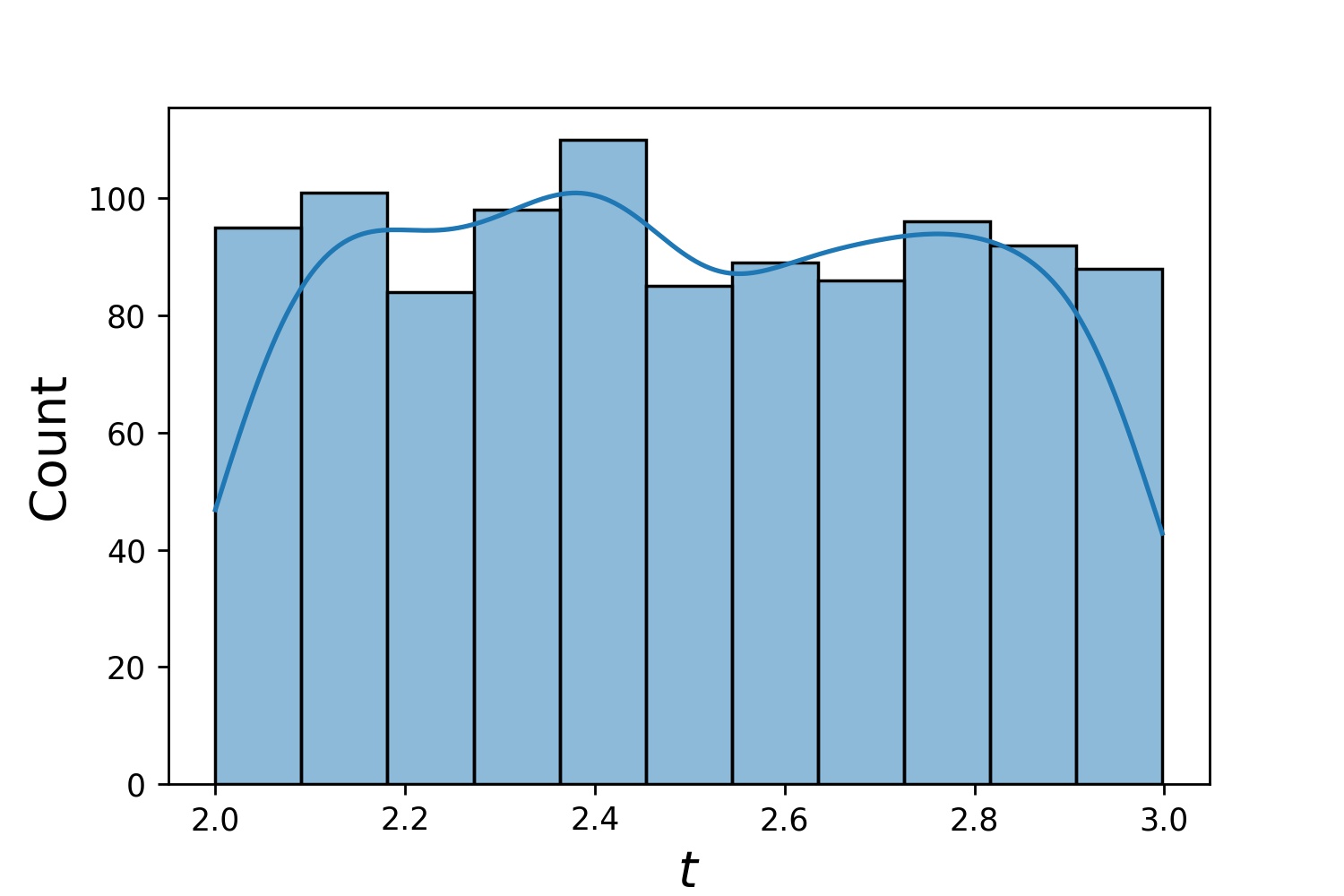 | 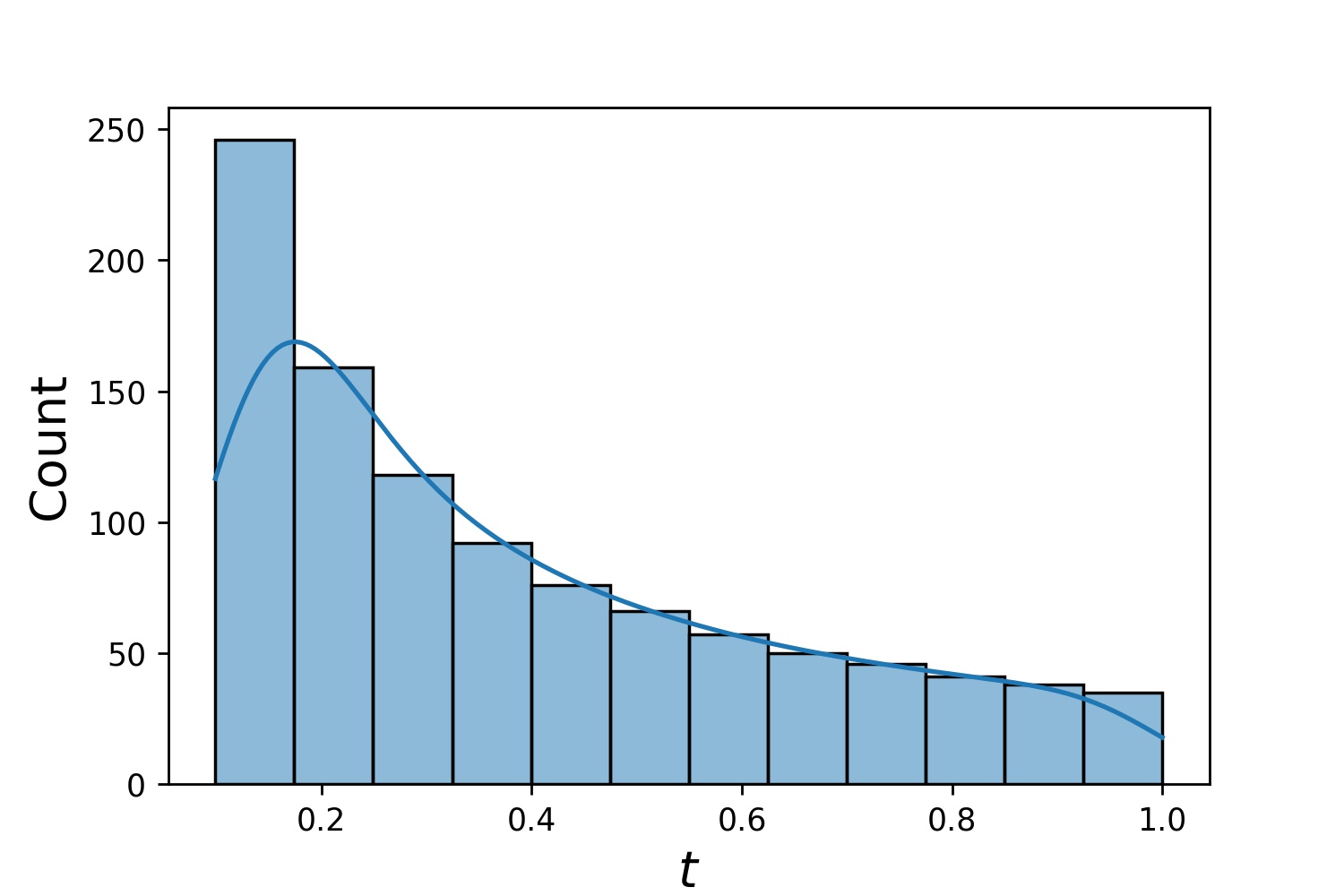 | 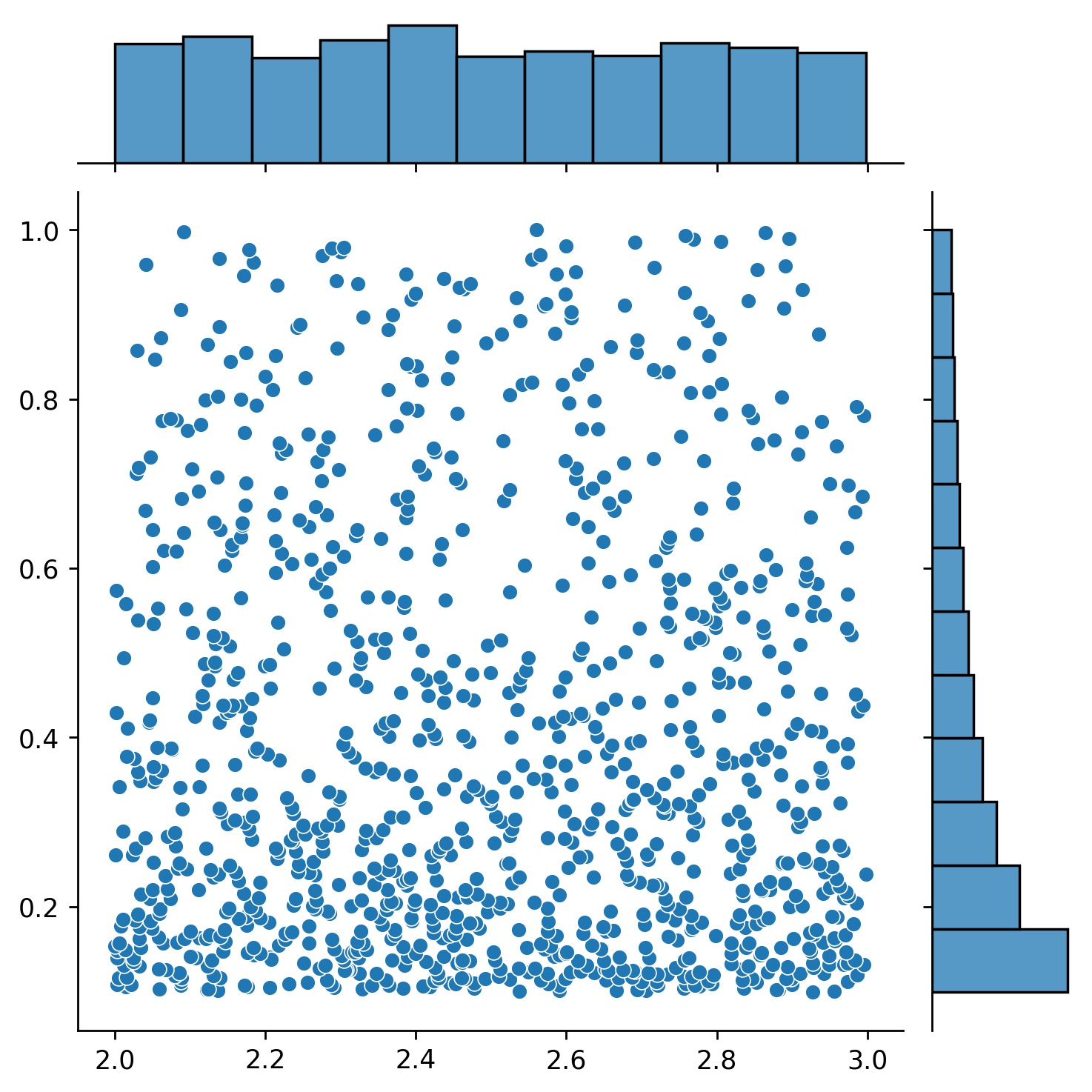 |
Parfois, il est intéressant de résoudre plusieurs équations à la fois. Par exemple, vous souhaiterez peut-être résoudre des équations différentielles de la forme du/dt + λu = 0 sous la condition initiale u(0) = U0 . Vous souhaiterez peut-être résoudre ce problème pour tous λ et U0 à la fois, en les traitant comme des entrées des réseaux de neurones.
Une de ces applications concerne les réactions chimiques, où la vitesse de réaction est inconnue. Différentes vitesses de réaction correspondent à différentes solutions, et une seule solution correspond aux points de données observés. Vous êtes peut-être intéressé par la résolution d'abord d'un ensemble de solutions, puis par la détermination des meilleurs taux de réaction (c'est-à-dire les paramètres de l'équation). La deuxième étape est connue sous le nom de problème inverse .
Voici un exemple de la façon de procéder en utilisant neurodiffeq :
Disons que nous avons une équation du/dt + λu = 0 et une condition initiale u(0) = U0 où λ et U0 sont des constantes inconnues. Nous avons également un ensemble d'observations t_obs et u_obs . Nous importons d'abord BundleSolver et BundleIVP qui sont nécessaires à l'obtention d'un bundle de solutions :
depuis neurodiffeq.conditions importer BundleIVPfrom neurodiffeq.solvers importer BundleSolver1Dimport matplotlib.pyplot en tant que pltimport numpy en tant que npimport torchfrom neurodiffeq import diff
Nous déterminons le domaine d'entrée t , ainsi que le domaine des paramètres λ et U0 . Nous devons également prendre une décision sur l’ordre des paramètres. À savoir, quel devrait être le premier paramètre et lequel devrait être le second. Pour les besoins de cette démo, nous choisissons λ comme premier paramètre (indice 0) et U0 comme deuxième (indice 1). Il est très important de garder une trace des indices des paramètres.
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # premier paramètre, index = 0U0_MIN, U0_MAX = 0,2, 0,6 # deuxième paramètre, index = 1
Nous définissons ensuite les conditions et solver comme d'habitude, sauf que nous utilisons BundleIVP et BundleSolver1D au lieu de IVP et Solver1D . L'interface de ces deux-là est très similaire à IVP et Solver1D . Vous pouvez en savoir plus dans la référence API.
# Les paramètres d'équation viennent après les entrées (généralement des coordonnées temporelles et spatiales)diff_eq = lambda u, t, lmd : [diff(u, t) + lmd * u]# L'argument mot-clé doit être nommé "u_0" dans BundleIVP. Si vous utilisez autre chose, par exemple `y0`, `u0`, etc., cela ne fonctionnera pas.conditions = [BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1}) # u_0 a index 1]solver = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ a l'index 0 ; u_0 a l'index 1theta_max=[LAMBDA_MAX, U0_MAX], # λ a l'index 0 ; paramètre d'équation, qui a l'index 0n_batches_valid=1,
) Puisque λ est un paramètre dans l'équation et U0 est un paramètre dans la condition initiale , nous devons inclure λ dans le diff_eq et U0 dans la condition. Si un paramètre est présent à la fois dans l’équation et dans la condition, il doit être inclus aux deux endroits. Tous les éléments de conditions transmis à BundleSovler1D doivent être des conditions Bundle* , même s'ils n'ont pas de paramètres.
Maintenant, nous pouvons le former et obtenir la solution comme nous le ferions normalement.
solver.fit(max_epochs=1000)solution = solver.get_solution(best=True)
La solution attend trois entrées - t , λ et U0 . Toutes les entrées doivent avoir la même forme. Par exemple, si vous souhaitez fixer λ=4 et U0=0.4 et tracer la solution u par rapport à t ∈ [0,1] , vous pouvez procéder comme suit
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0,4 * np.ones_like(t)u = solution(t, lmd, u0, to_numpy=True)importer matplotlib.pyplot en tant que pltplt .plot(t, u)
Une fois que vous disposez d'une solution groupée, vous pouvez trouver un ensemble de paramètres (λ, U0) qui correspondent le plus étroitement aux points de données observés (t_i, u_i) . Ceci est réalisé en utilisant une simple descente de gradient. Dans l'exemple de jouet suivant, nous supposons qu'il n'y a que trois points de données u(0.2) = 0.273 , u(0.5)=0.129 et u(0.8) = 0.0609 . Ce qui suit est le flux de travail PyTorch classique.
# points de données observés de λ et U0 ; garder une trace de leur gradientlmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2)# exécuter une descente de gradient pendant 10 000 époques pour _ dans la plage (10 000) : sortie = solution (t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs))loss = ((sortie - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, perte = {loss.item()}") Simple. Lors de l'importation de neurodiffeq, la bibliothèque détecte automatiquement si CUDA est disponible sur votre machine. Étant donné que la bibliothèque est basée sur PyTorch, elle définira le type de tenseur par défaut sur torch.cuda.DoubleTensor si un périphérique GPU compatible est trouvé.
Reportez-vous aux sections Réseaux personnalisés et Apprentissage par transfert.
La méthode standard de PyTorch.
Construisez vos réseaux comme expliqué dans Réseaux personnalisés : nets = [FCNN(), FCN(), ...]
Instancier un optimiseur personnalisé et lui transmettre tous les paramètres de ces réseaux
settings = [p for net in nets for p in net.parameters()] # liste des paramètres de tous les réseauxMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
Passez vos DEUX nets et votre optimizer au solveur : solver = Solver1D(..., nets=nets, optimizer=optimizer)
Contrairement aux méthodes numériques traditionnelles (FEM, FVM, etc.), la solution basée sur NN nécessite un certain hyperréglage. La bibliothèque offre la plus grande flexibilité pour essayer n'importe quelle combinaison d'hyperparamètres.
Pour utiliser une architecture réseau différente, vous pouvez transmettre vos torch.nn.Module personnalisés.
Pour utiliser un autre optimiseur, vous pouvez transmettre votre propre optimiseur à solver = Solver(..., optimizer=my_optim) .
Pour utiliser une distribution d'échantillonnage différente, vous pouvez utiliser des générateurs intégrés ou écrire vos propres générateurs à partir de zéro.
Pour utiliser une taille d'échantillonnage différente, vous pouvez modifier les générateurs ou modifier solver = Solver(..., n_batches_train) .
Pour modifier dynamiquement les hyperparamètres pendant l'entraînement, consultez notre fonctionnalité de rappels.
N'utilisez pas ReLU pour l'activation, car sa dérivée du second ordre est identique à 0.
Redimensionnez votre PDE/ODE sous forme sans dimension, de préférence en faisant en sorte que tout se situe dans [0,1] . Travailler avec un domaine comme [0,1000000] est sujet à l'échec car a) PyTorch initialise les poids des modules pour qu'ils soient relativement petits et b) la plupart des fonctions d'activation (comme Sigmoid, Tanh, Swish) sont les plus non linéaires proches de 0.
Si votre PDE/ODE est trop compliqué, envisagez d’essayer l’apprentissage du programme. Commencez à former vos réseaux sur un domaine plus petit, puis développez-le progressivement jusqu'à ce que l'ensemble du domaine soit couvert.
Tout le monde est invité à contribuer à ce projet.
Lorsque nous contribuons à ce référentiel, nous considérons le processus suivant :
Ouvrez un problème pour discuter du changement que vous envisagez d'apporter.
Parcourez les directives de contribution.
Effectuez la modification sur un référentiel forké et mettez à jour le fichier README.md si des modifications sont apportées à l'interface.
Ouvrez une pull request.