ai simplest network

Réseau de neurones artificiels le plus simple

Il s’agit du réseau neuronal artificiel le plus simple possible, expliqué et démontré.

Ceci est la première partie d'une série de dépôts github sur les réseaux de neurones

• partie 1 - réseau le plus simple ( vous êtes ici )
• partie 2 - rétropropagation
• partie 3 - rétropropagation-suite

Table des matières

• Théorie
  • Imiter les neurones
  • Un exemple simple
  • L'erreur
  • Descente de gradient
• Exemple de code
• Références

Théorie

Imiter les neurones

Les réseaux de neurones artificiels s'inspirent du cerveau en permettant aux neurones artificiels interconnectés de stocker des modèles et de communiquer entre eux. La forme la plus simple d'un neurone artificiel possède une ou plusieurs entrées chacun ayant un poids spécifique et une sortie .

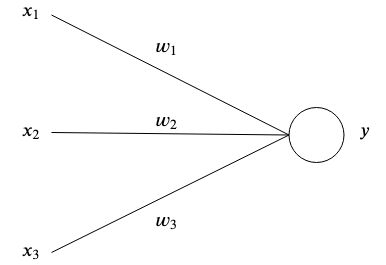
Au niveau le plus simple, le résultat est la somme de ses entrées multipliée par ses poids.

Un exemple simple

Le but d'un réseau est d'apprendre un certain résultat compte tenu de certaines entrées en approximant une fonction complexe avec de nombreux paramètres que nous ne pouvions pas inventer nous-mêmes.

Disons que nous avons un réseau avec deux entrées et et deux poids et .

L’idée est d’ajuster les pondérations de telle manière que les intrants donnés produisent le résultat souhaité.

Les poids sont normalement initialisés de manière aléatoire puisque nous ne pouvons pas connaître leur valeur optimale à l'avance. Cependant, pour des raisons de simplicité, nous les initialiserons tous les deux à .

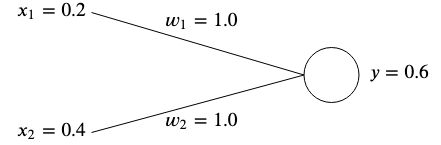
Si nous calculons la sortie de ce réseau, nous obtiendrons

L'erreur

Si la sortie ne correspond pas à la valeur cible attendue, alors nous avons une erreur.
Par exemple, si nous voulions obtenir une valeur cible de alors nous aurions une différence de

Une façon courante de mesurer l’erreur (également appelée fonction de coût) consiste à utiliser l’erreur quadratique moyenne :

Si nous avions plusieurs associations d'entrées et de valeurs cibles, alors l'erreur devient la somme moyenne de chaque association.

Nous utilisons l'erreur quadratique moyenne pour mesurer la distance entre les résultats et notre cible souhaitée. La mise au carré supprime les signes négatifs et donne plus de poids aux différences plus importantes entre le résultat et l’objectif.

Pour rectifier l'erreur, nous devrons ajuster les pondérations de manière à ce que le résultat corresponde à notre objectif. Dans notre exemple, baisser depuis à ferait l'affaire, puisque

Cependant, afin d'ajuster les poids de nos réseaux neuronaux pour de nombreuses entrées et valeurs cibles différentes, nous avons besoin d'un algorithme d'apprentissage pour le faire automatiquement pour nous.

Descente de gradient

L'idée est d'utiliser l'erreur pour comprendre comment chaque poids doit être ajusté afin que l'erreur soit minimisée, mais nous devons d'abord nous renseigner sur les gradients.

Qu'est-ce qu'un dégradé ?

Il s'agit essentiellement d'un vecteur indiquant la direction de la montée la plus raide d'une fonction. Le dégradé est noté par et est simplement la dérivée partielle de chaque variable d'une fonction exprimée sous forme de vecteur.

Cela ressemble à ceci pour une fonction à deux variables :

Injectons quelques nombres et calculons le dégradé avec un exemple simple. Disons que nous avons une fonction , alors le dégradé serait

Qu’est-ce que la descente de gradient ?

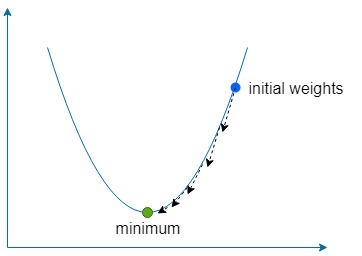
La partie descente signifie simplement utiliser la pente pour trouver la direction de montée la plus raide de notre fonction, puis aller plusieurs fois dans la direction opposée pour trouver le minimum global (ou parfois local) de la fonction.

Nous utilisons une constante appelée taux d'apprentissage , notée pour définir le petit pas à faire dans cette direction.

Si est trop grand, alors nous risquons de dépasser le minimum de la fonction, mais s'il est trop faible, le réseau mettra plus de temps à apprendre et nous risquons de rester bloqués dans un minimum local peu profond.

Descente de gradient appliquée à notre exemple de réseau

Pour nos deux poids et nous devons trouver le gradient de ces poids par rapport à la fonction d'erreur

Pour les deux et , nous pouvons trouver le dégradé en utilisant la règle de chaîne

Nous désignerons désormais le comme le terme pour la simplicité.

Une fois que nous avons le gradient, nous pouvons mettre à jour nos poids en soustrayant le gradient calculé multiplié par le taux d'apprentissage.

Et nous répétons ce processus jusqu'à ce que l'erreur soit minimisée et suffisamment proche de zéro.

Exemple de code

L'exemple inclus enseigne l'ensemble de données suivant à un réseau de neurones avec deux entrées et une sortie utilisant la descente de gradient :

Une fois appris, le réseau devrait afficher ~ 0 lorsqu'on lui donne deux s et ~ lorsqu'on lui donne un et un .

Comment courir

En ligne sur repl.it

Docker

docker build -t simplest-network .
docker run --rm simplest-network

Références

1. Moteurs d'intelligence artificielle de James V Stone (2019)
2. Guide complet sur le deep learning : http://neuralnetworksanddeeplearning.com/chap2.html