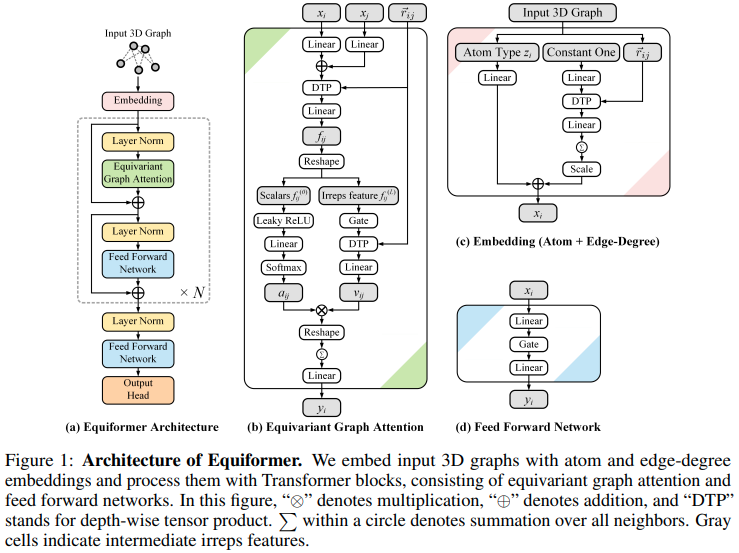
equiformer pytorch Télécharger - equiformer pytorch Téléchargement du code source

Equiformer - Pytorch (wip)

Implémentation du réseau d'attention équivariant Equiformer, SE3/E3 qui atteint le nouveau SOTA et adopté pour utilisation par EquiFold (Prescient Design) pour le repliement des protéines

La conception de celui-ci semble s'appuyer sur les transformateurs SE3, l'attention du produit scalaire étant remplacée par l'attention MLP et le message non linéaire transmis par GATv2. Il effectue également un produit tenseur en profondeur pour un peu plus d'efficacité. Si vous pensez que je me trompe, n'hésitez pas à m'envoyer un e-mail.

Mise à jour : il y a eu un nouveau développement qui améliore considérablement la mise à l'échelle du nombre de degrés pour les réseaux équivariants SE3 ! Cet article a d'abord noté qu'en alignant les représentations le long de l'axe z (ou de l'axe y par une autre convention), les harmoniques sphériques deviennent clairsemées. Cela supprime la dimension m _f de l'équation. Un article de suivi de Passaro et al. a noté que la matrice de Clebsch Gordan est également devenue clairsemée, conduisant à la suppression de m _i et l _f . Ils ont également fait le lien selon lequel le problème a été réduit de SO(3) à SO(2) après avoir aligné les répétitions sur un axe. Equiformer v2 (dépôt officiel) exploite cela dans un cadre de type transformateur pour atteindre un nouveau SOTA.

J'y consacrerai certainement plus de travail/d'exploration. Pour l'instant, j'ai incorporé les astuces des deux premiers articles pour Equiformer v1, à l'exception de la conversion complète en SO(2).

Mise à jour 2 : il semble y avoir un nouveau SOTA sans aucune interaction entre les représentants de degré supérieur (en d'autres termes, tous les produits tensoriels/clebsch gordan mathématiques disparaissent). GotenNet, qui semble être une interprétation par transformateur de HEGNN

Installer

$ pip install equiformer-pytorch

Usage

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),               # dimensions per type, ascending, length must match number of degrees (num_degrees)
    dim_head = ( 4 , 4 , 4 ),          # dimension per attention head
    heads = ( 2 , 2 , 2 ),             # number of attention heads
    num_linear_attn_heads = 0 ,     # number of global linear attention heads, can see all the neighbors
    num_degrees = 3 ,               # number of degrees
    depth = 4 ,                     # depth of equivariant transformer
    attend_self = True ,            # attending to self or not
    reduce_dim_out = True ,         # whether to reduce out to dimension of 1, say for predicting new coordinates for type 1 features
    l2_dist_attention = False      # set to False to try out MLP attention
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask ) # (1, 128)

out . type0 # invariant type 0    - (1, 128)
out . type1 # equivariant type 1  - (1, 128, 3)

Ce référentiel comprend également un moyen de découpler l'utilisation de la mémoire de la profondeur à l'aide de réseaux réversibles. En d'autres termes, si vous augmentez la profondeur, le coût de la mémoire restera constant lors de l'utilisation d'un bloc transformateur équiformateur (attention et feedforward).

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),
    dim_head = ( 4 , 4 , 4 ),
    heads = ( 2 , 2 , 2 ),
    num_degrees = 3 ,
    depth = 48 ,          # depth of 48 - just to show that it runs - in reality, seems to be quite unstable at higher depths, so architecture stil needs more work
    reversible = True ,   # just set this to True to use https://arxiv.org/abs/1707.04585
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask )

out . type0 . sum (). backward ()

Bords

avec des bords, ex. liaisons atomiques

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

out = model ( atoms , coors , mask , edges = bonds )

out . type0 # (2, 32)
out . type1 # (2, 32, 3)

avec matrice de contiguïté

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    reduce_dim_out = True ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    num_adj_degrees_embed = 2 ,       # this will derive the second degree connections and embed it correctly
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat )

out . type0 # (1, 128)
out . type1 # (1, 128, 3)

Appréciation

StabilityAI pour son généreux parrainage, ainsi que mes autres sponsors

Essai

Tests d'équivariance, etc.

$ python setup.py test

Exemple

Installez d’abord sidechainnet

$ pip install sidechainnet

Ensuite, exécutez la tâche de débruitage du squelette protéique

$ python denoise.py

Faire

Citations

 @article { Liao2022EquiformerEG ,
    title   = { Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs } ,
    author  = { Yi Liao and Tess E. Smidt } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.11990 }
}

 @article { Lee2022.10.07.511322 ,
    author  = { Lee, Jae Hyeon and Yadollahpour, Payman and Watkins, Andrew and Frey, Nathan C. and Leaver-Fay, Andrew and Ra, Stephen and Cho, Kyunghyun and Gligorijevic, Vladimir and Regev, Aviv and Bonneau, Richard } ,
    title   = { EquiFold: Protein Structure Prediction with a Novel Coarse-Grained Structure Representation } ,
    elocation-id = { 2022.10.07.511322 } ,
    year    = { 2022 } ,
    doi     = { 10.1101/2022.10.07.511322 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322 } ,
    eprint  = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Shazeer2019FastTD ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam M. Shazeer } ,
    journal = { ArXiv } ,
    year    = { 2019 } ,
    volume  = { abs/1911.02150 }
}

 @misc { ding2021cogview ,
    title   = { CogView: Mastering Text-to-Image Generation via Transformers } ,
    author  = { Ming Ding and Zhuoyi Yang and Wenyi Hong and Wendi Zheng and Chang Zhou and Da Yin and Junyang Lin and Xu Zou and Zhou Shao and Hongxia Yang and Jie Tang } ,
    year    = { 2021 } ,
    eprint  = { 2105.13290 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @inproceedings { Kim2020TheLC ,
    title   = { The Lipschitz Constant of Self-Attention } ,
    author  = { Hyunjik Kim and George Papamakarios and Andriy Mnih } ,
    booktitle = { International Conference on Machine Learning } ,
    year    = { 2020 }
}

 @article { Zitnick2022SphericalCF ,
    title   = { Spherical Channels for Modeling Atomic Interactions } ,
    author  = { C. Lawrence Zitnick and Abhishek Das and Adeesh Kolluru and Janice Lan and Muhammed Shuaibi and Anuroop Sriram and Zachary W. Ulissi and Brandon C. Wood } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.14331 }
}

 @article { Passaro2023ReducingSC ,
  title     = { Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs } ,
  author    = { Saro Passaro and C. Lawrence Zitnick } ,
  journal   = { ArXiv } ,
  year      = { 2023 } ,
  volume    = { abs/2302.03655 }
}

 @inproceedings { Gomez2017TheRR ,
    title   = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author  = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger Baker Grosse } ,
    booktitle = { NIPS } ,
    year    = { 2017 }
}

 @article { Bondarenko2023QuantizableTR ,
    title   = { Quantizable Transformers: Removing Outliers by Helping Attention Heads Do Nothing } ,
    author  = { Yelysei Bondarenko and Markus Nagel and Tijmen Blankevoort } ,
    journal = { ArXiv } ,
    year    = { 2023 } ,
    volume  = { abs/2306.12929 } ,
    url     = { https://api.semanticscholar.org/CorpusID:259224568 }
}

 @inproceedings { Arora2023ZoologyMA ,
  title   = { Zoology: Measuring and Improving Recall in Efficient Language Models } ,
  author  = { Simran Arora and Sabri Eyuboglu and Aman Timalsina and Isys Johnson and Michael Poli and James Zou and Atri Rudra and Christopher R'e } ,
  year    = { 2023 } ,
  url     = { https://api.semanticscholar.org/CorpusID:266149332 }
}