Une implémentation de l'algorithme Minimax AI sur le jeu Tic-Tac-Toe (ou Noughts and Crosses). Essayez-le : Tic-tac-toe - Minimax
Pour résoudre des jeux utilisant l’IA, nous présenterons le concept d’arbre de jeu suivi de l’algorithme minimax. Les différents états du jeu sont représentés par des nœuds dans l’arbre du jeu, très similaires aux problèmes de planification ci-dessus. L'idée est juste légèrement différente. Dans l'arbre de jeu, les nœuds sont disposés en niveaux qui correspondent aux tours de chaque joueur dans le jeu de sorte que le nœud « racine » de l'arbre (généralement représenté en haut du diagramme) soit la position de début du jeu. Au tic-tac-toe, ce serait la grille vide sans X ni Os encore joués. Sous racine, au deuxième niveau, se trouvent les états possibles qui peuvent résulter des mouvements du premier joueur, que ce soit X ou O. Nous appelons ces nœuds les « enfants » du nœud racine.
Chaque nœud du deuxième niveau aurait en outre comme nœuds enfants les états qui peuvent être atteints à partir de lui par les mouvements du joueur adverse. Ceci se poursuit, niveau par niveau, jusqu'à atteindre les états où le jeu est terminé. Au tic-tac-toe, cela signifie que soit l'un des joueurs obtient une ligne de trois et gagne, soit le plateau est plein et la partie se termine par une égalité.
Minimax est une intelligence artificielle appliquée aux jeux à deux joueurs, tels que le tic-tac-toe, les dames, les échecs et le go. Ces jeux sont connus sous le nom de jeux à somme nulle, car dans une représentation mathématique : un joueur gagne (+1) et l'autre joueur perd (-1) ou les deux ne gagnent pas (0).
L'algorithme recherche, de manière récursive, le meilleur coup qui amène le joueur Max à gagner ou à ne pas perdre (match nul). Il considère l'état actuel du jeu et les coups disponibles à cet état, puis pour chaque coup valide, il joue (en alternant min et max ) jusqu'à ce qu'il trouve un état terminal (gagner, nul ou perdre).
L'algorithme a été étudié dans le livre Algorithms in a Nutshell (George Heineman ; Gary Pollice ; Stanley Selkow, 2009). Pseudocode (adapté) :
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
Nous allons maintenant voir chaque partie de ce pseudocode avec l'implémentation Python. L'implémentation Python est disponible sur ce référentiel. Tout d’abord, considérez ceci :
tableau = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
MAX = +1
MINIMUM = -1
Le MAX peut être X ou O et le MIN peut être O ou X, peu importe. Le plateau est 3x3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]Les deux joueurs commencent avec votre pire score. Si le joueur est MAX, son score est -infini. Sinon, si le joueur est MIN, son score est +infini. Remarque : infinity est un alias pour inf (du module mathématique, en Python).
Le meilleur coup sur le plateau est [-1, -1] (ligne et colonne) pour tous.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreSi la profondeur est égale à zéro, alors le plateau n'a pas de nouvelles cellules vides à jouer. Ou, si un joueur gagne, alors le jeu se termine pour MAX ou MIN. Le score de cet état sera donc renvoyé.
Nous allons maintenant voir la partie principale de ce code qui contient la récursion.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yPour chaque coup valide (cellules vides) :
Le mouvement (+1 ou -1) sur le plateau est annulé et la ligne et la colonne sont collectées.
L'étape suivante consiste à comparer le score avec le meilleur.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scorePour le joueur MAX, un score plus élevé sera reçu. Pour un joueur MIN, un score inférieur sera obtenu. Et à la fin, le meilleur coup est rendu. Algorithme final :
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best Ci-dessous, le meilleur coup est au milieu car la valeur maximale est sur le 2ème nœud à gauche.
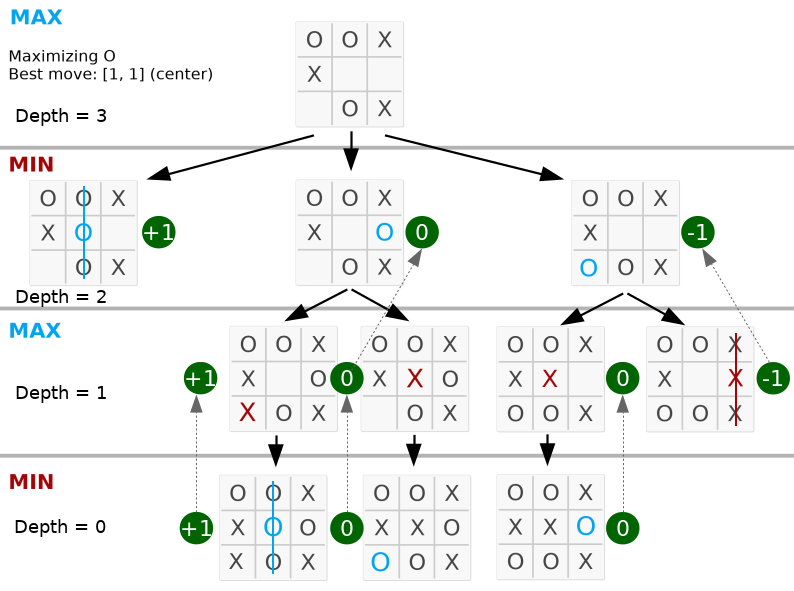
Vérifiez que la profondeur est égale aux mouvements valides sur le plateau. Le code complet est disponible dans py_version/ .
Arbre de jeu simplifié :
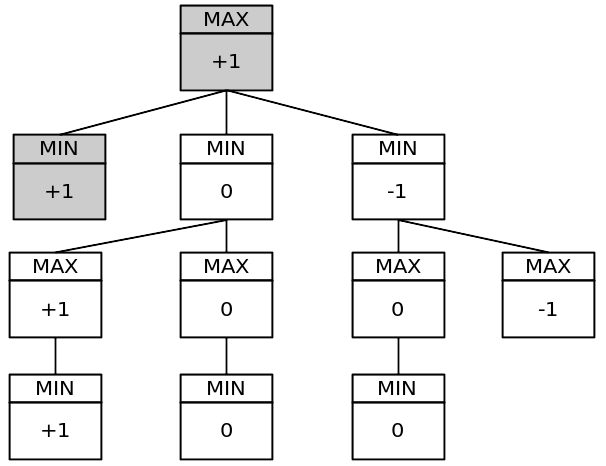
Cet arbre a 11 nœuds. L'arbre de jeu complet compte 549 946 nœuds ! Vous pouvez le tester en mettant une variable globale statique dans votre programme et en l'incrémentant pour chaque appel de fonction minimax par tour.
Dans un jeu plus complexe, comme les échecs, il est difficile de parcourir l'ensemble de l'arbre du jeu. Cependant, Alpha-beta Pruning est une méthode d'optimisation de l'algorithme minimax qui nous permet d'ignorer certaines branches de l'arbre de recherche, car il coupe les nœuds (sous-arbres) non pertinents dans la recherche. Pour plus d'informations, voir :