
Le présentateur d'équipe: Kahraman Kostas
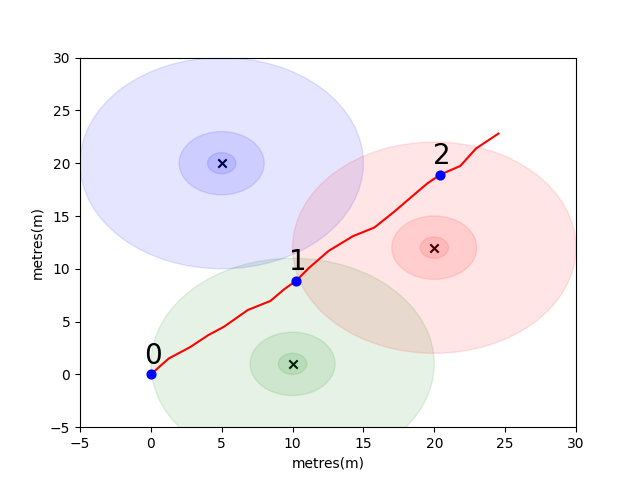
Pour commencer, nous avons mis en place un problème simple pour introduire certains concepts clés de positionnement intérieur. Considérez l'environnement suivant: Un utilisateur voyage dans un espace ouvert en présence de 3 émetteurs WiFi (nous appelons les données créées par cet utilisateur une trajectoire). Chaque émetteur a une adresse MAC unique. L'utilisateur est équipé d'un smartphone qui scannera périodiquement l'environnement WiFi et enregistrera le RSSI de chaque Mac détecté (en dB).
Pour ce modèle, nous avons utilisé un modèle de propagation standard sur la perte de bogue pour chacun des émetteurs. Il s'agit d'un modèle simpliste qui fonctionne bien dans l'espace libre, mais se décompose dans des environnements intérieurs réels avec des murs et d'autres obstacles qui peuvent faire rebondir les signaux de manière plus complexe. En général, nous nous attendons à voir une baisse abrupte de RSSI sur la distance car l'énergie fixe de l'antenne émettrice est répartie sur une zone croissante à mesure que l'onde se propage. Dans le diagramme en dessous de chaque cercle, une goutte de 10 dB.
L'utilisateur se promène au nord-est à partir du point (0,0) et le téléphone fait trois scans de l'environnement. Les données enregistrées à chaque scan sont présentées ci-dessous.
scan 0 -> {'green': -60, 'blue': -66, 'red': -67}
scan 1 -> {'green': -58, 'blue': -61, 'red': -60}
scan 2 -> {'green': -66, 'blue': -62, 'red': -59}
Les propriétés complexes et localement uniques de l'environnement WiFi le rendent très utile pour les systèmes de positionnement intérieur. Par exemple, dans l'image ci-dessous, scan 1 mesure les données à peu près au centre de centroïde des trois émetteurs et il n'y a pas d'autre endroit dans cet environnement où l'on pourrait prendre une lecture qui enregistrerait des valeurs RSSI similaires. Compte tenu d'un ensemble de scans ou de "empreintes digitales" à partir de trajectoires indépendantes, nous sommes intéressés à calculer à quel point ils sont similaires dans l'espace WiFi car il s'agit d'une indication de leur proximité dans l'espace réel.
Votre premier défi est d'écrire une fonction pour calculer la distance euclidienne et les mesures de distance de Manhattan entre chacun des analyses de la trajectoire de l'échantillon que nous avons introduit ci-dessus. L'utilisation des données d'une seule trajectoire est un bon moyen de tester la qualité d'une métrique de similitude car nous pouvons obtenir des estimations assez précises de la distance réelle en utilisant les données de l'unité de mesure intertiale du téléphone (IMU) qui est utilisée par un calcul mort piétonne (PDR) Module.
def euclidean ( fp1 , fp2 ):
raise NotImplementedError
def manhattan ( fp1 , fp2 ):
raise NotImplementedError # solution of the above functions
from scipy . spatial import distance
def euclidean ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . euclidean ( fp1 , fp2 )
def manhattan ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . cityblock ( fp1 , fp2 ) import json
import numpy as np
import matplotlib . pyplot as plt
from metrics import eval_dist_metric
with open ( "intro_trajectory_1.json" ) as f :
traj = json . load ( f )
## Pre-calculate the pair indexes we are interested in
keys = []
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
# only calculate the upper triangle
if fp1 [ 'step_index' ] > fp2 [ 'step_index' ]:
keys . append (( fp1 [ 'step_index' ], fp2 [ 'step_index' ]))
## Get the distances from PDR
true_d = {}
for step1 in traj [ 'steps' ]:
for step2 in traj [ 'steps' ]:
key = ( step1 [ 'step_index' ], step2 [ 'step_index' ])
if key in keys :
true_d [ key ] = abs ( step1 [ 'di' ] - step2 [ 'di' ])
euc_d = {}
man_d = {}
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
key = ( fp1 [ 'step_index' ], fp2 [ 'step_index' ])
if key in keys :
euc_d [ key ] = euclidean ( fp1 [ 'profile' ], fp2 [ 'profile' ])
man_d [ key ] = manhattan ( fp1 [ 'profile' ], fp2 [ 'profile' ])
print ( "Euclidean Average Error" )
print ( f' { eval_dist_metric ( euc_d , true_d ):.2f } ' )
print ( "Manhattan Average Error" )
print ( f' { eval_dist_metric ( man_d , true_d ):.2f } ' ) Euclidean Average Error
9.29
Manhattan Average Error
4.90
Si vous avez correctement implémenté les fonctions, vous auriez dû voir que l'erreur moyenne pour la métrique euclidienne était 9.29 tandis que le Manhattan n'était que 4.90 . Ainsi, pour ces données, la distance de Manhattan est une meilleure estimation de la vraie distance.
C'est bien sûr un modèle très simpliste. En effet, il n'y a pas de relation directe entre les valeurs RSSI et la distance d'espace libre de cette manière. En règle générale, lorsque nous créons nos propres estimations pour la distance, nous utiliserions les distances connues de PDR à l'intérieur d'une trajectoire pour s'adapter au score numérique à une estimation de distance physique.
Pour votre principal défi, nous aimerions que vous développiez votre propre métrique pour estimer la distance réelle entre deux analyses, basées uniquement sur leurs empreintes digitales WiFi. Nous vous fournirons de véritables données de crowdsourced collectées au début de 2021 dans un seul centre commercial. Les données contiendront les analyses d'empreintes digitales 114661 et 879824 distances entre les analyses. Les distances seront notre meilleure estimation de la véritable distance donnée par les informations supplémentaires que nous prendrons en compte.
Nous fournirons un ensemble de tests de paires d'empreintes digitales et vous devrez écrire une fonction qui nous indique à quelle distance elles sont.
Cette fonction pourrait être aussi simple qu'une variation de l'une des mesures que nous avons introduites ci-dessus ou aussi complexes qu'une solution d'apprentissage automatique complète qui apprend à pondérer différentes adresses MAC (ou combinaisons d'adresses MAC) différemment dans différentes situations.
Quelques points finaux à considérer:
Les données sont assemblées en trois fichiers pour vous.
La task1_fingerprints.json contient toutes les informations d'empreinte digitale pour le problème. C'est-à-dire que chaque entrée représente un véritable scan des émetteurs WiFi dans une zone du centre commercial. Vous constaterez que les mêmes adresses MAC seront présentes dans de nombreuses empreintes digitales.
La task1_train.csv contient les paires de formation valides pour vous aider à concevoir / former votre algorithme. Chaque paire id1-id2 a une distance de vérité au sol étiquetée (en mètres) et chaque ID correspond à des empreintes digitales de task1_fingerprints.json .
La task1_test.csv est le même format que task1_train.csv mais n'a pas les déplacements inclus. Ce sont ce que nous aimerions que vous prédiriez en utilisant les informations brutes d'empreintes digitales.
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
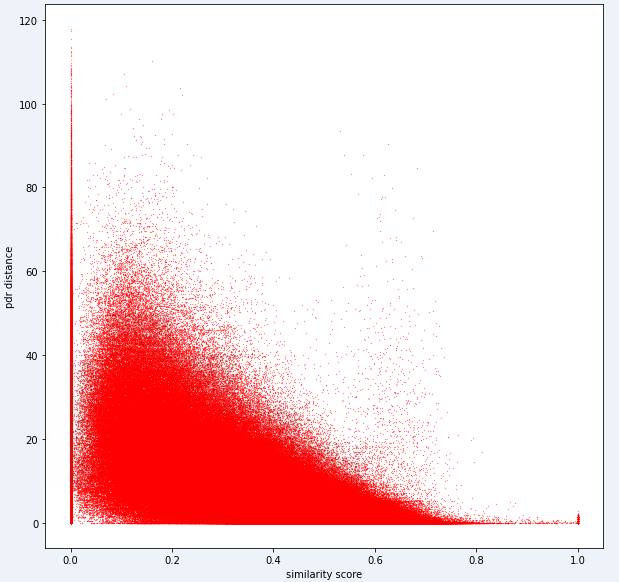
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]])En fin de compte, le modèle idéal devrait être capable de trouver une cartographie exacte entre l'espace d'empreintes digitales hautement dimensionnel (1 empreinte digitale peut contenir de nombreuses mesures) et l'espace de distance 1 dimensionnel. Il peut être utile de tracer la distance PDR (des données de formation) contre une métrique de similitude calculée pour voir si la métrique révèle une tendance évidente. Une similitude élevée devrait être en corrélation avec une faible distance.
Vous trouverez ci-dessous une métrique de distance que nous utilisons en interne pour cette tâche. Vous pouvez voir que même pour cette métrique, nous avons une quantité considérable de bruit.
En raison de ce niveau de bruit, notre métrique de notation pour la tâche 1 sera biaisée vers la précision sur le rappel
Votre soumission doit utiliser les ID exacts du fichier test1_test.csv et doit remplir la troisième colonne de déplacement (actuellement vide) avec votre distance estimée (en mètres) pour cette paire d'empreintes digitales.
def my_distance_function ( fp1 , fp2 ):
raise NotImplementedError output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
fp1 = fps [ id1 ]
fp2 = fps [ id2 ]
distance_estimate = my_distance_function ( fp1 , fp2 )
output_data . append ([ id1 , id2 , distance_estimate ])
with open ( "MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )Les étapes de la première tâche peuvent être résumées comme suit.
Ces étapes sont illustrées dans l'image ci-dessous.

Nous avons utilisé Python 3.6.5 pour créer le fichier d'application. Nous avons inclus des modules supplémentaires qui n'ont pas été inclus dans l'exemple de fichier donné au début de la compétition. Ces modules peuvent être répertoriés comme:
| Molules | Tâche |
|---|---|
| tensorflow | Apprentissage en profondeur |
| Pandas | Analyse des données |
| Cavalier | Informatique à distance |
Nous avons commencé avec l'installation de ces modules comme première étape.
## 1.1 Installing modules
!p ip install tensorflow == 2.6 . 2
!p ip install scipy
!p ip install pandas Dans cette étape, nous avons corrigé la graine aléatoire associée à utiliser afin d'obtenir des résultats reproductibles. De cette façon, nous avons fourni un chemin déterministe où nous obtenons le même résultat à chaque cycle. Cependant, selon nos observations, les résultats obtenus avec différents ordinateurs peuvent différer légèrement (± 1%)
## 1.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )
import tensorflow as tf
tf . random . set_seed ( seed_value )
import tensorflow as tf
session_conf = tf . compat . v1 . ConfigProto ( intra_op_parallelism_threads = 1 , inter_op_parallelism_threads = 1 )
sess = tf . compat . v1 . Session ( graph = tf . compat . v1 . get_default_graph (), config = session_conf ) Dans cette section, nous chargeons les données que nous utiliserons. Nous avons pris le code et les explications à partir de l'exemple de fichier donné ( Task1-IPS-Challenge-2021.ipynb ).
La task1_fingerprints.json contient toutes les informations d'empreinte digitale pour le problème. C'est-à-dire que chaque entrée représente un véritable scan des émetteurs WiFi dans une zone du centre commercial. Vous constaterez que les mêmes adresses MAC seront présentes dans de nombreuses empreintes digitales.
La task1_train.csv contient les paires de formation valides pour vous aider à concevoir / former votre algorithme. Chaque paire id1-id2 a une distance de vérité au sol étiquetée (en mètres) et chaque ID correspond à des empreintes digitales de task1_fingerprints.json .
La task1_test.csv est le même format que task1_train.csv mais n'a pas les déplacements inclus.
## 1.3 Loading the data
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]]) 879824it [05:16, 2778.31it/s]
5160445it [01:00, 85269.27it/s]
Dans cette étape, nous effectuons l'extraction des fonctionnalités en utilisant deux fonctions. feature_extraction_file La fonction tire simplement les valeurs pertinentes des empreintes digitales (en paires) du fichier JSON et les envoie à la fonction feature_extraction pour faire les calculs.
Dans la fonction feature_extraction , si ces deux empreintes digitales sont différentes les unes des autres en termes de taille et les appareils qu'ils contiennent, tous les appareils inclus dans les deux empreintes digitales sont réunies pour former une séquence commune sans répéter. Dans chaque tableau, nous rendons ces deux tableaux identiques (en termes de dispositifs qu'ils incluent) en attribuant la valeur 0 aux dispositifs non correcteurs. Ce processus est expliqué avec un exemple dans l'image suivante.
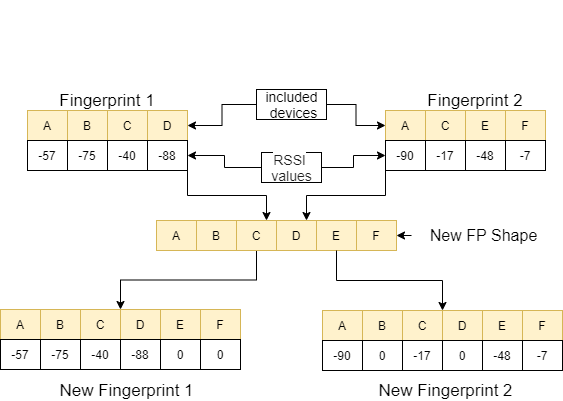
La distance entre ces deux empreintes digitales, qui sont fabriquées similaires, est calculée en utilisant 11 méthodes différentes [1]. Ces méthodes sont:
Ensuite, ces valeurs sont dirigées vers la fonction feature_extraction_file et enregistrées en tant que fichier CSV dans cette fonction. En d'autres termes, les empreintes digitales de différentes tailles se transforment en un fichier CSV à 11 fonctionnalités à la suite de ce processus. Le modèle à utiliser est formé et testé avec ces fonctionnalités nouvellement créées.
## 1.4 Feature Extraction
def feature_extraction_file ( data , name , flag ):
features = [[ "braycurtis" ,
"canberra" ,
"chebyshev" ,
"cityblock" ,
"correlation" ,
"cosine" ,
"euclidean" ,
"jensenshannon" ,
"minkowski" ,
"sqeuclidean" ,
"wminkowski" , "real" ]]
for i in tqdm (( data ), position = 0 , leave = True ):
fp1 = fps [ i [ 0 ]]
fp2 = fps [ i [ 1 ]]
feature = feature_extraction ( fp1 , fp2 )
if flag :
feature . append ( i [ 2 ])
else : feature . append ( 0 )
features . append ( feature )
with open ( name , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( features )
#print(features) ## 1.4 Feature Extraction
def feature_extraction ( fp1 , fp2 ):
mac = set ( list ( fp1 . keys ()) + list ( fp2 . keys ()))
mac = { i : 0 for i in mac }
f1 = mac . copy ()
f2 = mac . copy ()
for key in fp1 :
f1 [ key ] = fp1 [ key ]
for key in fp2 :
f2 [ key ] = fp2 [ key ]
f1 = list ( f1 . values ())
f2 = list ( f2 . values ())
braycurtis = scipy . spatial . distance . braycurtis ( f1 , f2 )
canberra = scipy . spatial . distance . canberra ( f1 , f2 )
chebyshev = scipy . spatial . distance . chebyshev ( f1 , f2 )
cityblock = scipy . spatial . distance . cityblock ( f1 , f2 )
correlation = scipy . spatial . distance . correlation ( f1 , f2 )
cosine = scipy . spatial . distance . cosine ( f1 , f2 )
euclidean = scipy . spatial . distance . euclidean ( f1 , f2 )
jensenshannon = scipy . spatial . distance . jensenshannon ( f1 , f2 )
minkowski = scipy . spatial . distance . minkowski ( f1 , f2 )
sqeuclidean = scipy . spatial . distance . sqeuclidean ( f1 , f2 )
wminkowski = scipy . spatial . distance . wminkowski ( f1 , f2 , 1 , np . ones ( len ( f1 )))
output_data = [ braycurtis ,
canberra ,
chebyshev ,
cityblock ,
correlation ,
cosine ,
euclidean ,
jensenshannon ,
minkowski ,
sqeuclidean ,
wminkowski ]
output_data = [ 0 if x != x else x for x in output_data ]
return output_data Dans cette tâche, il y a des analyses d'empreintes digitales qui ont des signaux RRSI de WiFi émettent un environnement dans le centre commercial. First Challange veut que nous estimions la distance entre deux analyses d'empreintes digitales, ce qui est une tâche de régression. Nous avons utilisé Ann (réseaux de neurones artificiels) qui s'inspirent du réseau neuronal biologique. Ann se compose de trois couches; Couche d'entrée, couches cachées (plus d'un) et couche de sortie. Ann commence par la couche d'entrée qui comprend les données d'entraînement (avec des fonctionnalités), transmet les données à la première couche cachée où les données sont calculées par les poids de la première couche cachée. Dans les couches cachées, il y a une itération du calcul des poids aux entrées, puis appliquez-les une fonction d'activation [2]. Comme notre problème est la régression, notre dernière couche est un neurone de sortie unique: sa sortie est la prédite les distances entre les paires de talons d'empreintes digitales. Notre première couche cachée a 64 et le second compte 128 neurones. L'architecture de ce modèle est partagée comme suit. 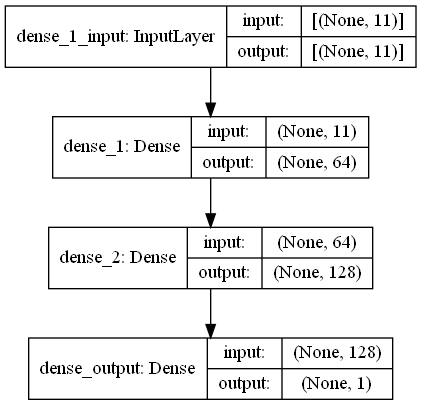
Nous effectuons l'apprentissage en profondeur en utilisant deux fonctions. La fonction create_model façonne les données de formation pour former le modèle et détermine la structure du modèle. La fonction model_features produit un modèle avec la structure spécifiée. Le modèle créé est enregistré pour être utilisé après avoir été formé par la fonction create_model .
## 1.5 Model
import scipy . spatial
import pandas as pd
import numpy as np
import matplotlib . pyplot as plt
from tensorflow import keras
from tensorflow . keras . models import Sequential
from tensorflow . keras . layers import Dense
#from keras.utils.vis_utils import plot_model
% matplotlib inline
def model_features ( i , ii ):
model = Sequential ()
model . add ( Dense ( i , input_shape = ( 11 , ), activation = 'relu' , name = 'dense_1' ))
model . add ( Dense ( ii , activation = 'relu' , name = 'dense_2' ))
model . add ( Dense ( 1 , activation = 'linear' , name = 'dense_output' ))
model . compile ( optimizer = 'adam' , loss = 'mse' , metrics = [ 'mae' ])
model . summary ()
#plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
#print(model.get_config())
return model
def create_model ( name ):
df = pd . read_csv ( name )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X )
y_train = np . array ( df [ df . columns [ - 1 ]])
model = model_features ( 64 , 128 )
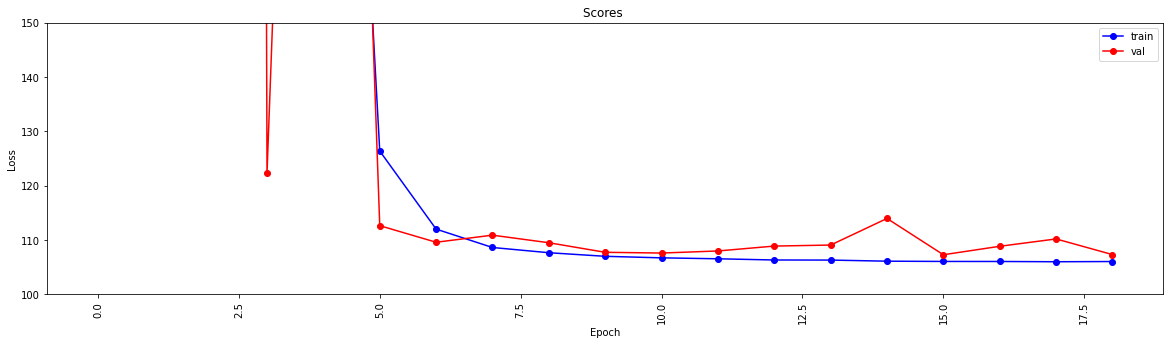
history = model . fit ( X_train , y_train , epochs = 19 , validation_split = 0.5 ) #,batch_size=1)
loss = history . history [ 'loss' ]
val_loss = history . history [ 'val_loss' ]
my_xticks = list ( range ( len ( loss )))
plt . figure ( figsize = ( 20 , 5 ))
plt . plot ( my_xticks , loss , linestyle = '-' , marker = 'o' , color = 'b' , label = "train" )
plt . plot ( my_xticks , val_loss , linestyle = '-' , marker = 'o' , color = 'r' , label = "val" )
plt . title ( "Scores " )
plt . legend ( numpoints = 1 )
plt . ylabel ( "Loss" )
plt . xlabel ( "Epoch" )
plt . xticks ( rotation = 90 )
plt . ylim ([ 100 , 150 ])
plt . show ()
madelname = "./THEMODEL"
model . save ( madelname )
print ( "Model Created!" )
Cette fonction vérifie si les données de formation et de test ont été passées par l'extraction des fonctionnalités. S'ils ne l'ont pas fait, cela crée ces fichiers et le modèle en appelant les fonctions correspondantes. Après avoir manipulé le modèle et toute extraction de caractéristiques, il formate les données de test pour produire les résultats finaux.
## 1.6 Checking the inputs
from numpy import inf
from numpy import nan
def create_new_files ( train , test ):
model_path = "./THEMODEL/"
my_train_file = 'new_train_features.csv'
my_test_file = 'new_test_features.csv'
if os . path . isfile ( my_train_file ) :
pass
else :
print ( "Please wait! Training data feature extraction is in progress... n it will take about 10 minutes" )
feature_extraction_file ( train , my_train_file , 1 )
print ( "TThe training feature extraction completed!!!" )
if os . path . isfile ( my_test_file ) :
pass
else :
print ( "Please wait! Testing data feature extraction is in progress... n it will take about 100-120 minutes" )
feature_extraction_file ( test , my_test_file , 0 )
print ( "The testing feature extraction completed!!!" )
if os . path . isdir ( model_path ):
pass
else :
print ( "Please wait! Creating the deep learning model... n it will take about 10 minutes" )
create_model ( my_train_file )
print ( "The model file created!!! n n n " )
model = keras . models . load_model ( model_path )
df = pd . read_csv ( my_test_file )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X_train = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X_train )
y_train = np . array ( df [ df . columns [ - 1 ]])
predicted = model . predict ( X_train )
print ( "Please wait! Creating resuşts... " )
return predicted Cette étape déclenche des processus d'extraction et de création de modèles et permet à tous les processus de commencer. Ainsi, en utilisant les ID du fichier test1_test.csv , il remplit la troisième colonne (déplacement) avec la distance estimée pour ces paires d'empreintes digitales et il enregistre ce fichier dans le répertoire avec le nom TASK1-MySubmission.csv .
## 1.7 Submission
distance_estimate = create_new_files ( train_data , test_ids )
count = 0
output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
output_data . append ([ id1 , id2 , distance_estimate [ count ][ 0 ]])
count += 1
print ( "Process finished. Preparing result file ..." )
with open ( "TASK1-MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )
print ( "The results are ready. n See MySubmission.csv" ) Please wait! Creating the deep learning model...
it will take about 10 minutes
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 64) 768
_________________________________________________________________
dense_2 (Dense) (None, 128) 8320
_________________________________________________________________
dense_output (Dense) (None, 1) 129
=================================================================
Total params: 9,217
Trainable params: 9,217
Non-trainable params: 0
_________________________________________________________________
Epoch 1/19
13748/13748 [==============================] - 30s 2ms/step - loss: 2007233.6250 - mae: 161.3013 - val_loss: 218.8822 - val_mae: 11.5630
Epoch 2/19
13748/13748 [==============================] - 27s 2ms/step - loss: 24832.6309 - mae: 53.9385 - val_loss: 123437.0859 - val_mae: 307.2885
Epoch 3/19
13748/13748 [==============================] - 26s 2ms/step - loss: 4028.0859 - mae: 29.9960 - val_loss: 3329.2024 - val_mae: 49.9126
Epoch 4/19
13748/13748 [==============================] - 27s 2ms/step - loss: 904.7919 - mae: 17.6284 - val_loss: 122.3358 - val_mae: 6.8169
Epoch 5/19
13748/13748 [==============================] - 25s 2ms/step - loss: 315.7050 - mae: 11.9098 - val_loss: 404.0973 - val_mae: 15.2033
Epoch 6/19
13748/13748 [==============================] - 26s 2ms/step - loss: 126.3843 - mae: 7.8173 - val_loss: 112.6499 - val_mae: 7.6804
Epoch 7/19
13748/13748 [==============================] - 27s 2ms/step - loss: 112.0149 - mae: 7.4220 - val_loss: 109.5987 - val_mae: 7.1964
Epoch 8/19
13748/13748 [==============================] - 26s 2ms/step - loss: 108.6342 - mae: 7.3271 - val_loss: 110.9016 - val_mae: 7.6862
Epoch 9/19
13748/13748 [==============================] - 26s 2ms/step - loss: 107.6721 - mae: 7.2827 - val_loss: 109.5083 - val_mae: 7.5235
Epoch 10/19
13748/13748 [==============================] - 27s 2ms/step - loss: 107.0110 - mae: 7.2290 - val_loss: 107.7498 - val_mae: 7.1105
Epoch 11/19
13748/13748 [==============================] - 29s 2ms/step - loss: 106.7296 - mae: 7.2158 - val_loss: 107.6115 - val_mae: 7.1178
Epoch 12/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.5561 - mae: 7.2039 - val_loss: 107.9937 - val_mae: 6.9932
Epoch 13/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.3344 - mae: 7.1905 - val_loss: 108.8941 - val_mae: 7.4530
Epoch 14/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.3188 - mae: 7.1927 - val_loss: 109.0832 - val_mae: 7.5309
Epoch 15/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.1150 - mae: 7.1829 - val_loss: 113.9741 - val_mae: 7.9496
Epoch 16/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.0676 - mae: 7.1788 - val_loss: 107.2984 - val_mae: 7.2192
Epoch 17/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0614 - mae: 7.1733 - val_loss: 108.8553 - val_mae: 7.4640
Epoch 18/19
13748/13748 [==============================] - 28s 2ms/step - loss: 106.0113 - mae: 7.1790 - val_loss: 110.2068 - val_mae: 7.6562
Epoch 19/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0519 - mae: 7.1791 - val_loss: 107.3276 - val_mae: 7.0981
INFO:tensorflow:Assets written to: ./THEMODELassets
Model Created!
The model file created!!!
Please wait! Creating resuşts...
100%|████████████████████████████████████████████████████████████████████| 5160445/5160445 [00:08<00:00, 610910.29it/s]
Process finished. Preparing result file ...
The results are ready.
See MySubmission.csv
Étant donné que nous avons maintenant une métrique pour évaluer la distance WiFi, notre prochaine tâche consiste à séparer les trajectoires d'un centre commercial (un autre centre commercial à celui utilisé dans le premier défi!) Dans les étages séparés dans lesquels ils appartiennent. Vous pouvez le faire de différentes manières , mais nous suggérons fortement une approche de regroupement de graphiques.
Considérez chaque empreinte digitale WiFi dans les données comme un nœud dans un graphique et que nous pouvons former un bord avec d'autres empreintes digitales dans le graphique en évaluant la similitude de deux empreintes digitales. Nous pouvons attribuer un poids élevé aux bords où nous avons une forte similitude entre les empreintes digitales et un faible poids (ou aucun bord) entre ceux qui ne sont pas similaires. En théorie, une métrique de similitude parfaitement précise séparerait trivialement les sols car nous pourrions exclure tous les bords supérieurs à environ 4 mètres (à peu près la hauteur de 1 étage d'un bâtiment). En réalité, il est probable que nous ferons de faux bords entre les étages et nous devrons briser ces bords.
Commençons par un exemple simple. Considérez le graphique ci-dessous où les couleurs du nœud montrent la véritable classification du sol de l'empreinte digitale et les bords reflètent que nous pensons que ces nœuds existent au même étage. Pour cet exercice, nous avons pré-marqué chaque bord avec son "score d'interdépendance", une métrique qui compte combien de fois ce bord est parcouru en prenant le chemin le plus court entre deux nœuds du graphique. En règle générale, cela révèlera des bords qui indiquent une connectivité élevée et peuvent être des candidats pour le retrait.
Dans cet exemple, utilisez le score de bord de bord pour détecter les communautés graphiques. Renvoyez une liste de listes où chaque subliste contient les ID de nœud des communautés. Remarque C'est juste pour aider votre compréhension du problème et ne compte pas pour la solution réelle.
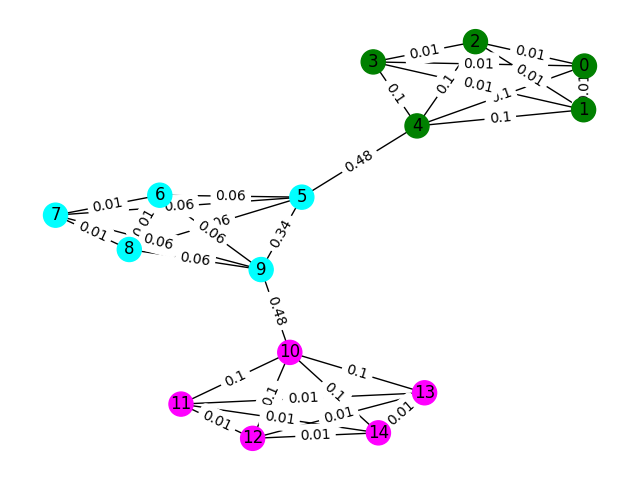
def detect_communities ( Graph ):
## This function should return a list of lists containing
## the node ids of the communities that you have detected.
eb_score = nx . edge_betweenness_centrality ( G )
raise NotImplementedError import networkx as nx
from metrics import check_result
G = nx . read_adjlist ( "graph.adjlist" )
communities = detect_communities ( G )
if check_result ( communities ):
print ( "Correct!" )
else :
print ( "Try again" ) Les exemples de données de formation pour ce problème sont un ensemble de 106981 empreintes digitales ( task2_train_fingerprints.json ) et certains bords entre eux. Nous avons fourni des fichiers qui indiquent trois types de bord différents, qui doivent tous être traités différemment.
task2_train_steps.csv indique des arêtes qui connectent les étapes suivantes dans une trajectoire. Ces bords devraient être très fiables car ils indiquent une certitude que deux empreintes digitales ont été enregistrées à partir du même étage.
task2_train_elevations.csv Indiquez l'opposé des étapes. Ces élévations indiquent que les empreintes digitales sont presque certainement à partir d'un étage différent. Vous pouvez ainsi extrapoler cela si l'empreinte digitale
task2_train_estimated_wifi_distances.csv sont les distances pré-calculées que nous avons calculées en utilisant notre propre métrique de distance. Cette métrique est imparfaite et en tant que telle, nous savons que bon nombre de ces bords seront incorrects (c'est-à-dire qu'ils connecteront deux étages ensemble). Nous suggérons qu'au départ, vous utilisez les bords de ce fichier pour construire votre graphique initial et calculer une solution. Cependant, si vous obtenez un score élevé sur Task1, vous pouvez envisager de calculer vos propres distances WiFi pour créer un graphique.
Votre graphique peut être à l'un des deux niveaux de détail, soit au niveau de la trajectoire ou au niveau des empreintes digitales, vous pouvez choisir la représentation que vous souhaitez utiliser, mais en fin de compte, nous voulons connaître les grappes de trajectoire . Le niveau de trajectoire aurait chaque nœud comme trajectoire et les bords entre les nœuds se produiraient si les empreintes digitales dans leurs trajectoires avaient une similiir élevée. Le niveau d'empreinte digitale aurait chaque empreinte digitale comme nœud. Vous pouvez rechercher l'ID de trajectoire de l'empreinte digitale en utilisant la task2_train_lookup.json pour convertir entre les représentations.
Pour vous aider à déboguer et à former votre solution, nous avons fourni une vérité sur le terrain pour certaines des trajectoires de task2_train_GT.json . Dans ce fichier, les clés sont les ID de trajectoire (comme dans task2_train_lookup.json ) et les valeurs sont le véritable ID de plancher du bâtiment.
L'ensemble de tests est exactement le même format que l'ensemble de formation (pour un bâtiment séparé, nous n'allions pas le rendre aussi facile;)) mais nous n'avons pas inclus le fichier de vérité au sol équivalent. Cela sera retenu pour nous permettre de marquer votre solution.
Points à considérer
Dans cette section, nous fournirons un exemple de code pour ouvrir les fichiers et construire les deux types de graphiques.
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/train"
with open ( os . path . join ( path_to_data , "task2_train_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_train_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_train_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_train_lookup.json" )
gt_path = os . path . join ( path_to_data , "task2_train_GT.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f )
with open ( gt_path ) as f :
gt = json . load ( f )
C'est une façon de construire le graphique au niveau des empreintes digitales, où chaque nœud du graphique est une empreinte digitale. Nous avons ajouté des poids de bord qui correspondent aux distances estimées / vraies des bords WiFi et PDR respectivement. Nous avons également ajouté des bords d'altitude pour indiquer cette relation. Vous voudrez peut-être appliquer explicitement qu'il n'y a aucun de ces bords (ou tout bord d'élévation valide entre les trajectoires) lors du développement de votre solution.
G = nx . Graph ()
for id1 , id2 , dist in tqdm ( steps ):
G . add_edge ( id1 , id2 , ty = "s" , weight = dist )
for id1 , id2 , dist in tqdm ( wifi ):
G . add_edge ( id1 , id2 , ty = "w" , weight = dist )
for id1 , id2 in tqdm ( elevs ):
G . add_edge ( id1 , id2 , ty = "e" )Le graphique de trajectoire n'est sans doute pas aussi simple que vous avez besoin de penser à un moyen de représenter de nombreuses connexions WiFi entre les trajectoires. Dans l'exemple de graphique ci-dessous, nous prenons simplement la distance moyenne en poids, mais est-ce vraiment la meilleure représentation?
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])Votre soumission doit être un fichier CSV où les trajectoires que vous croyez au même étage ont leur index sur la même ligne séparée par des virgules. Chaque nouveau cluster sera entré sur une nouvelle ligne.
Par exemple, consultez l'entrée aléatoire ci-dessous.
import random
random_data = []
n_clusters = random . randint ( 50 , 100 )
for i in range ( 0 , n_clusters ):
random_data . append ([])
for traj in set ( fp_lookup . values ()):
cluster = random . randint ( 0 , n_clusters - 1 )
random_data [ cluster ]. append ( traj )
with open ( "MyRandomSubmission.csv" , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( random_data )Les étapes de la tâche 2 peuvent être résumées comme suit:
Node2vec .TASK2-Mysubmission.csv ) est préparé en fonction de la trajectoire des ID.Ces étapes sont illustrées dans l'image ci-dessous.

Nous avons utilisé Python 3.6.5 pour créer le fichier d'application. Nous avons inclus des modules supplémentaires qui n'ont pas été inclus dans l'exemple de fichier donné au début de la compétition. Ces modules peuvent être répertoriés comme:
| Molules | Tâche |
|---|---|
| scikit-apprend | Apprentissage automatique et préparation des données |
| node2vec | Apprentissage des fonctionnalités évolutives pour les réseaux |
| nombant | Opérations mathématiques |
Nous avons commencé avec l'installation de ces modules comme première étape.
## 2.1 Installing modules
!p ip install node2vec
!p ip install scikit - learn
!p ip install numpy Dans cette étape, nous avons corrigé la graine aléatoire associée à utiliser afin d'obtenir des résultats reproductibles. De cette façon, nous avons fourni un chemin déterministe où nous obtenons le même résultat à chaque cycle. Cependant, selon nos observations, les résultats obtenus sur différents ordinateurs peuvent différer légèrement (± 1%)
## 2.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )Dans cette section, les fichiers donnés pour les données de test sont chargés.
wifi prend des ID et des poids de la task2_test_estimated_wifi_distances.csv .steps de la variable prennent des ID et des poids de la tâche de task2_test_steps.csv .elevs prend des ID de la tâche de task2_test_elevations.csv .fp_lookup obtient des ID et des trajectoires du fichier task2_test_lookup.json . Nous ne préférons pas la méthode de recalcul des distances estimées données dans le WiFi avec le modèle que nous avons obtenu dans Task1, car les résultats que nous avons obtenus à partir de ce processus n'ont pas fait de différence significative. C'est pourquoi nous n'avons pas utilisé le fichier task2_test_fingerprints.json dans notre travail ultime.
## 2.3 Loading the data
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/test"
with open ( os . path . join ( path_to_data , "task2_test_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_test_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_test_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_test_lookup.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f ) 3773297it [00:19, 191689.25it/s]
2767it [00:00, 52461.27it/s]
139537it [00:00, 180082.01it/s]
Nous prenons la distance moyenne comme le poids lors de la création du graphique de trajectoire. Nous avons utilisé l'exemple donné pour la tâche 2 ( Task2-IPS-Challenge-2021.ipynb ) pour ce processus. Nous avons enregistré le graphique résultant ( B ) en tant que liste d'adjacence dans le répertoire (comme my.adjlist ).
## 2.3 Generating the Trajectory graph.
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])
nx . write_adjlist ( B , "my.adjlist" ) 100%|████████████████████████████████████████████████████████████████████| 3773297/3773297 [00:27<00:00, 135453.95it/s]
100%|██████████████████████████████████████████████████████████████████████████████████████| 2767/2767 [00:00<?, ?it/s]
Avant de donner la liste d'adjacence en entrée aux algorithmes d'apprentissage automatique, nous convertissons les nœuds en vecteur. Dans notre travail, nous avons utilisé Node2VEC comme graphique de méthodologie d'algorithme d'intégration proposé par Grover & Leskovec en 2016 [3]. Node2Vec est un algorithme semi-supervisé pour l'apprentissage des caractéristiques des nœuds du réseau. Node2VEC est créé sur la base de la technique de saut-gramme, qui est une approche PNL motivée sur le concept de structure de distribution. La technique de saut-gramme utilise le mot central (entrée) pour prédire les voisins (sortie) tout en calculant les probabilités d'environnement en fonction d'une taille de fenêtre donnée (séquence contigu des éléments avant le centre), en d'autres termes n-grammes. Contrairement à l'approche NLP, le système Node2Vec n'est pas alimenté avec des mots qui ont une structure linéaire, mais des nœuds et des bords, qui ont une structure graphique distribuée. Cette structure multidimensionnelle rend les intégres complexes et coûteux en calcul, mais Node2VEC utilise un échantillonnage négatif avec l'optimisation de la descente de gradient stochastique (SGD) pour y faire face. En plus de cela, l'approche de marche aléatoire est utilisée pour détecter les échantillons de nœuds voisins du nœud source dans une structure non linéaire.
Dans notre étude, nous avons d'abord effectué la représentation vectorielle des relations de nœud dans l'espace de faible dimension en modélisant avec Node2VEC à partir de distance donnée de deux nœuds (poids). Ensuite, nous avons utilisé la sortie de Node2Vec (Graph Embeddings), qui a des vecteurs de nœuds, pour alimenter l'algorithme de clustering K-Means traditionnel.
Les paramètres que nous utilisons dans NOD2VEC peuvent être répertoriés comme suit:
| Hyperparamètre | Valeur |
|---|---|
| dimensions | 32 |
| walk_length | 15 |
| num_walks | 100 |
| ouvriers | 1 |
| graine | 0 |
| fenêtre | 10 |
| min_count | 1 |
| lots | 4 |
Le modèle Node2VEC prend la liste d'adjacence en entrée et publie un vecteur de 32 taille. Dans cette partie, le fichier Node.py est créé et exécuté dans le Jupyter Notebook . Il y a deux raisons pour lesquelles il est préférable d'exécuter à l'extérieur plutôt que dans une cellule de carnet de jupyter.
Node2vec est une méthode très coûteuse, l'erreur de débordement RAM est tout à fait possible si l'exécution dans Jupyter Notebook. La création et l'exécution du modèle Node2vec à l'extérieur évite cette erreur. La cellule ci-dessous crée le fichier nommé Node.py. Ce fichier crée le modèle Node2Vec. Ce modèle prend la liste d'adjacence ( my.adjlist ) en entrée et crée un fichier vectoriel à 32 dimensions sous forme de sortie ( vectors.emb ).
Important! Le code ci-dessous doit être exécuté dans les distributions Linux (testées dans Google Colab et Ubuntu).
# 2.4 Converting nodes to vectors
# A folder named tmp is created. This folder is essential for the node2vec model to use less RAM.
try :
if not os . path . exists ( "tmp" ):
os . makedirs ( "tmp" )
except OSError :
print ( "The folder could not be created! n Please manually create the " tmp " folder in the directory" )
node = """
# importing related modules
from node2vec import Node2Vec
import networkx as nx
#importing adjacency list file as B
B = nx.read_adjlist("my.adjlist")
seed_value=0
# Specifying the input and hyperparameters of the node2vec model
node2vec = Node2Vec(B, dimensions=32, walk_length=15, num_walks=100, workers=1,seed=seed_value,temp_folder = './tmp')
#Assigning/specifying random seeds
import os
os.environ['PYTHONHASHSEED']=str(seed_value)
import random
random.seed(seed_value)
import numpy as np
np.random.seed(seed_value)
# creation of the model
model = node2vec.fit(window=10, min_count=1, batch_words=4,seed=seed_value)
# saving the output vector
model.wv.save_word2vec_format("vectors.emb")
# save the model
model.save("vectorMODEL")
"""
f = open ( "node.py" , "w" )
f . write ( node )
f . close ()
! PYTHONHASHSEED = 0 python3 node . py Une fois notre fichier vectoriel créé, nous lisons ce fichier ( vectors.emb ). Ce fichier se compose de 33 colonnes. La première colonne est le numéro de nœud (IDS) et reste sont des valeurs vectorielles. En triant l'intégralité du fichier par la première colonne, nous renvoyons les nœuds à leur commande d'origine. Ensuite, nous supprimons cette colonne ID, que nous n'utiliserons plus. Ainsi, nous donnons la forme finale de nos données. Nos données sont prêtes à être utilisées dans les applications d'apprentissage automatique.
# 2.4 Reshaping data
vec = np . loadtxt ( "vectors.emb" , skiprows = 1 )
print ( "shape of vector file: " , vec . shape )
print ( vec )
vec = vec [ vec [:, 0 ]. argsort ()];
vec = vec [ 0 : vec . shape [ 0 ], 1 : vec . shape [ 1 ]] shape of vector file: (11162, 33)
[[ 9.1200000e+03 3.9031842e-01 -4.7147268e-01 ... -5.7490986e-02
1.3059708e-01 -5.4280665e-02]
[ 6.5320000e+03 -3.5591956e-02 -9.8558587e-01 ... -2.7217887e-02
5.6435770e-01 -5.7787680e-01]
[ 5.6580000e+03 3.5879680e-01 -4.7564098e-01 ... -9.7607370e-02
1.5506668e-01 1.1333219e-01]
...
[ 2.7950000e+03 1.1724627e-02 1.0272172e-02 ... -4.5596390e-04
-1.1507459e-02 -7.6738600e-04]
[ 4.3380000e+03 1.2865483e-02 1.2103912e-02 ... 1.6619096e-03
1.3672550e-02 1.4605848e-02]
[ 1.1770000e+03 -1.3707868e-03 1.5238028e-02 ... -5.9994194e-04
-1.2986251e-02 1.3706315e-03]]
La tâche-2 est un problème de clustering. La prémisse que nous devons décider lors de la résolution de ce problème est le nombre de clusters dans lesquels nous devons diviser. Pour cela, nous avons essayé différents numéros de cluster et comparé les scores que nous avons obtenus. Le graphique ci-dessous montre la comparaison du nombre de clusters et le score obtenu. Comme on peut le voir à partir de ce graphique, le nombre de grappes a augmenté en continu entre 5 et 21, avec quelques fluctuations d'exception, et stabilisé après 21. Pour cette raison, nous nous sommes concentrés sur le nombre de grappes entre 21 et 23 dans notre étude.
# 2.5 Determine the number of clusters
import numpy as np
import matplotlib . pyplot as plt
import seaborn as sns
import matplotlib
% matplotlib inline
sns . set_style ( "whitegrid" )
agglom = [ 24.69 , 28.14 , 28.14 , 28.14 , 30 , 33.33 , 40.88 , 38.70 , 40 , 40 , 40 , 29.12 , 45.85 , 45.85 , 48.00 , 50.17 , 57.83 , 57.83 , 57.83 ]
plt . figure ( figsize = ( 10 , 5 ))
plt . plot ( range ( 5 , 24 ), agglom )
matplotlib . pyplot . xticks ( range ( 5 , 24 ))
plt . title ( 'Number of clusters and performance relationship' )
plt . xlabel ( 'Number of clusters' )
plt . ylabel ( 'Score' )
plt . show ()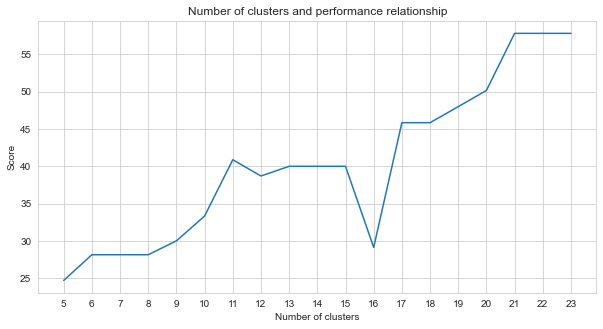
Parmi les méthodes d'apprentissage automatique non supervisées que nous avons essayées (comme les k-means, le clustering agglomératif, la propagation d'affinité, le changement moyen, le clustering spectral, le DBSCAN, l'optique, le bouleau, le mini-lots K-means), nous avons obtenu les meilleurs résultats en utilisant K-Means avec 23 clusters.
K-Means est un algorithme de clustering est l'une des techniques d'apprentissage automatique non supervisées de base et traditionnelles qui font des hypothèses pour trouver des groupes homogènes ou naturels d'éléments (grappes) en utilisant des données non étiquetées. Les clusters sont des points de points (nœuds de nos données) regroupés qui partagent des similitudes particulières. K-Means a besoin du nombre cible de centroïdes qui fait référence au nombre de groupes dans les données que les données doivent être divisées. L'algorithme commence par le groupe de centroïdes assignés au hasard, puis continuez les itérations pour en trouver les meilleures positions. L'algorithme attribue les points / nœuds aux centroïdes désignés en utilisant en cluster la somme des carrés du membre des points, il s'agit de continuer à mettre à jour et à déménager [4]. Dans notre exemple, le nombre de centroïdes reflète le nombre d'étages. Il convient de noter que cela ne fournit pas d'informations sur l'ordre des étages.
Ci-dessous, la demande K-Means a été faite pour 23 clusters.
# 2.5 Best result
from sklearn import cluster
import time
ML_results = []
k_clusters = 23
algorithms = {}
algorithms [ 'KMeans' ] = cluster . KMeans ( n_clusters = k_clusters , random_state = 10 )
second = time . time ()
for model in algorithms . values ():
model . fit ( vec )
ML_results = list ( model . labels_ )
print ( model , time . time () - second ) KMeans(n_clusters=23, random_state=10) 1.082334280014038
La sortie de l'algorithme d'apprentissage automatique détermine à laquelle appartient les empreintes digitales. Mais ce qui est exigé de nous, c'est de regrouper les trajectoires. Par conséquent, ces empreintes digitales sont converties en leurs homologues de trajectoire à l'aide de la variable fp_lookup . Cette sortie est traitée dans le fichier TASK2-Mysubmission.csv .
## 2.6 Submission
result = {}
for ii , i in enumerate ( set ( fp_lookup . values ())):
result [ i ] = ML_results [ ii ]
ters = {}
for i in result :
if result [ i ] not in ters :
ters [ result [ i ]] = []
ters [ result [ i ]]. append ( i )
else :
ters [ result [ i ]]. append ( i )
final_results = []
for i in ters :
final_results . append ( ters [ i ])
name = "TASK2-Mysubmission.csv"
with open ( name , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( final_results )
print ( name , "file is ready!" ) TASK2-Mysubmission.csv file is ready!
[1] P. Contributeurs de Scipy et Scipy 1.0. SCIPY 1.0: Algorithmes fondamentaux pour l'informatique scientifique dans Python. Nature Methods, 17: 261--272, 2020.
[2] A. Geron, apprentissage automatique pratique avec Scikit-Learn, Keras et Tensorflow: concepts, outils et techniques pour construire des systèmes intelligents. O'Reilly Media, 2019
[3] A. Grover, J. Leskovec. ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), 2016.
[4] Jin X., Han J. (2011) K-Means Clustering. Dans: Sammut C., Webb GI (eds) Encyclopedia of Machine Learning. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-30164-8_425