Noise Reduction
1.0.0
À propos du projet
Pile technologique
Structure de fichiers
Commencer
Résultats et démo
Travail futur
Contributeurs
Remerciements et ressources
Licence
Le bruit devait être retiré qui est naturellement induit comme le bruit non environnemental qui est supprimé avec le déniisation du signal. Reportez-vous à cette documentation également ce blog sur la réduction du bruit d'IA
La bibliothèque Librosa pour la manupulation audio est utilisée.
Pour les signaux audio, nous avons utilisé Scipy
Matplotlib utilisé pour manipuler les données et visualiser le signal.
Le reste est Numpy pour les opérations mathématiques, WAVE pour l'opération sur le fichier WAVE.
Noise Reduction ├───docs ## Documents and Images │ └───Input Audio file ├─── Project Details │ | │ ├─── │ │ ├───Research papers │ │ ├───Linear Algebra │ │ ├───Neural networks & Deep Learning │ │ ├───Project Documentation │ │ ├───AI Noise Reduction Blog │ │ ├───AI Noise Reduction Report │ │ └───Code Implementation │ │ ├───AI Noise Reduction.py │ │ ├───audio.wav │ │ ├───Resources
Testé sous Windows
Git Clone https://github.com/dhriti03/noise-reduction.gitcd Noise-Reduction
Dans votre cahier, installez certaines bibliothèques
Pip Install Wave pip install librosa pip install scipy.io pip install matplotlib.potplot
* Ceci est le fichier audio d'origine *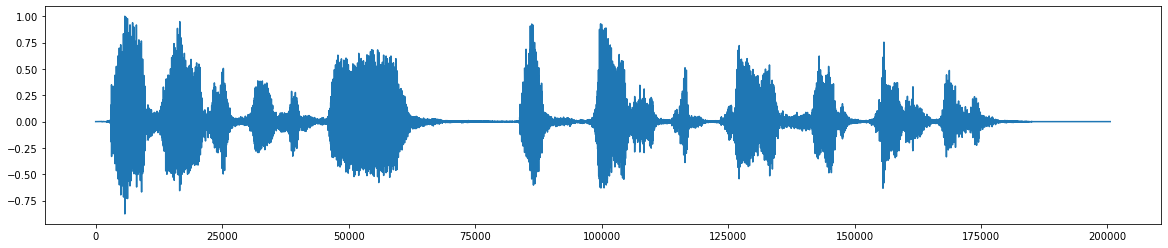 
* Après l'ajout du bruit * 
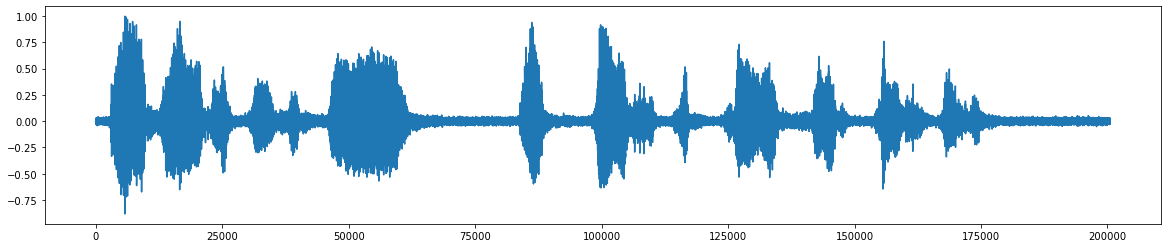* Le signal audio final après avoir retiré le bruit * 
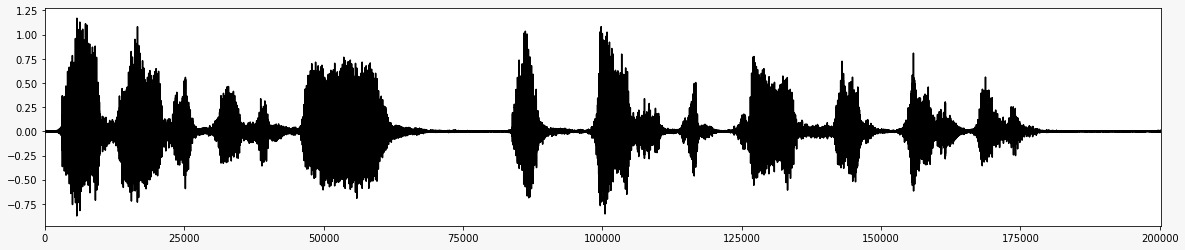* Organigramme pour le projet *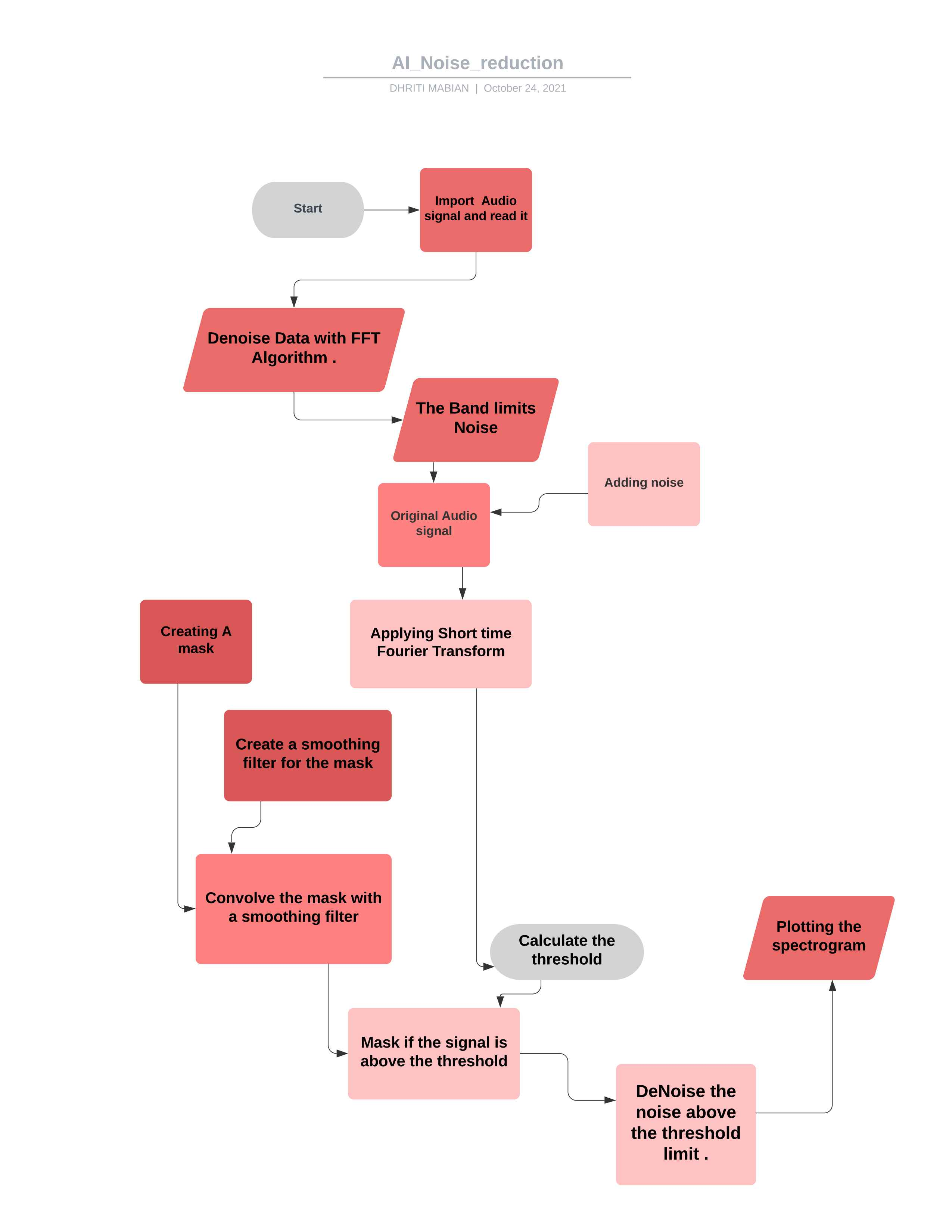 
En manipulant le code en fonction de vos exigences, vous pouvez l'utiliser pour contrôler la plupart des Signlas audio. ##Théorie
Une FFT est calculée sur le clip audio du bruit
Les statistiques sont calculées sur FFT du bruit (en fréquence)
Un seuil est calculé sur la base des statistiques du bruit (et de la sensibilité souhaitée de l'algorithme)
Un masque est déterminé en comparant le signal FFT au seuil
Le masque est lissé avec un filtre sur la fréquence et le temps
Le masque est applaudie à la FFT du signal et est inversé
Importer ipython à partir de scipy.io Importer wavfileimport scipy.signalimport numpy comme npimport matplotlib.pot en tant que pltimport librosaimport wave% matplotlib inline
Ici, nous importons les bibliothèques comme l' Ipython Lib utilisé pour créer un environnement complet pour l'informatique interactive et exploratoire.
De la bibliothèque Scipy.io est utilisée pour manipuler les données et la visualisation des données à l'aide d'une large gamme de commandes Python.
Numpy contient un réseau multidimensionnel et des structures de données matricielles. Il peut être utilisé pour effectuer un certain nombre d'opérations mathématiques sur des tableaux tels que les routines trigonométriques, statistiques et algébriques est donc une bibliothèque très utile.
La bibliothèque Matplotlib.pyplot aide à comprendre l'énorme quantité de données grâce à différentes visualisations.
Librosa utilisé lorsque nous travaillons avec des données audio comme dans la génération de musique (en utilisant LSTM), reconnaissance automatique de la parole. Il fournit les éléments constitutifs nécessaires pour créer les systèmes de récupération des informations musicales.
% Matplotlib en ligne pour activer le traçage en ligne, où les graphiques / graphiques seront affichés juste en dessous de la cellule où vos commandes de traçage sont écrites. Il fournit une interactivité avec le backend dans les fronts comme le cahier Jupyter.
wav_loc = r '/ home / noise_reduction / downloads / wave / file.wav'rate, data = wavfile.read (wav_loc, mmap = false)
Ici, nous prenons l'emplacement du chemin du fichier WAW, puis lions ce fichier WAW avec le module WaveFile qui est de la bibliothèque Scipy.io . avec les paramètres (nom de fichier - chaîne ou poignée de fichier ouvrir qui est un fichier WAV d'entrée.) Ensuite, le (mmap: bool, facultatif dans lequel il faut lire les données comme mappée par la mémoire (par défaut: false).
def fftnoise (f): f = np.array (f, dtype = "complex") np = (len (f) - 1) // 2Phases = np.random.rand (np) * 2 * np.piphases = np .cos (phases) + 1j * np.sin (phases) f [1: np + 1] * = phasesf [-1: -1 - np: -1] = np.conj (f [1: np + 1] ) retourner np.fft.ifft (f) .real
Ici, nous définissons d'abord la fonction de bruit FFT en bref, une transformée de Fourier rapide (FFT) est un algorithme qui calcule la transformée de Fourier discrète (DFT) d'une séquence, ou son inverse (IDFT). L'analyse de Fourier convertit un signal de son domaine d'origine (souvent du temps ou de l'espace) en une représentation dans le domaine fréquentiel et vice versa. Le DFT est obtenu en décomposant une séquence de valeurs en composants de différentes fréquences.
En utilisant une transformation rapide de Fourier et en définissant une fonction du complexe de type de données et en calculant enfin la partie réelle de la fonction. En cela, les fréquences allant entre la fréquence minimale et la fréquence maximale sont définies sur 1 et le repos indésirable sont négligés.
Donner l'emplacement du fichier
Lire le fichier WAV
-32767 à +32767 est un son bon (être symétrique) et 32768 signifie que l'audio coupé à ce moment-là
Le fichier WAV est entier 16 bits, la plage est [-32768, 32767], divisant ainsi par 32768 (2 ^ 15) donnera la plage de complément TwOS appropriée de [-1, 1]
DEF BAND_LIMITE_NOISE (MIN_FREQ, MAX_FREQ, Samples = 1024, Samplerate = 1): Freqs = NP.ABS (NP.FFT.FFTFREQ (Samples, 1 / Samplerate)) F = NP.ZEROS (Samples) F [NP.Logical_and (Freqs > = min_freq, freqs <= max_freq)] = 1return fftnoise (f)
Une fonction ou une série chronologique dont la transformée de Fourier est limitée à une gamme finie de fréquences ou de longueurs d'onde.
Définition du FREQ avec le FREQ standard avec la limite MIN et MAX.
Noise_len = 2 # secondsnoise = band_limited_noise (min_freq = 4000, max_freq = 12000, samples = len (data), samplerate = rate) * 10noise_clip = bruit [: rate * bruit_len] audio_clip_band_limite
Le bloc de bruit blanc limité en bande spécifie un spectre à deux faces, où les unités sont Hz.
où le maximum de 12000 et Min Freq de 4000 sont comparés par le bruit et les données fournies.
Ici, nous couvrons le signal de bruit en ayant un produit de vitesse et le Len du signal de bruit.
ajoutant ainsi le bruit et les données données
En effet, l'ajout de bruit étend la taille de l'ensemble de données de formation.
Un bruit aléatoire est ajouté aux variables d'entrée les rendant différents à chaque fois qu'il est exposé au modèle.
L'ajout de bruit aux échantillons d'entrée est une forme simple d'augmentation des données.
L'ajout de bruit signifie que le réseau est moins en mesure de mémoriser des échantillons de formation car ils changent tout le temps,
entraînant des poids de réseau plus petits et un réseau plus robuste qui a une erreur de généralisation plus faible.
importer du délai datetime importe timeldelta comme TD
Temps d'importation Ce module fournit diverses fonctions liées au temps. Pour les fonctionnalités connexes, voir également les modules DateTime et Calendar. classe DateTime.Timedelta
Une durée exprimant la différence entre deux instances de date, de temps ou de Datetime à la résolution microseconde.
DEF _STFT (Y, n_fft, hop_length, win_length): return Librosa.stft (y = y, n_fft = n_fft, hop_length = hop_length, win_length = win_length)
Une transformation de Fourier à court terme peut être utilisée pour quantifier le changement de la fréquence et le contenu de phase d'un signal non stationnaire au fil du temps.
La longueur du houblon doit se référer au nombre d'échantillons entre les images successives. Pour l'analyse du signal, la longueur du houblon doit être inférieure à la taille de la trame, de sorte que les trames se chevauchent.
Paramètres ynp.ndArray [forme = (n,)], signal d'entrée à valeur réelle
n_fftint> 0 [scalar]
Longueur du signal fenêtré après rembourrage avec des zéros. Le nombre de lignes dans la matrice STFT D est (1 + n_fft / 2) . La valeur par défaut, n_fft = 2048 échantillons, correspond à une durée physique de 93 millisecondes à une fréquence d'échantillonnage de 22050 Hz, c'est-à-dire la fréquence d'échantillonnage par défaut en librosa. Cette valeur est bien adaptée aux signaux musicaux. Cependant, dans le traitement de la parole, la valeur recommandée est de 512, correspondant à 23 millisecondes à une fréquence d'échantillonnage de 22050 Hz. Dans tous les cas, nous vous recommandons de définir N_FFT sur une puissance de deux pour optimiser la vitesse de l'algorithme Fast Fourier Transform (FFT).
hop_lengthint> 0 [scalar]
Nombre d'échantillons audio entre les colonnes STFT adjacentes.
Des valeurs plus petites augmentent le nombre de colonnes en D sans affecter la résolution de fréquence du STFT.
S'il n'est pas spécifié, par défaut à win_length // 4 (voir ci-dessous).
win_lengthint <= n_fft [scalar]
Chaque trame de l'audio est fendue par fenêtre de la longueur win_length, puis rembourrée avec des zéros pour correspondre à N_FFT .
Des valeurs plus petites améliorent la résolution temporelle du STFT (c'est-à-dire la capacité de discriminer les impulsions qui sont étroitement espacées) au détriment de la résolution de fréquence (c'est-à-dire la capacité de discriminer les tons purs qui sont étroitement espacés en fréquence). Cet effet est connu sous le nom de compromis de localisation temporelle et doit être ajusté en fonction des propriétés du signal d'entrée y.
S'il n'est pas spécifié, par défaut à win_length = n_fft .
return librosa.istft (y, hop_length, win_length)
Transformée de Fourier à court terme inverse (ISTFT). Convertit le spectrogramme à valeur complexe STFT_MATRIX vers la série temporelle Y en minimisant l'erreur quadratique moyenne entre STFT_MATRIX et STFT de Y comme décrit dans
En général, la fonction de fenêtre, la longueur du houblon et d'autres paramètres devraient être les mêmes que dans STFT, ce qui conduit principalement à une reconstruction parfaite d'un signal à partir de STFT_MATRIX non modifié.
def _amp_to_db (x): return Librosa.core.amplitude_to_db (x, ref = 1.0, amin = 1e-20, top_db = 80.0)
1. Convertissez un spectrogramme d'amplitude dans le spectrogramme à l'échelle DB.C'est équivalent à Power_TO_DB (S ** 2), mais est fourni pour la commodité.
return librosa.core.db_to_amplitude (x, ref = 1.0)
Convertissez un spectrogramme à l'échelle DB en un spectrogramme d'amplitude.
Cela inverse efficacement Amplitude_to_db:
db_to_amplitude (s_db) ~ = 10.0 (0,5 * (s_db + log10 (ref) / 10)) **
DEF PLOT_SPECTROgram (Signal, Title): Fig, AX = PLT.SUBPLOTS (FigSize = (20, 4)) CAX = AX.MATSHOW (Signal, Origin = "Lower", Aspect = "Auto", CMAP = PLT.CM. sismique, vmin = -1 * np.max (np.abs (signal)), vmax = np.max (np.abs (signal)),
)Tracer le spectogramme avec le signal comme entrée.
La classe des axes contient la plupart des éléments de figure: axe, tique, line2d, texte, polygone, etc., et définit le système de coordonnées.
Il fournit plusieurs cartes de couleurs dans Matplotlib accessibles via cette fonction .O Trouvez une bonne représentation dans l'espace couleurs 3D pour votre ensemble de données.
Fig.Colorbar (Cax) ax.set_title (titre)
La meilleure façon de voir ce qui se passe, est d'ajouter une barre de couleur (plt.colorbar (), après avoir créé le tracé de dispersion). Vous remarquerez que vos valeurs de sortie entre 0 et 10000 sont toutes inférieures à la partie la plus basse de la barre, où les choses sont un vert très clair.
En général, les valeurs inférieures à VMIN seront colorées avec la couleur la plus basse, et les valeurs supérieures à Vmax obtiendront la couleur la plus élevée.
Si vous définissez Vmax plus petit que VMIN, en interne, ils seront échangés. Bien que, selon la version exacte de Matplotlib et les fonctions précises appelées, Matplotlib pourrait donner un avertissement d'erreur. Donc, mieux vaut définir VMIN toujours inférieur à Vmax.
Def Plot_statistics_and_filter (Mean_freq_noise, std_freq_noise, Noise_Thresh, Smoothing_Filter): Fig, ax = plt.Subplots (ncols = 2, figsize = (20, 4)) plt_std, = ax [0] .plot (std_freq_NoUse, étiquette = "std. Power. de bruit ")
PLT_STD, = AX [0] .plot (Noise_Thresh, label = "Seuil de bruit (par fréquence)") AX [0] .set_title ("Seuil pour masque")
ax [0] .leGend () Cax = ax [1] .matshow (lishing_filter, origin = "inférieur") Fig.Colorbar (Cax) ax [1] .set_title ("filtre pour le masque de lissage")Complote les statistiques de base de la réduction du bruit.
Le rapport signal / bruit (SNR ou S / N) est une mesure utilisée dans la science et l'ingénierie qui compare le niveau d'un signal souhaité au niveau de bruit de fond.
Le SNR est défini comme le rapport de la puissance du signal à la puissance de bruit, souvent exprimé en décibels.
Un rapport supérieur à 1: 1 (supérieur à 0 dB) indique plus de signal que de bruit.
Configuration de la fréquence de seuil pour le masquage du bruit.
Le seuil de masquage fait référence à un processus où un son est rendu inaudible en raison de la présence d'un autre son.
Le seuil de masquage est donc le niveau de pression du son d'un son nécessaire pour rendre le son audible en présence d'un autre bruit appelé "masqueur"
Ainsi ajouté le seuil.
Signaux de bruit flou avec divers filtres à passes basses
Appliquer des filtres sur mesure aux images (convolution 2D)
def removenoise (# pour en moyenne le signal (tension) de la partie de pente positive (montée) d'une onde de triangle pour essayer d'éliminer autant de bruit que possible. Audio_clip, # Ces clips sont les paramètres utilisés sur lesquels nous ferions le respect Operations Noise_clip, n_grad_freq = 2, # Combien de canaux de fréquence à lisser avec le masque.n_grad_time = 4, # Combien de canaux de temps à lisser avec le mask.n_fft = 2048, # Numéro Audio des cadres entre les colonnes STFT.win_length = 2048, # Chaque trame d'audio est fendue par `Window ()`. n_std_thresh = 1,5, # combien d'écarts-types plus forts que la dB moyenne du bruit (à chaque niveau de fréquence) pour être considéré , # Flag vous permet d'écrire des expressions régulières qui semblent présentables Visuelle = FALSE, #WHETHETH pour tracer les étapes de l'algorithme):
def removenoise ( pour en moyenne le signal (tension) de la partie de pente positive (montée) d'une onde de triangle pour essayer d'éliminer autant de bruit que possible.
Audio_clip,
Ces clips sont les paramètres utilisés sur lesquels nous ferions les opérations respectives
Noise_clip, n_grad_freq = 2 combien de canaux de fréquence à lisser avec le masque.
n_grad_time = 4, combien de canaux de temps à lisser avec le masque.
n_fft = 2048
Numéro Audio de trames entre les colonnes STFT.
win_length = 2048, chaque trame d'audio est fendue par window() . La fenêtre sera de la longueur win_length puis rembourrée avec des zéros pour correspondre n_fft ..
hop_length = 512, audio numéro de trames entre les colonnes STFT.
n_std_thersh = 1,5 combien d'écarts-types plus forts que la base de données moyenne du bruit (à chaque niveau de fréquence) à considérer le signal
prop_decrease = 1,0, dans quelle mesure devez-vous diminuer le bruit (1 = tout, 0 = aucun)
Verbose = false,
Le drapeau vous permet d'écrire des expressions régulières qui semblent présentables Visual = FALSE, #WHETHETH pour tracer les étapes de l'algorithme):
noise_stft = _stft (bruit_clip, n_fft, hop_length, win_length) noise_stft_db = _amp_to_db (np.abs (bruit_stft))
STFT sur le bruit
convertir en db
Mean_freq_noise = np.mean (noise_stft_db, axe = 1) std_freq_noise = np.std (bruit_stft_db, axe = 1) noise_thresh = mean_freq_noise + std_freq_noise * n_stdreshs
Calculer les statistiques sur le bruit
Ici, nous pour le bruit de seuil, nous ajoutons la moyenne et le bruit standard et le bruit N_STD.
sig_stft = _stft (Audio_clip, n_fft, hop_length, win_length) sig_stft_db = _amp_to_db (np.abs (sig_stft))
STFT sur Signal
mask_gain_db = np.min (_amp_to_db (np.abs (sig_stft)))
Calculer la valeur pour masquer la base de données pour
smoothing_filter = np.outer (np.concatenate (
[np.linspace (0, 1, n_grad_freq + 1, endpoint = false), np.linspace (1, 0, n_grad_freq + 2),
]]
) [1: -1], np.concatenate (
[np.linspace (0, 1, n_grad_time + 1, endpoint = false), np.linspace (1, 0, n_grad_time + 2),
]]
) [1: -1],
) Smoothing_Filter = Smoothing_Filter / NP.Sum (Smoothing_Filter)Créez un filtre de lissage pour le masque en temps et en fréquence
db_thresh = np.repeat (np.rehape (noise_thresh, [1, len (mean_freq_noise)]), np.shape (sig_stft_db) [1], axe = 0,
) .TCalculez le seuil pour chaque bac de fréquence / temps
SIG_MASK = SIG_STFT_DB <DB_THRESH
masque pour le signal
sig_mask = scipy.signal.fftconvolve (sig_mask, listing_filter, mode = "même") sig_mask = sig_mask * prop_decrease
Convolution de masque avec filtre de lissage
# masque le signalsig_stft_db_masked = (sig_stft_db * (1 - sig_mask) + np.ones (np.shape (mask_gain_db)) * mask_gain_db * sig_mask) _to_amp (sig_stft_db_masked) * np.sign (sig_stft)) + (1j * sig_imag_masked)
Masquer le signal
# Récupérez le signalRecovered_signal = _istft (sig_stft_amp, hop_length, win_length) récupéré_spec = _amp_to_db (np.abs (_stft (récupéré_signal, n_fft, hop_length, win_length)))
)récupérer le signal
Appliquez ainsi un masque si le signal est au-dessus du seuil
Confirmez le masque avec un filtre de lissage
Appliquer l'algorithum de réduction du bruit pour le fichier WAV déjà téléchargé.
Appliquer la FFT sur l'enregistrement en direct du signal audio.
Plus de mise en œuvre plus profonde de l'IA pour l'annulation du bruit.
Application de l'algorithum de réduction du bruit pour divers formats de fichiers audio.
Le signal audio en direct avec le microphone et ESP32 et obtiendra donc le fichier WAV pour le calcul et le traitement du signal supplémentaires.
Dhriti Mabian
Priyal Awankar
* Sra vjti_eklavya 2021
Shreyas atre
Shah Shah
Audace
Méthode d'annulation du bruit
A pris la buissier de plaque de Martin Heinz
Tim Sainburg
Licence
