Des tests d'équivalence peuvent être appliqués pour évaluer si un effet observé d'un prédicteur individuel dans un modèle de régression multiple est suffisamment petit pour être considéré comme statistiquement et pratiquement négligeable (Alter & Counsell, 2021). Pour plus d'informations, veuillez vous référer à la page OSF et / ou à une préimprimée librement disponible sur PSYARXIV.
Les fonctions suivantes offrent des alternatives basées sur l'équivalence appropriées pour conclure un effet négligeable entre un prédicteur et le résultat dans la régression multiple
Ces fonctions R sont conçues pour s'adapter à plusieurs contextes de recherche sans effort, avec ou sans accès à l'ensemble de données complet. Les deux fonctions, reg.equiv.fd() et reg.equiv() , fournissent une sortie similaire mais diffèrent sur le type d'informations d'entrée requises par l'utilisateur.
Plus précisément, la première fonction, reg.equiv.fd() , nécessite l'ensemble de données complet et le modèle dans R (objet lm ), contrairement au second. Le reg.equiv() est destiné aux chercheurs qui n'ont pas accès à l'ensemble de données complet mais qui souhaitent toujours évaluer le manque d'association d'un certain prédicteur avec la variable de résultat dans la régression multiple, par exemple, en utilisant des informations généralement présentées dans une section de résultats ou Tableau rapporté dans un article publié.
reg.equiv.fd() : l'ensemble de données complet requisdatfra= une trame de données (par exemple, mtcars)model= le modèle, un objet LM (par exemple, mod1 , où mod1<- mpg~hp+cyl )delta= la plus petite taille d'effet d'intérêt (sésoi), la taille de l'effet minimalement significative (MME) ou la limite supérieure de l'intervalle d'équivalence (?) (Par exemple, .15)predictor= le nom du prédicteur à tester (par exemple, "cyl" )test= Le type de test est défini automatiquement sur deux tests unilatéraux (TOST; Schuirmann, 1987), l'autre option est l'Anderson-Hauck (AH; Anderson et Hauck, 1983)std= le delta (ou, sesoi) est l'ensemble comme standardisé par défaut. Indiquer std=FALSE pour supposer des unités non standardiséesalpha= Le taux d'erreur nominal de type I est défini sur 0,05 par défaut. Pour changer, indiquez simplement le niveau alpha. Par exemple, alpha=.10 reg.equiv.fd() Exemple: 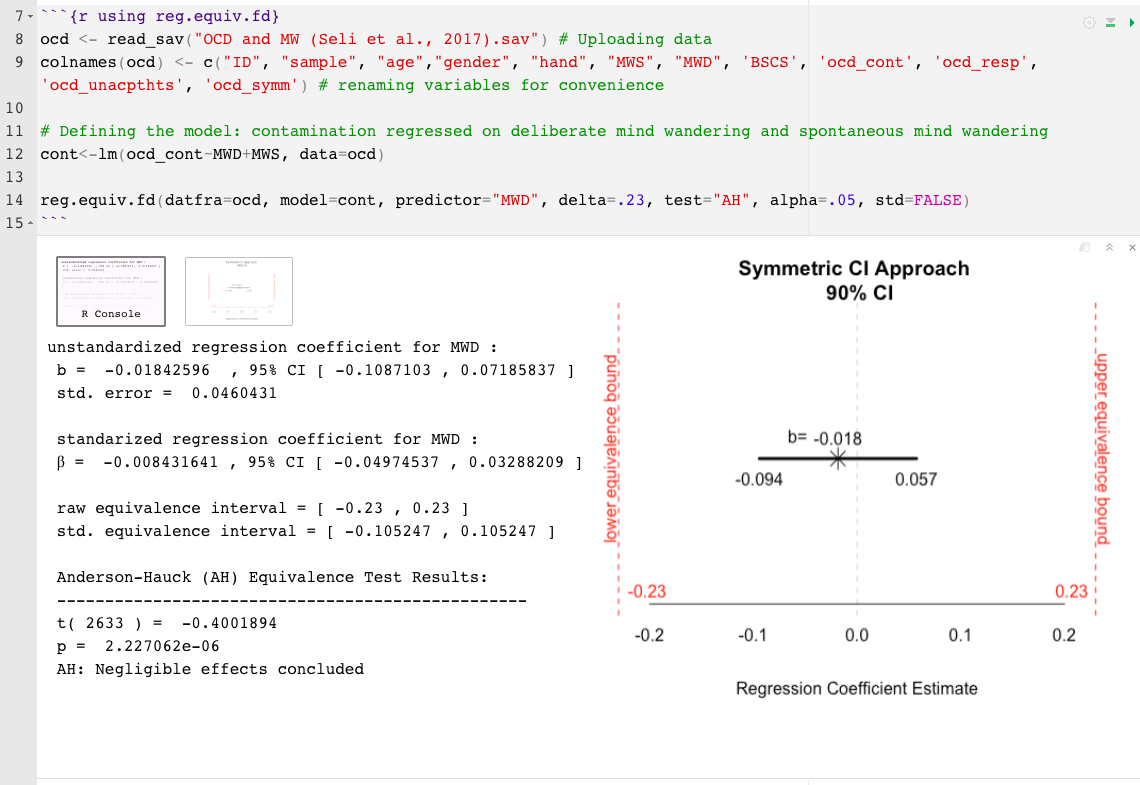
reg.equiv() : ensemble de données complet non requisb= la taille de l'effet estimée associée au prédicteur d'intérêt, cela pourrait être standardisé ou non standardisé (par exemple, 0,02)se= l'erreur standard associée à la taille de l'effet du prédicteur d'intérêt (si la taille de l'effet est standardisée, assurez-vous que la valeur se est liée à l'effet standardisé et non à l'effet brut)p= le nombre de prédicteurs totaux dans le modèle de régression (à l'exclusion de l'interception)n= taille de l'échantillondelta= la plus petite taille d'effet d'intérêt (sésoi), la taille de l'effet minimalement significative (MME) ou la limite supérieure de l'intervalle d'équivalence (?) (Par exemple, .15)predictor= le nom du prédicteur à tester (par exemple, "cyl" )test= Le type de test est défini automatiquement sur deux tests unilatéraux (TOST; Schuirmann, 1987), l'autre option est l'Anderson-Hauck (AH; Anderson et Hauck, 1983)std= le delta (ou, sesoi) et la taille de l'effet indiquée sont définis comme standardisé par défaut. Indiquer std=FALSE pour supposer des unités non standardiséesalpha= Le taux d'erreur nominal de type I est défini sur 0,05 par défaut. Pour changer, indiquez simplement le niveau alpha. Par exemple, alpha=.10 reg.equiv() Exemple: 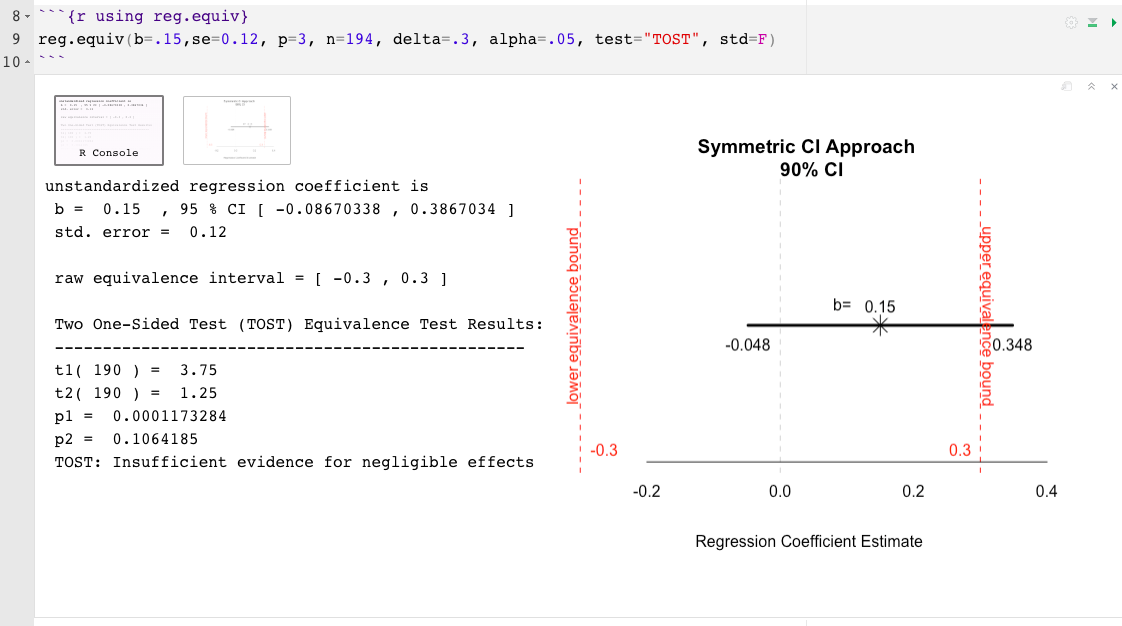
Les tests d'équivalence sont une méthode conçue dans le cadre de tests de signification de l'hypothèse nulle (NHST). NHST a été fortement critiqué pour sa dépassement sur les résultats dichotomiques des valeurs de P avec peu, ou pas de considération de l'ampleur de l'effet ou de ses implications dans la pratique (par exemple, Cumming, 2012; Fidler et Loftus, 2009; Harlow, 1997; Kirk, 2003 ; Lee, 2016 2014). Les chercheurs doivent être conscients des limites de la NHST et démêler les aspects pratiques et statistiques des résultats des tests.
Pour minimiser les limites des valeurs de P , il est plus informatif d' interpréter l'ampleur et la précision de l'effet observé au-delà de la conclusion des «effets négligeables» ou des «preuves insuffisantes des effets négligeables». Les effets observés doivent être interprétés en relation avec les limites d'équivalence, l'étendue de leur incertitude et leurs implications pratiques (ou leur absence) . Pour cette raison, les deux fonctions R offertes ici incluent également une représentation graphique de l'effet observé et de son incertitude associée par rapport à l'intervalle d'équivalence. Le tracé résultant aide à illustrer à quel point l'effet d'erreur est proche ou étendu En déduire la proportion et la position de la bande de confiance par rapport à l'intervalle d'équivalence, peut aider à interpréter les résultats au-delà des valeurs de P.