autodiff

Autodiff - Bibliothèque automatique de différenciation C ++

Ce projet a évolué pour augmenter (mathématiques / différenciation / autodiff) et ce référentiel n'est plus mis à jour.

Statut de construction

Bifurquer	Travis	Appyseur	codecov.io
master
develop

Description

Autodiff est une bibliothèque C ++ d'en-tête uniquement qui facilite la différenciation automatique (mode avant) des fonctions mathématiques des variables uniques et multiples.

Cette implémentation est basée sur l'expansion de la série Taylor d'une fonction analytique F au point X₀ :

L'idée essentielle d'Autodiff est la substitution des nombres par des polynômes dans l'évaluation de f (x₀) . En substituant le nombre x₀ par le polynôme de premier ordre x₀ + ε , et en utilisant le même algorithme pour calculer f (x₀ + ε) , le polynôme résultant en ε contient les dérivés de la fonction f '(x₀) , f' '(x₀) , f '' '(x₀) , ... dans les coefficients. Chaque coefficient est égal à la dérivée de son ordre respectif, divisé par le factoriel de l'ordre.

Plus en détail, supposons que l'un est intéressé à calculer les n première dérivés de f à x₀ . Sans perte de précision au calcul des dérivés, tous les termes O (ε ^{n + 1} ) incluent des pouvoirs de ε supérieurs à n peuvent être jetés. (Cela est dû au fait que chaque terme dans un polynôme ne dépend que de termes d'ordre égal et inférieur dans les opérations arithmétiques.) En vertu de ces règles de troncature, F fournit une transformation polynomiale à polynomiale:

La capacité de C ++ à surcharger les opérateurs et les fonctions permet la création d'un fvar de classe qui représente les polynômes dans ε . Ainsi, le même algorithme F qui calcule la valeur numérique de y₀ = f (x₀) , lorsqu'il est écrit pour accepter et retourner les variables d'un type générique (matrice), est également utilisée pour calculer le polynôme ʃ _n y _n εⁿ = f (x₀ + ε) . Les dérivés f ⁽ⁿ⁾ (x₀) sont ensuite trouvés à partir du produit du n factoriel respectif N! et coefficient y _n :

Exemple 1: différenciation à variable unique

 #include <boost / math / différenciation / autodiff.hpp> #include <iostream> modèle <typename t>
T quatrième_power (t const & x) {
  T x4 = x * x;  // retval dans l'opérateur * () utilise la mémoire de X4 via NRVO.
  x4 * = x4;      // Aucune copie de x4 n'est fabriquée dans l'opérateur * = () même lors du carré.
  retour x4;     // x4 utilise la mémoire de Y dans main () via nrvo.} int main () {Utilisation de namespace boost :: math :: différenciation;

  Consxpr Ordre non signé = 5;                  // dérivé d'ordre le plus élevé à calculer.
  auto const x = Make_fvar <double, ordre> (2.0);  // Trouver des dérivés à x = 2.
  auto const y = quatrith_power (x);  pour (non signé i = 0; i <= ordre; ++ i)
    std :: cout << "y.derivative (" << i << ") =" << y.derivative (i) << std :: endl;  retour 0;
} / * Sortie: y.derivative (0) = 16y.derivative (1) = 32y.derivative (2) = 48y.derivative (3) = 48y.derivative (4) = 24y.derivative (5) = 0 * /

Les calcul ci-dessus

Exemple 2: différenciation multi-variable et multi-procision

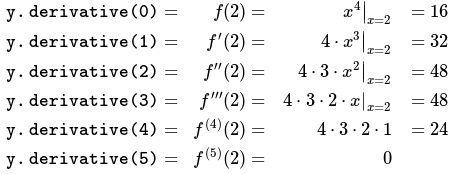
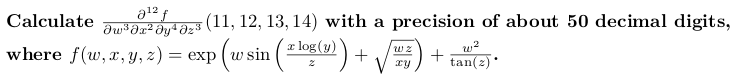
 #include <boost / math / différenciation / autodiff.hpp> #include <boost / multiprecision / cpp_bin_float.hpp> #include <ioStream> en utilisant l'espace de noms boost :: math :: différenciation; modèle <typename w, typename x, typename y, typename z>
promouvoir <w, x, y, z> f (const w & w, const x & x, const y & y, const z & z) {using namespace std;
  return exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z);
} int main () {Utilisation de float50 = boost :: Multiprecision :: cpp_bin_float_50;  constexpr non signé NW = 3;  // Ordre maximum de dérivé à calculer pour w
  constexpr non signé nx = 2;  // Ordre maximum de dérivé à calculer pour x
  constexpr Unsigned NY = 4;  // Ordre maximum de dérivé à calculer pour y
  constexpr Unsigned NZ = 3;  // Ordre maximum de dérivé à calculer pour z
  // Déclarer 4 variables indépendantes ensemble dans un std :: tuple.
  Auto const Variables = Make_ftuple <Float50, NW, NX, NY, NZ> (11, 12, 13, 14);  Auto const & w = std :: get <0> (variables);  // jusqu'aux dérivés NW à w = 11
  Auto const & x = std :: get <1> (variables);  // jusqu'à nx dérivés à x = 12
  Auto const & y = std :: get <2> (variables);  // jusqu'aux dérivés de New York en y = 13
  Auto const & z = std :: get <3> (variables);  // jusqu'aux dérivés nz à z = 14
  Auto const v = f (w, x, y, z);  // calculé à partir de la différenciation symbolique mathématique.
  Float50 const Response ("1976.319600747797717779881875290418720908121189218755");
  std :: cout << std :: setprecision (std :: numérique_limits <fload50> :: chiffres10)
            << "Mathematica:" << Réponse << 'n' << "Autodiff:" << v.derivative (NW, NX, NY, NZ) << 'n' << std :: setPrecision (3)
            << "Erreur relative:" << (v.derivative (NW, NX, NY, NZ) / Réponse - 1) << 'N';  retour 0;
} / * Sortie: Mathematica: 1976.319600747977177798818752904187209081211892188888186.319600747797717779881875290418720908121189218888

Exemple 3: Prix d'option Black-Scholes avec Grecs Calculé automatiquement

 #include <boost / math / différenciation / autodiff.hpp> #include <ioStream> Utilisation de l'espace de noms Boost :: Math :: Constantes; Utilisation de l'espace de noms Boost :: Math :: différenciation; // Les équations et les noms de fonction / variables sont de // https://en.wikipedia.org/wiki/Greeks_(finance)#Formulas_For_European_Option_Greeks// Fonction de distribution cumulative normale standard <typename x>
X phi (x const & x) {return 0.5 * erfc (-one_div_root_two <x> () * x);
} Enum Class CP {appel, put}; // Supposons zéro rendement annuel de dividende (q = 0) .Template <prix typename, typename sigma, typename tau, typename rate>
promouvoir <prix, sigma, tau, tarif> Black_scholes_option_price (CP CP, double k,
                                                            Prix ​​Const & s,
                                                            Sigma Const & Sigma,
                                                            Tau const & tau,
                                                            Rate const & r) {Utilisation de namespace std;
  Auto const d1 = (log (s / k) + (r + sigma * Sigma / 2) * tau) / (Sigma * sqrt (tau));  Auto const d2 = (log (s / k) + (r - Sigma * Sigma / 2) * tau) / (Sigma * sqrt (tau));  switch (cp) {case cp :: call: return s * phi (d1) - exp (-r * tau) * k * phi (d2); case cp :: put: return exp (-r * tau) * k * Phi (-d2) - s * phi (-d1);
  }
} int main () {double const k = 100,0;                    // Prix d'exercice.
  auto const s = Make_fvar <double, 2> (105);  // prix de l'action.
  Double const Sigma = 5;                    // Volatilité.
  Double const tau = 30,0 / 365;             // Il est temps d'expirer depuis des années. (30 jours).
  double const r = 1,25 / 100;               // taux d'intérêt.
  Auto const Call_price = Black_scholes_option_price (cp :: call, k, s, sigma, tau, r);  auto const put_price = Black_scholes_option_price (cp :: put, k, s, sigma, tau, r);

  std :: cout << "Black-Scholes Call Price =" << call_price.derivative (0) << 'n' << "Black-Scholes put prix =" << put_price.derivative (0) << 'n' << "call delta =" << call_price.derivative (1) << 'n' << "put delta =" << put_price.derivative (1) << 'n' << "Call gamma =" << call_price .derivative (2) << 'n' << "put gamma =" << put_price.derivative (2) << 'n';  retour 0;
} / * Sortie: Black-Scholes

Voir Exemple / Black_scholes.cpp pour une plus grande liste d'options Calculées automatiquement Grecs.

Avantages de la différenciation automatique

Les exemples ci-dessus illustrent certains des avantages de l'utilisation d'Autodiff:

• Élimination de la redondance du code. L'existence de n fonctions distinctes pour calculer les dérivés est une forme de redondance du code, avec toutes les responsabilités qui l'accompagnent:

• Les modifications d'une fonction nécessitent n modifications supplémentaires à d'autres fonctions. Dans le 3ème exemple ci-dessus, considérez à quel point la base de code ci-dessus est plus grande et plus dépendante si une fonction distincte était écrite pour chaque valeur grecque.

• Les dépendances sur une fonction dérivée dans un but différent se briseront lorsque des modifications seront apportées à la fonction d'origine. Ce qui n'a pas besoin d'exister ne peut pas se casser.

• Bloat de code, réduisant l'intégrité conceptuelle. Le contrôle de l'évolution du code est plus facile / plus sûr lorsque la base de code est plus petite et peut être saisie intuitivement.

• Précision des dérivés par rapport aux méthodes de différence finie. Les méthodes de différence finie à une seule itération incluent toujours une variable libre Δx qui doit être soigneusement choisie pour chaque application. Si Δx est trop petit, les erreurs numériques deviennent grandes. Si Δx est trop grand, les erreurs mathématiques deviennent grandes. Avec Autodiff, il n'y a pas de variables libres à définir et la précision de la réponse est généralement supérieure aux méthodes de différence finie même avec le meilleur choix de Δx .

Manuel

Des détails supplémentaires figurent dans le manuel Autodiff.

Licence

Distribué sous la licence Software Boost, version 1.0.

Propriétés

• En-tête uniquement.

• Optimisé pour C ++ 17. Compile également et testé avec les normes C ++ 11, C ++ 14 et proposées C ++ 20.

• Toute la mémoire est allouée sur la pile.

Répertoires

Nom	But
doc	documentation
example	exemples
include	têtes
test	tests unitaires

Plus d'informations

• RAPPORT BUGS: Assurez-vous de mentionner la version Boost, la plate-forme et le compilateur que vous utilisez. Un petit échantillon de code compilable pour reproduire le problème est toujours bon également.

• Soumettez vos correctifs comme des demandes de traction contre la branche Develop. Notez qu'en soumettant des correctifs, vous acceptez de concéder à vos modifications sous la licence Boost Software, version 1.0.