6 Nimmt! est un jeu de cartes primé pour deux à dix joueurs de 1994. Citant Wikipedia:
Le jeu a 104 cartes, chacun portant un nombre et un à sept symboles de têtes de taureau qui représentent des points de pénalité. Une série de dix tours est jouée où tous les joueurs placent une carte de leur choix sur la table. Les cartes placées sont organisées sur quatre lignes en fonction des règles fixes. S'il est placé sur une ligne qui a déjà cinq cartes, le joueur reçoit ces cinq cartes, qui comptent comme des points de pénalité qui sont totalisés à la fin du tour.
6 Nimmt! est un jeu compétitif d'informations incomplètes et une grande quantité de stochasticité. Bien jouer nécessite pas mal de planification. Le jeu simultané se prête aux jeux d'esprit et aux bluffs, tandis qu'une stratégie à long terme est nécessaire pour éviter de se retrouver dans des positions de fin de partie difficile.
Nous avons implémenté une version légèrement simplifiée de 6 NIMMT! comme un environnement de gym Openai. Contrairement au jeu d'origine, lors de la lecture d'une carte inférieure que la dernière carte de toutes les piles, le joueur ne peut pas choisir librement la pile à remplacer, mais prendra toujours la pile avec le plus petit nombre de points de pénalité.
Jusqu'à présent, nous avons mis en œuvre les agents suivants:
En tant que premier test, nous avons organisé un tournoi d'auto-play simple. À partir de cinq agents non formés, nous avons joué 4000 matchs au total. Pour chaque jeu, nous avons sélectionné au hasard deux, trois ou quatre agents pour jouer (et apprendre). Tous les 400 jeux, nous avons cloné l'agent le plus performant et avons expulsé certains des plus performants. En fin de compte, nous avons juste gardé la meilleure instance de chaque type d'agent.
Résultats sur tous les jeux:
| Agent | Jeux joués | Score moyen | Gagner la fraction | Elo |
|---|---|---|---|---|
| Alpha0.5 | 2246 | -7,79 | 0,42 | 1806 |
| MCS | 2314 | -8,06 | 0,40 | 1745 |
| Acer | 1408 | -12.28 | 0,18 | 1629 |
| D3qn | 1151 | -13.32 | 0,17 | 1577 |
| Aléatoire | 1382 | -13.49 | 0,19 | 1556 |
C'est ainsi que les performances (mesurées en ELO) des modèles développées au cours du tournoi:
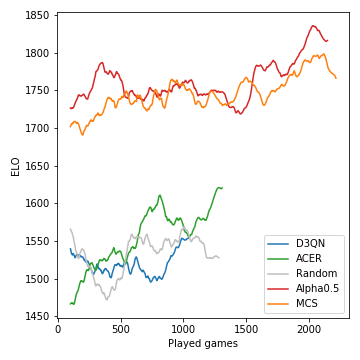
La recherche d'arbres Monte-Carlo est cruciale et mène à des joueurs forts. Les agents RL sans modèle, en revanche, ont du mal à surpasser même clairement la ligne de base aléatoire. En raison de la nature stochastique du jeu, les probabilités de victoire et les différences ELO ne sont pas aussi drastiques qu'elles pourraient l'être, par exemple, pour les échecs. Notez que nous n'avons réglé aucun des nombreux hyperparamètres.
Après cette phase de lecture auto-play, l'agent Alpha0.5 a affronté Merle, l'un des 6 meilleurs Nimmt! joueurs de notre groupe d'amis, pour 5 matchs. Ce sont les scores:
| Jeu | 1 | 2 | 3 | 4 | 5 | Somme |
|---|---|---|---|---|---|---|
| Merle | -10 | -16 | -11 | -3 | -4 | -44 |
| Alpha0.5 | -1 | -3 | -14 | -8 | -6 | -32 |
En supposant que vous avez installé Anaconda, clonez le repo avec
git clone [email protected]:johannbrehmer/rl-6nimmt.git
et créer un environnement virtuel avec
conda env create -f environment.yml
conda activate rl
L'auto-play de l'agent et les jeux entre un joueur humain et des agents formés sont démontrés dans Simple_Tournoi.Ipynb.
Assemblé par Johann Brehmer et Marcel Gutsche.