Les transformations 2D en CSS nous permettent d'effectuer certaines opérations de transformation de base dans un espace bidimensionnel, telles que le déplacement, la rotation, la mise à l'échelle ou la torsion, etc. Les éléments transformés sont similaires aux éléments positionnés de manière absolue et n'affecteront pas les éléments environnants, mais peuvent être combinés. avec Les éléments environnants se chevauchent. La différence est que l'élément converti occupera toujours l'espace avant la conversion sur la page.
Introduisons la conversion 2D :
1. Déplacer la traduction()
Selon les paramètres donnés par les positions gauche (axe X) et supérieure (axe Y), le déplacement à partir de la position actuelle de l'élément peut modifier la position de l'élément sur la page, de la même manière que le positionnement.
1. Grammaire :
transformer: traduire (x, y);
Ou vous pouvez les écrire séparément
transformer:translateX(n);transform:translateY(n);
2. Points clés :
(1) Définir le mouvement dans la transformation 2D et déplacer les éléments le long des axes X et Y ;
(2) Le plus grand avantage de traduire est qu'il n'affectera pas la position des autres éléments ;
(3) Le pourcentage de traduction lui-même est relatif à son propre élément traduire (50 %, 50 %) ;
(4) Cela n'a aucun effet sur les balises en ligne ;
Exemple:
<!DOCTYPEhtml><html><head><style>div{width:100px;height:100px;background-color:#CCC;transform:translate(100px,10px);}</style></head><body ><div></div></body></html>Résultats en cours d'exécution :
2. Rotation rotation()
La méthode rotate() fait pivoter un élément dans le sens des aiguilles d’une montre d’un degré donné. Les valeurs négatives sont autorisées, ce qui entraîne la rotation de l'élément dans le sens inverse des aiguilles d'une montre.
Syntaxe : transfrom:rotate (degré de rotation)
Points clés :
rotation (degré), l'unité est deg. Par exemple : rotation (45deg) ;
Si l'angle est positif, il est dans le sens des aiguilles d'une montre, s'il est négatif, il est dans le sens inverse des aiguilles d'une montre ;
Par défaut, le point central dans le sens des aiguilles d'une montre est le point central de l'élément ;
Exemple:
<!DOCTYPEhtml><html><head><style>div{width:100px;height:100px;background-color:#CCC;margin:20px0px0px20px;transform:rotate(45deg);}</style></head> <corps><div></div></body></html>Résultats en cours d'exécution :
3. Transformation-origine du point central de transformation 2D :
grammaire:
transformation-origine:xy;
Points clés :
(1) Notez que x et y sont séparés par des espaces ;
(2) Le point central par défaut de xy est le point central de l'élément (50 % 50 %) ;
(3) Vous pouvez également définir des pixels ou des noms de direction pour xy (droite, centre, gauche, bas, haut) ;
4. Échelle de zoom()
scale() , la taille de l'élément augmente ou diminue, en fonction des paramètres de largeur (axe X) et de hauteur (axe Y) :
(1) Modifier la taille de l'élément, agrandir ou réduire l'élément
(2) S'il s'agit d'un nombre négatif, il sera inversé.
(3) Le format syntaxique de la fonction est le suivant :
échelle (sx, sy)
Où sx représente le rapport de mise à l'échelle dans la direction horizontale et sy représente le rapport de mise à l'échelle dans la direction verticale. De plus, le paramètre sy peut être omis et sa valeur par défaut est égale à sx.
Exemple:
<!DOCTYPEhtml><html><head><style>div{width:100px;height:100px;background-color:#CCC;transform:scale(0.7);}</style></head><body>< div></div></body></html>Résultats en cours d'exécution :
5. Inclinaison()
Contient deux valeurs de paramètre, indiquant respectivement l'angle d'inclinaison de l'axe X et de l'axe Y. Si le deuxième paramètre est vide, sa valeur par défaut est 0. Un paramètre négatif signifie une inclinaison dans la direction opposée.
(1) skewX(<angle>) signifie une inclinaison uniquement sur l'axe X (direction horizontale).
(2) skewY(<angle>) signifie une inclinaison uniquement dans l'axe Y (direction verticale).
(3) Inclinez les éléments dans différentes directions.
(4) skew(a) est égal à skew(a,0)
(5)inclinaison(x,y)
(6) Angle unitaire en degrés
Exemple:
<!DOCTYPEhtml><html><head><style>div{width:100px;height:100px;background-color:#CCC;margin:20px0px0px10px;transform:skew(-15deg,20deg);}</style>< /head><corps><div></div></body></html>Résultats en cours d'exécution :
6. matrice()
La fonction Matrix() peut être considérée comme l'abréviation de plusieurs fonctions : skew(), scale(), rotate() et Translate(). Toutes les opérations de conversion 2D peuvent être définies en même temps via la fonction Matrix(). le format de syntaxe de la fonction est le suivant :
matrice(a,b,c,d,tx,ty)
Les six paramètres de la fonction Matrix() correspondent respectivement à scaleX(), skewY(), skewX(), scaleY(), TranslateX() et TranslateY(). Vous pouvez utiliser Matrix() pour implémenter diverses opérations de conversion 2D. , tel que:
traduire(tx,ty)=matrix(1,0,0,1,tx,ty);:
où tx et ty sont les valeurs de translation horizontale et verticale ;
rotation(a)=matrix(cos(a),sin(a),-sin(a),cos(a),0,0);
où a est la valeur du degré. Vous pouvez inverser la rotation en échangeant les valeurs sin(a) et -sin(a) ;
échelle(sx,sy)=matrice(sx,0,0,sy,0,0);
où sx et sy sont les valeurs d'échelle horizontale et verticale ;
skew(ax,ay)=matrix(1,tan(ay),tan(ay),1,0,0);
où ax et ay sont les valeurs horizontales et verticales en degrés.
Exemple:
<!DOCTYPEhtml><html><head><style>div{width:100px;height:100px;background-color:#CCC;margin:20px0px0px10px;float:left;}.one{transform:matrix(0.866,0.5, -0.5,0.866,0,0);}.deux{marge-gauche:35px;transform:matrix(0.586,0.8,-0.8,0.686,0,0);}.trois{marge-gauche:40px;marge- top:25px;transform:matrix(0.586,0.8,-0.8,0.866,0,0);}.four{transform:matrix(0.586,0.8,-0.8,0.586,40,30);}</style>< /head><body><divclass=one></div><divclass=two></div><divclass=two></div><divclass=four></div></body></html>Résultats en cours d'exécution :
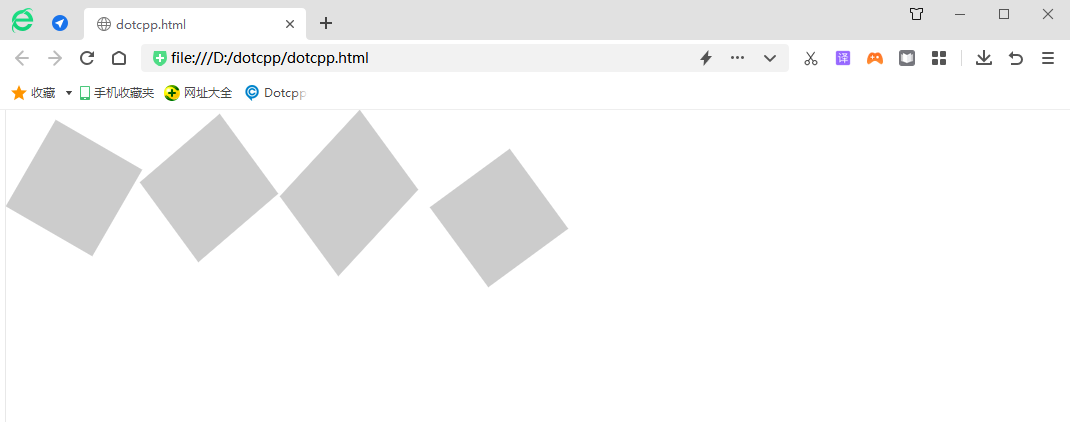
La méthode matrice() et la méthode de transformation 2D sont fusionnées en une seule.
La méthode matricielle comporte six paramètres, dont les fonctions de rotation, de mise à l'échelle, de mouvement (translation) et d'inclinaison.
Utiliser une matrice pour exprimer la matrice du montant de transformation (a,b,c,d,x,y)
●acx
●corps
●0 0 1
Pratiquons-le à partir d’un cas précis :
Le code est le suivant :
<!DOCTYPEhtml><html><head><metacharset=UTF-8><metahttp-equiv=X-UA-Compatiblecontent=IE=edge><metaname=viewportcontent=width=device-width,initial-scale=1.0>< title>Document</title><style>body{margin:100px;}.transformElement{width:200px;height:200px;background-color:red;transition:all1slinear;float:left;position:relative;left:0; color:#FFF;/*transform-origin:lefttop;*/}.transformElement2{width:200px;height:200px;background-color:blue;transition:all1slinear;float:left;}.transformElement:hover{/*transform :translate(200px,0)rotate(360deg)scale(2);*//*left:100px;*//*transform:scale(2,0.5)*/transform:skew(-45deg,45deg);}. horloge{largeur:400px;hauteur:400px;border-radius:50%;background-color:#Faa;position:relative;}.stick{width:4px;height:200px;background-color:blue;position:absolute; gauche : 198 px ; haut : 0 ; transition : all12slinear ; transform-origin : centerbottom ;}.stickshort{width : 8px; :100px;transition:all12slinear;transform-origin:centerbottom;z-index:2;}.clock:hover.stick{transform:rotate(4320deg);}.clock:hover.stickshort{transform:rotate(360deg);} </style></head><body><!--<div></div><div></div>--><div><div></div><div></div>< /div></body></html>Résultats en cours d'exécution :