Artikel ini memberi Anda pengetahuan yang relevan tentang JavaScript, yang terutama memperkenalkan konten relevan tentang tipe angka. Ada dua jenis angka dalam JavaScript: Tipe Number dan BigInt. Mari kita lihat bersama-sama. membantu.
[Rekomendasi terkait: tutorial video javascript, web front-end]
Ada dua jenis angka dalam JavaScript :
Tipe Number , yang merupakan tipe angka dalam pengertian konvensional, disimpan dalam format 64 bit IEEE-754 dan merupakan "angka floating point presisi ganda". Sejauh ini, semua nomor yang pernah kita hubungi adalah dari jenis Number ;
Tipe BigInt mewakili bilangan bulat dengan panjang berapa pun. Biasanya kami tidak menggunakannya kecuali bilangan tersebut mewakili angka selain 2 53 hingga -2 53. Kami akan memperkenalkan tipe data profesional ini secara mendetail di bab selanjutnya;
Cara menulis angka sangat sederhana, tetapi JavaScrpt memiliki banyak gula sintaksis yang mudah dan cepat untuk kita gunakan. Mempelajari gula sintaksis ini tidak hanya akan meningkatkan kemampuan membaca kode kita, tetapi juga meningkatkan pemahaman tingkat tinggi dari kode kita.
Angka desimal adalah yang paling sederhana, dan kita akan menggunakannya kurang lebih di hampir setiap artikel. Misalnya, kita membuat variabel dan menyimpan 100 miliar:
misalkan sepuluh miliar = 10000000000;
Meskipun pengoperasiannya sangat sederhana, namun ada masalah: sulit menghitung berapa 0 yang mengikuti 1 Jika kita menulis kode transfer, angka 0 yang salah dapat menyebabkan kebangkrutan.
Saat ini, kita dapat menggunakan _ sebagai pembatas, sebagai berikut:
misalkan sepuluh miliar = 10_000_000_000;
Kode di atas dapat dengan jelas menghitung jumlah 0 , yang jelas merupakan solusi optimal!
_ bawah di sini adalah gula sintaksis JavaScript , yang akan diabaikan oleh mesin selama eksekusi. Kedua metode penulisan di atas memiliki efek yang sama, tetapi pengalaman membacanya sangat berbeda.
Sirkuit otak Qingqi
Beberapa sepatu anak ada yang bertanya, saya dari kecil selalu berada di kelompok 4 0 , kenapa harus kelompok 3 0 ? Oleh karena itu, kita dapat menulisnya dengan cara berikut tanpa masalah:
misalkan sepuluh miliar = 100_0000_0000;
Atau bisa juga ditulis seperti ini:
misalkan sepuluh miliar = 1_0000_0000_00;
Yang ingin saya ungkapkan di sini adalah metode pembagian apa pun yang Anda gunakan, tidak akan memengaruhi besar kecilnya bilangan itu sendiri.
Meskipun penggunaan _ dapat membagi banyak 0 dengan elegan, dalam kehidupan nyata, kita umumnya tidak menuliskannya seperti ini, misalnya, kita sering menulis 10000000000 sebagai "10 miliar", sehingga banyak 0 yang dapat dihilangkan, sehingga mengurangi kemungkinan pembuatannya. kesalahan.
JavaScript juga menyediakan cara untuk menghilangkan 0 Kita bisa menggunakan huruf e diikuti angka untuk mewakili angka 0 Contoh:
misalkan sepuluh miliar = 1e10;//10 miliar, 1 diikuti 10 0sconsole.log(3.14e9);//3140000000, diikuti 7 0, silakan lihat ke bawah jika ada pertanyaan.
Pemahaman kode di atas sangat sederhana. e10 dapat dipahami sebagai 1_0000_0000_00 0 yaitu 1 diikuti oleh 10 , sehingga kita dapat berpikir:
1e10 === 1 * 1_0000_0000_00;//e10 berarti 1 diikuti 10 03.14e9 === 3.14 * 1_000_000_000;//e9 berarti 1 diikuti 9 0s
Kita juga dapat menggunakan metode ini untuk merepresentasikan bilangan yang sangat kecil, misalnya 1 nanometer:
misalkan nm = 0,000000001; //Satuan (meter)
Karena terlalu banyak 0 , kita juga dapat menggunakan _ :
misalkan nm = 0,000_000_001;
Tentu saja, Anda juga dapat menggunakan e untuk menghilangkan semua 0 , sebagai berikut:
misalkan nm = 1e-9;//9 0s di sebelah kiri 1, termasuk yang sebelum koma desimal
Dengan kata lain, e-9 berarti 1 -9 , yaitu 1/1000_000_000 , sehingga persamaan berikut ini benar:
1e-9 === 1 / 1_000_000_000;3.14e-8 === 3.14 / 1_000_000_00;
Heksadesimal adalah format yang umum digunakan dalam pemrograman, seperti warna, pengkodean, dll. Kita dapat menambahkan 0x sebelum bilangan biasa untuk mewakili bilangan heksadesimal:
misalkan hex = 0xff;//255, tidak peka huruf besar-kecil, 0xFF sama
Bilangan biner dimulai dengan 0b :
biarkan bin = 0b1011;//11
Bilangan oktal dimulai dengan 0o :
misalkan okt = 0o777;//511
Cara penulisan sederhana ini hanya mendukung ketiga tipe khusus ini. Sedangkan untuk bilangan dasar lainnya, Anda dapat menggunakan fungsi khusus untuk menghasilkannya ( parseInt ).
Metode toString dapat mengubah angka menjadi bentuk string yang sesuai dengan base .
Berikan kastanye:
misalkan bilangan = 996; console.log(num.toString(8));//Konversi ke string oktal console.log(num.toString(16));//Konversi ke string heksadesimal console.log(num.toString( 32));// Ubah menjadi 32 string heksadesimal
Hasil eksekusi kodenya adalah sebagai berikut:
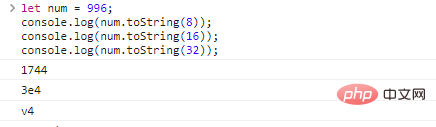
Kisaran base bisa dari 2 hingga 36 Jika tidak diisi, defaultnya adalah 10 .
Perhatikan bahwa jika Anda menggunakan nomor untuk memanggil metode toString secara langsung, dalam beberapa kasus Anda perlu menerapkan dua . misalnya:
console.log(123.toString(8));//Kesalahan, kesalahan sintaksis console.log(123..toString(8));//Benar, 173
Ada dua . setelah angka. Hal ini karena dalam JavaScript . pertama setelah angka dianggap sebagai koma, dan titik kedua adalah .
Jika desimal, masalah ini tidak ada.
konsol.log(3.14.toString(8));
Atau kita bisa menggunakan tanda kurung untuk menghindari penggunaan dua titik, misalnya:
konsol.log((123).toString(8));//'173
Pembulatan adalah salah satu operasi angka yang paling umum dan biasanya mencakup:
Pembulatan ke bawah, Math.floor(num)
console.log(Matematika.lantai(3.14));//3 console.log(Matematika.lantai(9.99));//9 console.log(Matematika.lantai(-3.14));//-4 console.log(Matematika.lantai(-9.99));//-10
Jangan mengikuti prinsip pembulatan dan langsung mengambil bilangan bulat terdekat yang kurang dari atau sama dengan nilai saat ini.
Rangkuman, Math.ceil(num)
konsol.log(Matematika.ceil(3.14));//4 console.log(Matematika.ceil(9.99));//10 console.log(Matematika.ceil(-3.14));//-3 console.log(Matematika.ceil(-9.99));//-9
Jangan mengikuti prinsip pembulatan dan langsung mengambil bilangan bulat terdekat yang lebih besar atau sama dengan bilangan saat ini.
Bulatkan ke bilangan bulat terdekat, Math.round(num)
console.log(Matematika.round(3.14));//3 console.log(Matematika.round(9.99));//10 console.log(Matematika.bulat(-3.14));//-3 console.log(Matematika.bulat(-9.99));//-10
Mengikuti prinsip pembulatan, diambil bilangan bulat terdekat dengan bilangan saat ini.
Hapus desimal, Math.trunc(num)
console.log(Matematika.trunc(3.14));//3 console.log(Matematika.trunc(9.99));//9 console.log(Matematika.trunc(-3.14));//-3 console.log(Matematika.trunc(-9.99));//-9
Hapus langsung angka setelah koma dan bulatkan ke angka bilangan bulat. Browser IE tidak mendukung metode ini
Bandingkan empat metode di atas:
| Matematika.lantai | Matematika.ceil | Matematika.bulat | Matematika.trunc | |
|---|---|---|---|---|
| 3.14 | 3 | 4 | 3 | 3 |
| 9.99 | 9 | 10 | 10 | 9 |
| -3.14 | -4 | -3 | -3 | -3 |
| -9,99 | -10 | -9 | -10 | -9 |
Cara di atas hanya membulatkan desimal menjadi bilangan bulat. Dalam beberapa kasus, kita memerlukan 4 dengan presisi tertentu.
Ada dua metode:
penghitungan perkalian dan pembagian matematika
biarkan pi = 3.1415926;console.log(Matematika.bulat(pi * 10000) / 10000);//3.1416
Kode di atas mengalikan pi terlebih dahulu dengan 10000 , lalu membulatkannya, lalu membaginya dengan 10000 , sehingga diperoleh hasil yang memenuhi syarat akurasi. Namun, ini tampak konyol, dan JavaScript memberi kita cara yang lebih mudah.
untuk Tetap (n)
biarkan pi = 3.1415926;console.log(pi.toFixed(4));//3.1416
Kode di atas sepertinya tidak memiliki masalah dengan outputnya. Faktanya, toFixed + pi.toFixed(4) sebuah string. Jika kita memerlukan tipe numerik, kita perlu mengonversinya.
Selain itu, jika mantissa desimal tidak cukup panjang, toFixed akan menambahkan '0' di akhir:
biarkan num = 3.1;console.log(num.toFixed(9));
Hasil eksekusi kodenya adalah sebagai berikut: 
Ini juga membuktikan bahwa nilai kembalian toFixed adalah string, jika tidak, 0 akan dihilangkan.
Representasi floating point selalu bias dalam banyak kasus
Di dalam komputer, bilangan floating point direpresentasikan sesuai dengan standar IEEE-754 , dimana bilangan floating point presisi tunggal adalah 32 bit dan bilangan floating point presisi ganda adalah 64 bit. Pada bilangan floating point presisi ganda, 1 bit digunakan untuk mewakili tanda, 52 bit digunakan untuk menyimpan angka penting, dan 11 bit digunakan untuk menyimpan posisi koma desimal.
Meski 64 bit sudah bisa mewakili angka yang sangat besar, namun masih ada kemungkinan melewati batas, misalnya:
biarkan bigNum = 1e999;console.log(bigNum);//Infinity
Bilangan yang melebihi nilai maksimalnya akan menjadi Infinity (infinity), sehingga kehilangan besaran bilangan aslinya, yaitu semacam simpangan.
Ada jenis penyimpangan lain yang perlu kita pelajari:
console.log(0.1+0.2 === 0.3);//falseconsole.log(0.1 + 0.2);
Hasil eksekusi kodenya adalah sebagai berikut:
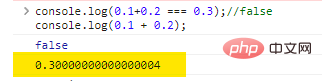
Benar sekali, hasil dari 0.1 + 0.2 bukanlah 0.3 , melainkan sekumpulan 0 yang diikuti oleh 4 .
Penyimpangan seperti ini sangat fatal, terutama pada skenario kerja pusat perbelanjaan dan bank. Bahkan penyimpangan yang sangat kecil pun akan mengakibatkan hilangnya kekayaan yang tiada habisnya dalam skenario perputaran uang yang tinggi.
Saya pernah mendengar cerita tentang seorang pegawai bank yang mencuri jutaan dolar dengan memotong gaji pekerjanya. Gaji setiap pegawai hanya 20 sen!
Saya pikir jika ini terjadi pada saya, saya pasti tidak akan dapat menemukannya, jadi sangat penting untuk selalu akurat.
Saya tidak tahu apakah cerita ini benar atau tidak~~
Mari kita ambil sistem desimal umum kita sebagai contoh. Kita semua tahu bahwa ada dua hal aneh dalam desimal, yang satu disebut desimal berulang tak terhingga, dan yang lainnya disebut 1/3 tak berulang tak terhingga desimal 0.3333333(3) , dan pi Ini adalah desimal tak berulang tak terhingga. Tak terhingga artinya besarnya suatu bilangan tidak dapat digambarkan dengan jelas secara numerik, dan apa yang dapat kita tuliskan tidak akurat.
Ada juga beberapa bilangan perulangan tak terhingga dalam biner. Perbedaannya adalah dalam desimal, bilangan seperti 0.1 yang terlihat sangat sederhana, adalah desimal perulangan tak terhingga dalam biner.
Misalnya:
biarkan x = 0.1;console.log(x.toFixed(20));
Hasil eksekusi kodenya adalah sebagai berikut:
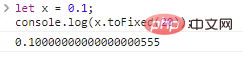
Tidakkah menurut Anda ini luar biasa? Kami hanya membuat variabel dan memberinya nilai 0.1 , lalu mengambil 20 tempat desimal, namun kami mendapatkan hasil yang luar biasa.
Jika kita mengubah sudutnya, fenomena ini mungkin lebih mudah untuk dipahami. Dalam sistem desimal, bilangan bulat apa pun dibagi 10 atau 10 pangkat bilangan bulat adalah bilangan normal dan akurat, seperti 1/10 atau 996/1000 . Namun, jika Anda membaginya dengan 3 , Anda akan mendapatkan hasil perulangan, misalnya 1/3 .
Deskripsi ini juga valid jika dikonversi ke biner.
Dalam biner, bilangan bulat apa pun yang dibagi 2 atau bilangan bulat pangkat 2 adalah bilangan eksak normal. Namun, jika Anda membaginya dengan 10 , Anda akan mendapatkan bilangan biner yang tak terhingga.
Oleh karena itu, kita dapat menyimpulkan bahwa bilangan biner tidak dapat secara akurat mewakili 0.1 dan 0.2 seperti halnya desimal tidak dapat menggambarkan 1/3 .
Melihat:
Penyimpangan data semacam ini bukan merupakan cacat pada JavaScript, melainkan akibat yang sama pada PHP, Java, C, Perl, dan Ruby.
Pembulatan
Saat menampilkan desimal berulang tak terhingga, kita dapat langsung menggunakan metode toFixed untuk membulatkan desimal. Metode ini secara langsung mengembalikan string, yang sangat berguna untuk menampilkan harga.
0.3.toFixed(2);//0.30
Gunakan unit kecil
Cara lainnya adalah kita dapat menggunakan satuan yang lebih kecil untuk menghitung harga dan jarak, seperti menggunakan sen sebagai pengganti yuan untuk menghitung harga total. Faktanya, banyak situs perdagangan yang melakukan hal ini. Namun cara ini hanya mengurangi jumlah kemunculan desimal, dan tidak ada cara untuk sepenuhnya menghindari kemunculan desimal.
Ada dua nilai khusus dalam angka JavaScript : Infinity dan NaN .
Bagaimana cara menilai apakah suatu bilangan merupakan bilangan normal?
Kita dapat menggunakan dua metode:
adalahTerbatas(val)
Fungsi ini akan mengonversi parameter val ke tipe numerik, lalu menentukan apakah bilangan tersebut berhingga, dan mengembalikan true jika bilangan tersebut bukan NaN , Infinity , atau -Infinity .
console.log(isFinite(NaN));//falseconsole.log(isFinite(Infinity));//falseconsole.log(isFinite(3));//trueconsole.log(isFinite('12'));// BENAR Hasil eksekusi kodenya adalah sebagai berikut: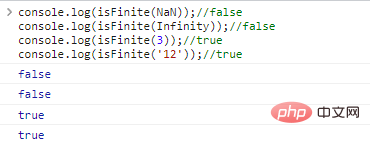
Karena string yang tidak dapat diubah menjadi angka akan diubah menjadi NaN , kita dapat menggunakan metode isFinite untuk menentukan apakah string tersebut merupakan string numerik:
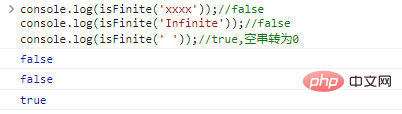
console.log(isFinite('xxxx'));//falseconsole.log(isFinite('Infinite'));//falseconsole.log(isFinite(' '));//true, string kosong diubah menjadi 0Hasil eksekusi kodenya adalah sebagai berikut:
adalahNaN(val)
Mengembalikan true ketika val adalah NaN atau nilai lain yang tidak dapat dikonversi menjadi angka.
console.log(isNaN(NaN));//trueconsole.log(isNaN('Tak Terbatas'));//true Hasil eksekusi kode: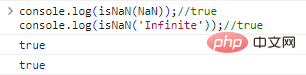
Mengapa menggunakan fungsi isNaN daripada membacanya secara langsung?
Misalnya:
konsol.log(NaN === NaN);//false
Hasil eksekusi kodenya adalah sebagai berikut:
Hal ini karena NaN tidak sama dengan bilangan apapun, termasuk bilangan itu sendiri.
Object.is(a,b) dapat menentukan apakah parameter a dan b sama. Jika sama, ia akan mengembalikan true , jika tidak, ia akan mengembalikan false .
Dapat dibandingkan dengan NaN
console.log(Object.is(NaN,NaN));//true
Hasil eksekusi kode:

0 dan -0
console.log(Object.is(0,-0));//false
Hasil eksekusi kode:

Di dalam komputer, positif dan negatif dilambangkan dengan 0 dan 1 Karena tanda yang berbeda, 0 dan -0 sebenarnya berbeda, dan dinyatakan dengan cara yang berbeda.
lainnya
Situasi perbandingan lainnya sama persis dengan a === b .
parseInt dan parseFloat dapat mengubah string menjadi angka. Tidak seperti + dan Number , batasannya lebih longgar. Misalnya, menggunakan + dan Number untuk string seperti "100¥" pasti akan mengembalikan NaN , tetapi parseInt dan parseFloat dapat menanganinya dengan mudah.
Misalnya:
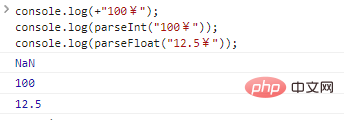
console.log(+"100¥");console.log(parseInt("100¥"));console.log(parseFloat("12.5¥"));Hasil eksekusi kode:
parseInt dan parseFloat membaca angka dari sebuah string hingga tidak dapat dibaca lagi. Keduanya sangat cocok untuk memproses string yang dimulai dengan angka seperti "99px" dan "11.4em" , tetapi NaN dikembalikan untuk string yang dimulai dengan karakter lain.
konsol.log(parseInt('ff2000'));//NaN Namun, kami menemukan ff2000 sebenarnya adalah string digital heksadesimal. parseInt juga dapat menangani situasi ini, tetapi perlu menambahkan parameter heksadesimal.
Misalnya:
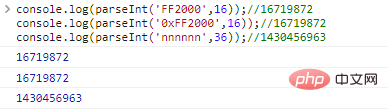
konsol.log(parseInt('FF2000',16));
//16719872
konsol.log(parseInt('0xFF2000',16));
//16719872
console.log(parseInt('nnnnnn',36));
//1430456963Hasil eksekusi kode:
Objek Math bawaan berisi banyak konstanta dan metode yang sering kita gunakan. Berikut adalah beberapa contoh yang umum digunakan:
Matematika.PI
Pi Π adalah konstanta non-siklik tak terhingga, kita dapat menggunakan Math.PI sebagai gantinya:
console.log(Matematika.PI);

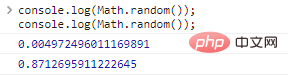
Matematika.acak()
Hasilkan nomor acak dalam interval [0,1) :
console.log(Matematika.acak());konsol.log(Matematika.acak());
Jika kita membutuhkan bilangan acak dalam rentang tertentu, kita dapat mengalikannya dengan nilai tertentu lalu membulatkannya.
Matematika.pow(a,b)
Hitung a b , misalnya:
console.log(Matematika.pow(2,3));//8
Matematika.max()/Matematika.min()
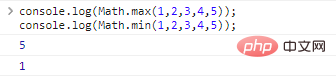
Pilih nilai maksimum/minimum dari sejumlah argumen:
console.log(Math.max(1,2,3,4,5));//5console.log(Math.min(1,2,3,4,5));//1