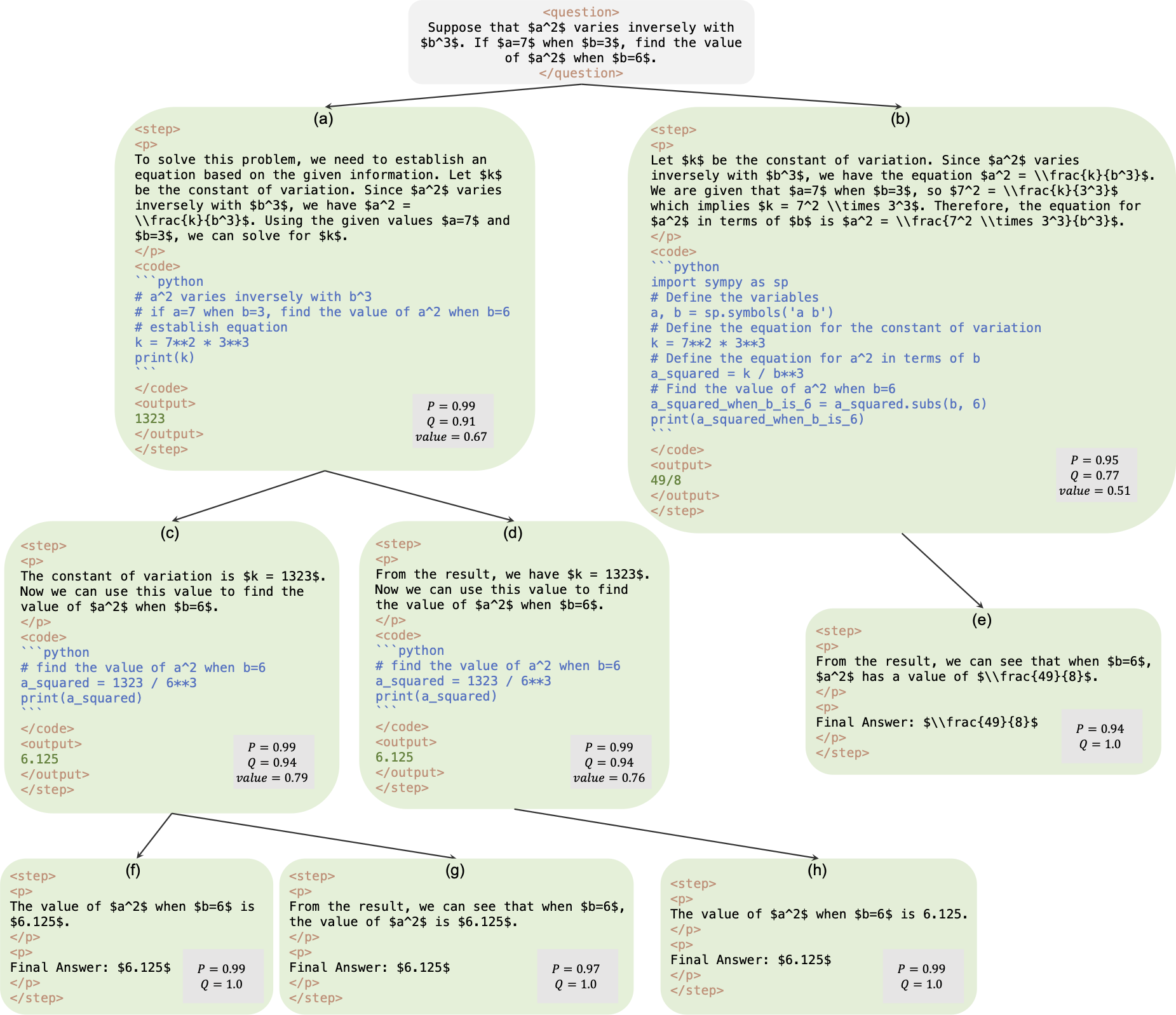
これは、論文 AlphaMath ほぼゼロ: プロセスなしのプロセス監視の公式リポジトリです。コードは社内コードベースから抽出されています。その結果、論文で報告された数値を再現する際にわずかな違いが生じる可能性がありますが、それらは非常に近いものとなるはずです。私たちのアプローチには、Monte Carlo Tree Search (MCTS) フレームワークから派生した数学的推論のみを使用してポリシーと価値のモデルをトレーニングすることが含まれており、GPT-4 や人間によるアノテーションの必要性が排除されています。これは、ラウンド 3 で MCTS によって生成されたトレーニング インスタンスの図です。
チェックポイント: AlphaMath-7B ラウンド 3 ? / AlphaMath-7B ラウンド 3 ?
データセット: AlphaMath-Round3-Trainset ?トレーニング データの解決プロセスは、ラウンド 2 の MCTS とチェックポイントに基づいて自動的に生成されます。ポリシーと価値モデルのトレーニングには、肯定的な例と否定的な例の両方が含まれています。
トレーニング コード: ポリシーにより、一部の主要な機能の実装の詳細のみを公開できます。これらの機能は基本的に独自のトレーニング コードで変更する必要があります。
| 推論方法 | 正確さ | 平均qあたりの時間(秒) | 平均ステップ | #ソル |
|---|---|---|---|---|
| よく深い | 53.62 | 1.6 | 3.1 | 1 |
| 少佐@5 | 61.84 | 2.9 | 2.9 | 5 |
| ステップレベルビーム (1,5) | 62.32 | 3.1 | 3.0 | トップ1 |
| 5 ラン + Maj@5 | 67.04 | ×5 | ×1 | 5トップ1 |
| ステップレベルビーム (2,5) | 64.66 | 2.4 | 2.4 | トップ1 |
| ステップレベルビーム (3,5) | 65.74 | 2.3 | 2.2 | トップ1 |
| ステップレベルビーム (5,5) | 65.98 | 4.7 | 2.3 | トップ1 |
| 1 ラン + Maj@5 | 66.54 | ×1 | ×1 | トップ5 |
| 5 ラン + Maj@5 | 69.94 | ×5 | ×1 | 5トップ1 |
| MCTS (N=40) | 64.02 | 10.1 | 3.8 | トップ1 |
+ Maj@5 5 回実行する必要があるため、多様性が促進されます。+ Maj@5 5 つの候補を直接使用するため、多様性に欠けます。| 温度 | 0.6 | 1.0 |
|---|---|---|
| ステップレベルビーム (1,5) | 62.32 | 62.76 |
| ステップレベルビーム (2,5) | 64.66 | 65.60 |
| ステップレベルビーム (3,5) | 65.74 | 66.28 |
| ステップレベルビーム (5,5) | 65.98 | 66.38 |
ステップレベルのビーム検索では、 temperature=1.0に設定すると、わずかに良い結果が得られる場合があります。
requirements.txt pip install -r requirements.txt
または単にコマンドに従ってください
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py使用して、LLM に値 head を追加できます。 次の 2 つのコマンドのいずれかを実行できます。両者の間には若干の精度の違いがある可能性があります。私たちのマシンでは、最初の結果は 53.4%、2 番目の結果は 53.62% でした。
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
または
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
私たちのマシンの MATH テストセットでは、構成B1=1, B2=5の次の cmd は最大 62% を達成でき、構成B1=3, B2=5のコマンドは最大 65% に達します。
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
精度を計算する
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
ground_truth (解決プロセスではなく、最終的な答え) は、 qaf json または jsonl ファイルで提供する必要があります (形式例は../MARIO_EVAL/data/math_testset_annotation.jsonを参照できます)。
ラウンド1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
丸め > 1、SFT 後
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
解の生成にはquestionのみが使用されますが、精度の計算にはground_truthが使用されます。
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
ステップレベルのビーム検索とは異なり、最初に完全なツリーを構築し、次に MCTS をオフラインで実行して精度を計算する必要があります。
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
注: この評価スクリプトは、ステップレベルのビーム検索によって保存されたツリーで実行することもでき、精度は同じままです。
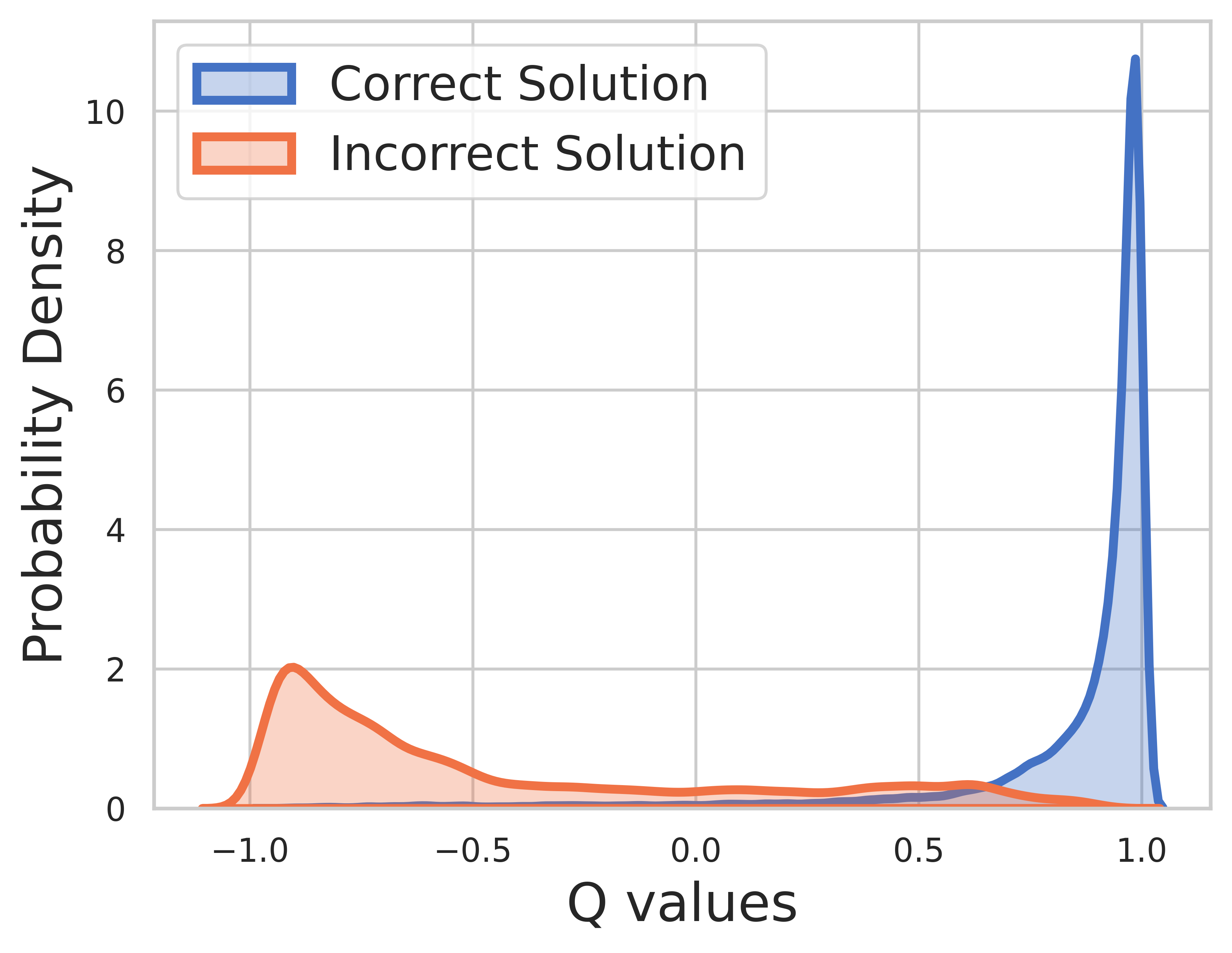
トレーニング データのグラウンド トゥルースは既知であるため、最終ステップの値は報酬であり、Q 値は非常によく収束します。
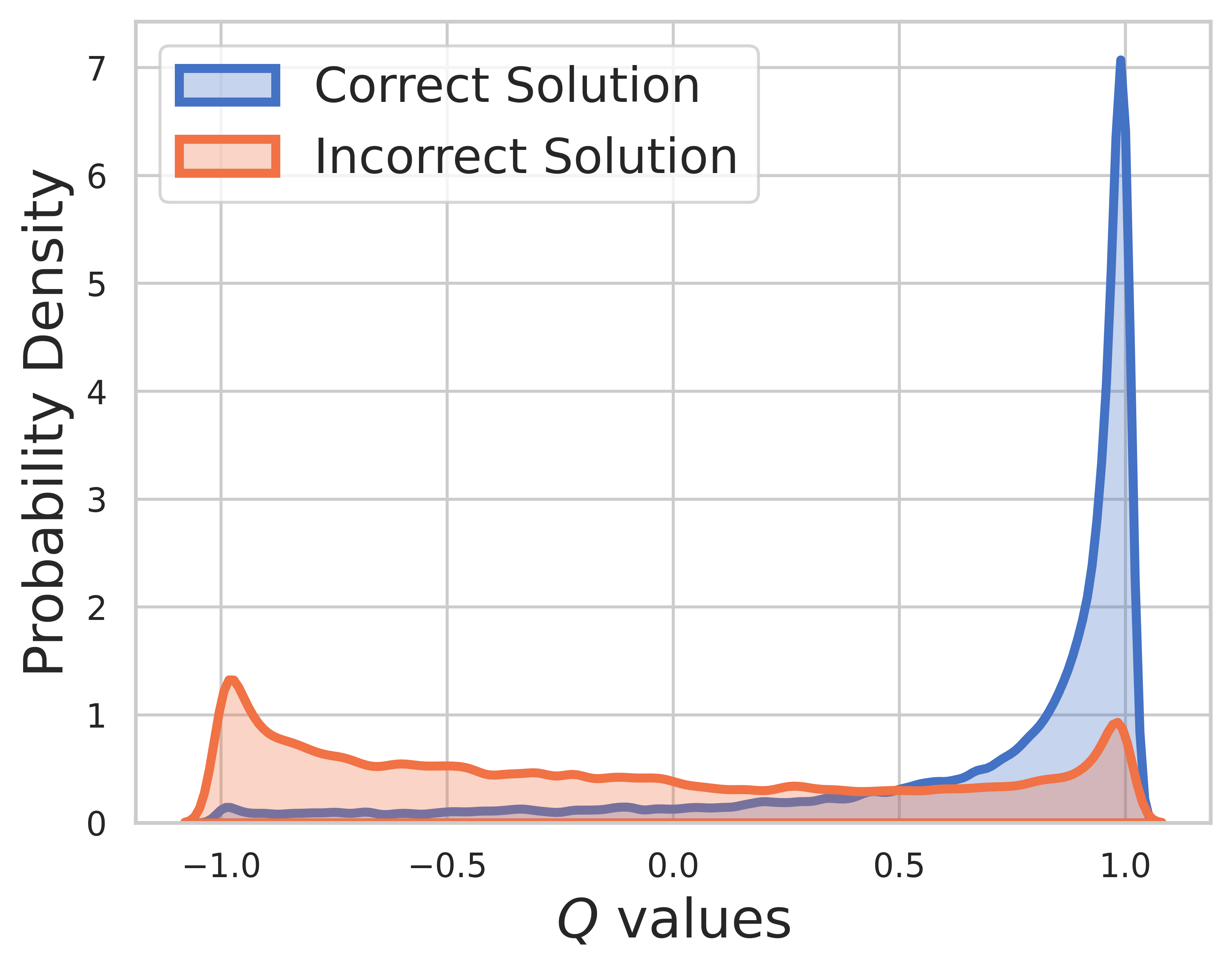
テスト セットでは、グランド トゥルースは不明であるため、Q 値の分布には中間ステップと最終ステップの両方が含まれます。この図からわかることは、
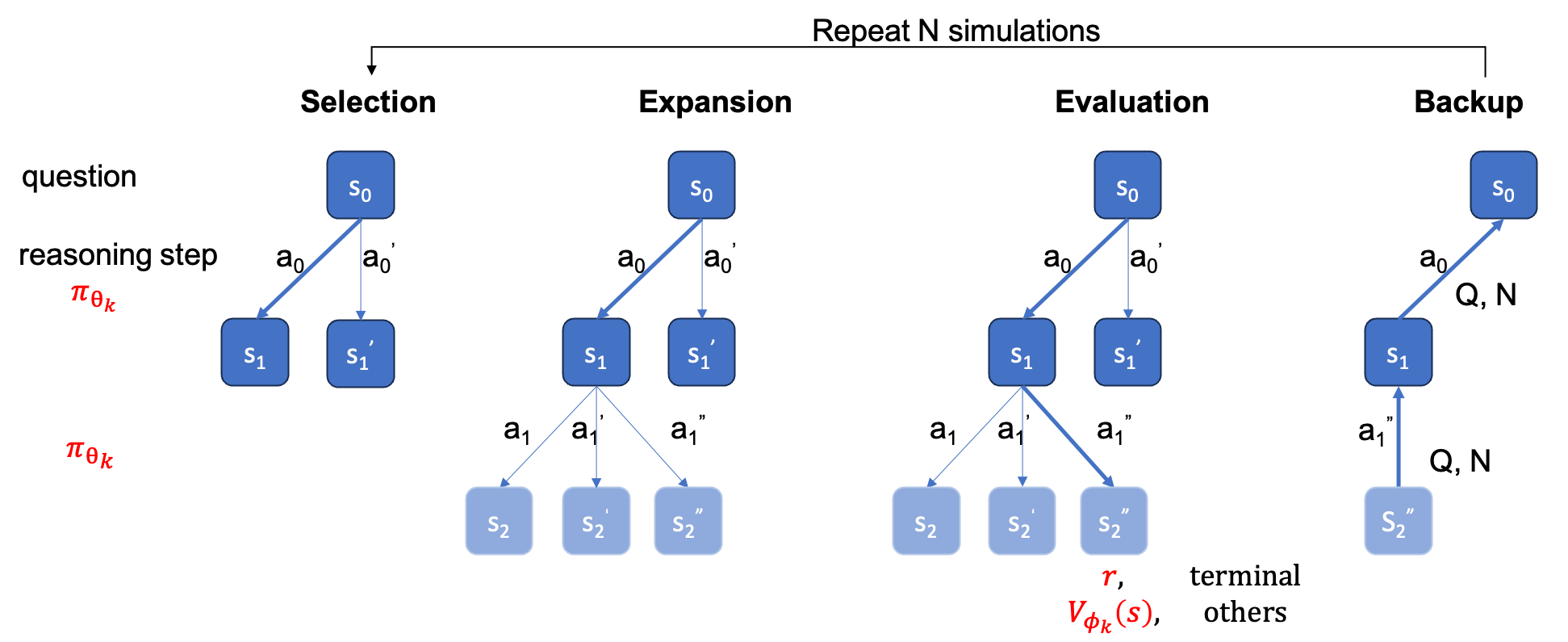
MCTSによるSVPO
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
MCTSバージョン
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
評価ツールキット
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
OVM (成果価値モデル) バージョン
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}