Lanczos (ランチョスと発音) リサンプリングは、デジタル信号を補間するための高度な技術であり、最近傍補間や双線形補間などの単純な方法と比較して優れた画質を提供します。ディテールを効果的に保存し、エイリアシングアーチファクトを最小限に抑えることにより、Lanczos リサンプリングは画像および信号処理アプリケーションで広く使用されています。
Lanczos は画質に優れていますが、その代償として計算の複雑さが増大します。さらに、特に鋭いエッジの周囲で「リンギング」アーティファクトが発生する可能性が欠点になる可能性があります。これらの課題にもかかわらず、Lanczos は全体的なパフォーマンス上の利点により、画像の拡大縮小や回転などのタスクには依然として推奨されています。
このドキュメントでは、理論的基礎、実装の詳細、実際のアプリケーションなど、Lanczos リサンプリングの包括的な概要を説明します。この強力な手法を理解して活用しようとしている開発者や研究者にとって、貴重なリソースとして役立ちます。以降のセクションでは、Lanczos カーネル、補間およびリサンプリング プロセス、フラックス保存、アップサンプリング、ダウンサンプリング、サンプル位置決め、出力範囲、多次元補間、分離可能性など、Lanczos リサンプリングの重要な側面を詳しく掘り下げます。ソースコードを伴う実践的な例が含まれています。
Lanczos カーネルは、特定のサポート サイズに対して定義され、Lanczos リサンプリングで使用される関数です。カーネルは次のように定義されます。
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
どこ:
正規化された sinc 関数は次のように定義されます。
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
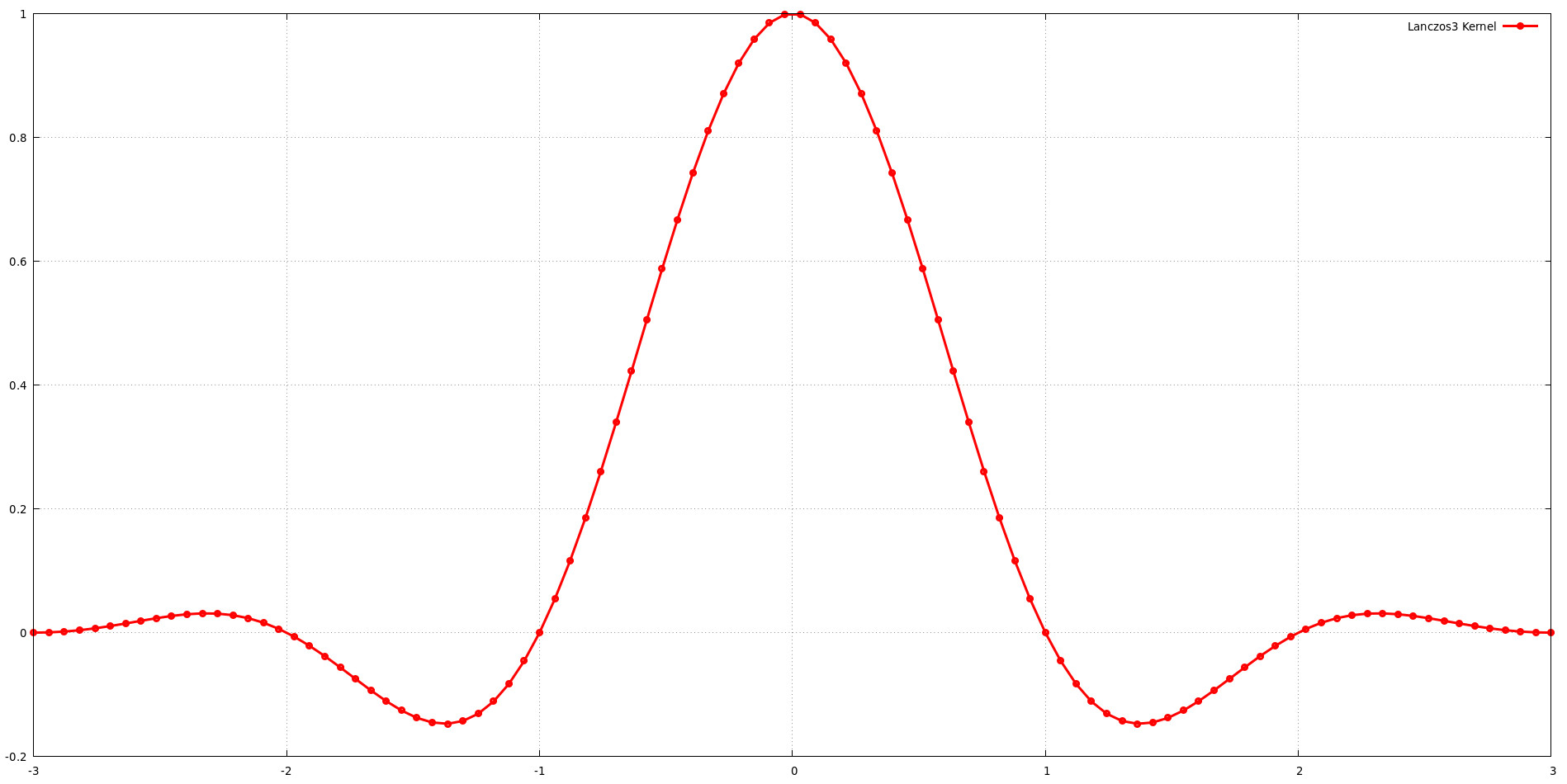
このグラフは、サポート サイズ a = 3 のランチョス カーネルの形状を示しています。これは、カーネルに sinc 関数の 3 つのローブが含まれていることを意味します。サポート サイズ (a) を増やすと、一般に周波数応答を形成する際の柔軟性が高まりますが、計算コストも増加します。サポート サイズを選択するときは、画質と計算効率のバランスを取る必要があります。 a = 3 の Lanczos カーネルが低周波の保存と高周波の除去の優れたバランスを提供するという Jim Blinn の発見は、この概念を裏付けています。
注: 「カーネル幅」、「サポート サイズ」、および「フィルター サイズ」という用語は、パラメーター a を説明するために同じ意味で使用されることがよくあります。ただし、Lanczos リサンプリングのコンテキストでは、「サポート サイズ」が概念を最も正確に反映します。
ランチョス補間は、離散信号を新しいサンプリング レートにリサンプリングするために使用される手法です。これは、元の信号を Lanczos カーネルで畳み込むことによって実現されます。
補間信号 s2(x) は次のように計算できます。
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
どこ:
フラックスの保持:
正規化係数 w(x) は、補間プロセス中に信号全体のエネルギーまたは質量を保存するために重要です。これにより、補間された値の合計が元のサンプルの合計に近似することが保証されます。フィルターの重みは次のように計算されます。
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
アップサンプリング:
サンプリング レートを上げる場合、Lanczos 補間式を変更せずに直接使用できます。
ダウンサンプリング:
サンプリング レートを下げるときにエイリアシング アーティファクトが発生しないようにするには、新しいサンプリング レートに一致するようにフィルタ スケールを調整する必要があります。
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
どこ:
信号を n1 サンプルから n2 サンプルにリサンプリングする場合、次のサンプル位置が使用されます。インデックス j は、サンプリングされた信号 s2(x) からのサンプルを表すために使用されます。 (j + 0.5) の項は、s2(x) のサンプルの中心です。このステップでは、s2(x) の点を s1(x) の点にスケールします。 x の最後の -0.5 項は、ランチョス係数サンプルのオフセットを引き起こす位相シフトです。
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
ランチョス補間を実行するときは、信号境界に特別な注意を払う必要があります。一般的なエッジ処理テクニックには次のものがあります。
ゼロパディング:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
クランプ:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
クランプは、エッジ近くの鋭い不連続性によって引き起こされるエッジアーチファクトを軽減するため、多くの場合好まれます。ただし、エッジ処理方法の選択は、特定のアプリケーションと必要な出力によって異なります。
L(x) のローブにより、s2(x) の範囲は s1(x) の範囲よりも大きくなる場合があります。たとえば、[0.0,1.0] の範囲のピクセル カラーに対応する入力信号 s1(x) は、[0,255] の符号なしバイトに変換し直したときに出力値がオーバーフローしないように、同じ範囲にクランプする必要があります。 。
Lanczos カーネルを複数の次元に拡張して、画像または高次元データに対して補間を実行できます。
2 次元の Lanczos カーネルは次のように定義されます。
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
内挿信号 s2(x, y) は、次の式を使用して計算できます。
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
ここで、w(x, y) は、2 次元 Lanczos カーネルを使用して計算された正規化係数です。
一部の内挿方法とは異なり、Lanczos カーネルは分離不可能です。つまり、1 次元カーネルの積に因数分解することができません。この特性により、通常、分離可能なカーネルと比較して計算コストが高くなります。パフォーマンスを向上させるために、一部の実装では、水平方向と垂直方向の次元に個別のパスを実行することで Lanczos カーネルを近似します。
水平補間:
垂直補間:
数学的表現:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
正規化係数 w(x) と w(y) は 1 次元 Lanczos カーネルを使用して計算されることに注意してください。
重要なポイント:
同様に、テクスチャ ミップマップを生成するために一般的に行われるように、信号を複数回再帰的にリサンプリングすると、各リサンプリング ステップでの誤差が蓄積するため、画質が低下する可能性があります。
lancos-test サンプルを実行し、gnuplot を使用して、Lanczos リサンプリングが 2 倍にアップサンプリングおよびダウンサンプリングされたときに単純な 1 次元信号にどのような影響を与えるかを確認します。
make
./lanczos-test
gnuplot
> load "output.plot"
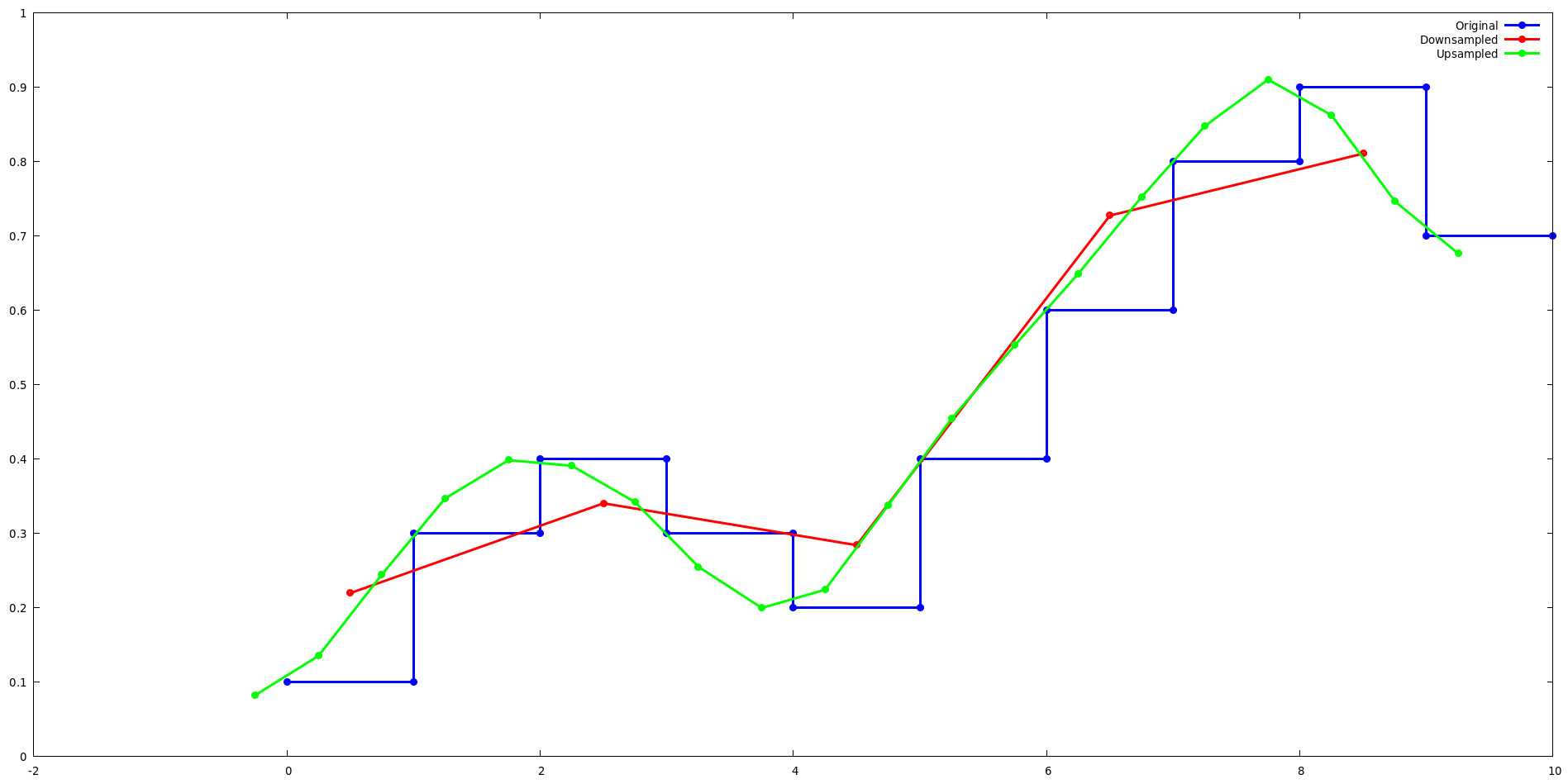
アップサンプリング:
2 のべき乗でアップサンプリングする場合、Lanczos カーネルは 2^ レベルの値セットの間を循環します。たとえば、lanzcos-test アップサンプル例の最初の 4 つの出力を考えてみましょう。 L(x) の出力が j={0,2} と j={1,3} で繰り返されることに注意してください。
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
ダウンサンプリング:
2 のべき乗でダウンサンプリングすると、(x - Floor(x)) が位相シフトに一致する定数になるため、ランチョス カーネルは x から独立します。たとえば、lanzcos-test ダウンサンプル例の最初の 2 つの出力を考えてみましょう。 L(x) の出力が j ごとに繰り返されることに注意してください。
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
さらなる最適化として、これらのケースに対して Lanczos カーネルを事前計算して、高価な sinc 関数の計算を排除することができます。
この README は Google Gemini の協力を得て作成されました。
追加の参考文献には次のものがあります。
このコードは、MIT ライセンスに基づいて Jeff Boody によって実装されました。
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.