このファイルでは、一度に 1 つのテンソルと行列の乗算を最初から実装しました。
また、メタが llama3 に提供したモデル ファイルからテンソルを直接ロードするつもりなので、このファイルを実行する前に重みをダウンロードする必要があります。ウェイトをダウンロードするための公式リンクは次のとおりです: https://llama.meta.com/llama-downloads/
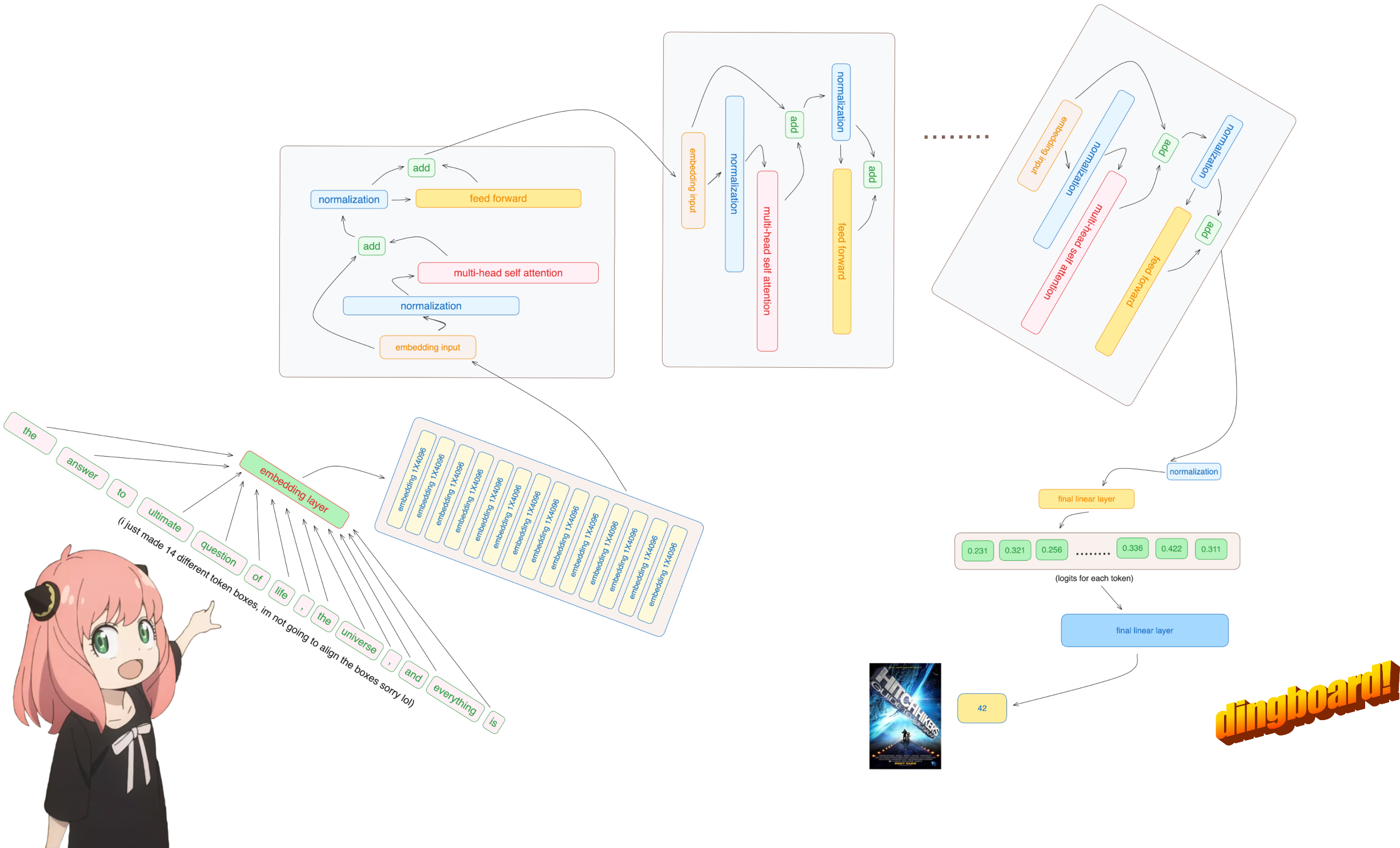
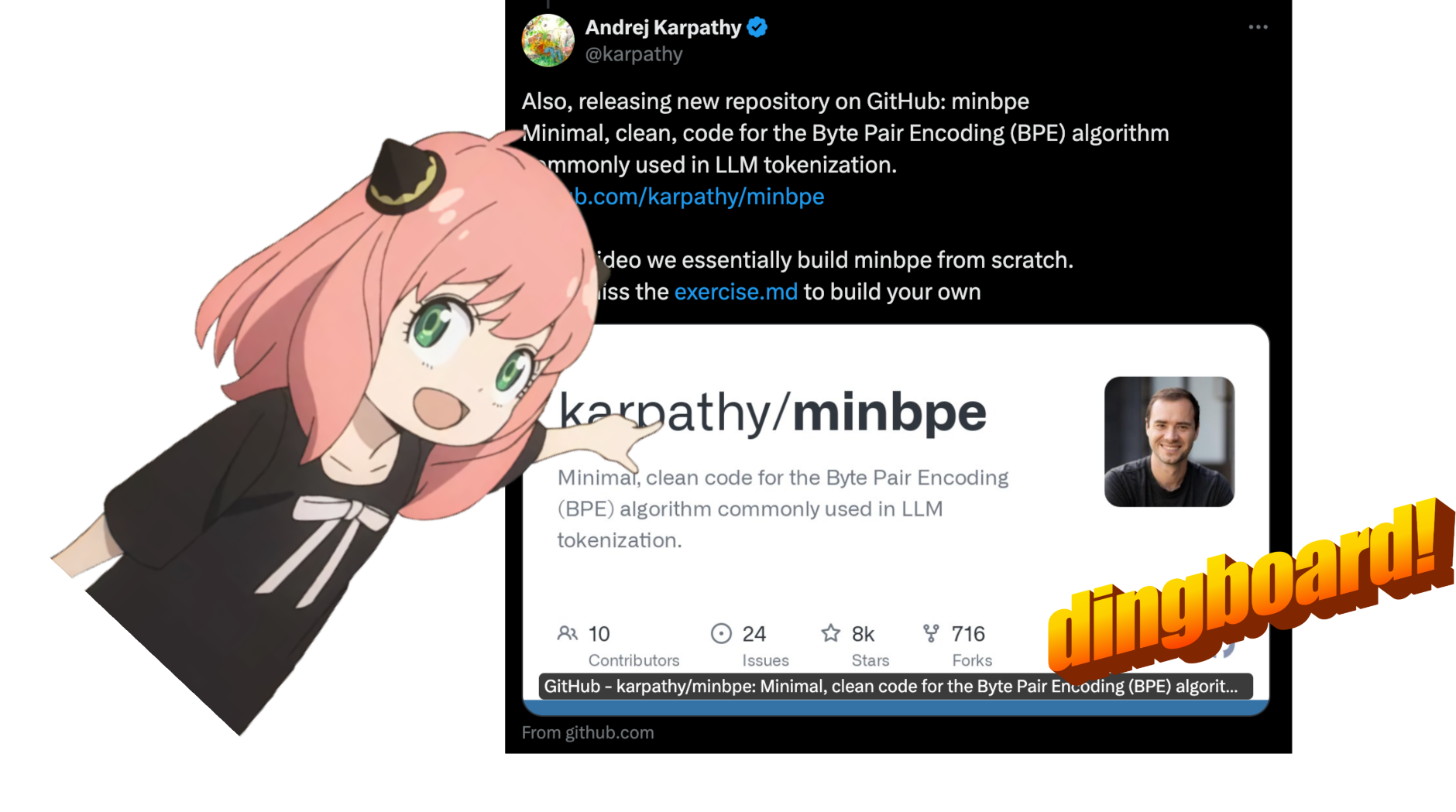
私は bpe トークナイザーを実装するつもりはありません (しかし、andrej karpathy は非常にクリーンな実装を持っています)
彼の実装へのリンク: https://github.com/karpathy/minbpe
from pathlib import Path
import tiktoken
from tiktoken . load import load_tiktoken_bpe
import torch
import json
import matplotlib . pyplot as plt
tokenizer_path = "Meta-Llama-3-8B/tokenizer.model"
special_tokens = [
"<|begin_of_text|>" ,
"<|end_of_text|>" ,
"<|reserved_special_token_0|>" ,
"<|reserved_special_token_1|>" ,
"<|reserved_special_token_2|>" ,
"<|reserved_special_token_3|>" ,
"<|start_header_id|>" ,
"<|end_header_id|>" ,
"<|reserved_special_token_4|>" ,
"<|eot_id|>" , # end of turn
] + [ f"<|reserved_special_token_ { i } |>" for i in range ( 5 , 256 - 5 )]
mergeable_ranks = load_tiktoken_bpe ( tokenizer_path )
tokenizer = tiktoken . Encoding (
name = Path ( tokenizer_path ). name ,
pat_str = r"(?i:'s|'t|'re|'ve|'m|'ll|'d)|[^rnp{L}p{N}]?p{L}+|p{N}{1,3}| ?[^sp{L}p{N}]+[rn]*|s*[rn]+|s+(?!S)|s+" ,
mergeable_ranks = mergeable_ranks ,
special_tokens = { token : len ( mergeable_ranks ) + i for i , token in enumerate ( special_tokens )},
)
tokenizer . decode ( tokenizer . encode ( "hello world!" )) 'hello world!'
通常、これを読み取るかどうかは、モデル クラスの記述方法とその内部の変数名によって異なります。
しかし、私たちは llama3 を最初から実装しているので、一度に 1 つのテンソルずつファイルを読み取ります。
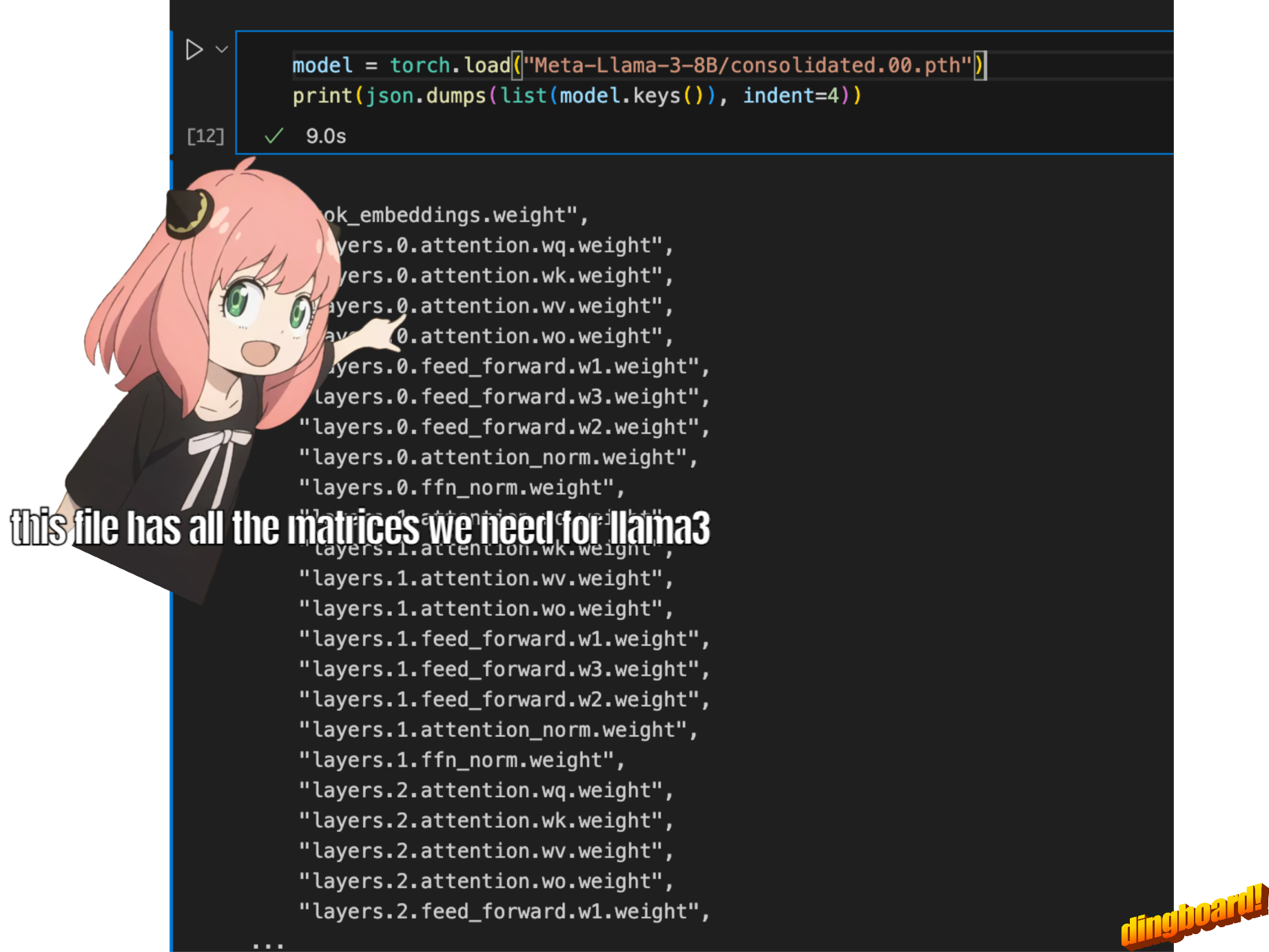
model = torch . load ( "Meta-Llama-3-8B/consolidated.00.pth" )
print ( json . dumps ( list ( model . keys ())[: 20 ], indent = 4 )) [
"tok_embeddings.weight",
"layers.0.attention.wq.weight",
"layers.0.attention.wk.weight",
"layers.0.attention.wv.weight",
"layers.0.attention.wo.weight",
"layers.0.feed_forward.w1.weight",
"layers.0.feed_forward.w3.weight",
"layers.0.feed_forward.w2.weight",
"layers.0.attention_norm.weight",
"layers.0.ffn_norm.weight",
"layers.1.attention.wq.weight",
"layers.1.attention.wk.weight",
"layers.1.attention.wv.weight",
"layers.1.attention.wo.weight",
"layers.1.feed_forward.w1.weight",
"layers.1.feed_forward.w3.weight",
"layers.1.feed_forward.w2.weight",
"layers.1.attention_norm.weight",
"layers.1.ffn_norm.weight",
"layers.2.attention.wq.weight"
]
with open ( "Meta-Llama-3-8B/params.json" , "r" ) as f :
config = json . load ( f )
config {'dim': 4096,
'n_layers': 32,
'n_heads': 32,
'n_kv_heads': 8,
'vocab_size': 128256,
'multiple_of': 1024,
'ffn_dim_multiplier': 1.3,
'norm_eps': 1e-05,
'rope_theta': 500000.0}
dim = config [ "dim" ]
n_layers = config [ "n_layers" ]
n_heads = config [ "n_heads" ]
n_kv_heads = config [ "n_kv_heads" ]
vocab_size = config [ "vocab_size" ]
multiple_of = config [ "multiple_of" ]
ffn_dim_multiplier = config [ "ffn_dim_multiplier" ]
norm_eps = config [ "norm_eps" ]
rope_theta = torch . tensor ( config [ "rope_theta" ])ここではトークナイザーとして tiktoken (openai ライブラリだと思います) を使用します
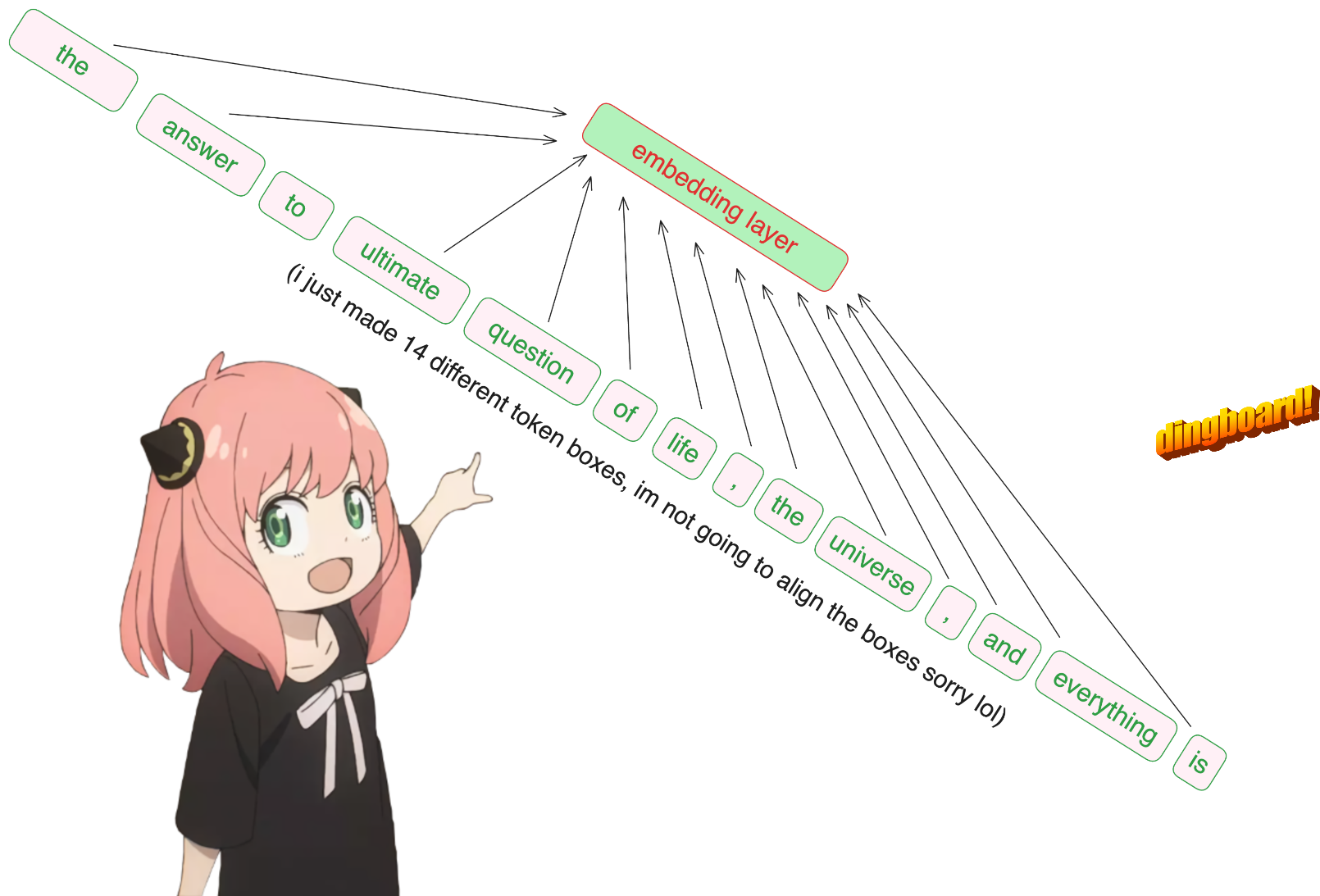
prompt = "the answer to the ultimate question of life, the universe, and everything is "
tokens = [ 128000 ] + tokenizer . encode ( prompt )
print ( tokens )
tokens = torch . tensor ( tokens )
prompt_split_as_tokens = [ tokenizer . decode ([ token . item ()]) for token in tokens ]
print ( prompt_split_as_tokens ) [128000, 1820, 4320, 311, 279, 17139, 3488, 315, 2324, 11, 279, 15861, 11, 323, 4395, 374, 220]
['<|begin_of_text|>', 'the', ' answer', ' to', ' the', ' ultimate', ' question', ' of', ' life', ',', ' the', ' universe', ',', ' and', ' everything', ' is', ' ']
申し訳ありませんが、コードベースで組み込みのニューラル ネットワーク モジュールを使用しているのはこれだけです
とにかく、[17x1] トークンは [17x4096]、つまり長さ 4096 の 17 個の埋め込み (トークンごとに 1 つ) になりました。
注: 形状を記録しておくと、すべてを理解しやすくなります。

embedding_layer = torch . nn . Embedding ( vocab_size , dim )
embedding_layer . weight . data . copy_ ( model [ "tok_embeddings.weight" ])
token_embeddings_unnormalized = embedding_layer ( tokens ). to ( torch . bfloat16 )
token_embeddings_unnormalized . shape torch.Size([17, 4096])
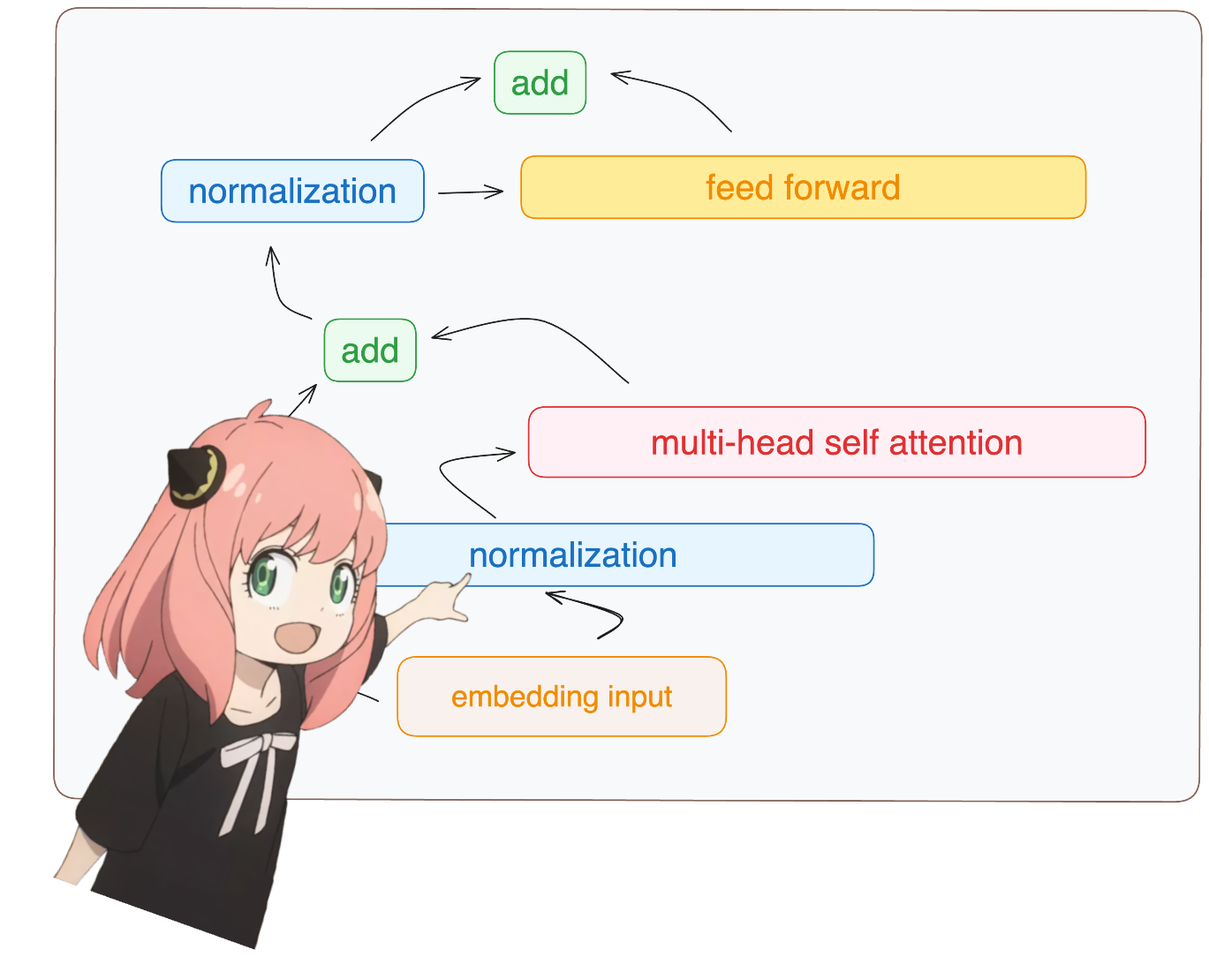
このステップの後、形状は変化せず、値が正規化されただけであることに注意してください。
覚えておくべきことは、rms を誤って 0 に設定して 0 で割ることを避けるため、(設定からの) Norm_eps が必要であるということです。
式は次のとおりです。

# def rms_norm(tensor, norm_weights):
# rms = (tensor.pow(2).mean(-1, keepdim=True) + norm_eps)**0.5
# return tensor * (norm_weights / rms)
def rms_norm ( tensor , norm_weights ):
return ( tensor * torch . rsqrt ( tensor . pow ( 2 ). mean ( - 1 , keepdim = True ) + norm_eps )) * norm_weightsモデル辞書からlayer.0にアクセスしているのがわかります(これが最初の層です)
とにかく、正規化した後も形状は埋め込みと同じ [17x4096] ですが、正規化されています。
token_embeddings = rms_norm ( token_embeddings_unnormalized , model [ "layers.0.attention_norm.weight" ])
token_embeddings . shape torch.Size([17, 4096])
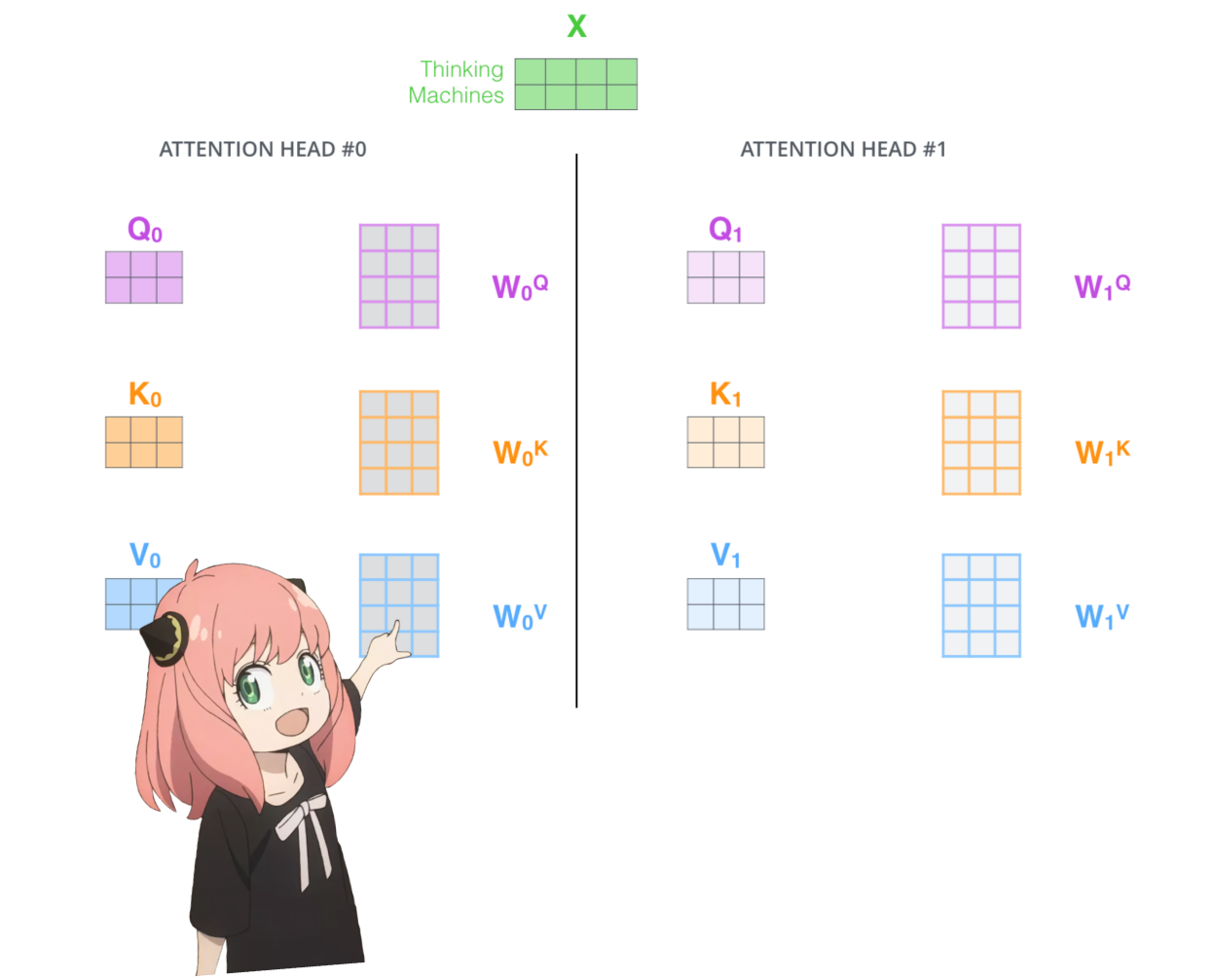
トランスフォーマーの最初の層のアテンションヘッドをロードしましょう
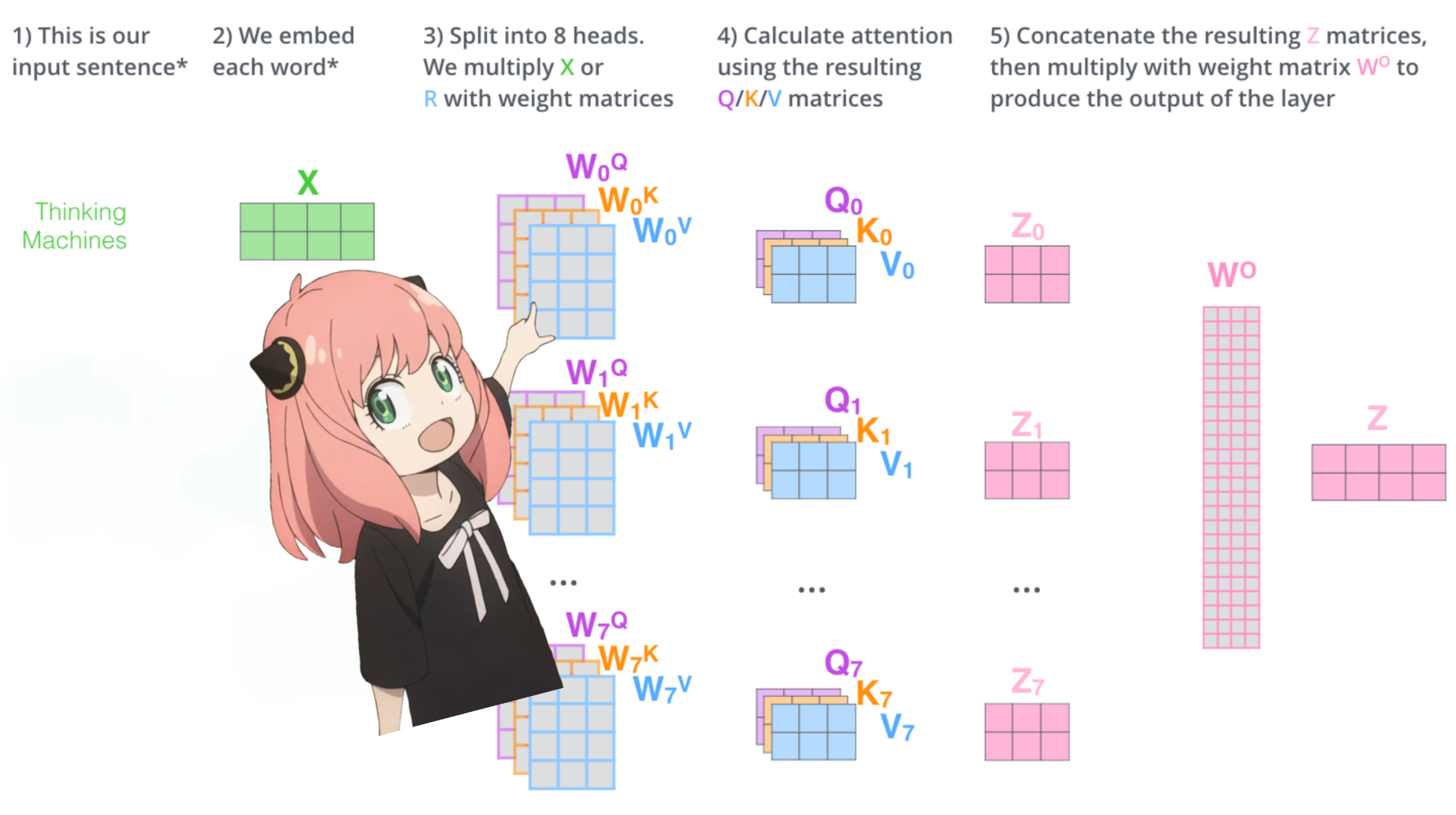
> モデルからクエリ、キー、値、出力ベクトルをロードすると、形状が [4096x4096]、[1024x4096]、[1024x4096]、[4096x4096] になることがわかります。
> 一見すると、これは奇妙です。なぜなら、理想的には、各頭に対して各 q、k、v、o が個別に必要だからです。
> コードの作成者は、アテンションヘッドの乗算を簡単に並列化できるため、これらをまとめてバンドルしました。
> 全てを開封してみます...
print (
model [ "layers.0.attention.wq.weight" ]. shape ,
model [ "layers.0.attention.wk.weight" ]. shape ,
model [ "layers.0.attention.wv.weight" ]. shape ,
model [ "layers.0.attention.wo.weight" ]. shape
) torch.Size([4096, 4096]) torch.Size([1024, 4096]) torch.Size([1024, 4096]) torch.Size([4096, 4096])
次のセクションでは、複数のアテンション ヘッドからのクエリをアンラップします。結果の形状は [32x128x4096] になります。
ここで、32 は llama3 のアテンション ヘッドの数、128 はクエリ ベクトルのサイズ、4096 はトークン埋め込みのサイズです。
q_layer0 = model [ "layers.0.attention.wq.weight" ]
head_dim = q_layer0 . shape [ 0 ] // n_heads
q_layer0 = q_layer0 . view ( n_heads , head_dim , dim )
q_layer0 . shape torch.Size([32, 128, 4096])
ここで、最初のレイヤーの最初のヘッドのクエリ重み行列にアクセスします。このクエリ重み行列のサイズは [128x4096] です。
q_layer0_head0 = q_layer0 [ 0 ]
q_layer0_head0 . shape torch.Size([128, 4096])
ここで、結果の形状が [17x128] であることがわかります。これは、17 個のトークンがあり、各トークンに対して 128 の長さのクエリがあるためです。

q_per_token = torch . matmul ( token_embeddings , q_layer0_head0 . T )
q_per_token . shape torch.Size([17, 128])
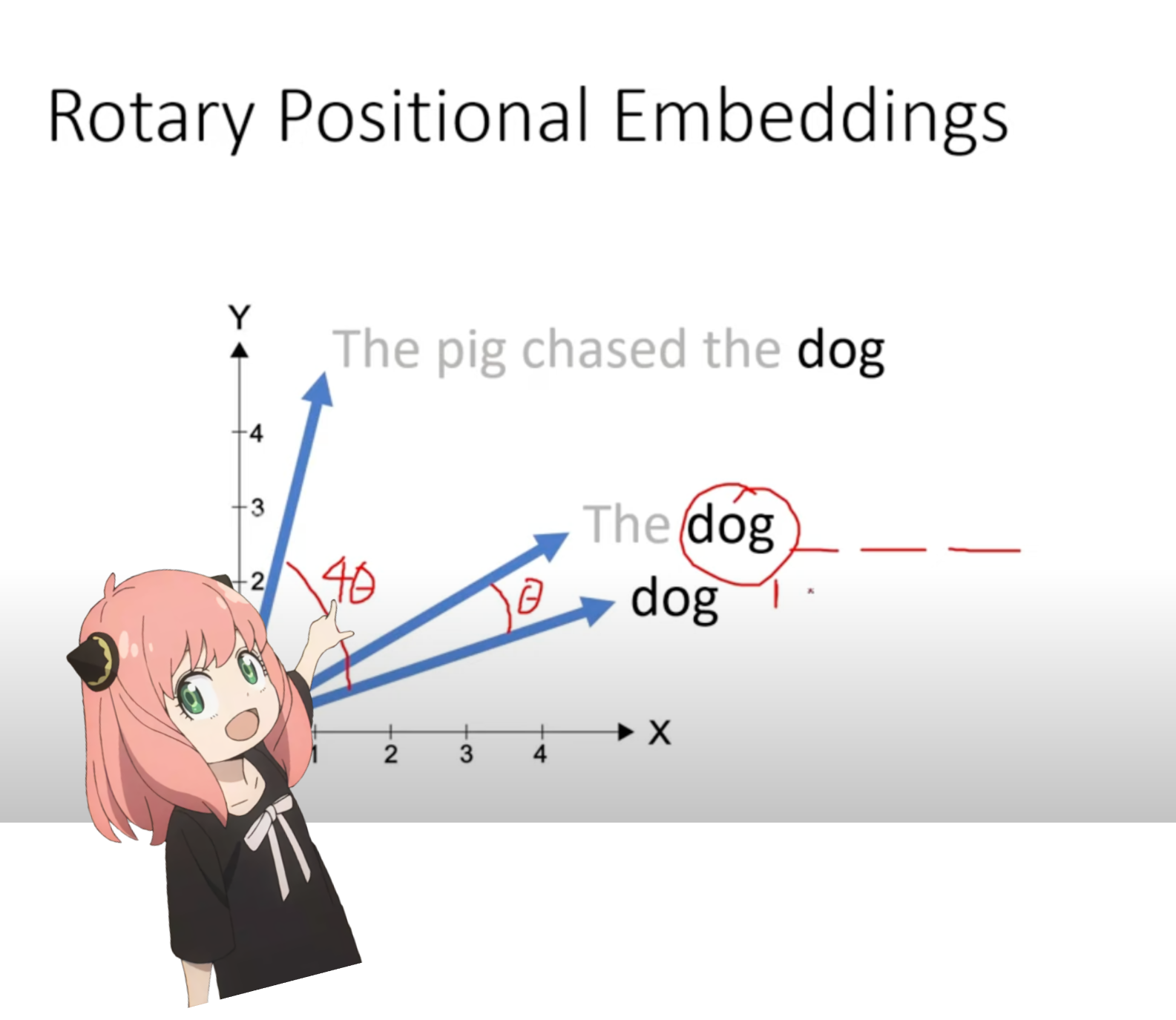
現在、プロンプト内の各トークンのクエリ ベクトルが用意されている段階にいます。しかしよく考えてみると、個々のクエリ ベクトルはプロンプト内の位置についてまったく知りません。
クエリ: 「生命、宇宙、そしてすべてについての究極の質問に対する答えは」
プロンプトでは「the」を 3 回使用しています。クエリ内の位置に基づいて、3 つすべての「the」トークンのクエリ ベクトルが異なるクエリ ベクトル (それぞれのサイズ [1x128]) を持つ必要があります。これらの回転は RoPE (回転位置埋め込み) を使用して実行します。
数学を理解するには、このビデオを見てください (これは私が見たものです)。 https://www.youtube.com/watch?v=o29P0Kpobz0&t=530s
q_per_token_split_into_pairs = q_per_token . float (). view ( q_per_token . shape [ 0 ], - 1 , 2 )
q_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
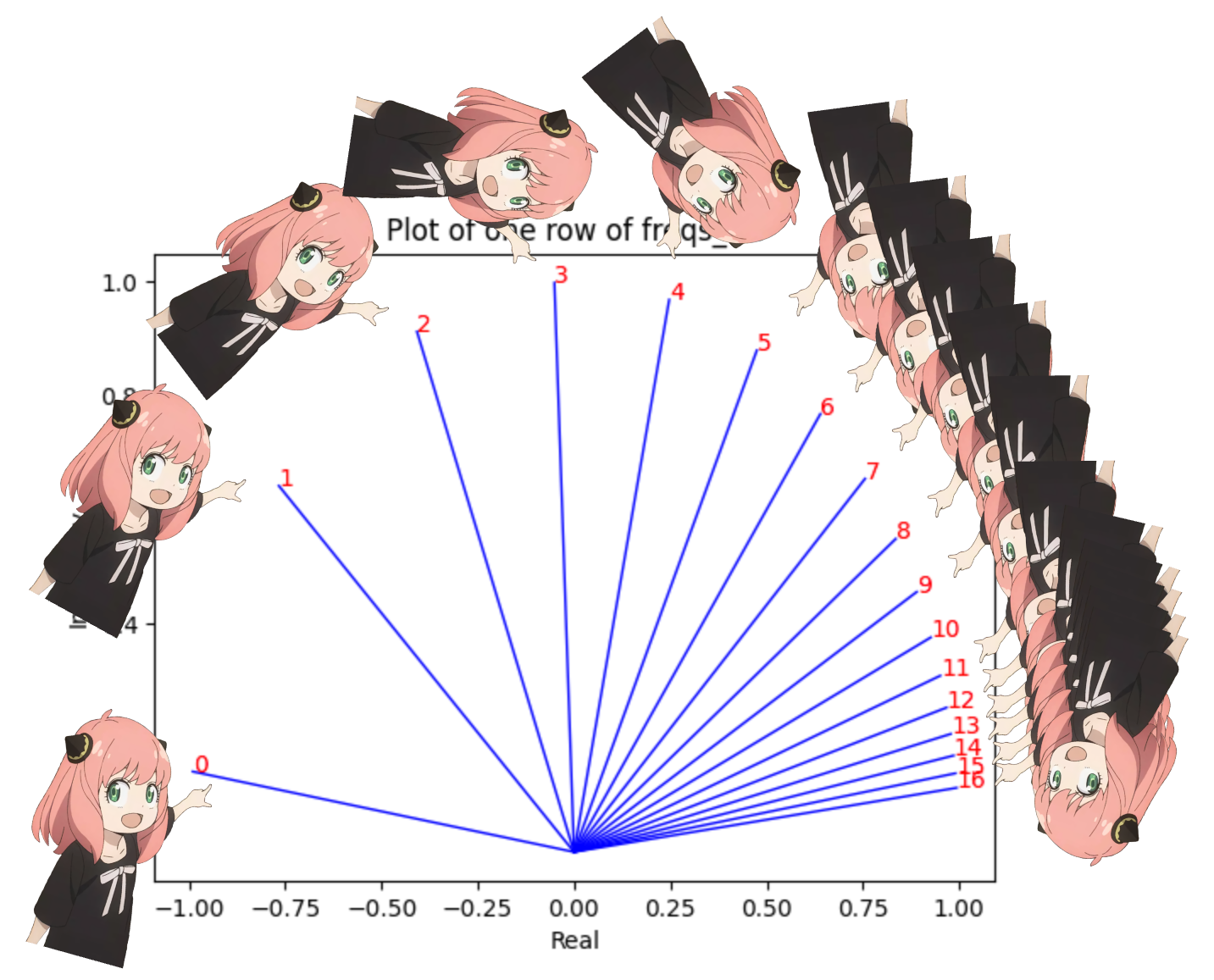
上記のステップでは、クエリ ベクトルをペアに分割し、各ペアに回転角度シフトを適用します。
サイズ [17x64x2] のベクトルができました。これは、プロンプト内のトークンごとに 64 のペアに分割された 128 個の長さのクエリです。これら 64 のペアはそれぞれ m*(シータ) だけ回転されます。ここで、m はクエリを回転するトークンの位置です。

zero_to_one_split_into_64_parts = torch . tensor ( range ( 64 )) / 64
zero_to_one_split_into_64_parts tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250,
0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656,
0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062,
0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469,
0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875,
0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281,
0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688,
0.9844])
freqs = 1.0 / ( rope_theta ** zero_to_one_split_into_64_parts )
freqs tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01,
2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01,
8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02,
2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03,
7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03,
2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04,
6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04,
1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05,
5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05,
1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06,
4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06])
freqs_for_each_token = torch . outer ( torch . arange ( 17 ), freqs )
freqs_cis = torch . polar ( torch . ones_like ( freqs_for_each_token ), freqs_for_each_token )
freqs_cis . shape
# viewing tjhe third row of freqs_cis
value = freqs_cis [ 3 ]
plt . figure ()
for i , element in enumerate ( value [: 17 ]):
plt . plot ([ 0 , element . real ], [ 0 , element . imag ], color = 'blue' , linewidth = 1 , label = f"Index: { i } " )
plt . annotate ( f" { i } " , xy = ( element . real , element . imag ), color = 'red' )
plt . xlabel ( 'Real' )
plt . ylabel ( 'Imaginary' )
plt . title ( 'Plot of one row of freqs_cis' )
plt . show ()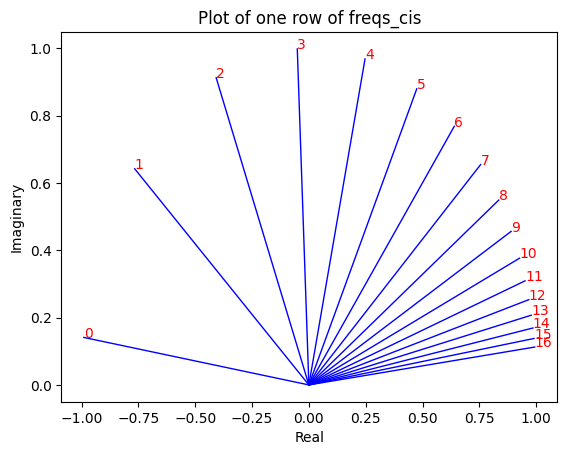
クエリ (ペアに分割したもの) を複素数として変換し、ドット積を使用して位置に基づいてクエリを回転できます。
正直に言って、これを考えるのは美しいことです:)
q_per_token_as_complex_numbers = torch . view_as_complex ( q_per_token_split_into_pairs )
q_per_token_as_complex_numbers . shape torch.Size([17, 64])
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cis
q_per_token_as_complex_numbers_rotated . shape torch.Size([17, 64])
複素数を再び実数として見ることで、クエリをペアとして返すことができます。
q_per_token_split_into_pairs_rotated = torch . view_as_real ( q_per_token_as_complex_numbers_rotated )
q_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
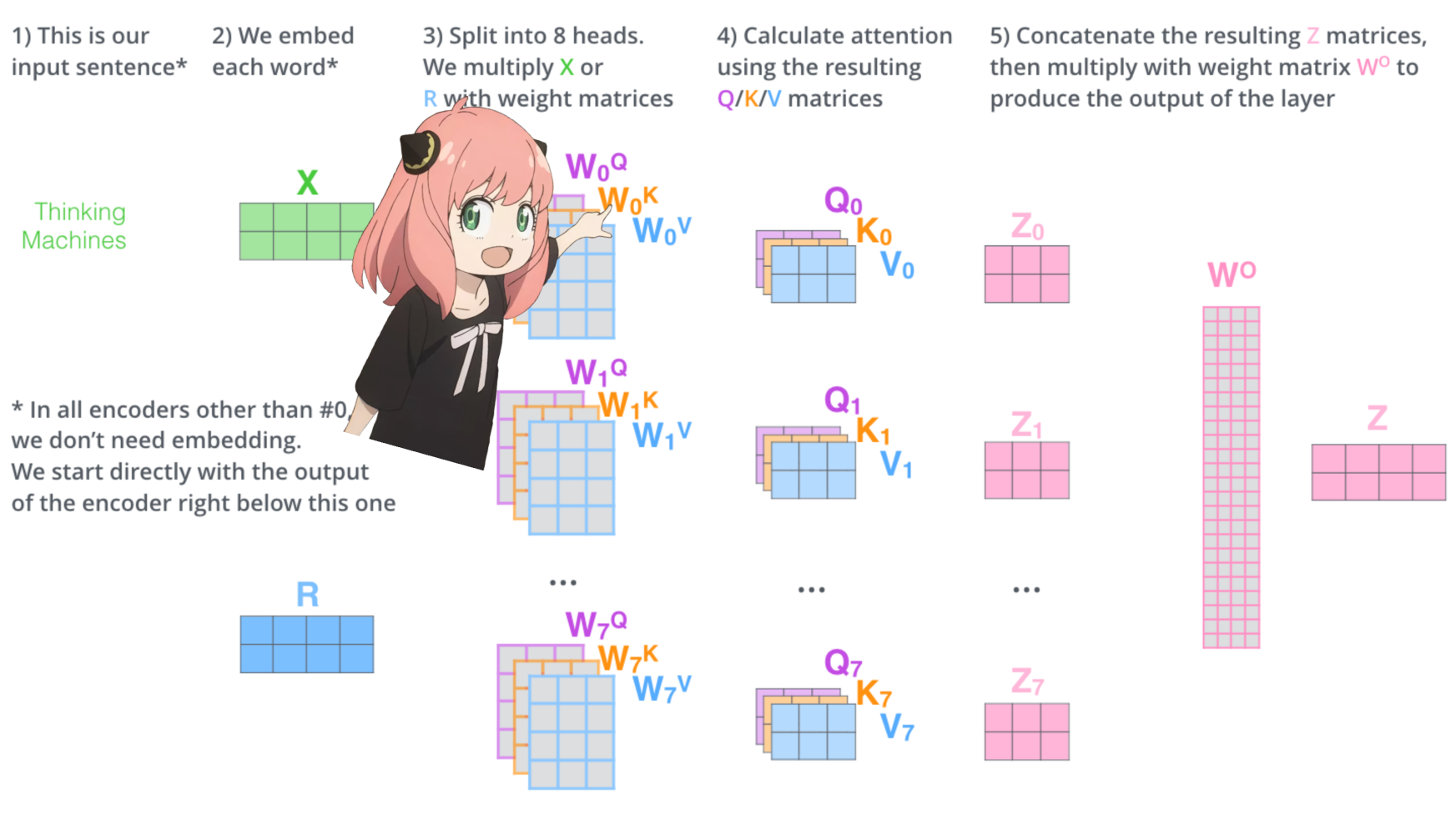
回転されたペアがマージされ、[17x128] の形状の新しいクエリ ベクトル (回転されたクエリ ベクトル) が得られます。ここで、17 はトークンの数、128 はクエリ ベクトルの次元です。
q_per_token_rotated = q_per_token_split_into_pairs_rotated . view ( q_per_token . shape )
q_per_token_rotated . shape torch.Size([17, 128])
k_layer0 = model [ "layers.0.attention.wk.weight" ]
k_layer0 = k_layer0 . view ( n_kv_heads , k_layer0 . shape [ 0 ] // n_kv_heads , dim )
k_layer0 . shape torch.Size([8, 128, 4096])
k_layer0_head0 = k_layer0 [ 0 ]
k_layer0_head0 . shape torch.Size([128, 4096])
k_per_token = torch . matmul ( token_embeddings , k_layer0_head0 . T )
k_per_token . shape torch.Size([17, 128])
k_per_token_split_into_pairs = k_per_token . float (). view ( k_per_token . shape [ 0 ], - 1 , 2 )
k_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
k_per_token_as_complex_numbers = torch . view_as_complex ( k_per_token_split_into_pairs )
k_per_token_as_complex_numbers . shape torch.Size([17, 64])
k_per_token_split_into_pairs_rotated = torch . view_as_real ( k_per_token_as_complex_numbers * freqs_cis )
k_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
k_per_token_rotated = k_per_token_split_into_pairs_rotated . view ( k_per_token . shape )
k_per_token_rotated . shape torch.Size([17, 128])
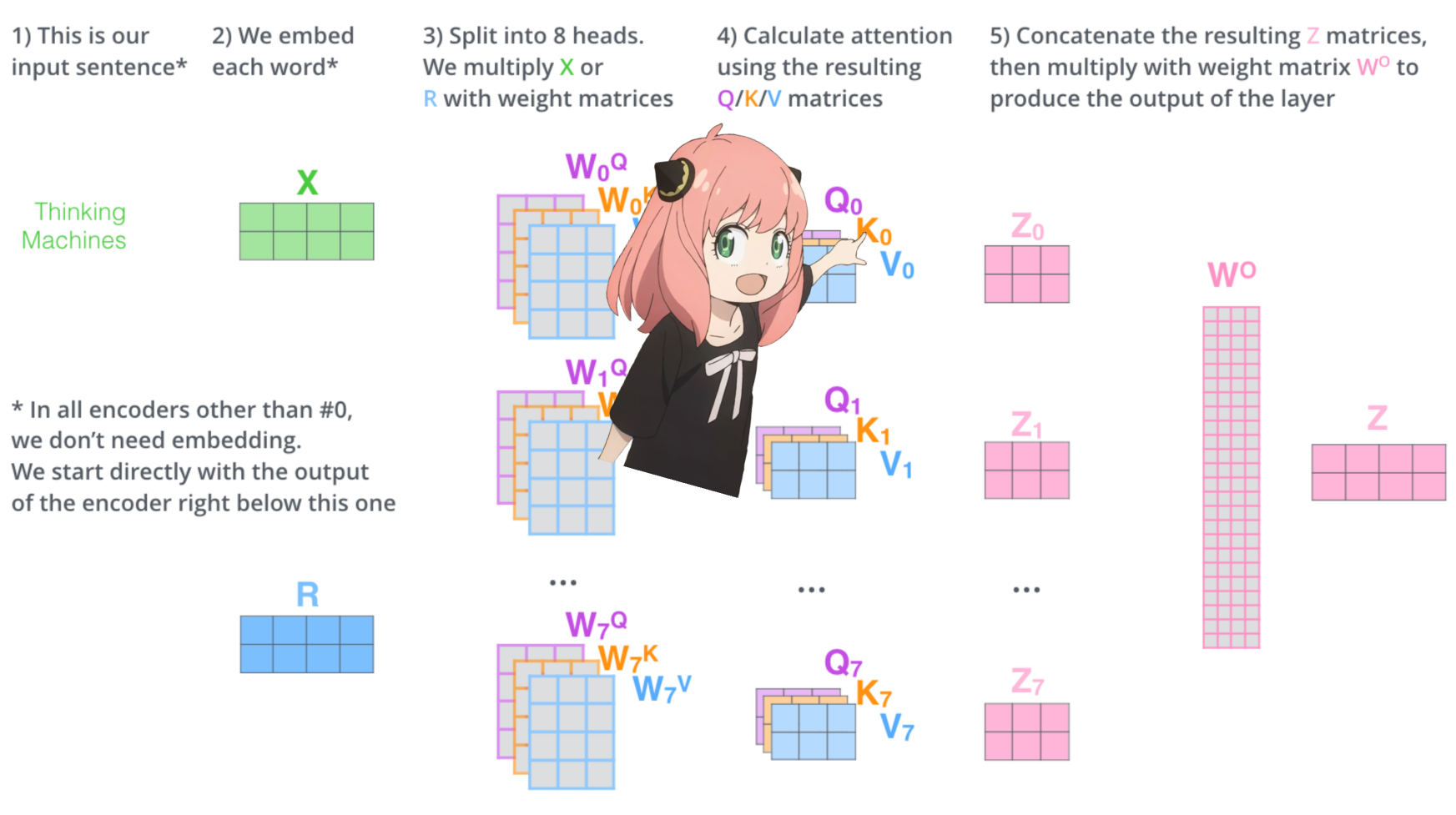
これにより、各トークンを相互にマッピングするスコアが得られます。
このスコアは、各トークンのクエリが各トークンのキーにどの程度関連しているかを示します。これはご注意ください:)
注意スコア行列 (qk_per_token) の形状は [17x17] です。ここで 17 はプロンプト内のトークンの数です
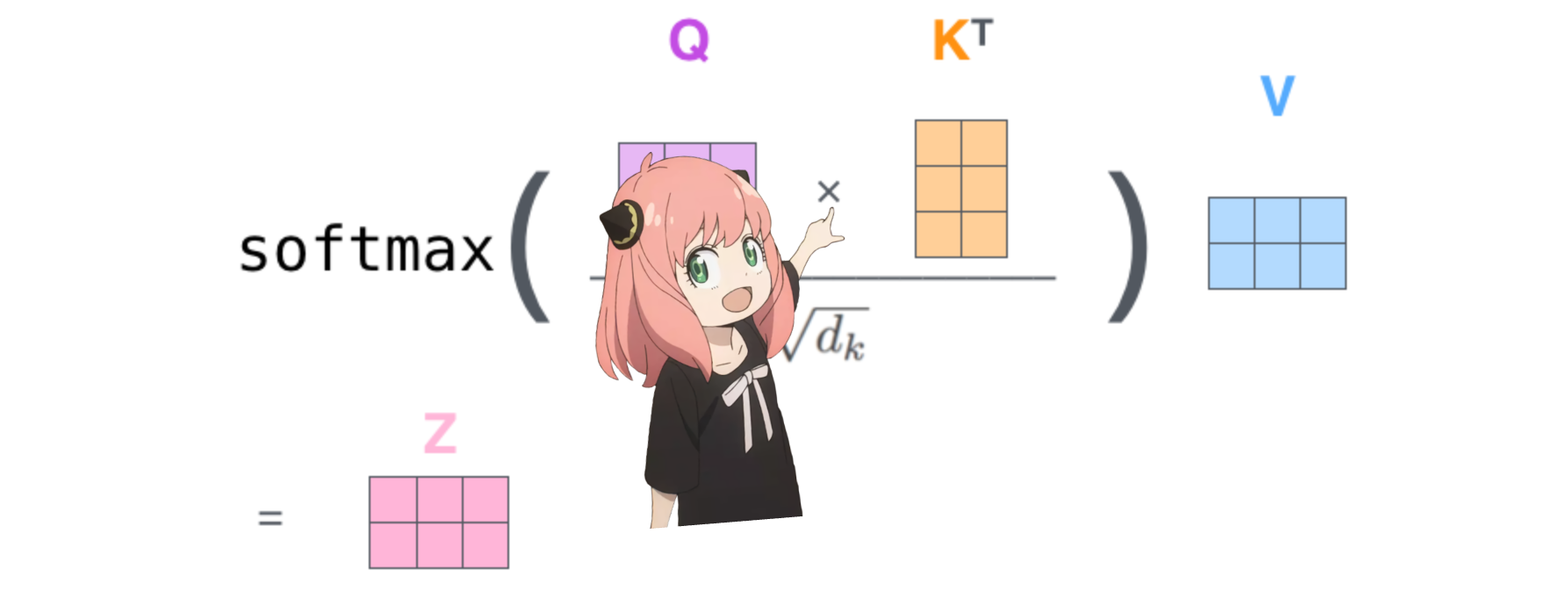
qk_per_token = torch . matmul ( q_per_token_rotated , k_per_token_rotated . T ) / ( head_dim ) ** 0.5
qk_per_token . shape torch.Size([17, 17])
llama3 のトレーニング プロセス中、将来のトークンの qk スコアはマスクされます。
なぜ?なぜなら、トレーニング中は過去のトークンを使用してトークンを予測することしか学習しないからです。
その結果、推論中に将来のトークンをゼロに設定します。
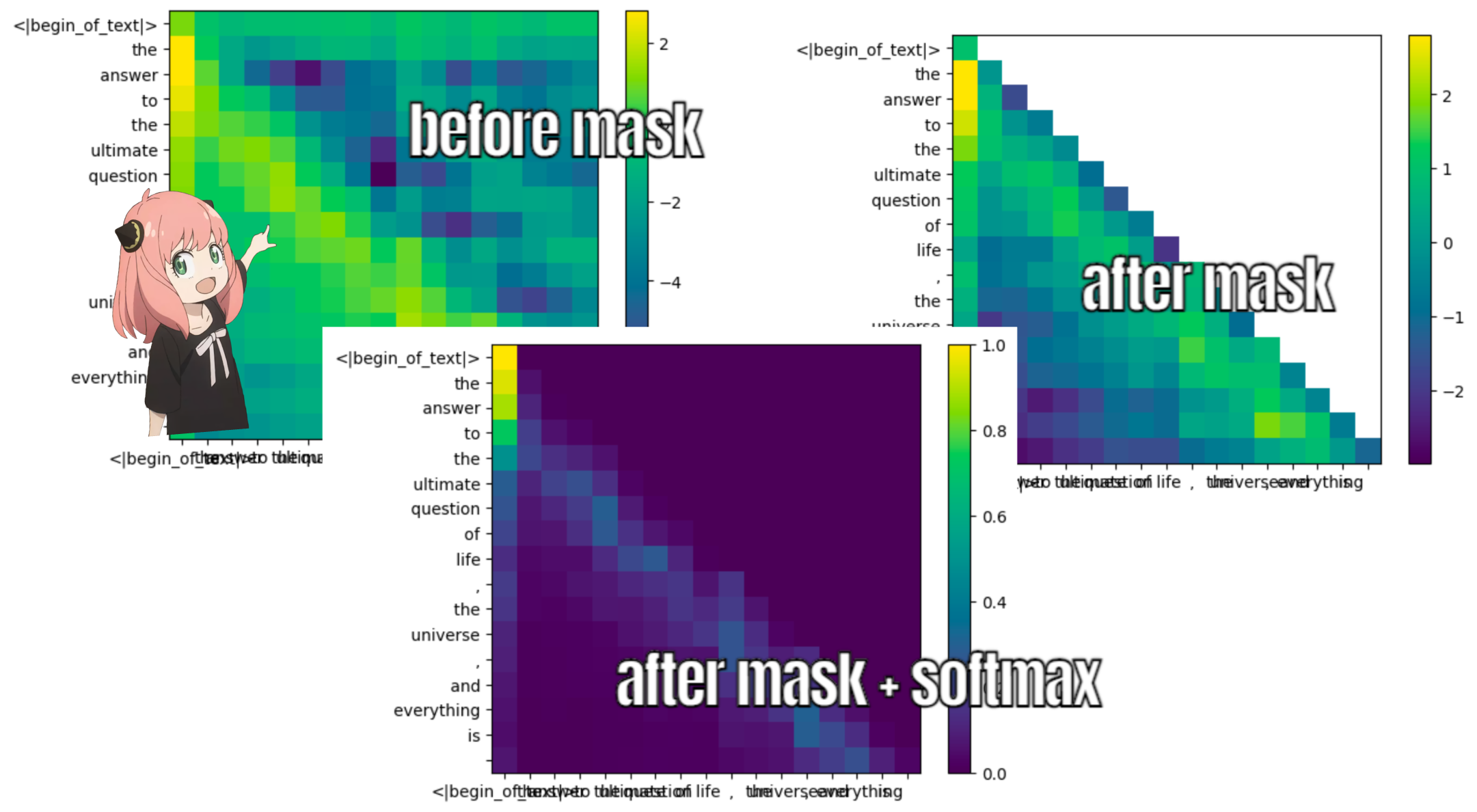
def display_qk_heatmap ( qk_per_token ):
_ , ax = plt . subplots ()
im = ax . imshow ( qk_per_token . to ( float ). detach (), cmap = 'viridis' )
ax . set_xticks ( range ( len ( prompt_split_as_tokens )))
ax . set_yticks ( range ( len ( prompt_split_as_tokens )))
ax . set_xticklabels ( prompt_split_as_tokens )
ax . set_yticklabels ( prompt_split_as_tokens )
ax . figure . colorbar ( im , ax = ax )
display_qk_heatmap ( qk_per_token )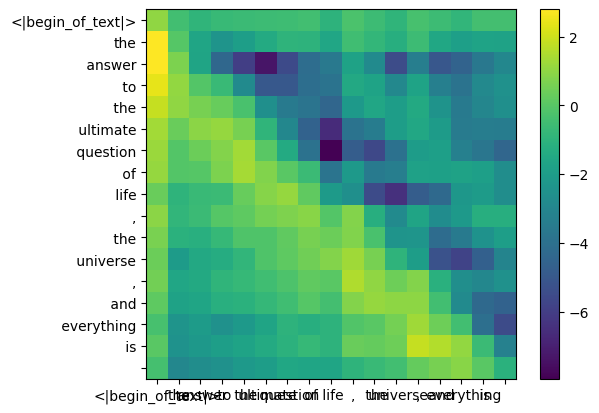
mask = torch . full (( len ( tokens ), len ( tokens )), float ( "-inf" ), device = tokens . device )
mask = torch . triu ( mask , diagonal = 1 )
mask tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
qk_per_token_after_masking = qk_per_token + mask
display_qk_heatmap ( qk_per_token_after_masking )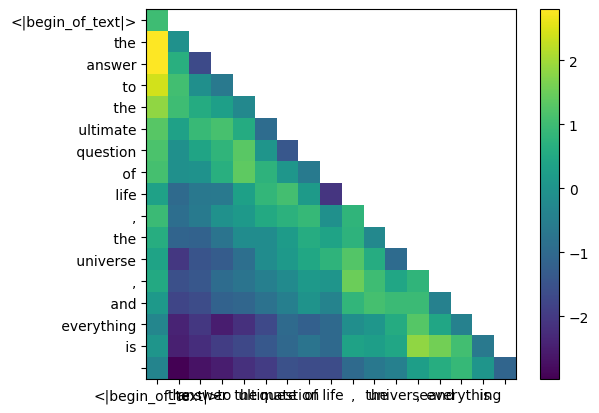
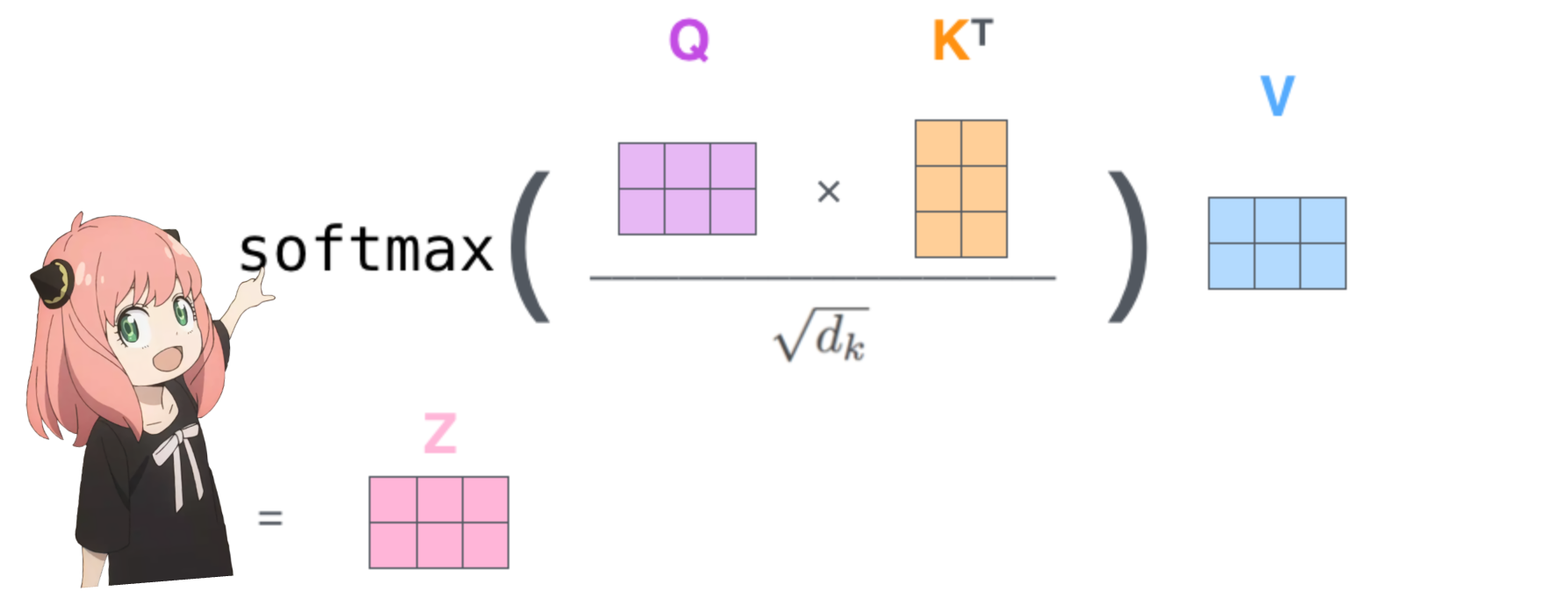
qk_per_token_after_masking_after_softmax = torch . nn . functional . softmax ( qk_per_token_after_masking , dim = 1 ). to ( torch . bfloat16 )
display_qk_heatmap ( qk_per_token_after_masking_after_softmax )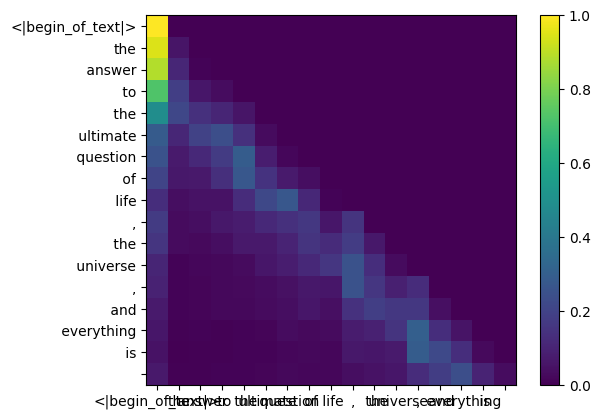
v_layer0 = model [ "layers.0.attention.wv.weight" ]
v_layer0 = v_layer0 . view ( n_kv_heads , v_layer0 . shape [ 0 ] // n_kv_heads , dim )
v_layer0 . shape torch.Size([8, 128, 4096])
最初の層、最初の頭部値の重み行列を以下に示します。
v_layer0_head0 = v_layer0 [ 0 ]
v_layer0_head0 . shape torch.Size([128, 4096])
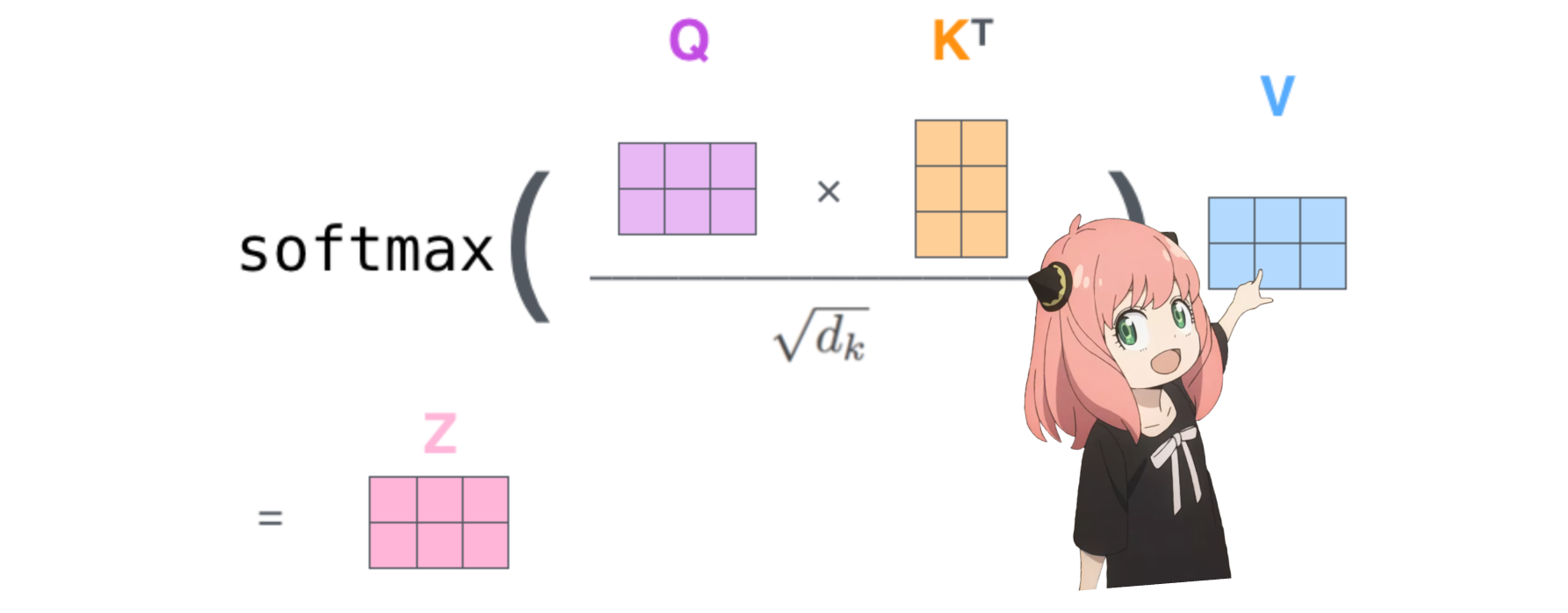
v_per_token = torch . matmul ( token_embeddings , v_layer0_head0 . T )
v_per_token . shape torch.Size([17, 128])
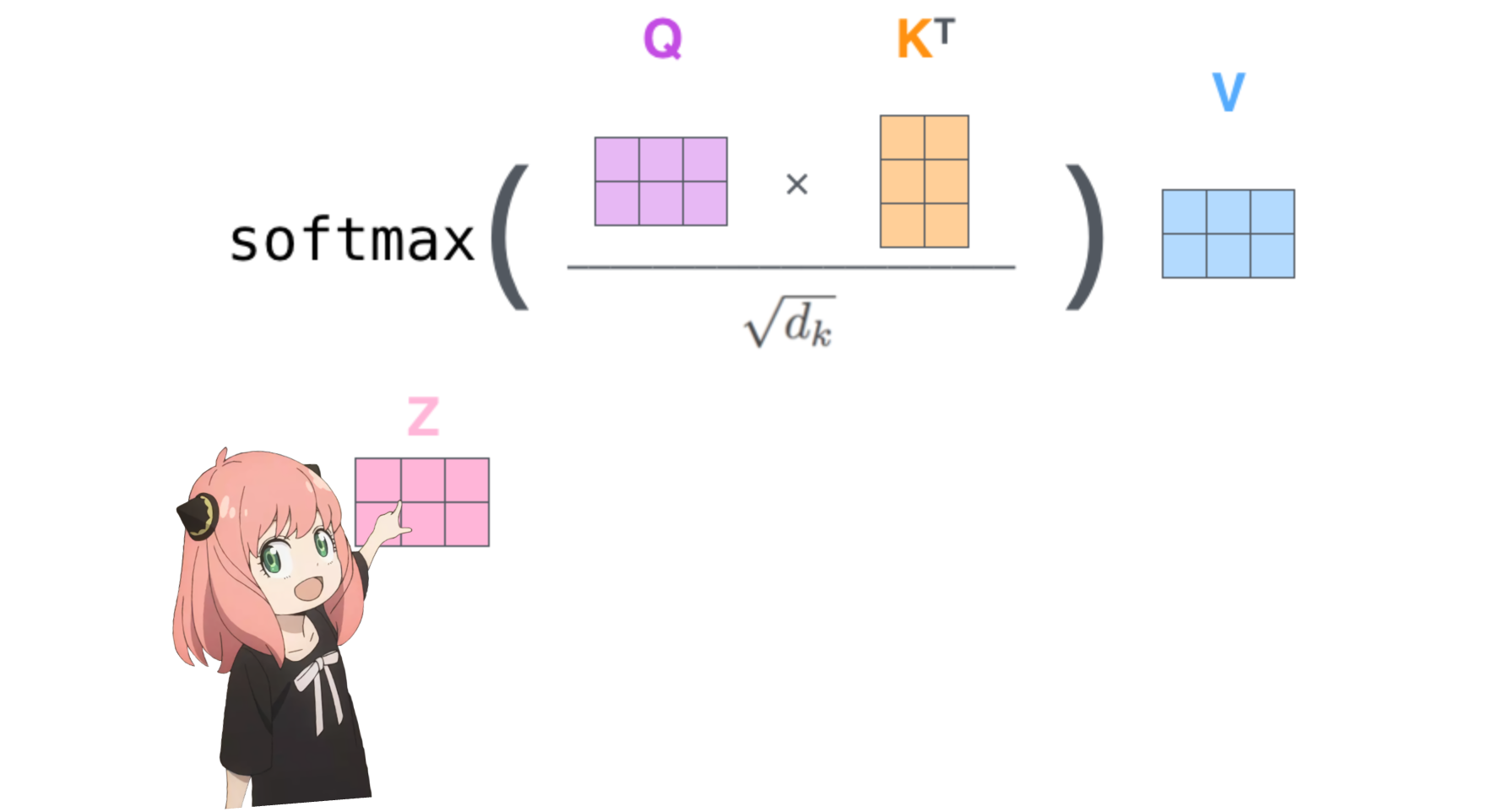
qkv_attention = torch . matmul ( qk_per_token_after_masking_after_softmax , v_per_token )
qkv_attention . shape torch.Size([17, 128])
