greta.gam: mgcv を使用した greta の一般化された加算モデル

greta.gam を使用すると、mgcv のスムーズな関数と数式構文を使用して、greta モデルで使用するスムーズな用語を定義できます。その後、モデルが完成する可能性を独自に定義し、MCMC によって適合させることができます。

これは進行中の作業です!

例

mgcv ?gamヘルプファイルを基にした簡単な例を次に示します。

mgcvの場合:

Gu & Wahba 4 term additive model # fit a model using gam() b <- gam(y ~ s(x2), data = dat)">

library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )

# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model

# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat )

同じモデルをgretaに当てはめます。

NULL # plot the data points(dat$x2, dat$y, pch = 19, cex = 0.2)">

library( greta.gam )
# > Loading required package: greta
# > 
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# > 
# >     binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# > 
# >     %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# >     eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# >     tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!               

# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )

# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))

# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )

# build model
m <- model( z_pred )

# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#>     warmup                                           0/1000 | eta:  ?s              warmup ==                                       50/1000 | eta: 30s              warmup ====                                    100/1000 | eta: 17s              warmup ======                                  150/1000 | eta: 12s              warmup ========                                200/1000 | eta: 10s              warmup ==========                              250/1000 | eta:  8s              warmup ===========                             300/1000 | eta:  7s              warmup =============                           350/1000 | eta:  6s              warmup ===============                         400/1000 | eta:  5s              warmup =================                       450/1000 | eta:  5s              warmup ===================                     500/1000 | eta:  4s              warmup =====================                   550/1000 | eta:  4s              warmup =======================                 600/1000 | eta:  3s              warmup =========================               650/1000 | eta:  3s              warmup ===========================             700/1000 | eta:  2s              warmup ============================            750/1000 | eta:  2s              warmup ==============================          800/1000 | eta:  1s              warmup ================================        850/1000 | eta:  1s              warmup ==================================      900/1000 | eta:  1s              warmup ====================================    950/1000 | eta:  0s              warmup ====================================== 1000/1000 | eta:  0s          
# >   sampling                                            0/200 | eta:  ?s            sampling ==========                                50/200 | eta:  1s            sampling ===================                      100/200 | eta:  0s            sampling ============================             150/200 | eta:  0s            sampling ======================================   200/200 | eta:  0s

# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])

# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL

# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )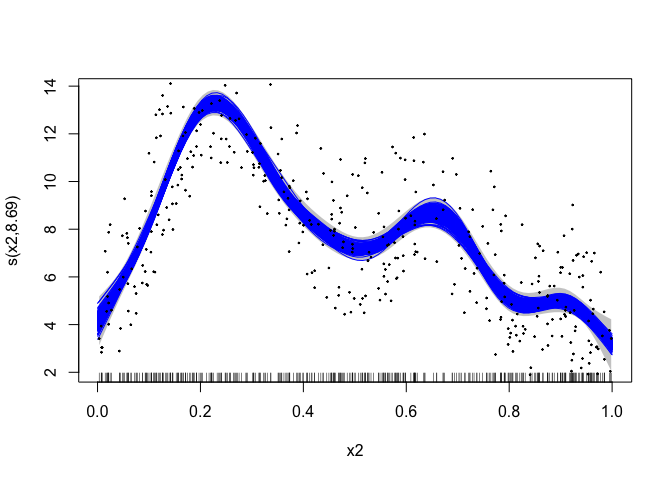

技術的な詳細の簡単な説明

greta.gam mgcvのjagam (Wood, 2016) ルーチンのいくつかのトリックを使用して、物事を機能させます。内部の仕組みに興味がある人向けに、簡単な詳細をいくつか紹介します。

GAM のベイズ解釈

GAM は、ベイズ解釈を備えたモデルです (「頻度主義」手法を使用して近似した場合でも)。よりスムーズなペナルティ行列は、ベイジアン変量効果モデルの事前精度行列と考えることができます。計画行列は、頻度主義の場合とまったく同じように構築されます。これに関する詳細な背景については、Miller (2021) を参照してください。

ペナルティ行列

GAM のベイジアン解釈には、単純な形式では事前分布がペナルティの零空間 (1D の場合、通常は線形項) として不適切であるという点で、若干の困難があります。適切な事前分布を取得するには、Marra & Wood (2011) で採用された「トリック」の 1 つを使用できます。それは、不適切な事前分布につながるペナルティの部分に何らかのペナルティを与えることです。私たちは、 jagamによって提供されるオプションを使用し、これらの項に対して追加のペナルティ行列を作成します (ペナルティ行列の固有分解から; Marra & Wood、2011 を参照)。