

PyPortfolioOpt は、古典的な平均分散最適化手法やブラック リッターマン割り当てなどのポートフォリオ最適化手法に加え、シュリンクや階層的リスク パリティなどのこの分野の最近の開発手法を実装するライブラリです。
これは広範でありながら簡単に拡張可能であり、カジュアルな投資家にも、簡単なプロトタイピング ツールを探している専門家にも役立ちます。あなたが少数の過小評価銘柄を特定したファンダメンタルズ志向の投資家であっても、さまざまな戦略を持つアルゴリズムトレーダーであっても、PyPortfolioOpt はリスク効率の高い方法でアルファソースを組み合わせるのに役立ちます。
PyPortfolioOpt が Journal of Open Source Software に掲載されました。
PyPortfolioOpt は現在 Tuan Tran によって保守されています。
ReadTheDocs のドキュメントにアクセスしてプロジェクトを詳しく調べるか、クックブックをチェックして、データのダウンロードからポートフォリオの構築までの完全なプロセスを示すいくつかの例を確認してください。
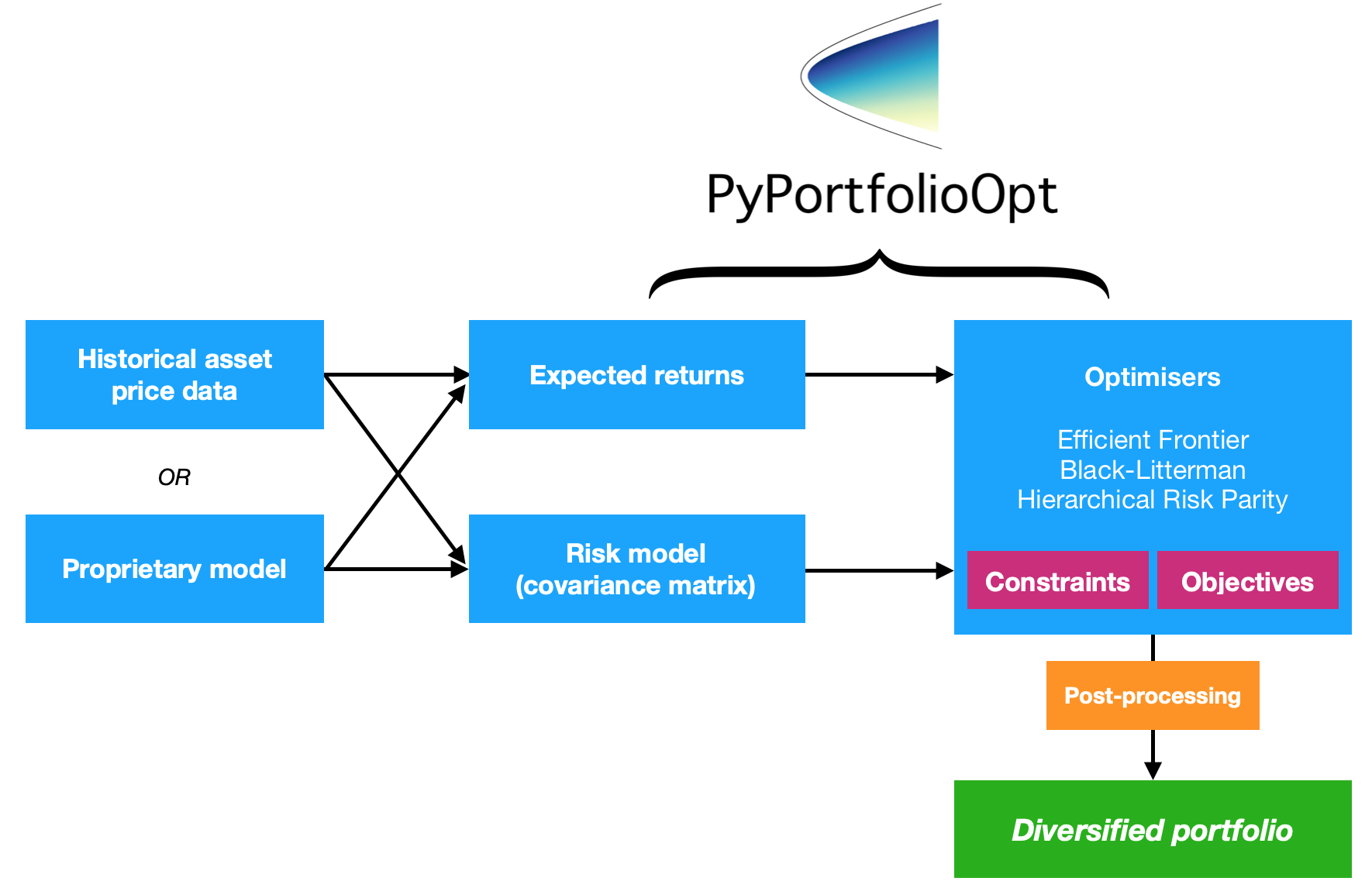
ブラウザで PyPortfolioOpt を対話的に操作したい場合は、ここで Binder を起動できます。セットアップには時間がかかりますが、すべての要件に対処することなくクックブックのレシピを試すことができます。
注: macOS ユーザーはコマンド ライン ツールをインストールする必要があります。
注: Windows を使用している場合は、まず C++ をインストールする必要があります。 (ダウンロード、インストール手順)
このプロジェクトは PyPI で利用できます。つまり、次のことが可能です。
pip install PyPortfolioOpt(cvxopt と cvxpy については、別のインストール手順に従う必要がある場合があります)。
ただし、仮想環境内で依存関係マネージャーを使用することがベスト プラクティスです。私の今のお勧めは、詩の準備を整えてから、ただ実行することです。
poetry add PyPortfolioOptそれ以外の場合は、プロジェクトをクローン/ダウンロードし、プロジェクト ディレクトリで次のコマンドを実行します。
python setup.py install PyPortfolioOpt は Docker をサポートします。 docker build -f docker/Dockerfile . -t pypfopt 。イメージを使用してテストを実行したり、Jupyter サーバーを起動したりすることもできます。
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bash詳細については、このガイドをお読みください。
これを独自のシステムと統合するために大幅な変更を加えたい場合は、このリポジトリのクローンを作成し、ソース コードのみを使用することがおそらく合理的です。
git clone https://github.com/robertmartin8/PyPortfolioOptあるいは、次のことを試してみることもできます。
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.git以下は実際の株式データの例で、シャープ レシオ (リスク調整後のリターンの尺度) を最大化するロングのみのポートフォリオを見つけるのがいかに簡単かを示しています。
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )これにより、次の重みが出力されます。
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28これは興味深いですが、それ自体では役に立ちません。ただし、PyPortfolioOpt は、上記の連続的な重みを実際に購入できる割り当てに変換できるメソッドを提供します。最新の価格と希望するポートフォリオ サイズ (この例では $10,000) を入力するだけです。
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89免責事項: このプロジェクトに関するいかなる内容も投資アドバイスを構成するものではなく、著者はその後の投資決定について一切の責任を負いません。詳細については、ライセンスを参照してください。
ハリー・マーコウィッツの 1952 年の論文は、ポートフォリオの最適化を芸術から科学に変えた紛れもない古典です。重要な洞察は、異なる期待リターンとボラティリティを持つ資産を組み合わせることで、目標リターンに対するリスクを最小限に抑える数学的に最適な配分を決定できるということです。そのようなすべての最適なポートフォリオのセットは、効率的フロンティアと呼ばれます。
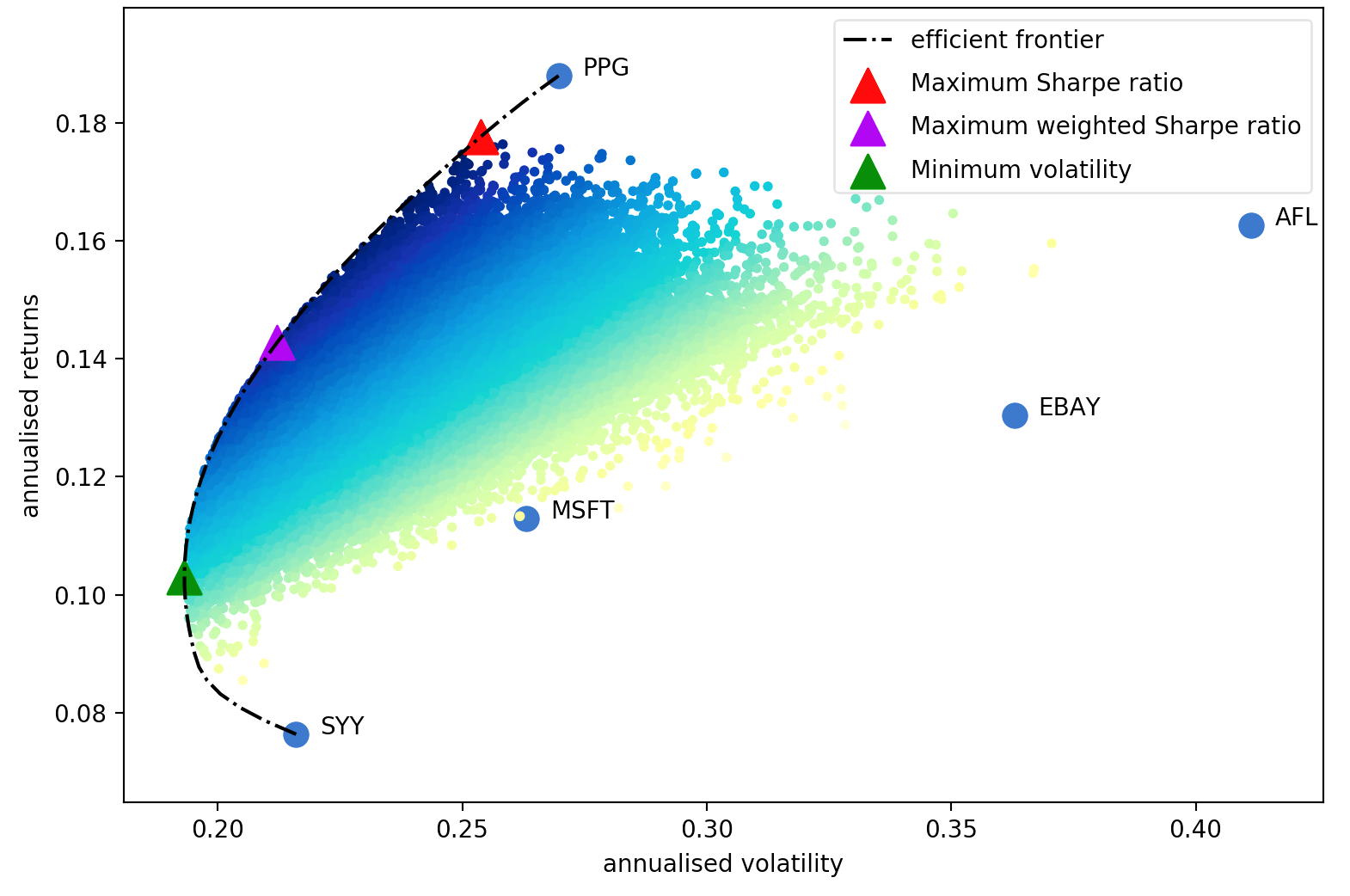
このテーマについては多くの発展が見られましたが、半世紀以上経った今でも、マーコウィッツの中核となる考え方は依然として基本的に重要であり、多くのポートフォリオ管理会社で日常的に使用されています。平均分散最適化の主な欠点は、理論的な処理には資産の期待収益と将来のリスク特性 (共分散) の知識が必要であることです。もちろん、株式生活の期待リターンがわかっていれば、はるかに簡単になるでしょうが、全体としては、株式のリターンを予測するのは悪名高いほど難しいということです。代わりに、過去のデータに基づいて期待リターンと共分散の推定値を導き出すことができます。ただし、マルコウィッツが提供する理論的な保証は失われますが、推定値が実際の値に近ければ近いほど、ポートフォリオはより良くなります。
したがって、このプロジェクトは 4 つの主要な機能セットを提供します (もちろん、それらは密接に関連しています)
PyPortfolioOpt の主な設計目標はモジュール性です。ユーザーは、PyPortfolioOpt が提供するフレームワークを利用しながら、コンポーネントを交換できる必要があります。
このセクションでは、PyPortfolioOpt で利用可能な機能の一部について詳しく説明します。他の例は、ここの Jupyter ノートブックで提供されています。もう 1 つの優れたリソースはテストです。
これのより包括的なバージョンは ReadTheDocs にあり、さらに上級ユーザー向けの拡張機能も提供されています。
共分散行列は、資産のボラティリティだけでなく、他の資産との相関関係もエンコードします。分散のメリットを享受するには(したがって単位リスク当たりの収益が増加するには)、ポートフォリオ内の資産は可能な限り相関関係を持たないようにする必要があるため、これは重要です。
sklearn.covarianceによって提供される効率的なベクトル化実装のラッパーを提供します。constant_variance 、 single_factor 、 constant_correlationという 3 つの収縮ターゲットを提供します。sklearn.covarianceに実装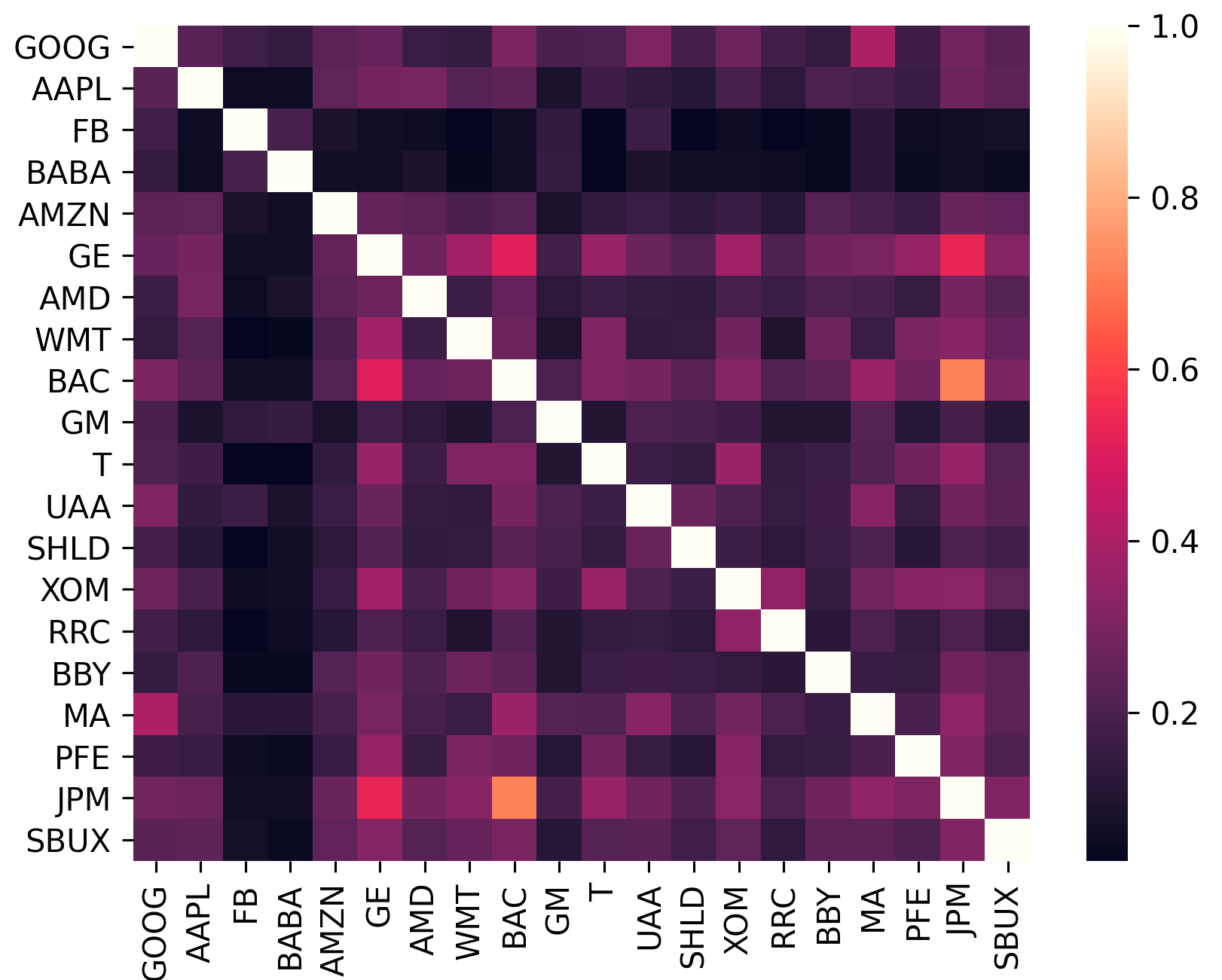
(このプロットは、 plotting.plot_covarianceを使用して生成されました)
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_riskメソッドとefficient_returnメソッドの場合、PyPortfolioOpt は、市場中立のポートフォリオ (つまり、重みの合計がゼロになる) を形成するオプションを提供します。これは、最大シャープ ポートフォリオと最小ボラティリティ ポートフォリオでは不可能です。これらの場合、レバレッジに関して不変ではないためです。市場の中立性には負の重みが必要です。 ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 ))平均分散の最適化に関する問題の 1 つは、重みがゼロになることが多くなるということです。これらはサンプル内では「最適」ですが、この特性により平均分散ポートフォリオがサンプル外でのパフォーマンスを下回る結果になることを示す多くの研究があります。そのために、目的関数のいずれかについて無視できる重みの数を減らすことができる目的関数を導入しました。基本的に、機械学習における L2 正則化によく似た項を使用して、小さな重みにペナルティ ( gammaでパラメータ化) を追加します。無視できない重みの望ましい数を達成するには、いくつかのgamma値を試すことが必要な場合があります。 20 銘柄のテスト ポートフォリオの場合、 gamma ~ 1十分です
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()v0.5.0 では、Black-Litterman 資産配分をサポートするようになりました。これにより、事前のリターン推定 (市場が示唆するリターンなど) と独自の見解を組み合わせて事後推定を作成できます。これにより、単に過去の平均リターンを使用するよりもはるかに優れた期待リターンの推定値が得られます。理論の説明や入力のフォーマットに関するアドバイスについては、ドキュメントを参照してください。
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe ()上記の機能は主に、二次計画法による平均分散最適化問題の解決に関連しています (ただし、これはcvxpyによって処理されます)。ただし、さまざまなオプティマイザーも提供しています。
詳細についてはドキュメントを参照してください。
テストは pytest で作成され (私の意見では、 unittestやその派生よりもはるかに直感的です)、100% に近いカバレッジを確保するように努めました。パッケージ ディレクトリに移動し、コマンド ラインでpytest実行するだけでテストを実行します。
PyPortfolioOpt は、20 ティッカーの日次収益のテスト データセットを提供します。
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]これらのティッカーは、いくつかの基準を満たすために非公式に選択されています。
現時点では、テストではすべてのエッジ ケースおよび目的関数とパラメーターの組み合わせが調査されていません。ただし、各メソッドとパラメータは意図したとおりに動作することがテストされています。
出版作品に PyPortfolioOpt を使用する場合は、JOSS 論文を引用してください。
引用文字列:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
ビブテックス::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}貢献は大歓迎です。詳細については、貢献ガイドをご覧ください。
2018 年のリリース以来、PyPortfolioOpt に貢献してくれたすべての人々に感謝したいと思います。特に次の方々に感謝の意を表します。