
これは、DSA.js ブックと NPM パッケージのリポジトリのコーディング実装です。
このリポジトリでは、JavaScript でのアルゴリズムとデータ構造の実装を見つけることができます。この資料は、開発者向けのリファレンス マニュアルとして使用したり、インタビューの前に特定のトピックを更新したりできます。また、問題をより効率的に解決するためのアイデアを見つけることもできます。
リポジトリのクローンを作成するか、NPM からコードをインストールできます。
npm install dsa.jsその後、それをプログラムまたは CLI にインポートできます。
const { LinkedList , Queue , Stack } = require ( 'dsa.js' ) ;利用可能なすべてのデータ構造とアルゴリズムのリストについては、index.js を参照してください。
アルゴリズムはすべてのプログラマーにとって不可欠なツールボックスです。
いくつか例を挙げると、データの並べ替え、大きなデータセット内の値の検索、データの変換、多くのユーザーに合わせてコードを拡張する必要がある場合には、アルゴリズムの実行時間を考慮する必要があります。アルゴリズムは問題を解決するために従うステップにすぎませんが、データ構造は後で操作するためにデータを保存する場所です。両方を組み合わせてプログラムを作成します。
アルゴリズム + データ構造 = プログラム。
実際、ほとんどのプログラミング言語とライブラリは、基本的なデータ構造とアルゴリズムの実装を提供します。ただし、データ構造を適切に利用するには、ジョブに最適なツールを選択するためのトレードオフを理解する必要があります。
この教材では次のことを学びます。
すべてのコードと説明はこのリポジトリで入手できます。 (src フォルダー) からリンクとコード例を調べることができます。ただし、インライン コードのサンプルは展開されません (Github の asciidoc 制限のため)。ただし、パスに従って実装を確認できます。
注: 情報をより直線的に利用したい場合は、書籍形式の方が適しています。
以下に示すように、トピックは 4 つの主要なカテゴリに分類されます。
複雑な問題を一切省いたコンピューター サイエンスの要点。 (クリックすると拡大します)
面倒なことを一切省いたコンピューター サイエンスの要点
コード例から実行時間の計算方法を学ぶ
Big O 表記法を使用してアルゴリズムを比較する方法を学びます。 (クリックすると拡大します)
Big O 表記法を使用してアルゴリズムを比較する方法を学びます。
Big O 記法を使用したアルゴリズムの比較
配列上の重複を見つけたいとします。 Big O 表記を使用すると、同じ問題を解決しても、解決にかかる時間に大きな違いがあるさまざまなソリューションを比較できます。
- マップを活用した最適解
- 配列内の重複の検索 (素朴なアプローチ)
時間計算量の計算方法をコードで説明する 8 つの例。 (クリックすると拡大します)
時間計算量の計算方法をコードで説明する 8 つの例
最も一般的な時間計算量
時間計算量グラフ
最も一般的なデータ構造の詳細を理解します。 (クリックすると拡大します)
最も一般的なデータ構造の詳細を理解する
配列: ほとんどの言語に組み込まれているため、ここでは実装されていません。配列の時間計算量
リンク リスト: 各データ ノードには次 (および前) へのリンクがあります。コード |リンクリストの時間計算量
キュー: データは「先入れ先出し」(FIFO) 方式で流れます。コード |キュー時間の複雑さ
スタック: データは「後入れ先出し」(LIFO) 方式で流れます。コード |スタック時間の複雑さ
配列またはリンク リストを使用する場合。トレードオフを理解してください。 (クリックすると拡大します)
配列またはリンク リストを使用する場合。トレードオフを知る
配列を使用する場合…
- (インデックスを使用して) ランダムな順序でデータに高速にアクセスする必要があります。
- データは多次元です (行列、テンソルなど)。
次の場合にリンク リストを使用します。
- データに順次アクセスします。
- メモリを節約し、必要な場合にのみメモリを割り当てたいと考えています。
- リストの両端から削除/追加するには一定の時間が必要です。
- サイズ要件が不明な場合 - 動的なサイズの利点
リスト、スタック、キューを構築します。 (クリックすると拡大します)
リスト、スタック、キューを最初から構築する
これらのデータ構造のいずれかを最初から構築します。
- リンクされたリスト
- スタック
- 列
すべてのデータ構造の中で最も汎用性の高いデータ構造の 1 つであるハッシュ マップについて理解します。 (クリックすると拡大します)
ハッシュマップ
次のようなさまざまなタイプのマップを実装する方法を学びます。
- ハッシュマップ
- ツリーマップ
また、さまざまな Maps 実装の違いについても学習してください。
HashMap時間効率がより優れています。TreeMapスペース効率がより優れています。TreeMap検索複雑さはO(log n)ですが、最適化されたHashMapは平均O(1)です。HashMapのキーは挿入順です (実装によってはランダムです)。TreeMapのキーは常にソートされます。TreeMap、最小値の取得、最大値の取得、中央値の取得、キーの範囲の検索などのいくつかの統計データを無料で提供します。HashMapそうではありません。TreeMap常にO(log n)が保証されていますが、HashMapの償却時間はO(1)ですが、再ハッシュのまれなケースではO(n)がかかります。グラフとツリーのプロパティを理解します。 (クリックすると拡大します)
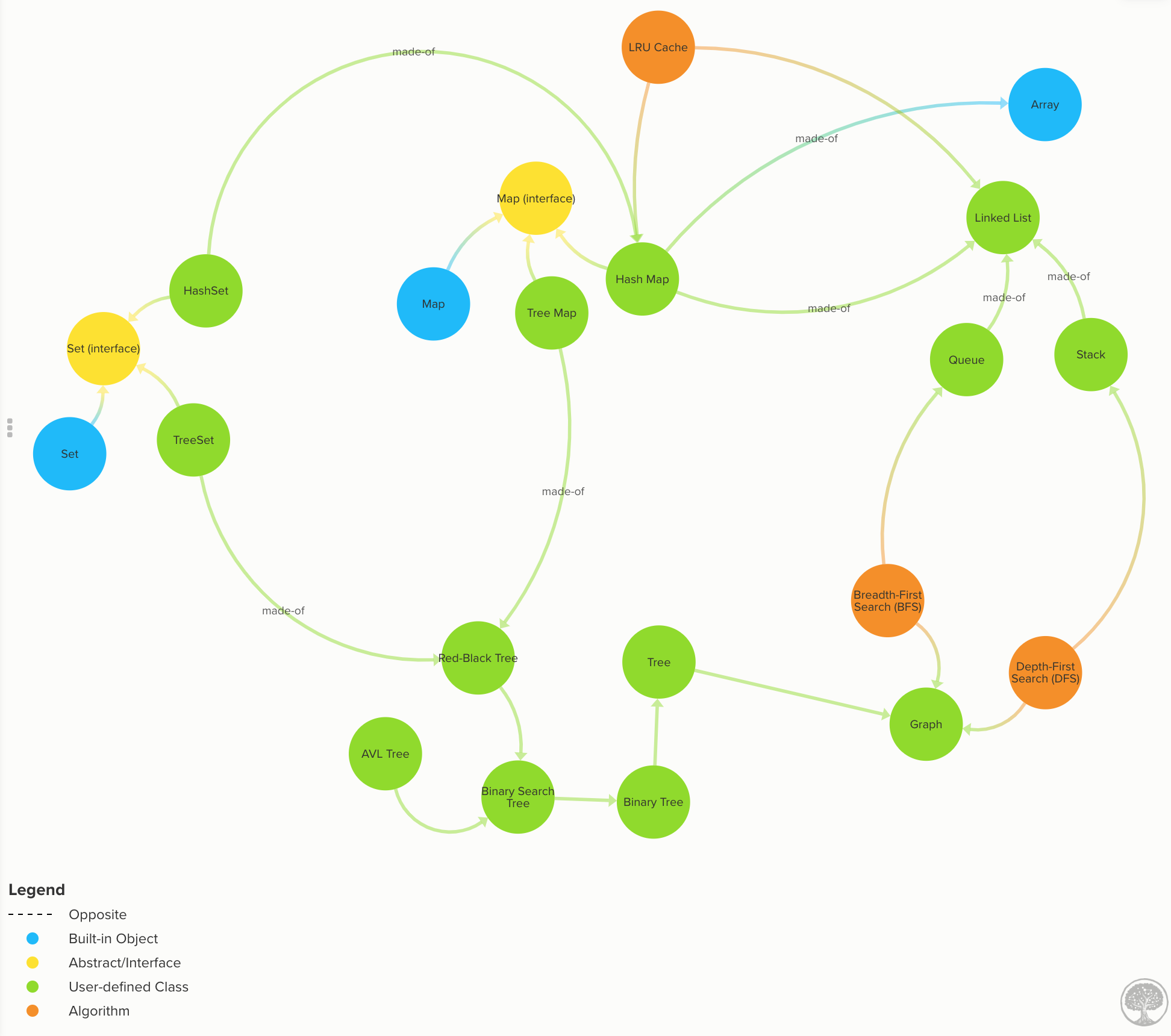
グラフとツリーの性質を知る
グラフ
豊富な画像とイラストでグラフのプロパティをすべて把握できます。
グラフ: 0 個以上の隣接ノードへの接続またはエッジを持つことができるデータノード。ツリーとは異なり、ノードは複数の親ループを持つことができます。コード |グラフの時間計算量
木々
さまざまな種類の木とその性質について学びましょう。
ツリー: データ ノードには 0 個以上の隣接ノード (子) があります。各ノードは親ノードを 1 つだけ持つことができ、それ以外の場合はツリーではなくグラフになります。コード |ドキュメント
Binary Trees : ツリーと同じですが、子は最大 2 つしか持つことができません。コード |ドキュメント
二分探索ツリー(BST): 二分木と同じですが、ノード値は
left < parent < right順序を保ちます。コード | BST 時間計算量AVL ツリー: ルックアップ時間を最大化する自己バランス型 BST。コード | AVL ツリーのドキュメント |セルフバランスとツリーの回転に関するドキュメント
赤黒ツリー: 挿入速度を最大化するために、AVL よりも緩めのセルフバランス BST。コード
高速検索のために二分探索ツリーを実装します。
高速検索のための二分探索ツリーを実装する
ツリー内の値を追加/削除/更新する方法を学習します。
バランスのとれた木を作るにはどうすればよいでしょうか?
アンバランスBSTからバランスBSTへ
1 2 / 2 => 1 3 3
7 つの簡単なステップで問題解決に行き詰まる必要はありません。 (クリックすると拡大します)
8 つの簡単なステップで問題解決に行き詰まることはありません
- 問題を理解する
- 簡単な例を構築します (エッジケースはまだありません)
- ソリューションのブレインストーミング (貪欲なアルゴリズム、分割統治、バックトラッキング、ブルート フォース)
- 簡単な例で答えをテストしてください (精神的に)
- ソリューションを最適化する
- コードを書きます。はい、コーディングできるようになりました。
- 書いたコードをテストする
- 空間と時間の両方の複雑さを分析し、さらに最適化します。
詳細はこちら
最も一般的な並べ替えアルゴリズム (マージ ソート、クイックソートなど) をマスターします(クリックして展開)
最も一般的な並べ替えアルゴリズムをマスターする
オーバーヘッドが低い 3 つの重要な並べ替えアルゴリズム O(n^2) を検討します。
バブルソート。コード |ドキュメント
挿入ソート。コード |ドキュメント
選択の並べ替え。コード |ドキュメント
次に、次のような効率的な並べ替えアルゴリズム O(n log n) について説明します。
マージソート。コード |ドキュメント
クイックソート。コード |ドキュメント
分割統治、動的プログラミング、貪欲アルゴリズム、バックトラッキングなど、問題を解決するためのさまざまなアプローチを学びます。 (クリックすると拡大します)
アルゴリズムの問題を解決するためのさまざまなアプローチを学ぶ
アルゴリズムの問題を解決するための次のテクニックについて説明します。
- 貪欲なアルゴリズム: ヒューリスティックを使用して貪欲な選択を行い、過去を振り返ることなく最適なソリューションを見つけます。
- 動的プログラミング:重複する部分問題が多数ある場合に、再帰的アルゴリズムを高速化する手法。作業の重複を避けるためにメモ化を使用します。
- 分割して征服: 問題を小さな部分に分割し、それぞれの下位問題を克服してから、結果を結合します。
- バックトラッキング: 考えられるすべて (または一部) のパスを検索します。ただし、現在のソリューションが機能していないことに気付くとすぐに停止し、元に戻ります。
- ブルート フォース: 考えられるすべての解決策を生成し、すべてを試行します。 (最後の手段として、または出発点として使用してください)。
プログラマーとして、私たちは毎日問題を解決しなければなりません。問題をうまく解決したい場合は、幅広い解決策について知っておくと良いでしょう。多くの場合、自分で答えを見つけるよりも、既存のリソースを学ぶ方が効率的です。ツールと練習が多ければ多いほど、より良い結果が得られます。この本は、データ構造間のトレードオフを理解し、アルゴリズムのパフォーマンスについて推論するのに役立ちます。
JavaScript のアルゴリズムに関する書籍はあまりありません。この材料は隙間を埋めます。また、それは良い練習です:)
はい、[slack チャネル](https://dsajs-slackin.herokuapp.com) で問題を開いたり、質問したりできます。
このプロジェクトは書籍としても出版されています。 180 ページ以上、ePub および Mobi バージョンを含む、適切にフォーマットされた PDF が得られます。
以下のいずれかの場所までご連絡ください。
@iAmAdrianMejiadsajs.slack.comでチャットする