ホーム|インストール|ドキュメント|チュートリアル|開発者
robeo は、確率数値を使用して常微分方程式 (ODE) を解く高速 Python ライブラリです。つまり、ほとんどの ODE ソルバー (オイラー法など) は、ステップ サイズのグリッド上で ODE への決定論的近似を生成します。
Rodeo は、多くの確率ソルバーに共通する非線形ベイジアン フィルター パラダイムへの軽量で拡張可能な近似ファミリーを提供します (Tronarp et al (2018))。これは、ODE 解の前にガウス プロセスを配置し、ソルバーがグリッドを通過するにつれて逐次的に更新することから始まります。 robeoはjax上に構築されており、ジャストインタイムのコンパイルと自動微分が可能です。 jaxの API はnumpyの API とほぼ同等です。
robeo は2 つの主要なツールを提供します。1 つは ODE 解の近似用で、もう 1 つはパラメーター推論用です。前者については、以下を提供します。
solve : 非線形ベイジアン フィルタリング パラダイムを使用する確率的 ODE ソルバーの実装。後者については、尤度近似法を提供します。
basic : 基本的な尤度近似法の実装 (詳細は Wu and Lysy (2023) を参照)。fenrir : フェンリルの実装 (Tronarp et al (2022))。marginal_mcmc : Chkrebtii のメソッドの MCMC 実装 (Chkrebtii et al (2016))。dalton : データ適応 ODE 尤度近似の実装 (Wu および Lysy (2023))。詳しい使用例は「ドキュメント」セクションにあります。これは、 rodeoのjaxのみのバージョンであることに注意してください。他のさまざまなバックエンドを使用するレガシー バージョンについては、ここを参照してください。
GitHub からリポジトリをダウンロードし、 setup.cfgスクリプトを使用してインストールします。
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . まず readthedocs にアクセスして、次の例のレンダリングされたドキュメントを参照してください。
簡単な ODE 問題を解決するためのクイックスタート チュートリアル。
高次常微分方程式を解く例。
難しいカオス ODE を解く例。
ラプラス近似を使用するパラメータ推論問題の例。
このウォークスルーでは、確率ソルバーを使用して ODE を解く方法と、パラメーター推論を実行する方法の両方を示します。まず、ODE を解くためのセットアップを説明します。そのために、次の最初に順序付けされた ODE の例 ( FitzHugh-Nagumoモデル) を考えてみましょう。
解決策はどこにあるのか
(Wu and Lysy (2023)) の表記に従って、次のようになります。
のために
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
)ソルバーからの解を、 scipyライブラリのodeintによって提供される決定論的解と比較します。
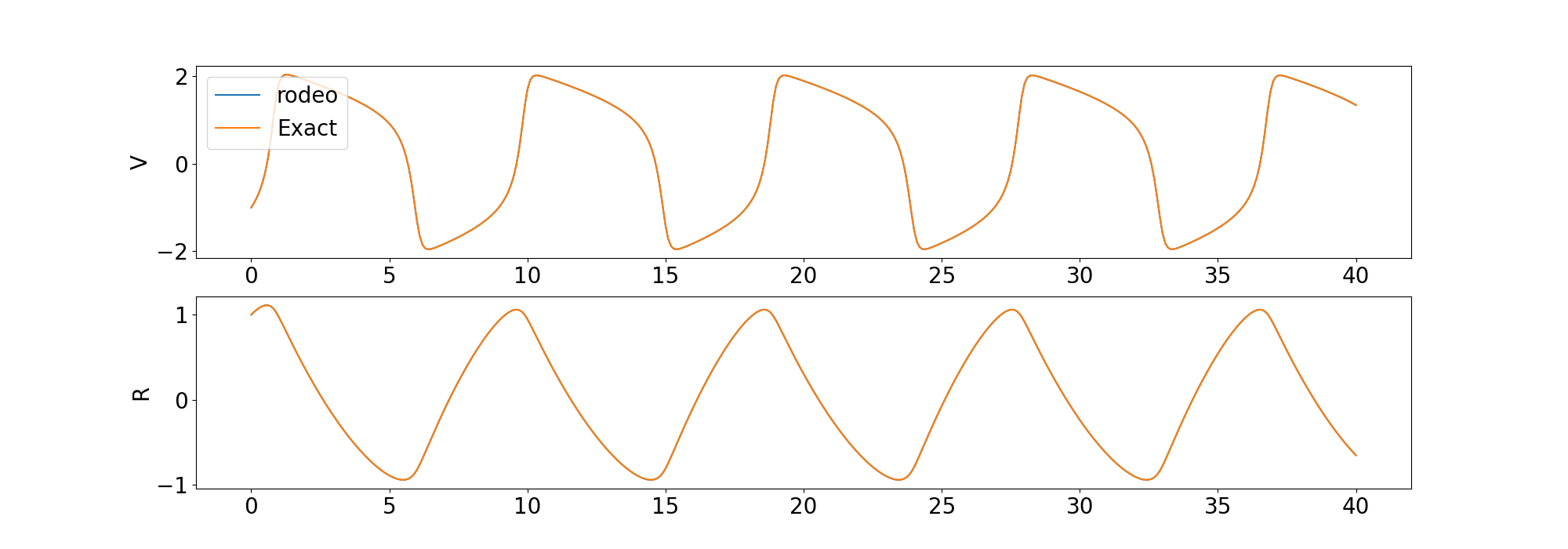
高次常微分方程式とカオス常微分方程式を解く例も含まれています。
次に、パラメータ推論の問題に移ります。 robeo には、 「説明」セクションにまとめられたいくつかの尤度近似法が含まれています。ここでは、 basic尤度近似法を使用します。観測がモデルを介してシミュレートされたと仮定します。
どこbasic尤度近似を構築できます。
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars ))これは使用法を示す基本的な例です。解の不確実性をfenrir 、 marginal_mcmc 、 daltonなどの尤度近似に伝播する、より洗練された尤度近似を提案します。詳細については、パラメーター推論のチュートリアルを参照してください。
/examples/のRodeoで見つかったさまざまな尤度近似によって生成された結果の一部を次に示します。
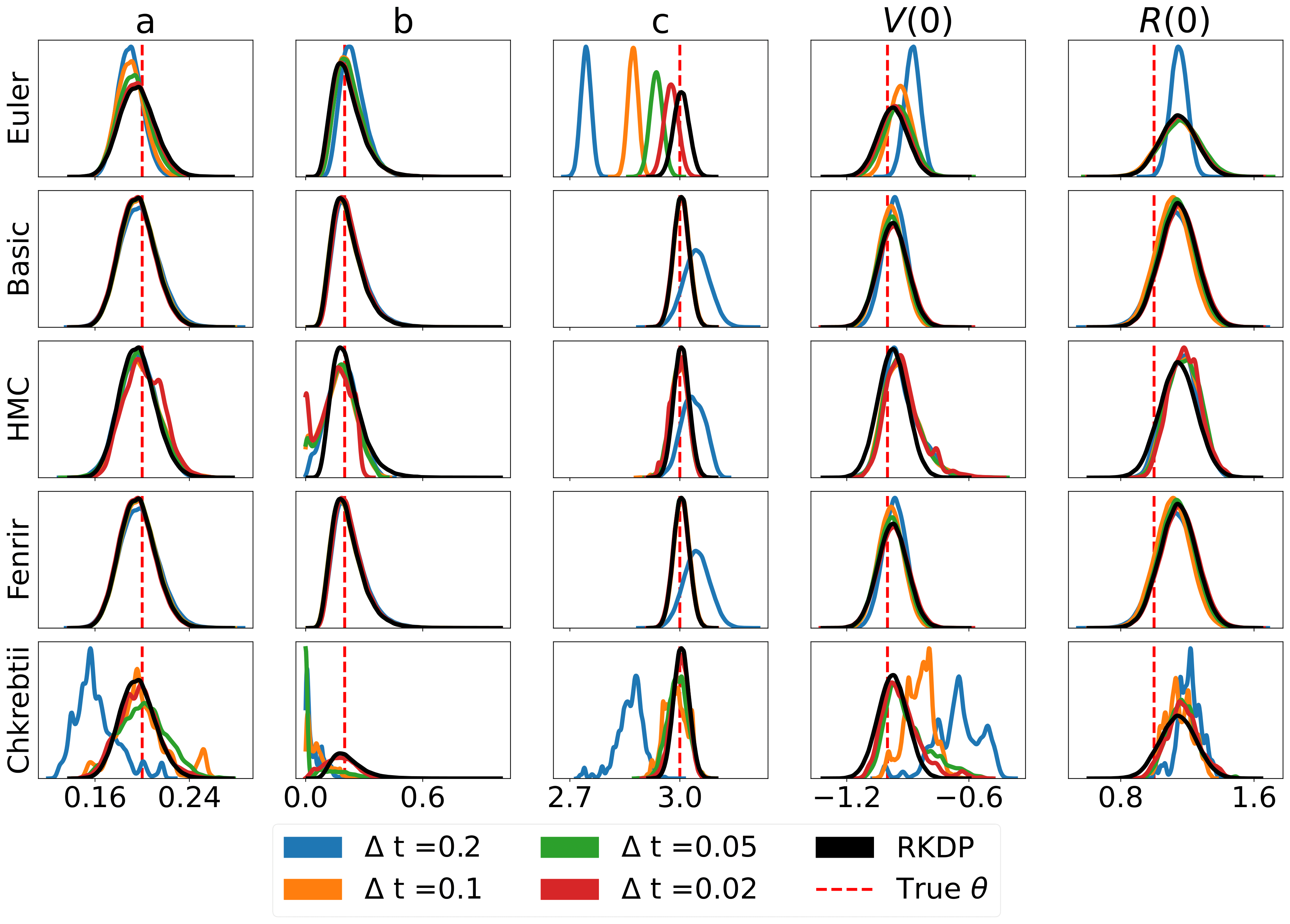
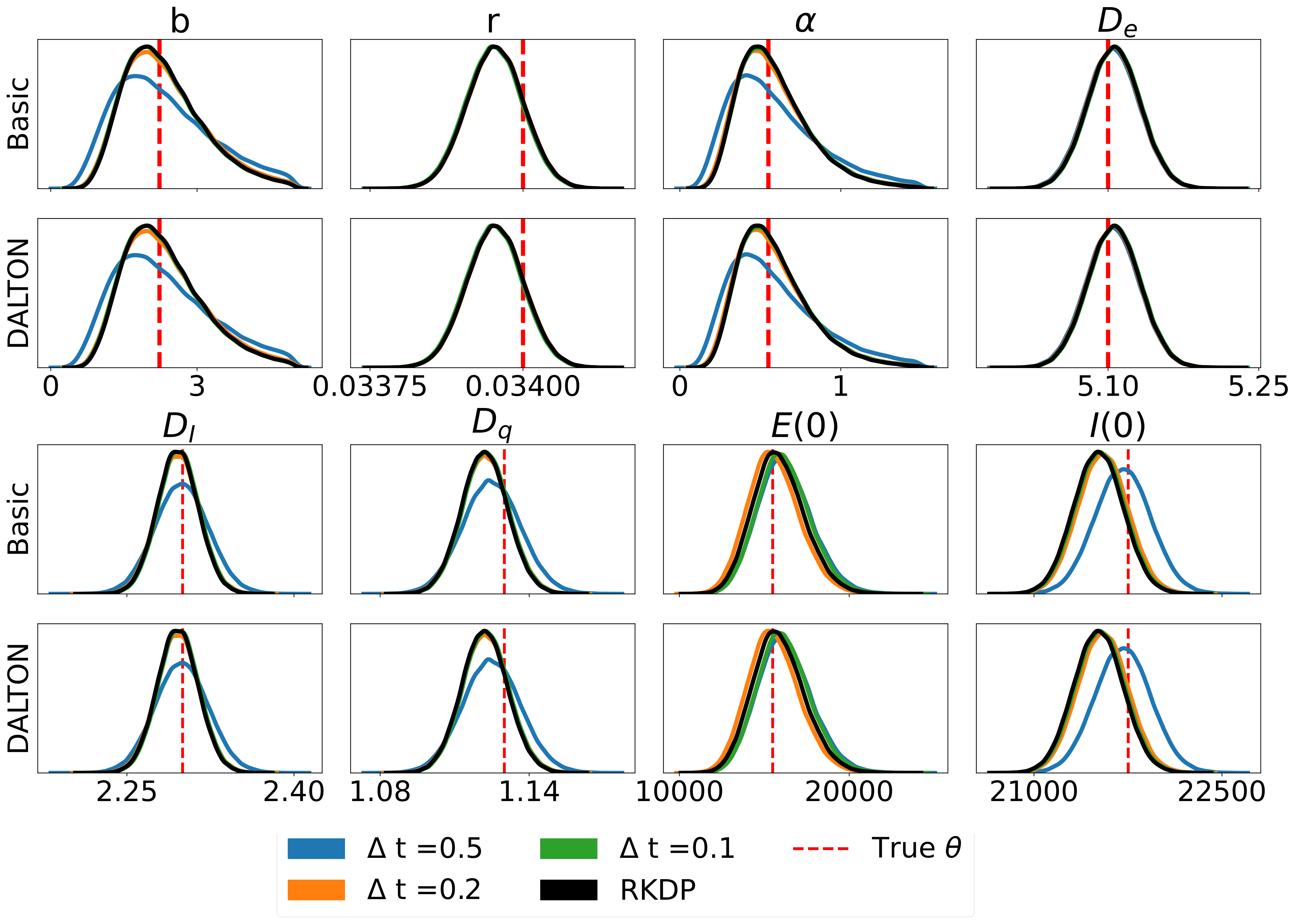
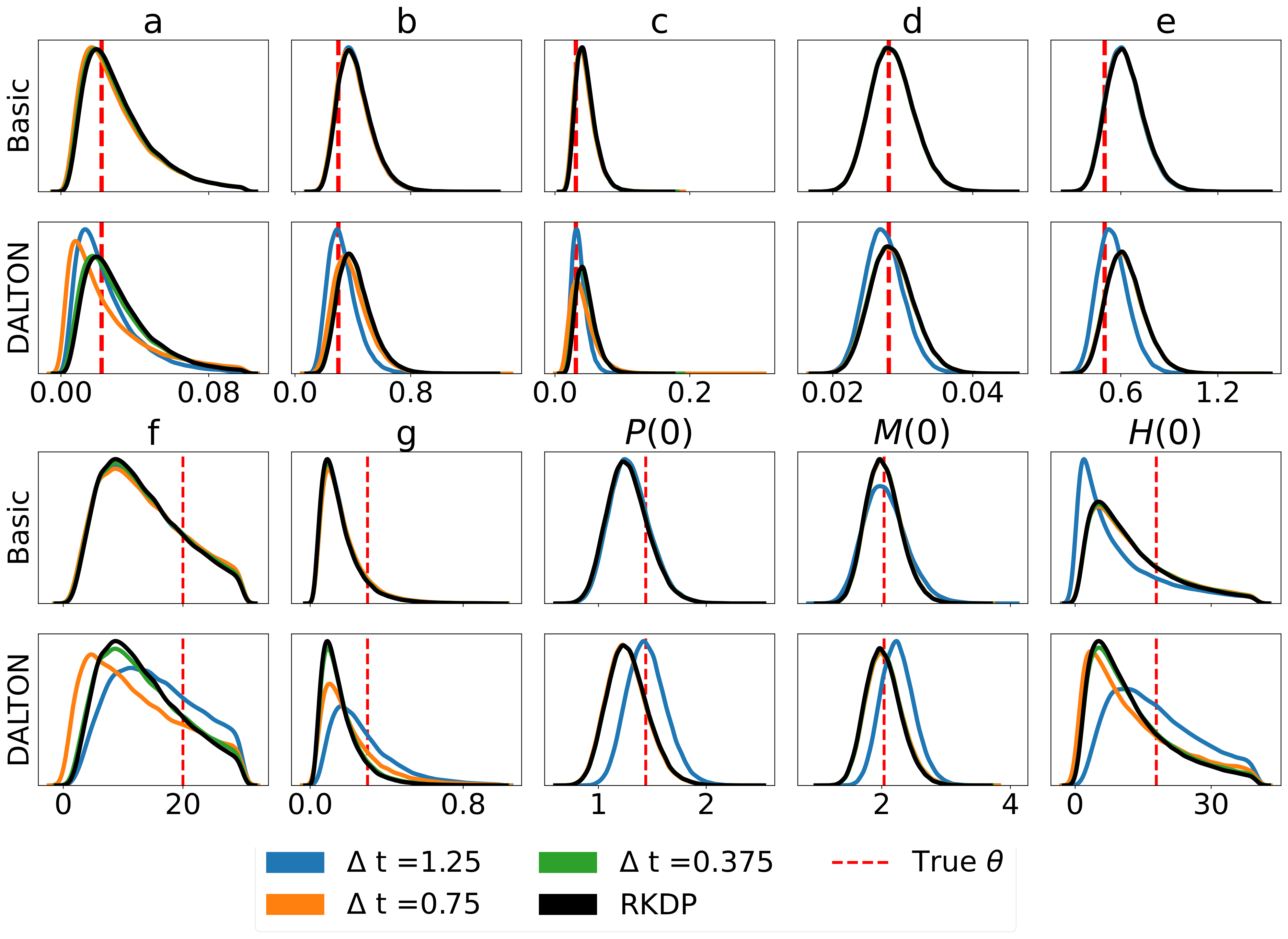
単体テストは次のコマンドで実行できます。
cd tests
python -m unittest discover -vまたは、 toxをインストールし、 rodeo内からコマンド ラインtoxを入力します。
HTML ドキュメントはルート フォルダーからコンパイルできます。
pip install .[docs]
cd docs
make htmlこれにより、 docs/buildにドキュメントが作成されます。