awesome latex drawing

素晴らしい LaTeX 描画

作成者: Xinyu Chen • https://xinychen.github.io

weawe-latex-drawing は、ベイジアン ネットワーク、関数プロット、グラフィカル モデル、テンソル構造、技術フレームワークなど、LaTeX を使用するための30 以上の学術的な描画サンプルのコレクションです。

説明

LaTeX は、無料ソフトウェアとして入手できる高品質の組版システムで、近年学術グラフィックの作成に広く使用されています。人気の理由は、特殊な記号や数式を使用した複雑なイラストを処理できるためで、研究で詳細なグラフィックを描画するのに最適です。

このプロジェクトでは、LaTeX を使用して作成されたいくつかのグラフィックスを、人気のあるオンライン LaTeX プラットフォームである Overleaf で簡単に理解できる例とともに紹介します。ご興味がございましたら、Overleaf.com (overleaf.com) で自由に例を調べて再現してください。

コンテンツ

例の表

• ベイジアンネットワーク
  • ベイジアン CP 分解のベイジアン ネットワーク (BCPF)
  • Bayesian Gaussian CP (BGCP) 分解のベイジアン ネットワーク
  • ベイジアン拡張テンソル因数分解 (BATF) のベイジアン ネットワーク
  • ベイジアン時間行列因数分解のベイジアン ネットワーク (BTMF)
  
  
• グラフィカルモデル
  • 部分的に観測された時系列行列とテンソル
  • 欠損値が存在する場合の行列およびテンソル時系列予測
  • 一定の次数をもつリレーショナル データ サンプル上の無向グラフと循環グラフ
  • ラプラシアン畳み込み時系列モデリング
  
  
• pgfplots関数のプロット
  • Erlang ディストリビューションの PDF および CDF 機能
  • さまざまな平均と分散を使用した正規分布の PDF
  • (共同)対数正規分布の PDF 関数
  • 連立一次方程式を解くための共役勾配の反復プロセス
  • ランダムおよび非ランダムの欠損パターン
  • サイン関数とコサイン関数
  • 時系列予測の仕組み
  
  
• マトリックス構造のtikz
  • 多変量時系列予測問題の図解
  • 時間行列分解の図解
  • 時間行列分解によるローリング時系列予測の図解
  
  
• テンソル構造のtikz-3dplot
  • (起点、宛先、タイムスロット) テンソルの図解
  • 3 次テンソルでの古典的な CP テンソル因数分解の図解
  • 拡張テンソル因数分解 (AuTF) モデルの図解
  • テンソル完了タスクとそのフレームワークの図解
  • 低ランク自己回帰テンソル完成モデルの図解
  • ユニタリ変換を使用したテンソル データの特異値しきい値処理の図解
  • 低ランクテンソル完成モデルの図解
  • 低ランクのテンソル回帰モデルの図解

ギャラリー

優れた LaTeX 描画サンプルをお探しですか?ここでは、LaTaX で描画する方法を示す 30 以上のグラフィックを示します。

ベイジアン ネットワーク

LaTeX は、柔軟なグラフィカル モデルを可能にする、強力なドメイン固有のパッケージとtikzなどのツールを提供します。ベイジアン ネットワークは、変数 (通常はノードで示される) と依存関係 (通常は矢印で示される) で構成されるグラフィカル モデルのファミリーを表します。幸いなことに、 tikzはベイジアン ネットワークと有向因子グラフを描画するための特別なライブラリがあります。

Python の別のツールボックス: https://docs.daft-pgm.org/en/latest/

ベイズ テンソル因数分解

【例1】

この例は次の論文からのものです。

• チャオ・キビン、チャン・リーチン、アンジェイ・チチョッキ（2015）。自動ランク決定による不完全テンソルのベイジアン CP 分解。パターン分析とマシン インテリジェンスに関する IEEE トランザクション、37(9): 1751-1763。

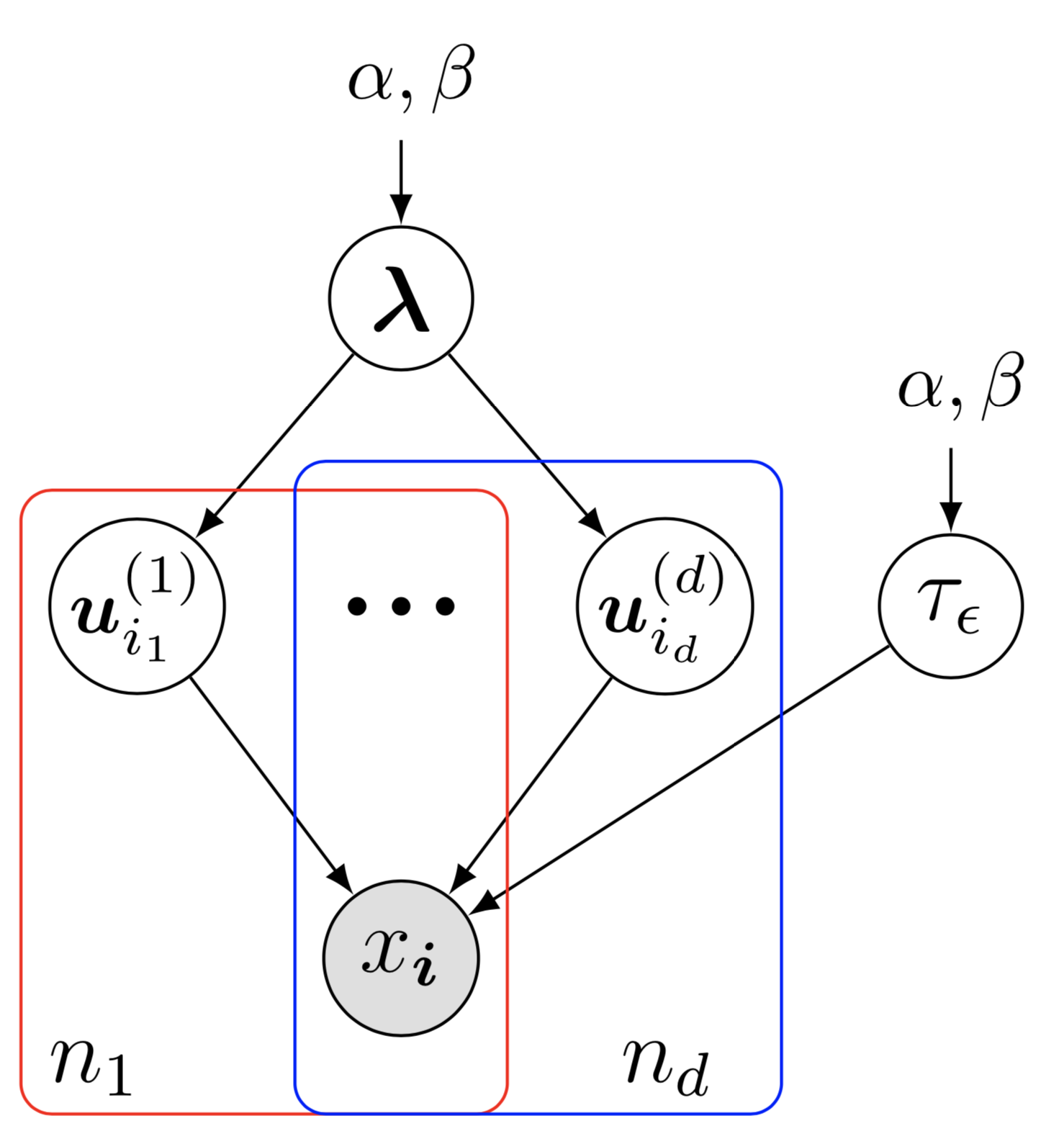これは、ベイジアン CP 分解のベイジアン ネットワーク (BCPF) モデルを示しています。このベイジアン ネットワークの例を描くには、次のような準備が必要です。

• preambleコード:
  1. documentclass standaloneとして定義します。たとえば、 documentclass[border = 0.1cm]{standalone}で 0.1cm の境界線を持ちます。
  2. パッケージtikz 、つまりusepackage{tikz}を使用し、ベイジアン ネットワークと有向因子グラフを描画するための重要なツールであるusetikzlibrary{bayesnet}のようなtikzライブラリを使用します。
  3. tikzstyle{}コマンドを使用してtikzスタイルを設定します。
  4. usepackage{amsfonts, amsmath, amssymb}を含む数式環境を使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してベイジアン ネットワーク内のノードとテキスト ボックスを定義します。
  3. path使用してベイジアン ネットワーク内の矢印を定義します。
  4. plate使用してベイジアン ネットワークでプレートを定義します。

画像をクリックしてソースコードを確認してください。

• オーバーリーフ プロジェクトで BGCP.tex を開くと、ベイジアン ネットワークとしての BGCP (ベイジアン ガウス CP 分解) モデルと有向因子グラフに関する次の図が表示されます。

【例2】

この例は次の論文からのものです。

チェン・シンユー、何・ジャオチェン、スン・リージュン（2019）。時空間トラフィック データ代入のためのベイジアン テンソル分解アプローチ。交通研究パート C: 新興技術、98: 73-84。

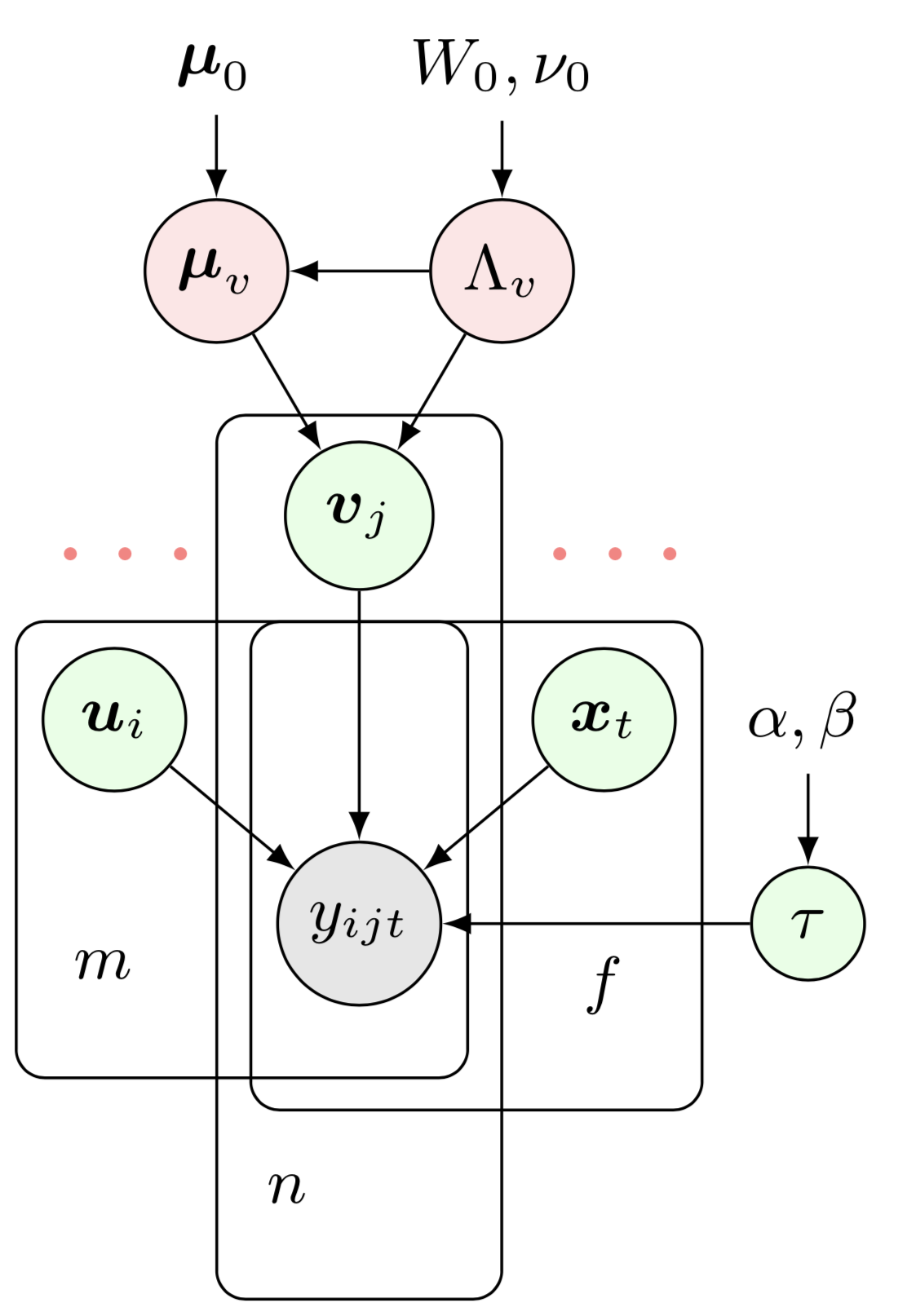これは、ベイジアン ガウス CP 分解 (BGCP) モデルのベイジアン ネットワークを示しています。このベイジアン ネットワークの例を描くには、次のような準備が必要です。

• preambleコード:
  1. documentclass standaloneとして定義します。たとえば、 documentclass[border = 0.1cm]{standalone}で 0.1cm の境界線を持ちます。
  2. パッケージtikz 、つまりusepackage{tikz}を使用し、ベイジアン ネットワークと有向因子グラフを描画するための重要なツールであるusetikzlibrary{bayesnet}のようなtikzライブラリを使用します。
  3. tikzstyle{}コマンドを使用してtikzスタイルを設定します。
  4. usepackage{amsmath, amsfonts, amssymb}を含む数式環境を使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してベイジアン ネットワーク内のノードとテキスト ボックスを定義します。
  3. path使用してベイジアン ネットワーク内の矢印を定義します。
  4. plate使用してベイジアン ネットワークでプレートを定義します。

画像をクリックしてソースコードを確認してください。論文中の BGCP のオリジナルのベイジアン ネットワークに興味がある場合は、BGCP.tex をチェックしてください。

【例3】

この例は次の論文からのものです。

Xinyu Chen、Zhaocheng He、Yixian Chen、Yuhuan Lu、Jiawe Wang (2019)。ベイジアン拡張テンソル因数分解モデルを使用した、欠落しているトラフィック データの代入とパターンの発見。交通研究パート C: 新興技術、104: 66-77。

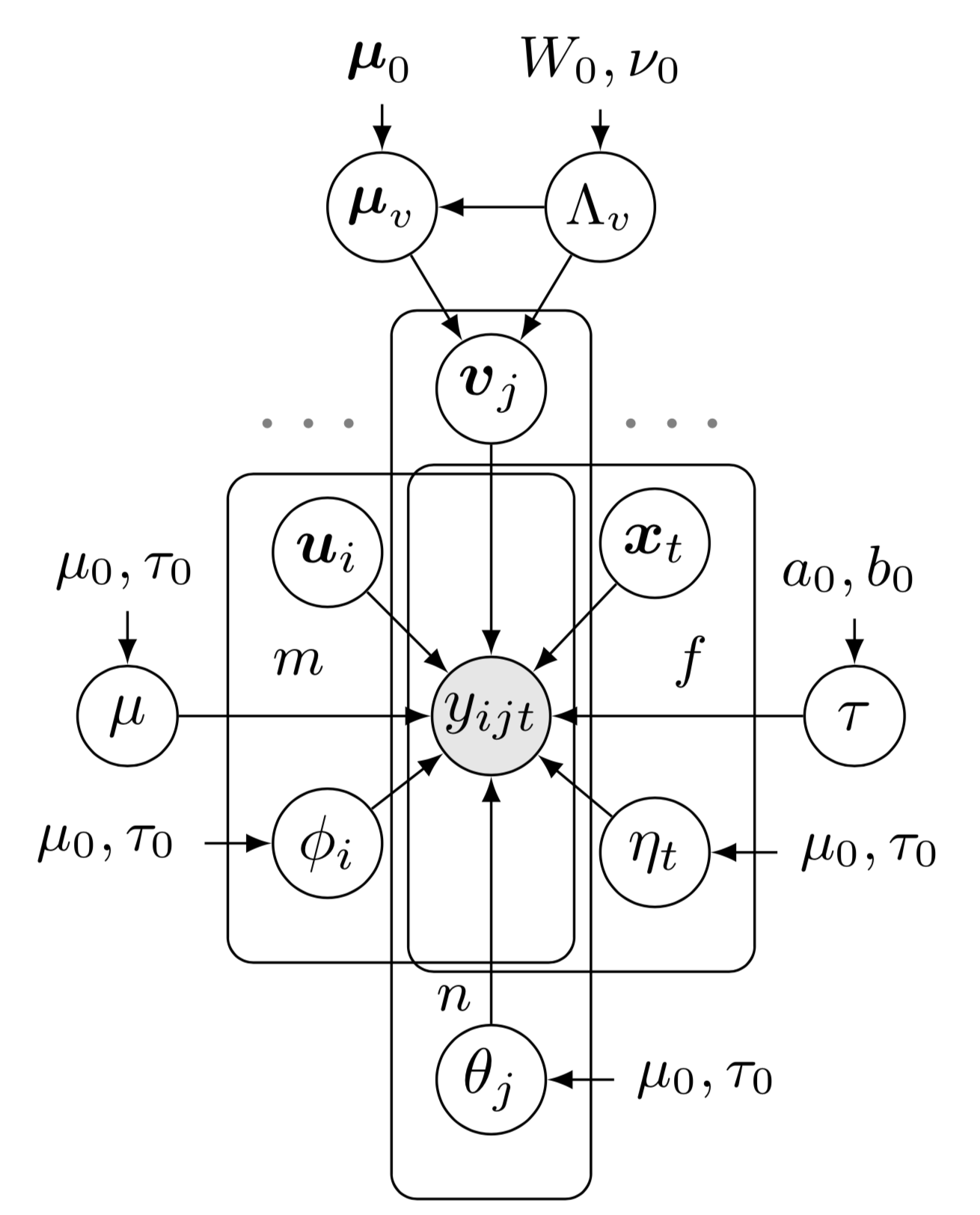これは、ベイジアン拡張テンソル因数分解 (BATF) モデルのベイジアン ネットワークを示しています。このベイジアン ネットワークの例を描くには、次のような準備が必要です。

• preambleコード:
  1. documentclass standaloneとして定義します。たとえば、 documentclass[border = 0.1cm]{standalone}で 0.1cm の境界線を持ちます。
  2. パッケージtikz 、つまりusepackage{tikz}を使用し、ベイジアン ネットワークと有向因子グラフを描画するための重要なツールであるusetikzlibrary{bayesnet}のようなtikzライブラリを使用します。
  3. tikzstyle{}コマンドを使用してtikzスタイルを設定します。
  4. usepackage{amsmath, amsfonts, amssymb}を含む数式環境を使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してベイジアン ネットワーク内のノードとテキスト ボックスを定義します。
  3. path使用してベイジアン ネットワーク内の矢印を定義します。
  4. plate使用してベイジアン ネットワークでプレートを定義します。

画像をクリックしてソースコードを確認してください。

【例4】

この例は次の論文からのものです。

チェン・シンユー、スン・リージュン（2021）。多次元時系列予測のためのベイズ時間因数分解。パターン分析とマシン インテリジェンスに関する IEEE トランザクション、44 (9): 4659-4673。

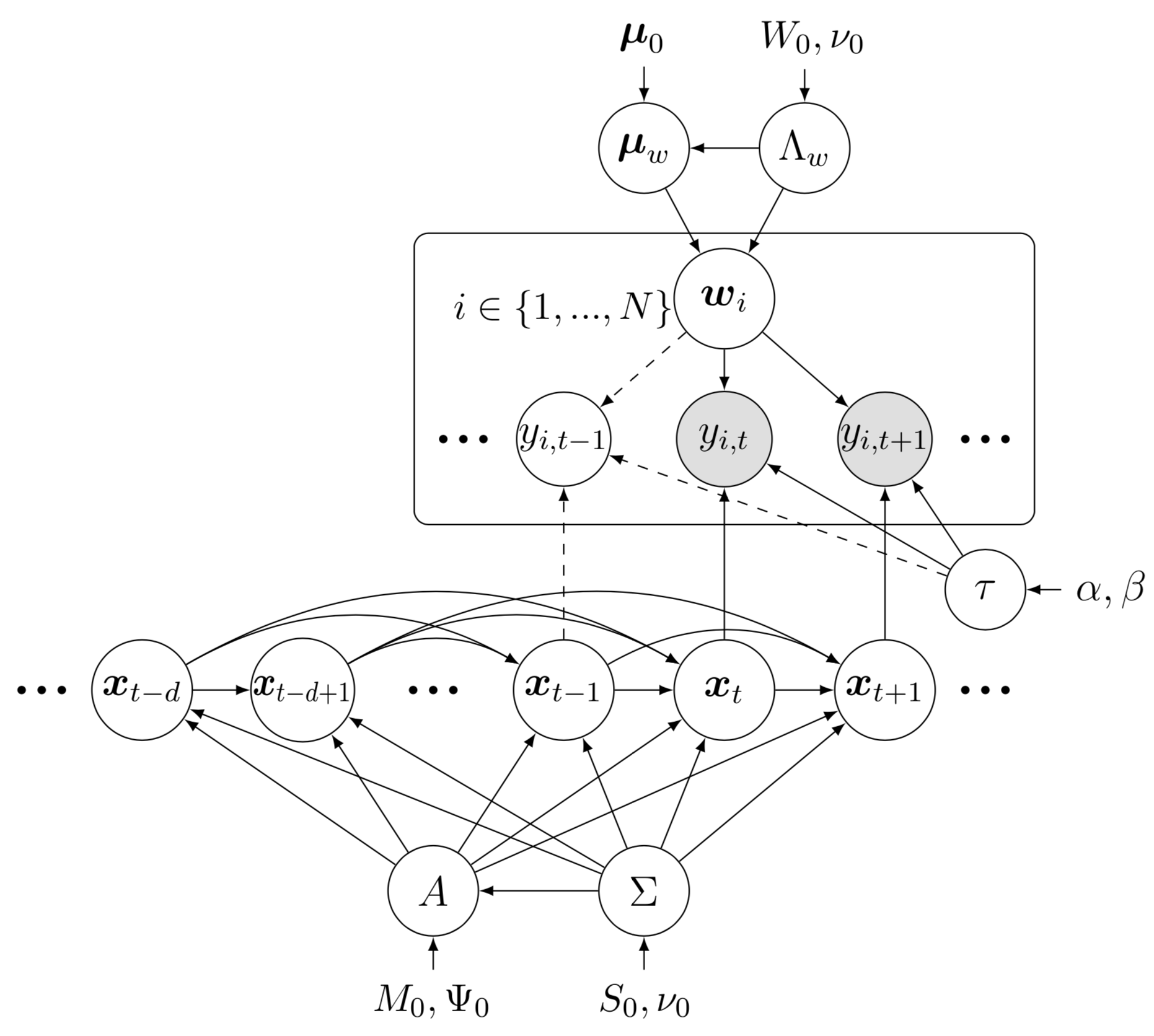これは、ベイジアン時間行列因数分解 (BTMF) モデルのベイジアン ネットワークを示しています。このベイジアン ネットワークの例を描くには、次のような準備が必要です。

• preambleコード:
  1. documentclass standaloneとして定義します。たとえば、 documentclass[border = 0.1cm]{standalone}で 0.1cm の境界線を持ちます。
  2. パッケージtikz 、つまりusepackage{tikz}を使用し、ベイジアン ネットワークと有向因子グラフを描画するための重要なツールであるusetikzlibrary{bayesnet}のようなtikzライブラリを使用します。
  3. tikzstyle{}コマンドを使用してtikzスタイルを設定します。
  4. usepackage{amsmath, amsfonts, amssymb}を含む数式環境を使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してベイジアン ネットワーク内のノードとテキスト ボックスを定義します。
  3. path使用してベイジアン ネットワーク内の矢印を定義します。
  4. plate使用してベイジアン ネットワークでプレートを定義します。

画像をクリックしてソースコードを確認してください。時間因子に対する多変量ベクトル自己回帰プロセスの代わりに、単変量自己回帰プロセスを使用して BTMF を再構築することもできます。 Beyasian ネットワークは btmf_net.png で入手でき、ソース コード btmf_net.tex もチェックアウトできます。

グラフィカルモデル

【例5】

これら 2 つの例は、それぞれ部分的に観察された時系列行列とテンソルを示しています。 2 つの例の両方を描画するには、次の手順に従います。

• preambleコード:

  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。

• bodyコード:

  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してグラフィカル モデル内のノードとテキスト ボックスを定義します。
  3. path使用してグラフィカル モデル内の矢印を定義します。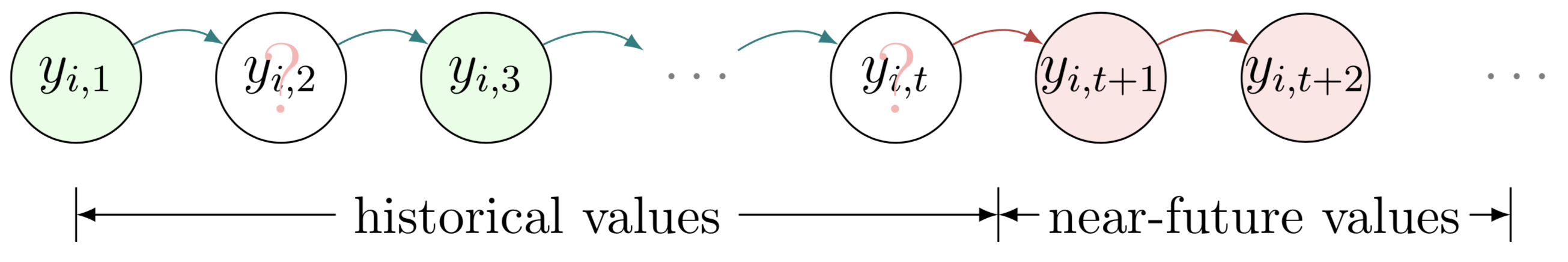

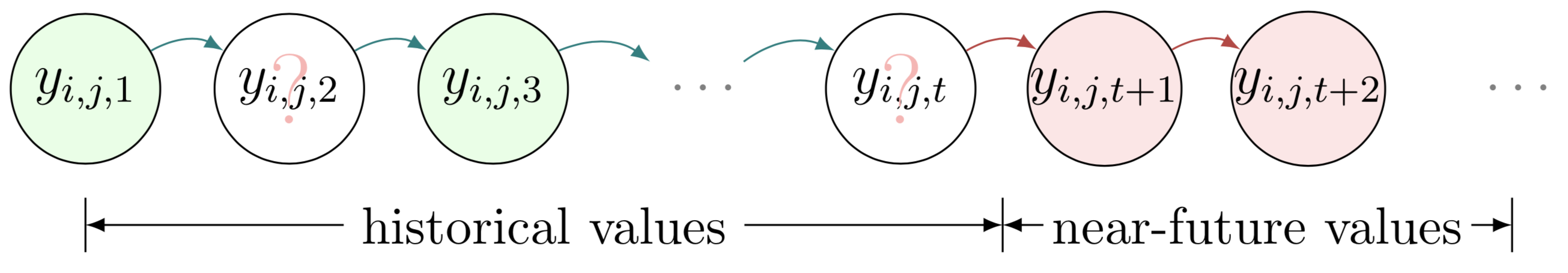
【例6】

これら 2 つの例は、欠損値が存在する場合の時系列予測を示しています。 2 つの例の両方を描画するには、次の手順に従います。

• preambleコード:

  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。

• bodyコード:

  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してグラフィカル モデル内のノードとテキスト ボックスを定義します。
  3. path使用してグラフィカル モデル内の矢印を定義します。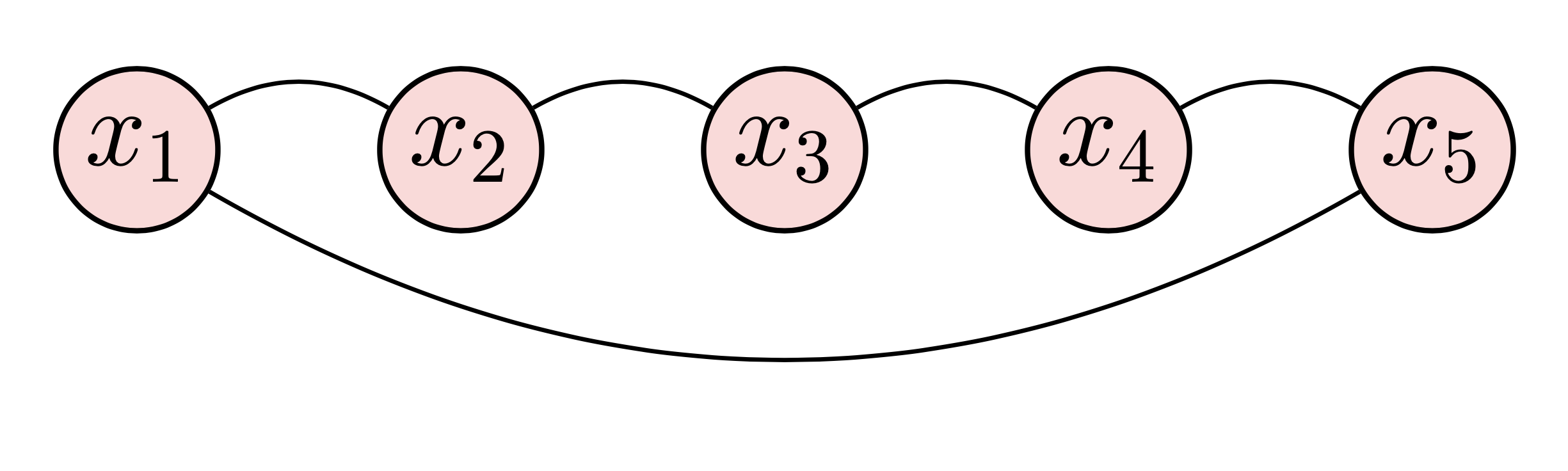

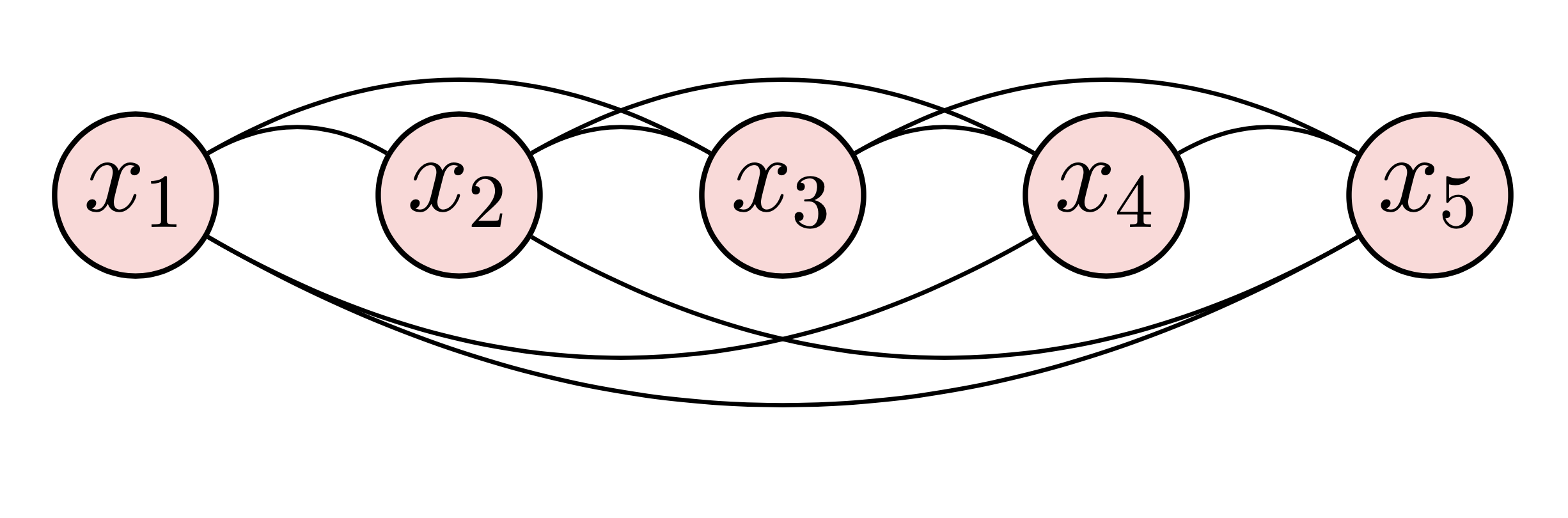
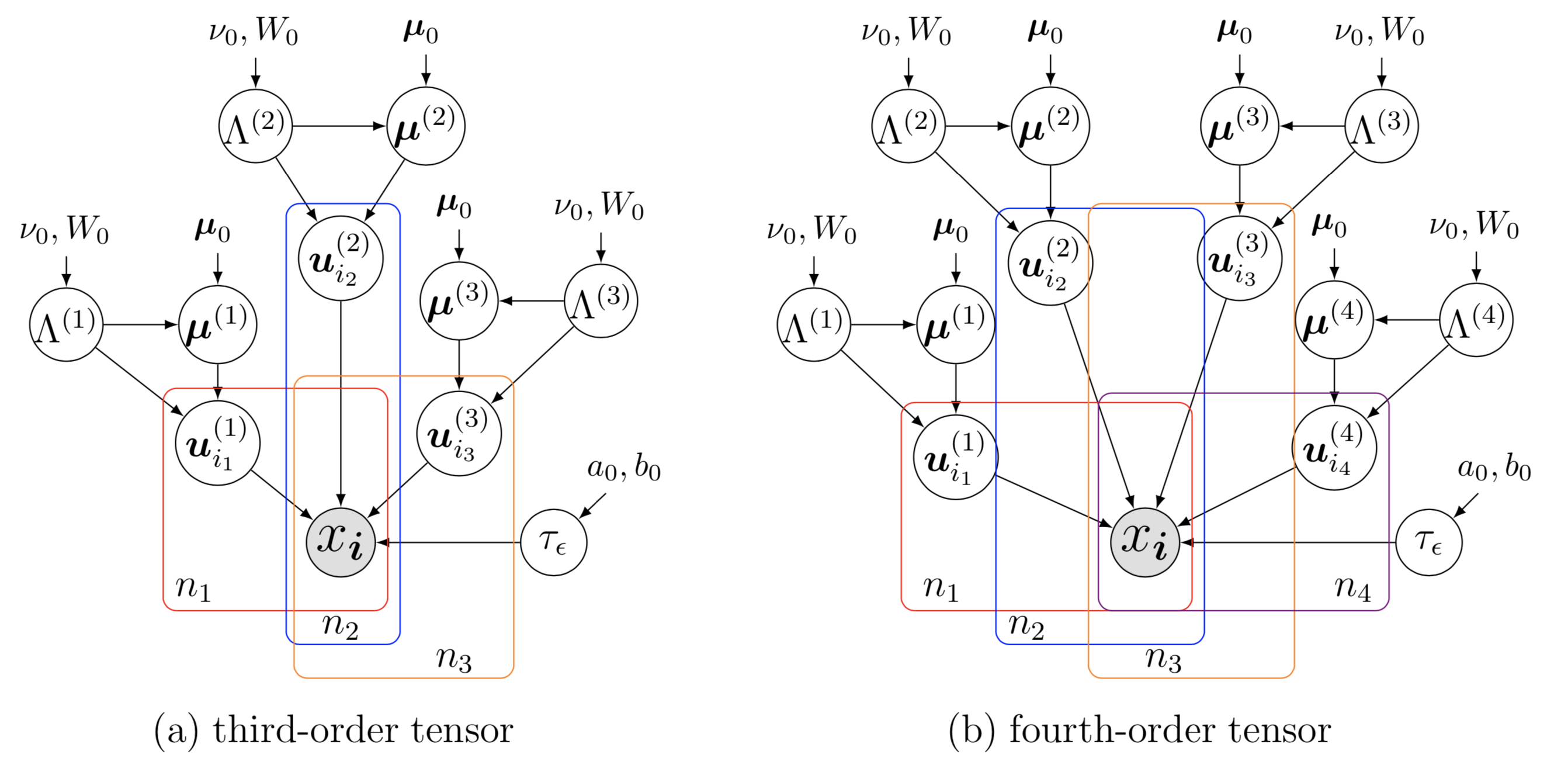
【例7】

これら 2 つの例は、特定の次数のリレーショナル データ サンプルに関する無向グラフと循環グラフを示しています。 2 つの例の両方を描画するには、次の手順に従います。

• preambleコード:

  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。

• bodyコード:

  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. node使用してノードを定義します。
  3. path使用して矢印を定義します。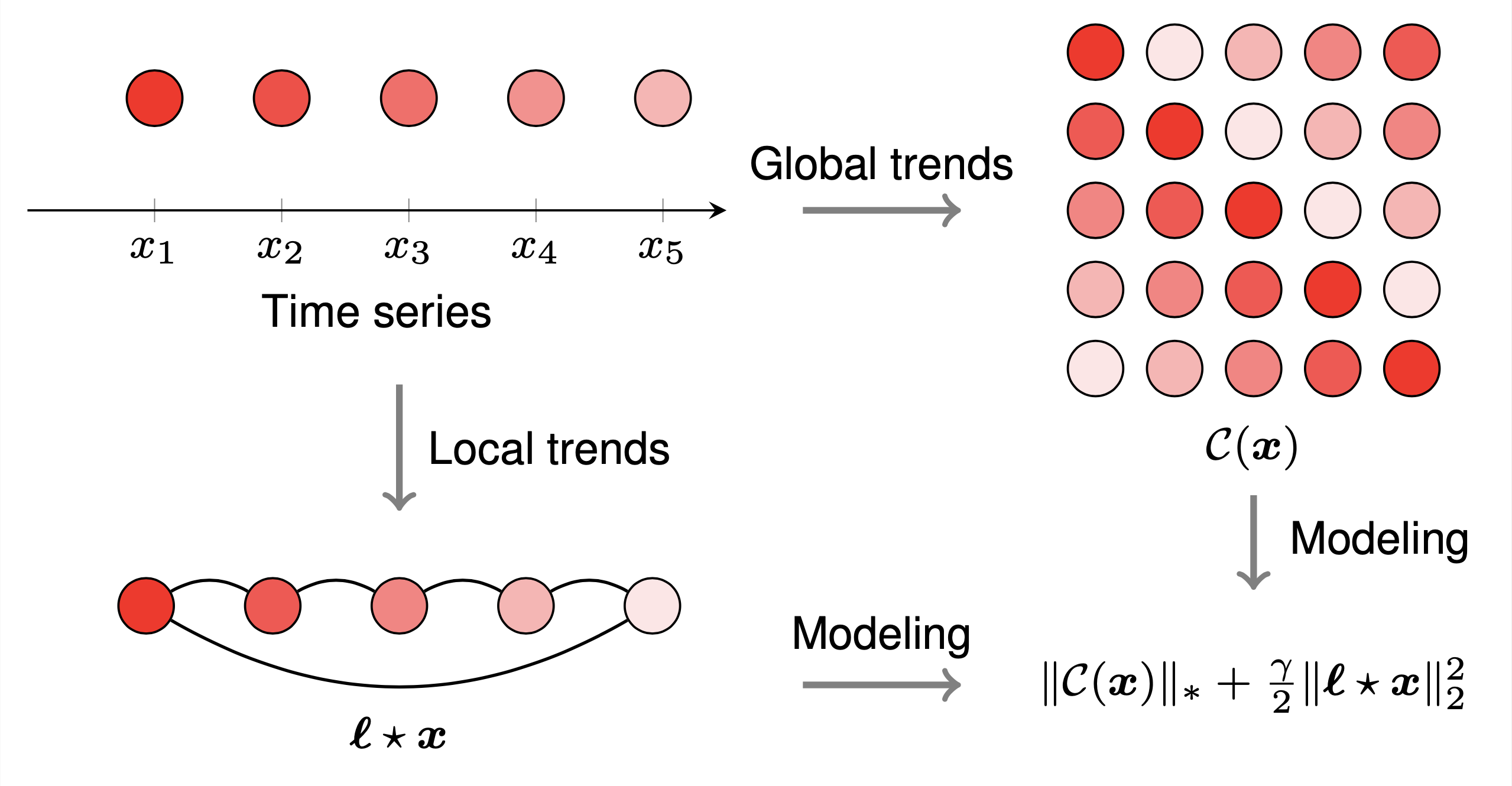

【例8】

この例は次の論文からのものです。

Xinyu Chen、Zhanhong Cheng、Nicolas Saunier、Lijun Sun (2022)。交通時系列補完のラプラシアン畳み込み表現。 arXiv プレプリント arXiv: 2212.01529。

これは、時系列補完のためのラプラシアン畳み込みモデルを図示したものです。例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. begin{axis} end{axis}とaddplot使用して座標を描画します。
  3. nodeとpath使用してノードと矢印を描画します。

pgfplots関数のプロット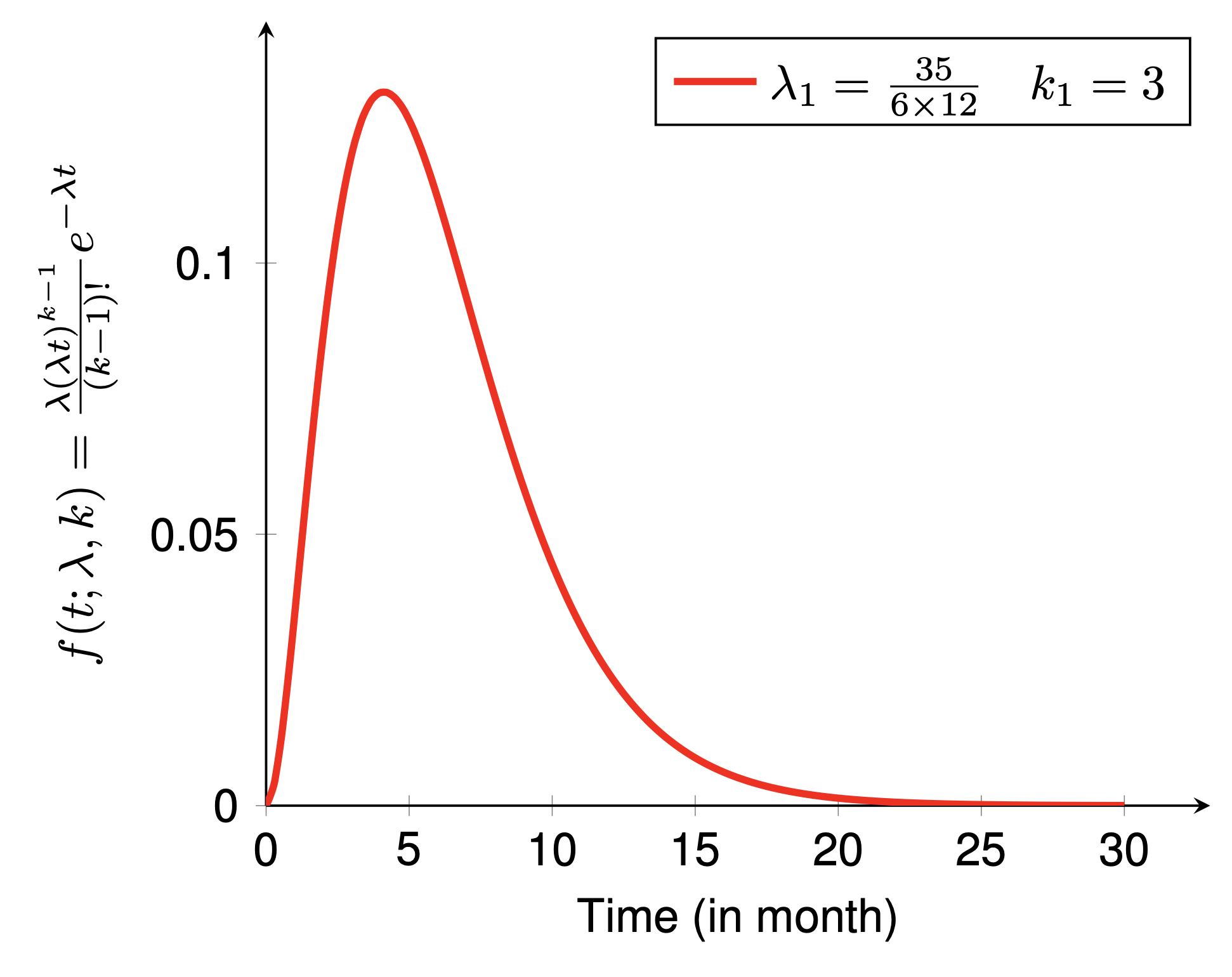

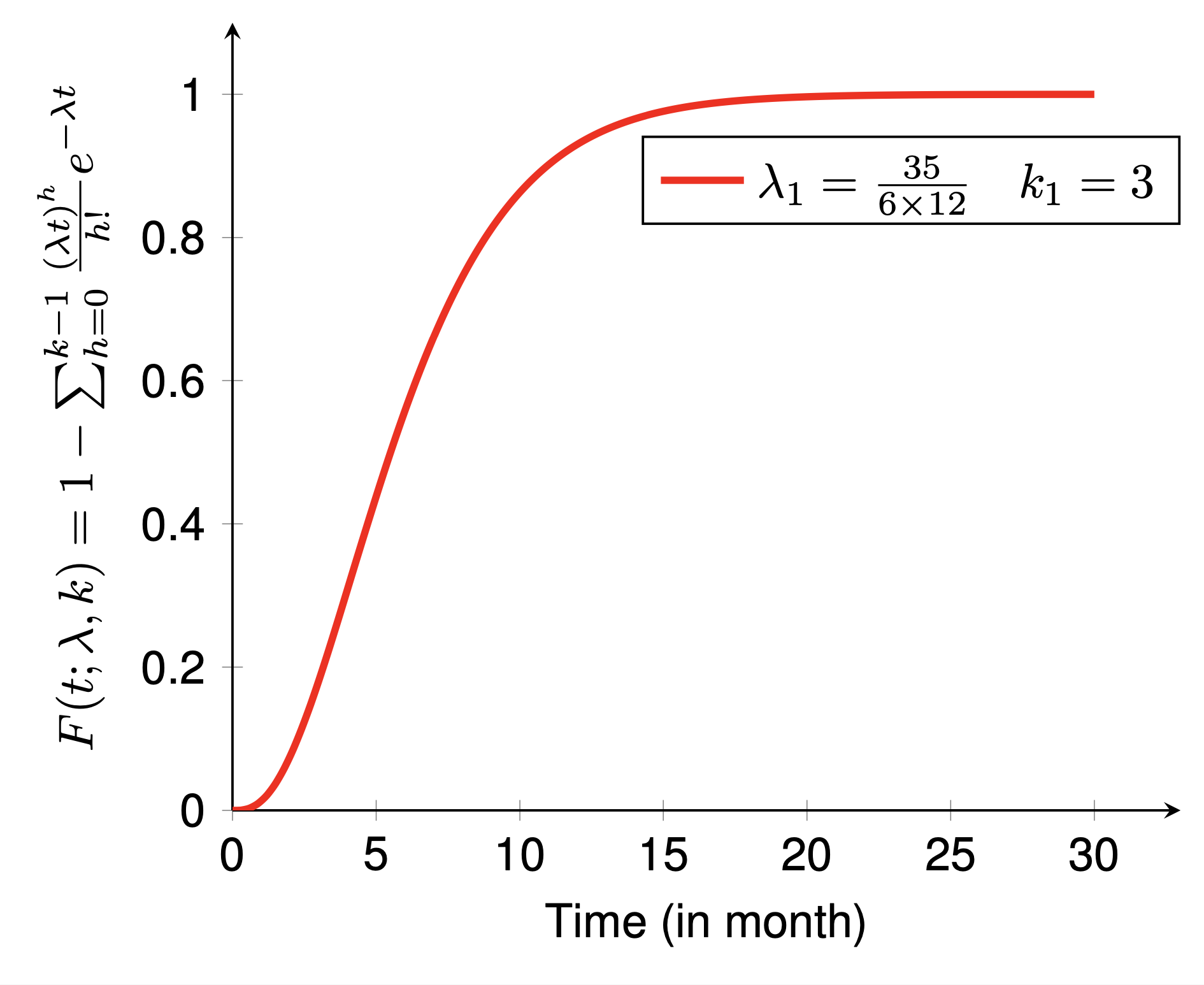
【例9】

これら 2 つの例は、それぞれ Erlang 分布の確率密度関数 (PDF) と累積密度関数 (CDF) を示しています。この例を描くには、いくつかの手順に従う必要があります。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. pgfplotsパッケージを使用します。
  3. フォント スタイルを設定し、必要に応じてpgfplotsset{}を調整します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. begin{axis} end{axis}を使用して関数を描画します。
  3. addplot使用して描画用の関数を定義します。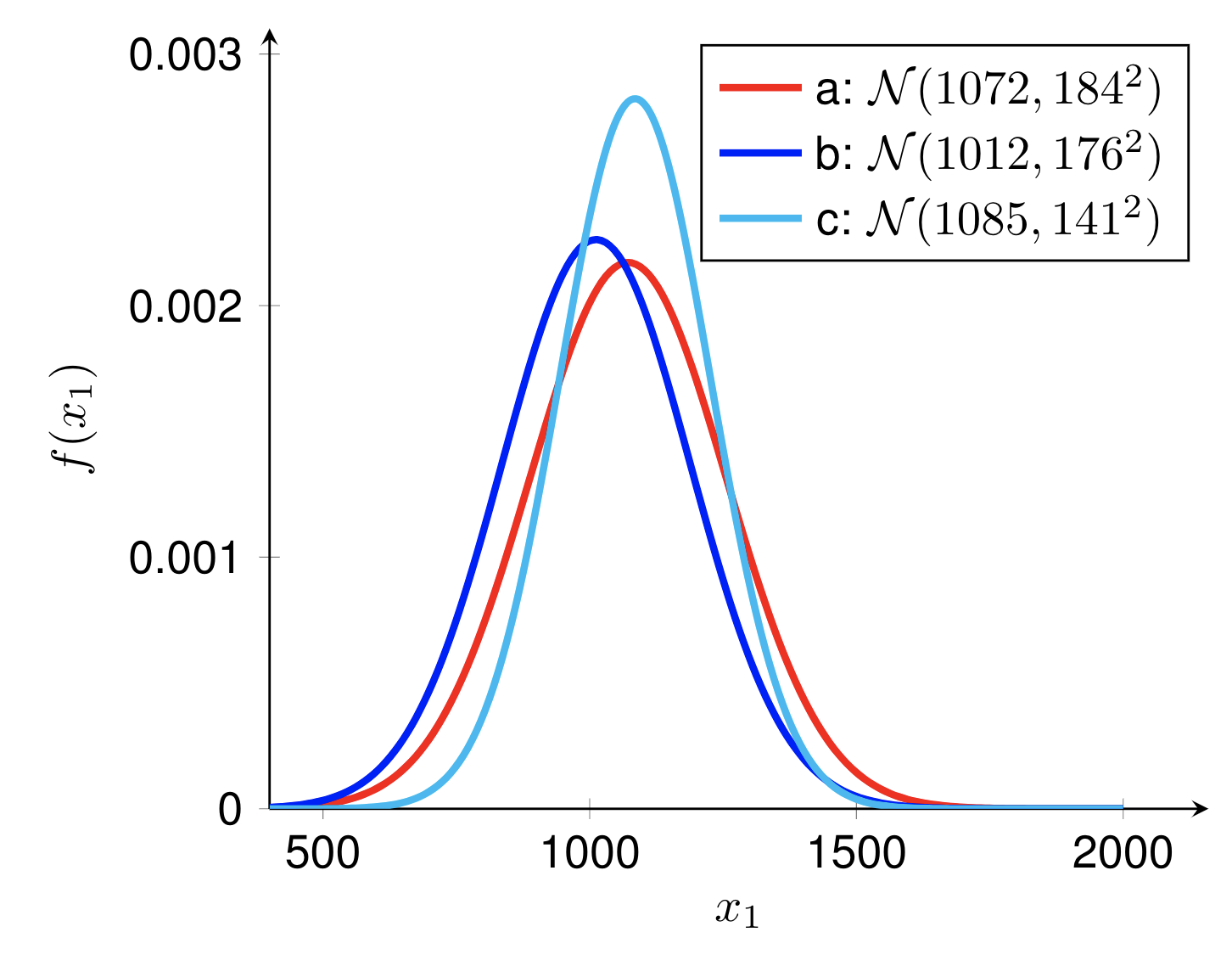

【例10】

この例では、さまざまな平均と分散を使用した正規分布の PDF を示します。この例を描画するには、いくつかの手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. pgfplotsパッケージを使用します。
  3. フォント スタイルを設定し、必要に応じてpgfplotsset{}を調整します。
• bodyコード:
  1. pgfmathdeclarefunctionを使用して正規 (ガウス) 分布の PDF 関数を定義します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. begin{axis} end{axis}を使用して関数を描画します。
  4. addplot使用して描画用の関数を定義します。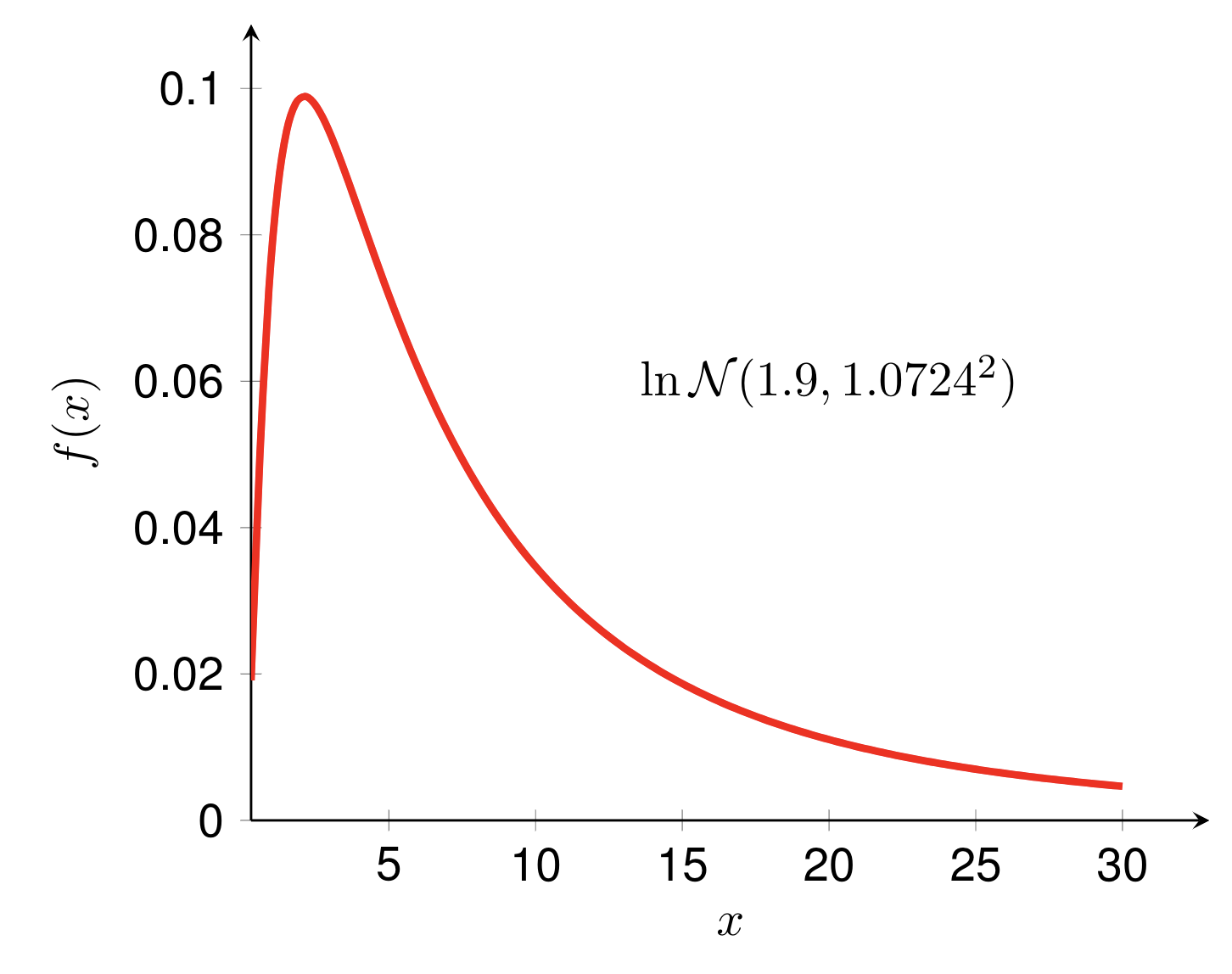
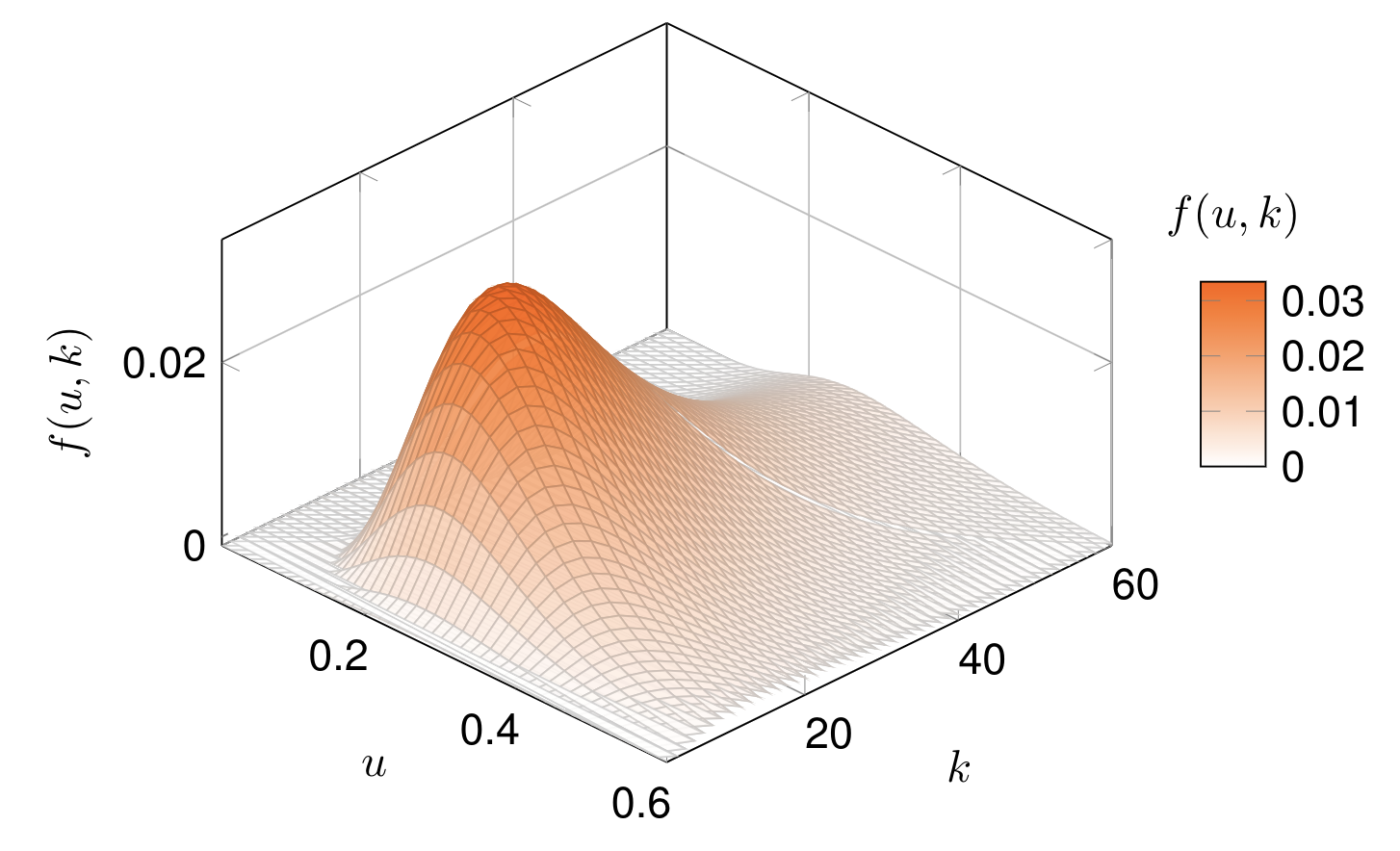
• 他の投稿:
  1. pgfplots での正規分布のプロット
  2. pgfplots 軸の数値形式
  3. 不合理な科学表記を削除する

【例11】

これら 2 つの例は、それぞれ対数正規分布の PDF と結合 PDF を示しています。例に従うために推奨される資料がいくつかあります。

• 他の投稿:
  1. TikZで二変量正規分布を描く
  2. 2 つの二変量正規分布を 1 つのプロットにプロットするにはどうすればよいでしょうか?
  3. Tikz での二変量正規分布のプロット
  4. addplot3 で曲線を分割する

【例12】

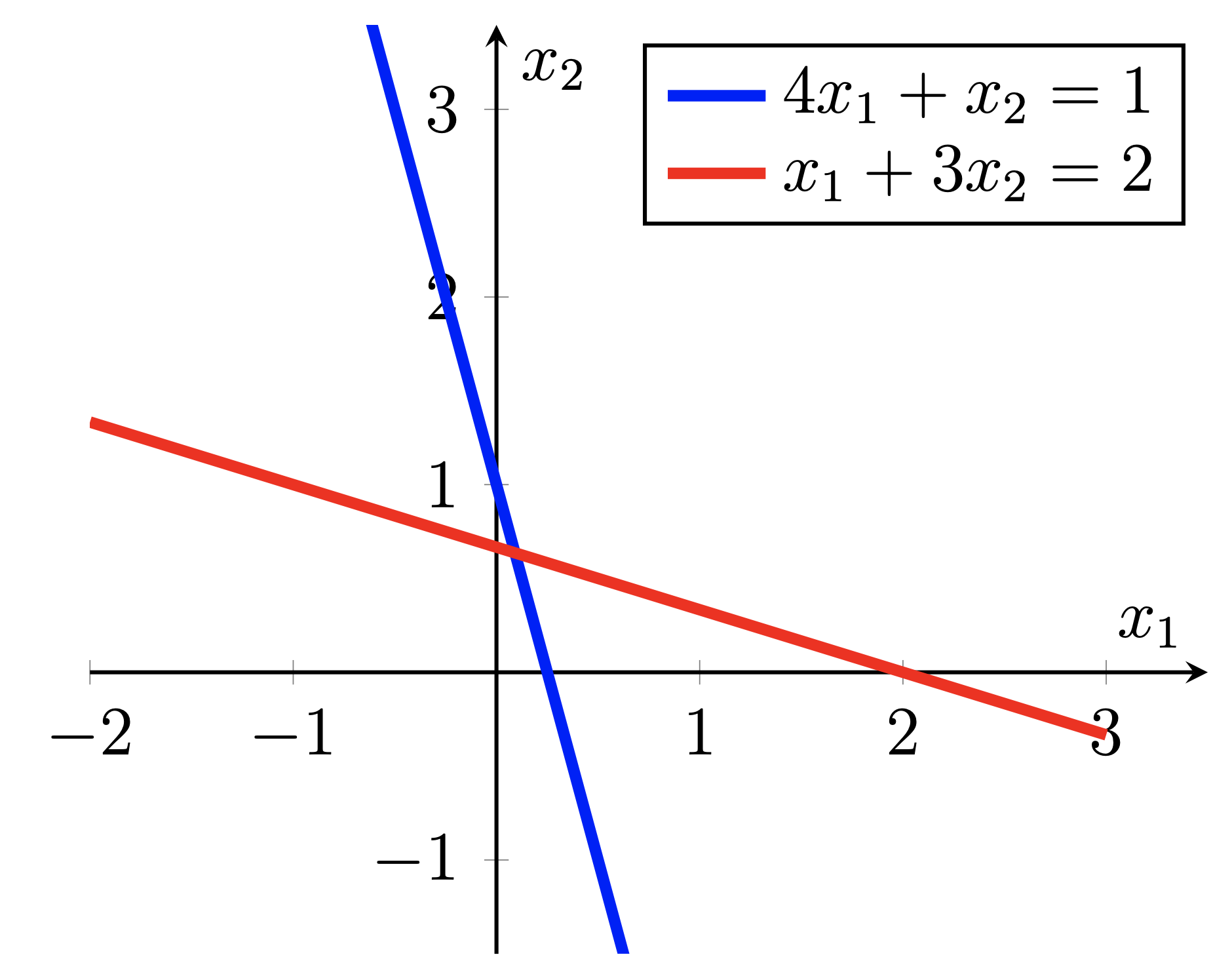
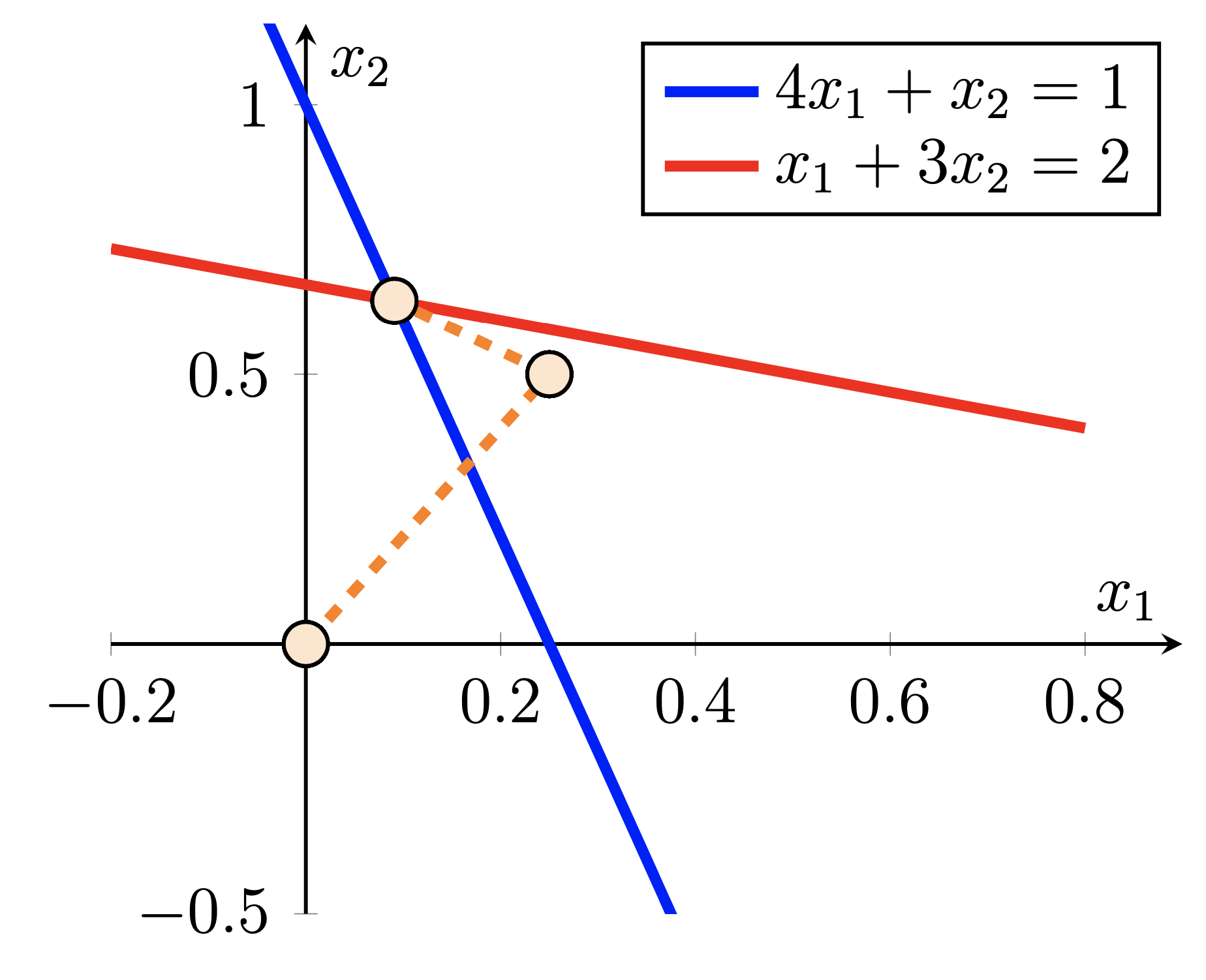
これら 2 つの例は、連立一次方程式を解くための共役勾配の反復プロセスを示しています。

【例13】

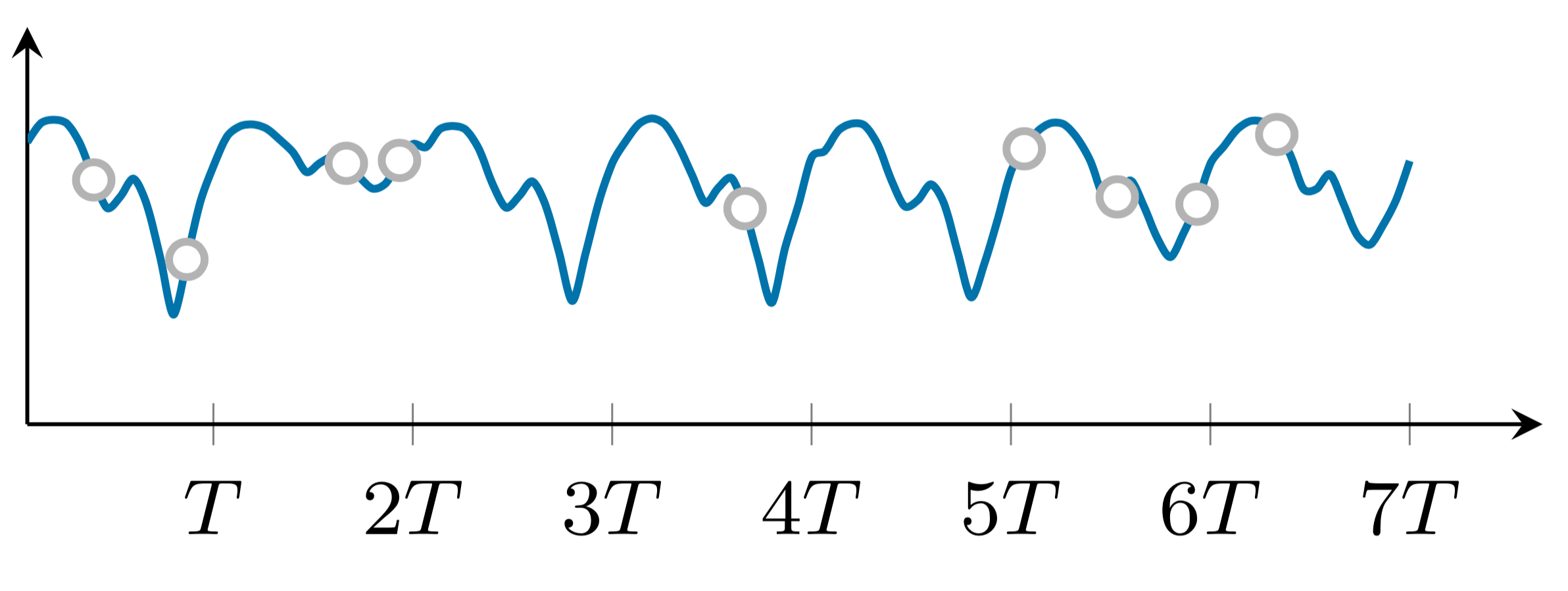
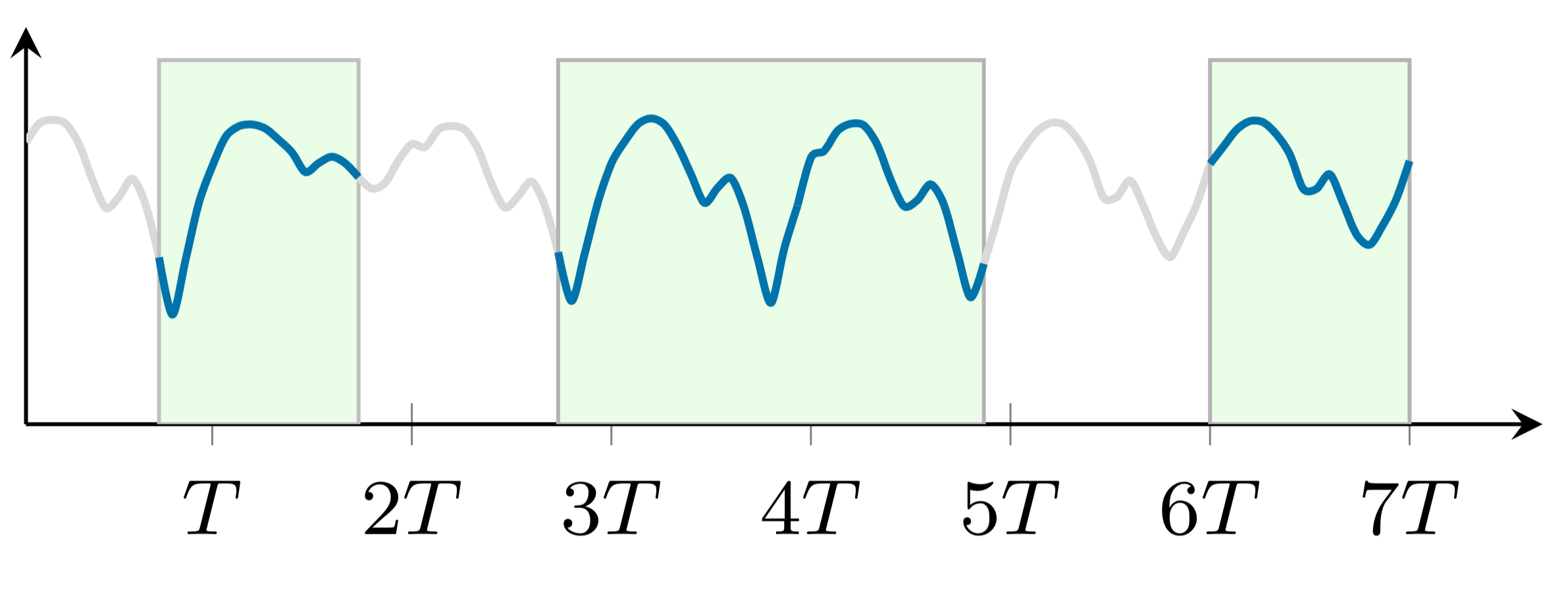
これら 2 つの例は、ランダムな欠損パターンと非ランダムな欠損パターンを示しています。 2 つの例の両方を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzパッケージとpgfplotsパッケージの両方を使用します。
  3. begin{filecontents} end{filecontents}を使用してデータを含めます。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. begin{axis} end{axis}を使用して関数を描画します。
  3. addplot使用してデータを描画します。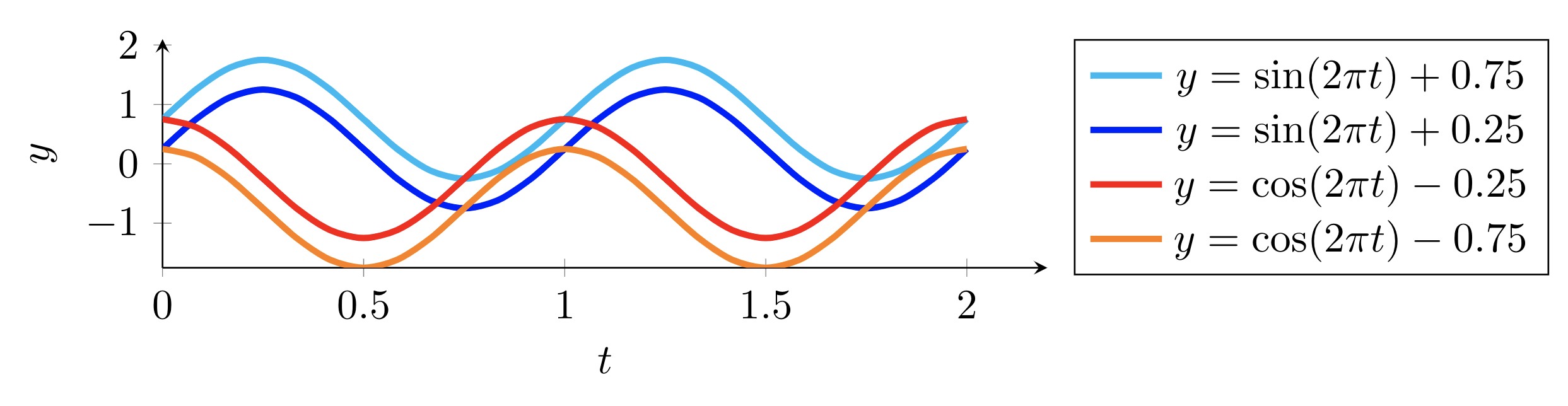

【例14】

この例では、サイン関数とコサイン関数で構成される 4 つのシーケンスを示します。これらのシーケンスを時系列として考えると、2 種類の時間ダイナミクスがわかります。1 つはサイン関数によるもの、もう 1 つはコサイン関数によるものです。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. pgfplotsパッケージを使用します。
  3. フォント スタイルを設定し、必要に応じてpgfplotsset{}を調整します。
• bodyコード:
  1. pgfmathdeclarefunctionを使用して正規 (ガウス) 分布の PDF 関数を定義します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. begin{axis} end{axis}を使用して関数を描画します。
  4. addplot使用して描画用の関数を定義します。

【例15】

この例では、Tracebase プロジェクトのストリーミング データに対する時系列予測のメカニズムを示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzパッケージとpgfplotsパッケージの両方を使用します。
  3. フォント スタイルを設定し、必要に応じてpgfplotsset{}を調整します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. begin{axis} end{axis}を使用してグラフィックを定義します。
  3. addplot使用して、いくつかの座標でマークを定義し、これらのマークの色を指定します。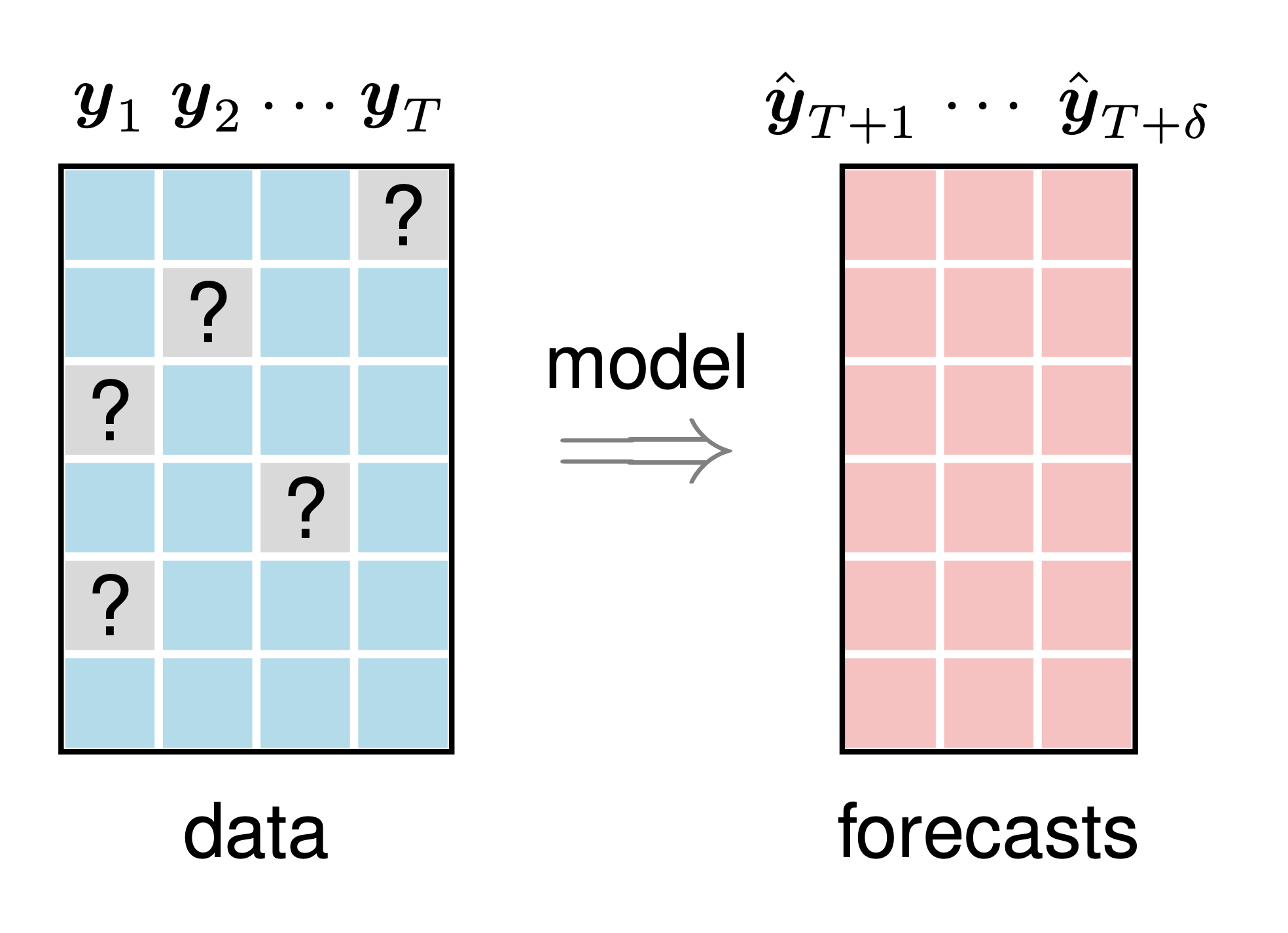

マトリックス構造のtikz

【例16】

この例では、欠損値を含む多変量時系列予測問題をグラフィカルに示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. draw 、 filldraw 、およびnodeコマンドを使用して、四角形とノードを定義します。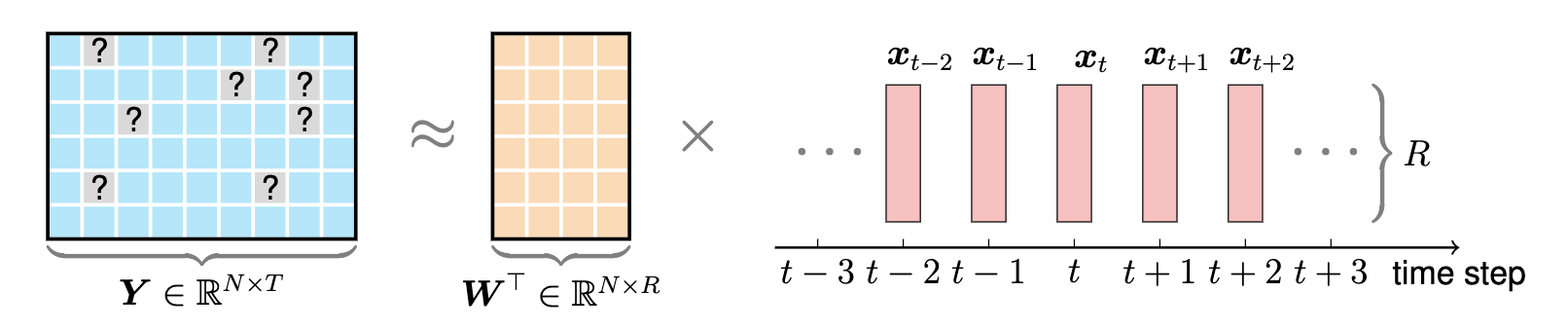

【例17】

この例では、時間行列分解をグラフで示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. drawとfilldraw使用してノードと四角形を設定します。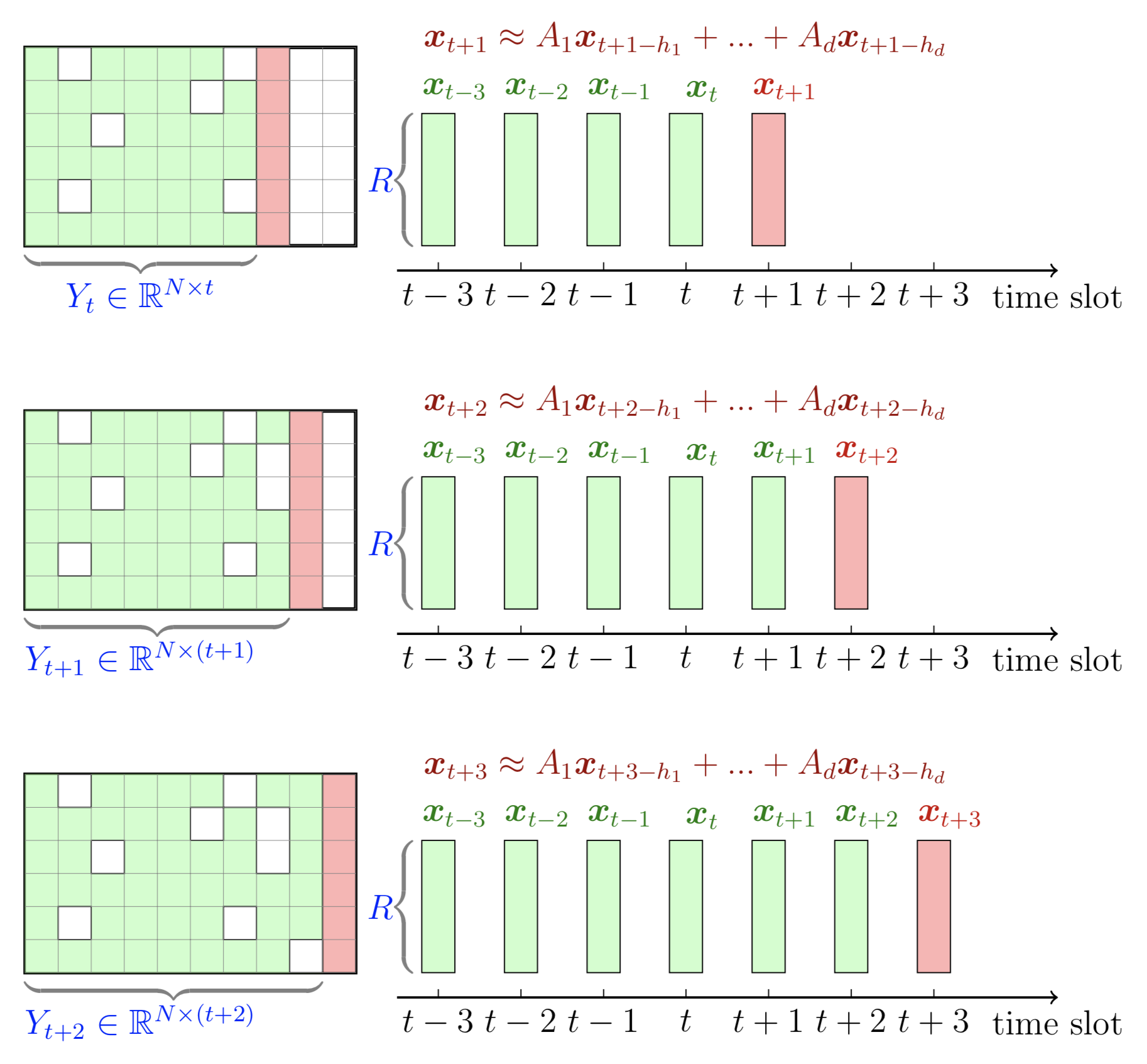

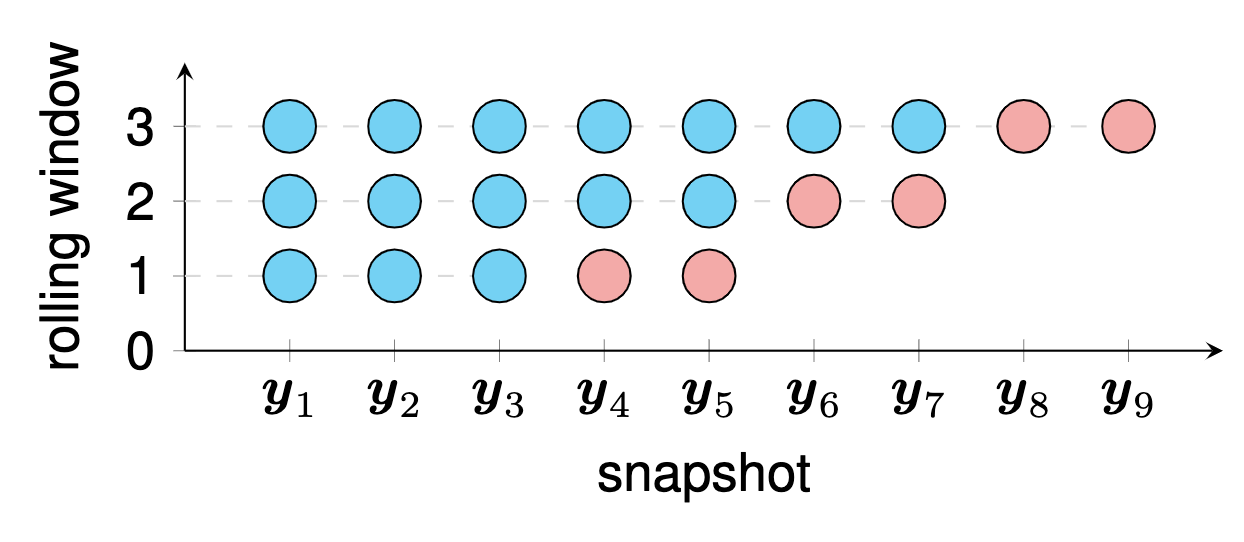
【例18】

この例では、時間行列因数分解を使用したローリング時系列予測をグラフで示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. drawとfilldraw使用してノードと四角形を設定します。

テンソル構造のtikz-3dplot

【例19】

この例では、3 次テンソルを図示します。この例を描画するには、次の手順に従います。

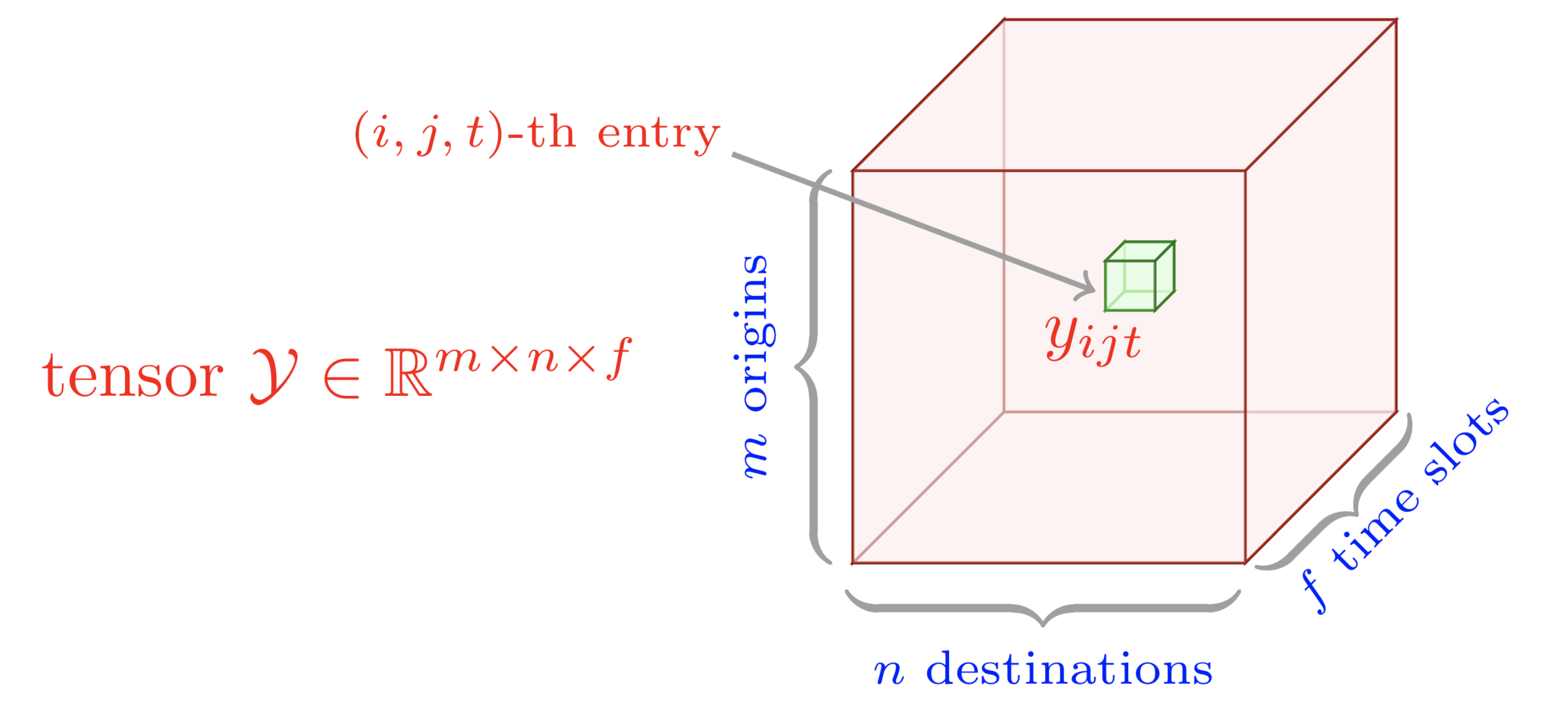
• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. テンソルエッジの座標を定義します。
  4. drawコマンドを使用してノードを定義します。

【例20】

この例では、3 次テンソルに対する古典的な CP テンソル因数分解を図示します。この例を描画するには、次の手順に従います。

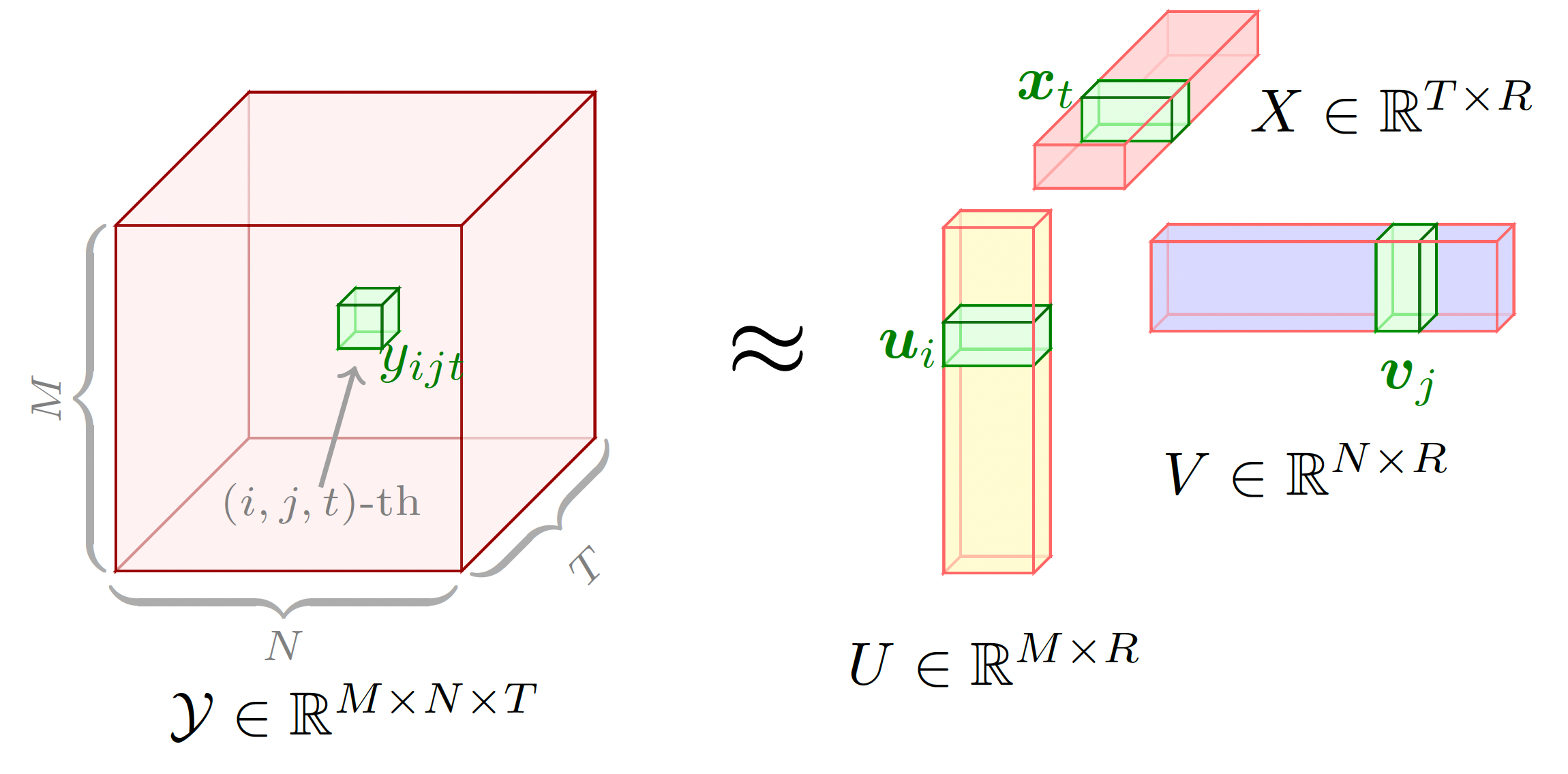
• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. テンソルエッジの座標を定義します。
  4. drawコマンドを使用してノードを定義します。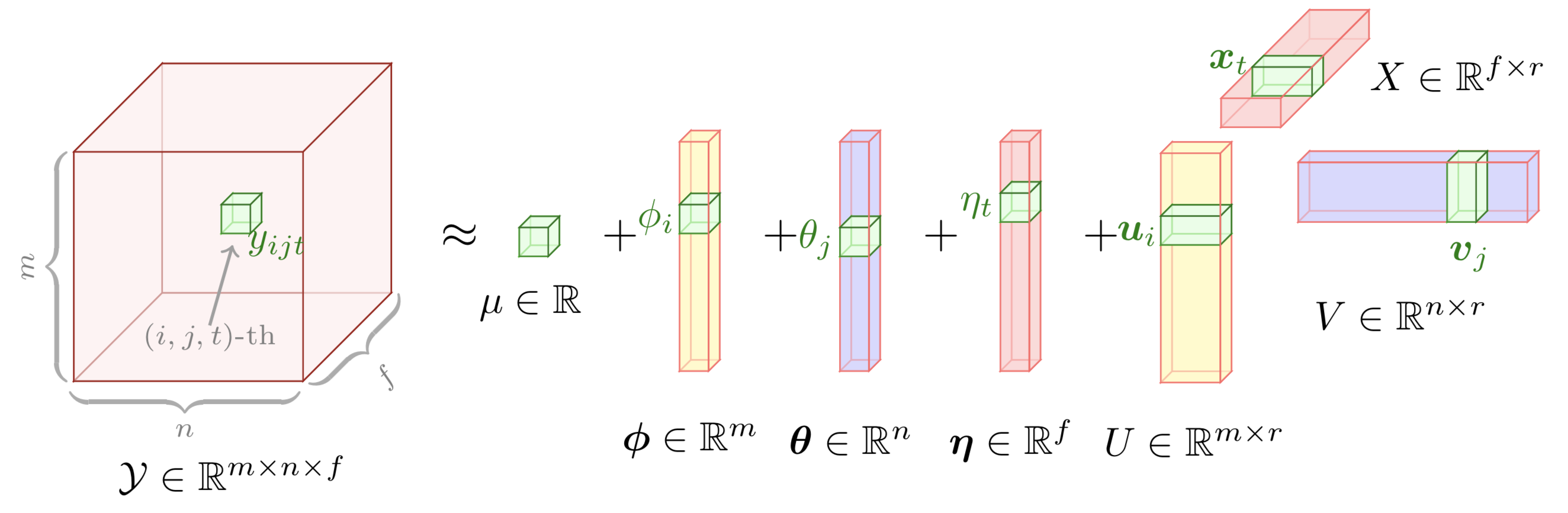

【例21】

この例では、拡張テンソル因数分解モデルをグラフィカルに示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. テンソルエッジの座標を定義します。
  4. drawコマンドを使用してノードを定義します。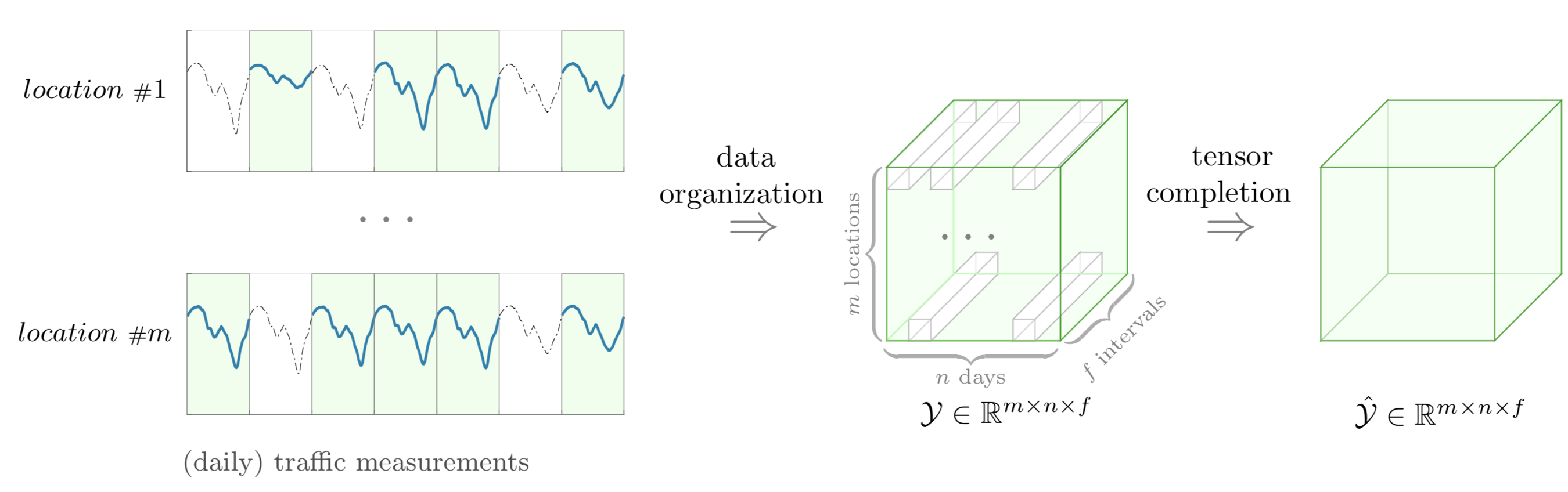

【例22】

この例では、トラフィック測定が部分的に観察される、データ編成とテンソル補完を含むテンソル補完タスクとそのフレームワークを図示します。この例を描画するには、次の手順に従います。

• リクエスト：
  1. 曲線1.pdfをアップロードし、
  2. 曲線2.pdfをアップロードします。
• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. テンソルエッジの座標を定義します。
  4. drawコマンドを使用してノードを定義します。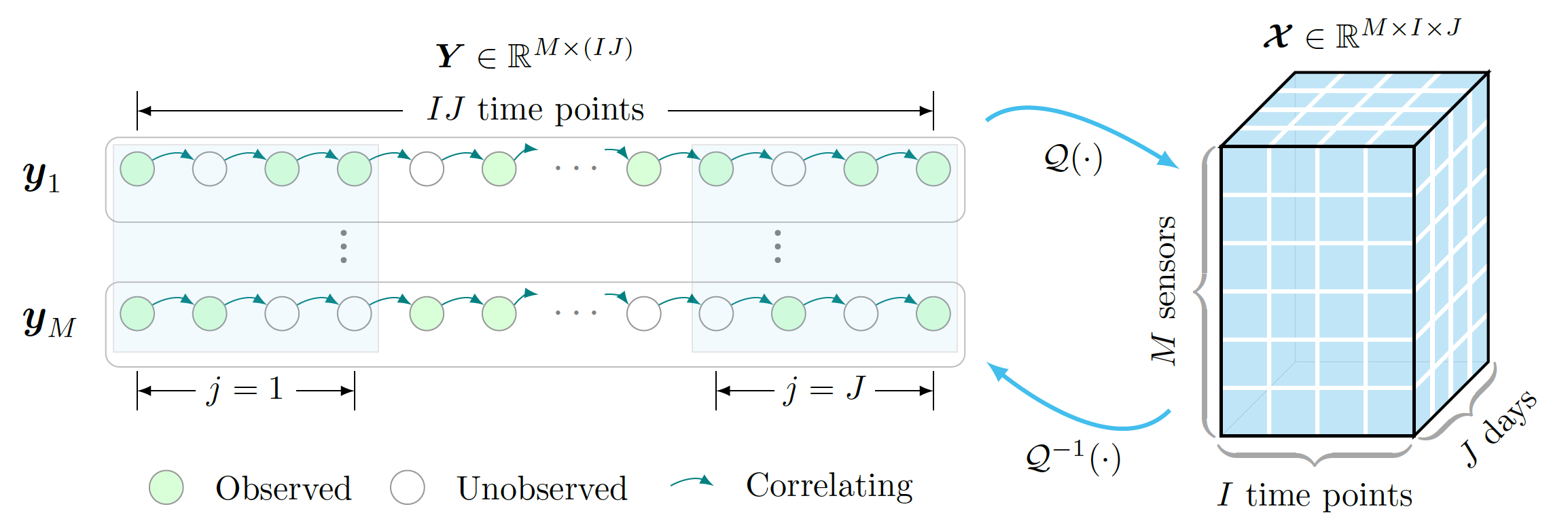

【例23】

この例では、低ランクの自己回帰テンソル補完モデルをグラフィカルに示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. node 、 path 、 plateコマンドを使用してノード、矢印、プレートを定義します。
  4. テンソルエッジの座標を定義します。
  5. drawコマンドを使用してノードを定義します。

【例24】

この例では、ユニタリ変換を使用したテンソル データの特異値しきい値処理の図を示します。この例を描画するには、次の手順に従います。

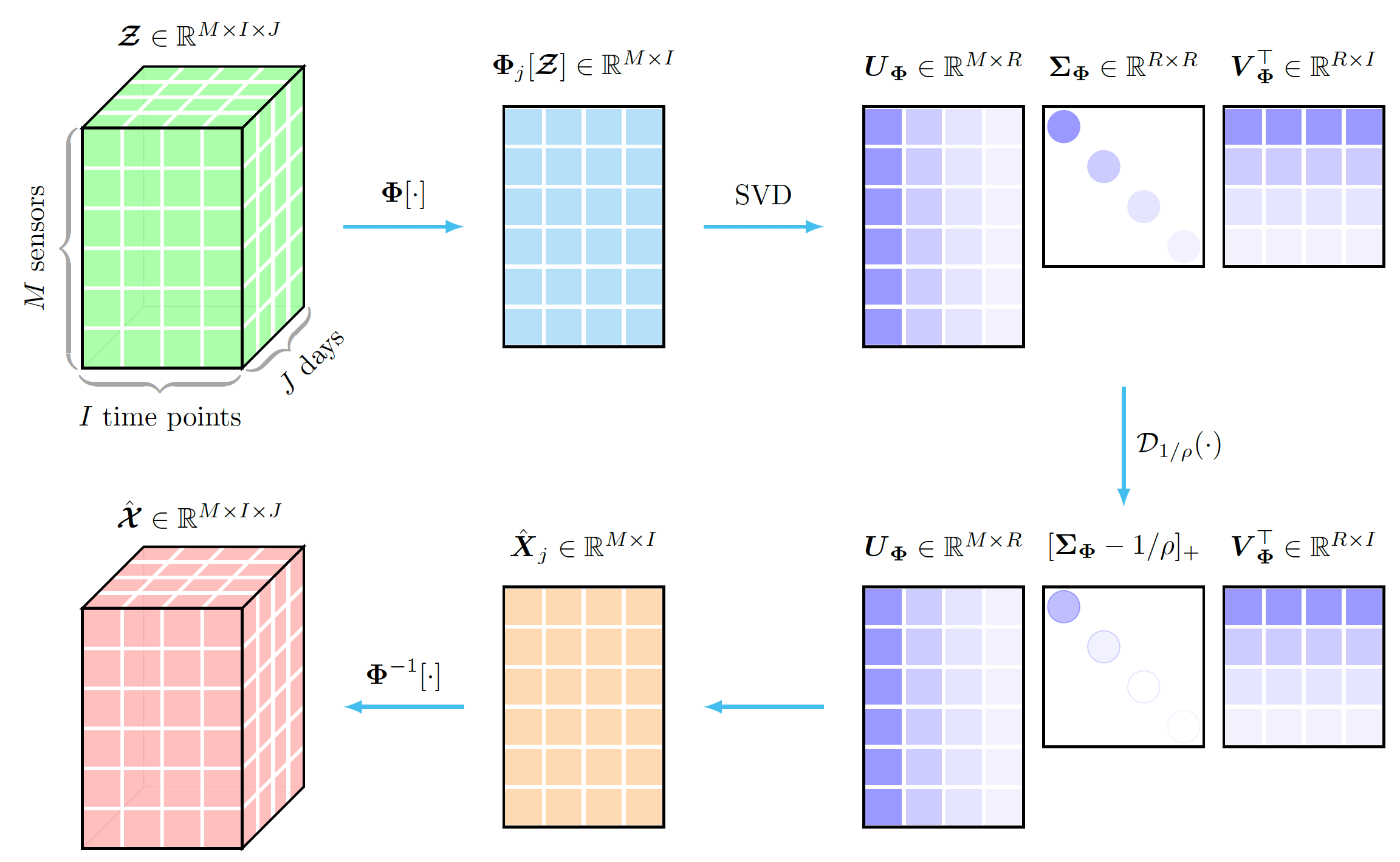
• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. nodeコマンドを使用してノードを定義します。
  4. テンソルエッジの座標を定義します。
  5. drawコマンドを使用してノードを定義します。
  6. filldrawコマンドを使用して四角形の色を定義します。

【例25】

この例では、低ランクのテンソル補完モデルをグラフィカルに示します。この例を描画するには、次の手順に従います。

• リクエスト：
  1. input_tensor.pdf をアップロードします。
  2. Output_tensor.pdf をアップロードします。
• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
  3. algorithm2eパッケージを使用します。
  4. usetikzlibrary{positioning, matrix, fit, calc}を使用します。
• bodyコード:
  1. begin{algorithm} end{algorithm}環境を使用してアルゴリズムを定義します。
  2. matrixコマンドを使用してコンポーネントを配置します。
  3. begin{scope} end{scope}を使用してレイヤーを含めます。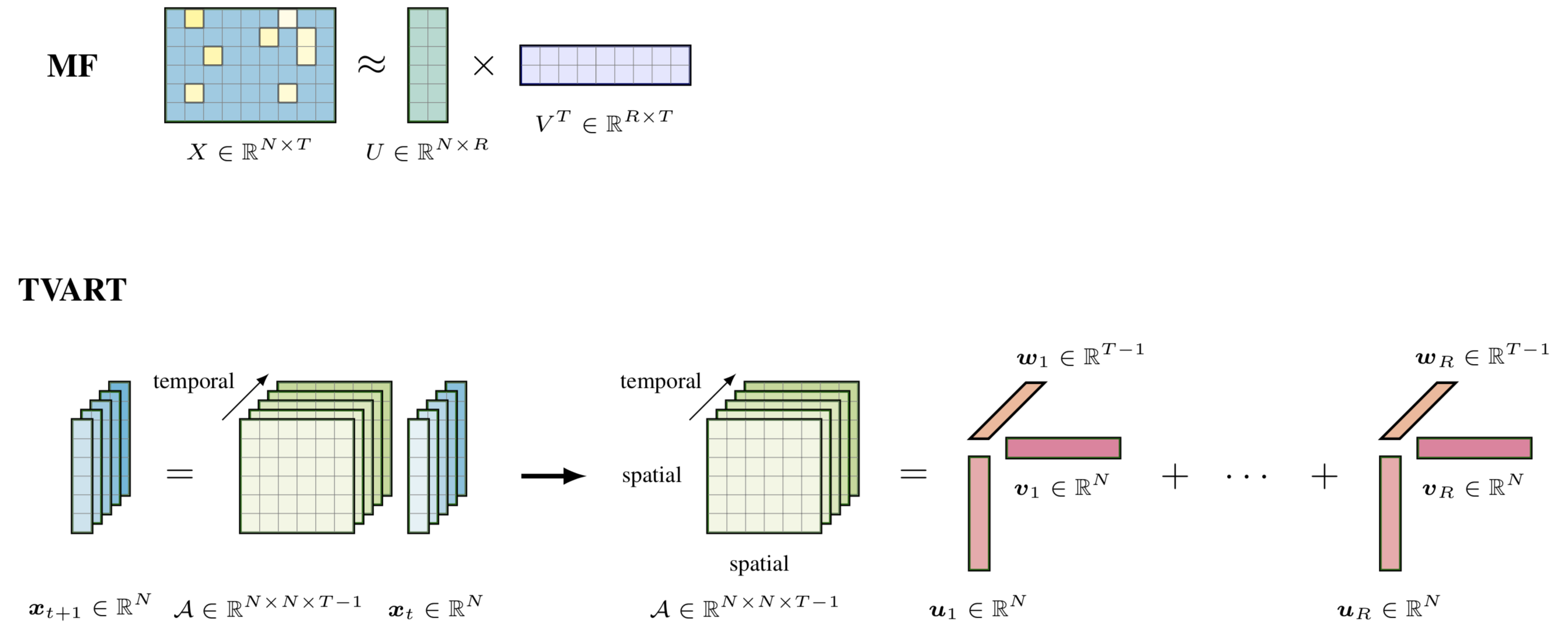

【例26】

この例では、低ランクのテンソル回帰モデルをグラフで示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. tikzとtikz-3dplotパッケージの両方を使用します。
• bodyコード:
  1. newcommand使用してDepth 、 Width 、およびHeightパラメータを設定します。
  2. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  3. drawコマンドを使用してノードを定義します。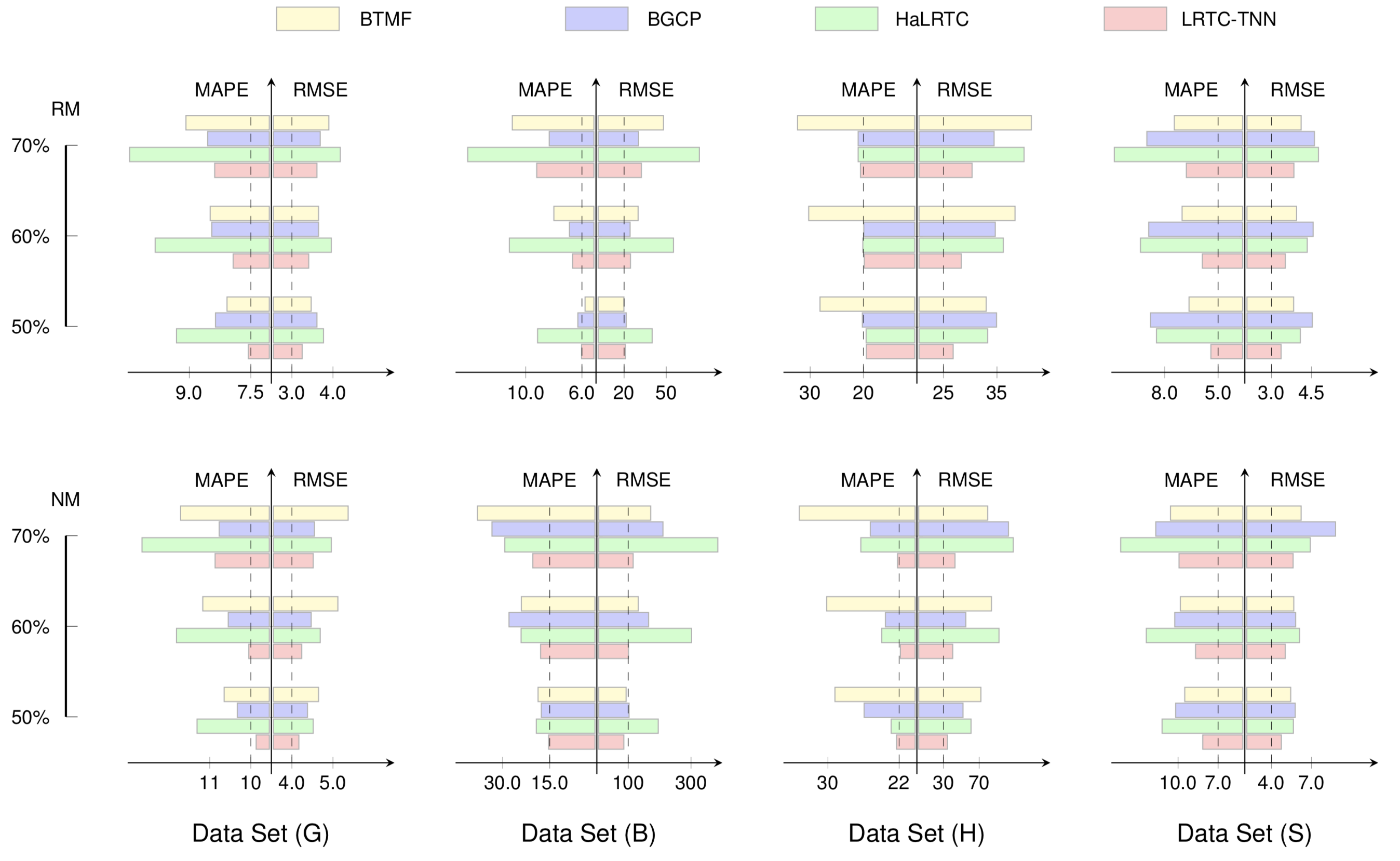

データの視覚化

【例27】

この例では、いくつかの行列モデルとテンソル モデルの代入精度を示します。この例を描画するには、次の手順に従います。

• preambleコード:
  1. documentclass standaloneとして定義し、
  2. パッケージtikzを使用します。
• bodyコード:
  1. begin{tikzpicture} end{tikzpicture}を使用して描画を開始します。
  2. drawコマンドを使用してノードを定義します。
  3. pgfuseimageコマンドを使用して画像をインポートします。

関連プロジェクト

• tikzベイズネット
• 素晴らしい-ティクズ
• トランスディム

出版物

これらの例のほとんどは、私たちの論文からのものです。

• Xinyu Chen、Zhanhong Cheng、HanQin Cai、Nicolas Saunier、Lijun Sun (2024)。交通時系列補完のラプラシアン畳み込み表現。知識およびデータ エンジニアリングに関する IEEE トランザクション、36 (11): 6490-6502。 [プレプリント] [DOI] [スライド] [データと Python コード]

• チェン・シンユー、スン・リージュン（2022）。多次元時系列予測のためのベイズ時間因数分解。パターン分析とマシン インテリジェンスに関する IEEE トランザクション、44 (9): 4659-4673。 [プレプリント] [DOI] [スライド] [データと Python コード]

• Xinyu Chen、Mengying Lei、Nicolas Saunier、Lijun Sun (2022)。時空間トラフィック データ代入のための低ランク自己回帰テンソル補完。高度道路交通システムに関する IEEE トランザクション、23 (8): 12301-12310。 [プレプリント] [DOI] [データと Python コード] (KDD 2021 の MiLeTS ワークショップにも一部受け入れられました。ワークショップ ペーパーを参照)

• チェン・シンユー、チェン・イーシアン、ニコラ・ソーニエ、スン・リージュン（2021）。時空間トラフィック データ代入のためのスケーラブルな低ランク テンソル学習。 Transportation Research Part C: Emerging Technologies、129: 103226. [プレプリント] [DOI] [データ] [Python コード]

• チェン・シンユー、スン・リージュン（2020）。多変量時系列予測のための低ランク自己回帰テンソル補完。 arXiv プレプリント arXiv: 2006.10436。 [プレプリント] [データと Python コード]

• チェン・シンユー、ヤン・ジンミン、スン・リージュン（2020）。時空間トラフィック データ補完のための非凸低ランク テンソル補完モデル。 Transportation Research Part C: Emerging Technologies、117: 102673. [プレプリント] [DOI] [データと Python コード]

• Xinyu Chen、Zhaocheng He、Yixian Chen、Yuhuan Lu、Jiawe Wang (2019)。ベイジアン拡張テンソル因数分解モデルを使用した、欠落しているトラフィック データの代入とパターンの検出。交通研究パート C: 新興技術、104: 66-77。 [DOI] [スライド] [データ] [Matlab コード] [Python コード]

• チェン・シンユー、何・ジャオチェン、スン・リージュン（2019）。時空間トラフィック データ代入のためのベイジアン テンソル分解アプローチ。交通研究パート C: 新興技術、98: 73-84。 [プレプリント] [DOI] [データ] [Matlab コード] [Python コード]