ai simplest network
1.0.0
これは、可能な限り最も単純な人工ニューラル ネットワークの説明と実証です。
人工ニューラル ネットワークは、相互接続された人工ニューロンがパターンを保存し、相互に通信することで脳からインスピレーションを受けています。最も単純な形式の人工ニューロンには 1 つまたは複数の入力があります
それぞれに特定の重さがある
そして1つの出力
。
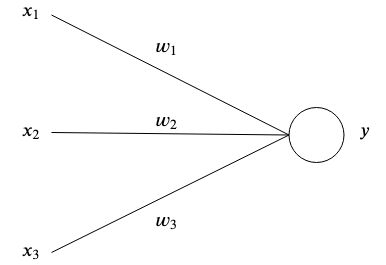
最も単純なレベルでは、出力は入力と重みの合計です。
ネットワークの目的は、特定の出力を学習することです特定の入力が与えられた場合
多くのパラメータを持つ複雑な関数を近似することによって
自分たちでは思いつかなかったということ。
2 つの入力を持つネットワークがあるとします。 
そして
そして2つの重り
そして
。
考え方は、指定された入力が目的の出力を生成するように重みを調整することです。
事前に最適な値を知ることができないため、重みは通常ランダムに初期化されますが、簡単にするために両方を次のように初期化します。 
。
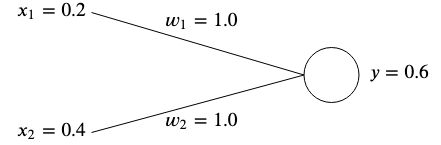
このネットワークの出力を計算すると、次のようになります。
出力の場合予想されるターゲット値と一致しない場合は、エラーが発生します。
たとえば、次の目標値を取得したい場合、 
そうすれば、次のような違いが生じます。
誤差 (コスト関数とも呼ばれる) を測定する一般的な方法の 1 つは、平均二乗誤差を使用することです。
入力とターゲット値の関連付けが複数ある場合、誤差は各関連付けの平均合計になります。
平均二乗誤差を使用して、結果が目的のターゲットからどれだけ離れているかを測定します。二乗により負の符号が除去され、出力とターゲットの間のより大きな差がより重視されます。
エラーを修正するには、出力がターゲットと一致するように重みを調整する必要があります。この例では、 から
に
うまくいくでしょう、なぜなら
ただし、多くの異なる入力やターゲット値に対してニューラル ネットワークの重みを調整するには、これを自動的に行う学習アルゴリズムが必要です。
考え方は、誤差を使用して、誤差を最小限に抑えるために各重みをどのように調整する必要があるかを理解することですが、まず勾配について学ぶ必要があります。
これは本質的に、関数の最急上昇の方向を指すベクトルです。勾配は で表されます。 
これは、ベクトルとして表現された関数の各変数の偏導関数にすぎません。
2 変数関数の場合は次のようになります。
いくつかの数値を注入し、簡単な例で勾配を計算してみましょう。関数があるとしましょう
の場合、勾配は次のようになります。
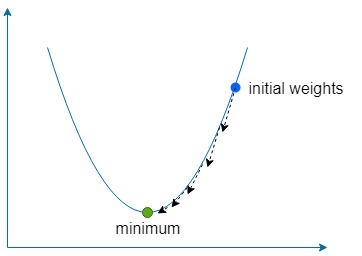
下降部分は単に、勾配を使用して関数の最も急な上昇の方向を見つけ、次に少量ずつ反対方向に何度も進み、関数のグローバル (またはローカル) 最小値を見つけることを意味します。
学習率と呼ばれる定数を使用します。 
その方向に向かってどれだけ小さな一歩を踏み出すかを定義します。
もしが大きすぎると、関数の最小値をオーバーシュートする危険性がありますが、小さすぎると、ネットワークの学習に時間がかかり、浅い極小値に陥る危険性があります。
2 つの重みについてそして誤差関数に関するこれらの重みの勾配を見つける必要があります。 
どちらにとってもそして 、連鎖則を使用して勾配を見つけることができます。
これからは、 
として
単純さを表す言葉。
勾配を取得したら、計算された勾配と学習率の積を減算して重みを更新できます。
そして、誤差が最小限に抑えられ、ゼロに十分近づくまでこのプロセスを繰り返します。
含まれている例では、勾配降下法を使用して、2 つの入力と 1 つの出力を持つニューラル ネットワークに次のデータセットを教えます。
一度学習すると、ネットワークは 2 つ与えられたときに ~0 を出力するはずです。 と〜 与えられたときそして
。
docker build -t simplest-network .
docker run --rm simplest-network
