三目並べ (または三目並べ) ゲームにおける Minimax AI アルゴリズムの実装。試してみましょう: 三目並べ - ミニマックス
AI を使用してゲームを解決するために、ミニマックス アルゴリズムに従うゲーム ツリーの概念を導入します。ゲームのさまざまな状態は、ゲーム ツリー内のノードによって表され、上記の計画問題と非常によく似ています。考え方が少し違うだけです。ゲーム ツリーでは、ツリーの「ルート」ノード (通常は図の上部に表示されます) がゲームの開始位置となるように、ノードはゲームでの各プレイヤーのターンに対応するレベルに配置されます。三目並べでは、これはまだ X も O もプレイされていない空のグリッドになります。第 2 レベルのルートの下には、X または O など、最初のプレイヤーの動きから生じる可能性のある状態があります。これらのノードをルート ノードの「子」と呼びます。
第 2 レベルの各ノードはさらに、その子ノードとして、相手プレイヤーの動きによってそこから到達できる状態を持ちます。これは、ゲームが終了する状態に達するまで、レベルごとに続けられます。三目並べでは、どちらかのプレイヤーが 3 列を揃えて勝つか、ボードがいっぱいになってゲームが引き分けで終了することを意味します。
Minimax は、三目並べ、チェッカー、チェス、囲碁などの 2 人用ゲームに適用される人工知能です。このゲームはゼロサム ゲームとして知られています。数学的に表現すると、1 人のプレイヤーが勝ち (+1)、もう 1 人のプレイヤーが負け (-1)、または両方とも勝てなかった (0) からです。
アルゴリズムは、 Maxプレーヤーが勝つか負けない (引き分け) につながる最善の手を再帰的に検索します。ゲームの現在の状態とその状態で利用可能な手を考慮し、最終状態 (勝ち、引き分け、負け) が見つかるまで、有効な手ごとに ( minとmax を交互に) プレイします。
このアルゴリズムは、書籍『Algorithms in a Nutshell』 (George Heineman、Gary Pollice、Stanley Selkow、2009 年) で研究されました。疑似コード (適応):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
ここで、Python 実装を使用したこの疑似コードの各部分を見ていきます。 Python 実装はこのリポジトリで入手できます。まず第一に、次のことを考慮してください。
ボード = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
最大 = +1
最小 = -1
MAX は X または O であり、MIN は O または X のいずれでも構いません。ボードは3x3です。
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]両プレイヤーともあなたの最悪のスコアからスタートします。プレイヤーがMAXの場合、スコアは-無限大です。それ以外の場合、プレイヤーが MIN の場合、スコアは +infinity になります。注: infinity は、inf (Python の math モジュールから) のエイリアスです。
ボード上での最善の手は、すべて [-1, -1] (行と列) です。
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return score深さがゼロに等しい場合、ボードにはプレイできる新しい空のセルがありません。または、プレイヤーが勝った場合、MAX または MIN でゲームが終了したことになります。したがって、その州のスコアが返されます。
ここで、再帰を含むこのコードの主要部分を見てみましょう。
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y有効な各移動 (空のセル) について:
盤面上の移動(+1または-1)を元に戻し、行、列を回収します。
次のステップは、スコアを最高のものと比較することです。
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreMAXプレイヤーの場合、より大きなスコアが得られます。 MIN プレーヤーの場合は、より低いスコアが与えられます。そして最後には最善手が返される。最終的なアルゴリズム:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best 以下では、最大値が左側の 2 番目のノードにあるため、最適な手は中央にあります。
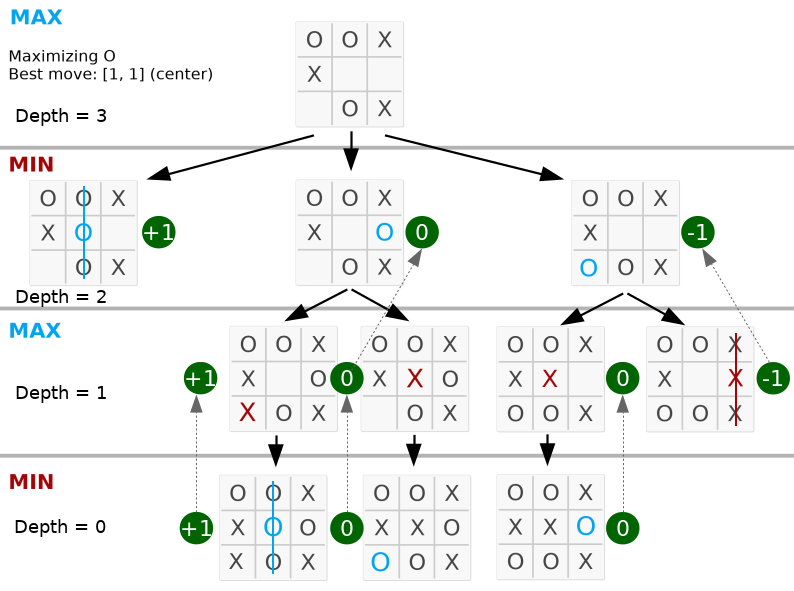
深さがボード上の有効な動きと等しいことを確認してください。完全なコードはpy_version/で入手できます。
簡略化されたゲームツリー:
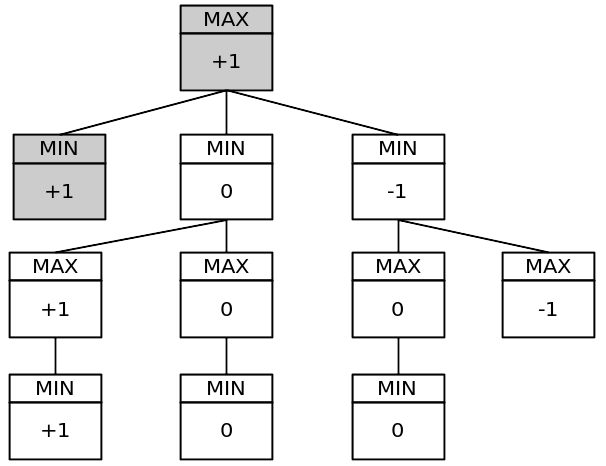
そのツリーには 11 個のノードがあります。完全なゲーム ツリーには 549.946 ノードがあります。静的グローバル変数をプログラムに配置し、ターンごとのミニマックス関数呼び出しごとにそれをインクリメントすることでテストできます。
チェスのようなより複雑なゲームでは、ゲーム ツリー全体を検索するのは困難です。ただし、アルファ ベータ プルーニングはミニマックス アルゴリズムの最適化手法であり、検索で無関係なノード (サブツリー) を切り取るため、検索ツリー内の一部の分岐を無視できるようになります。詳細については、以下を参照してください。