このプロジェクトはブースト(数学/差別化/自動装置)に移行し、このリポジトリは更新されなくなりました。
| 支店 | トラビス | Appveyor | codecov.io |
|---|---|---|---|
master | |||
develop |
AutoDiffは、単一変数と複数の変数の数学機能の自動分化(フォワードモード)を容易にするヘッダーのみのC ++ライブラリです。
この実装は、ポイントx₀での分析関数fのテイラーシリーズの拡張に基づいています。
自己Diffの本質的な考え方は、 F(x₀)の評価において、多項式を持つ数値を置き換えることです。数値x₀を一次多項式x₀+εに置き換え、同じアルゴリズムを使用してf(x₀+ε)を計算することにより、 εの結果の多項式には関数の誘導体f '(x₀) 、 f' '(x₀)が含まれます。 、 f '' '(x₀) 、...係数内。各係数は、それぞれの順序の導関数に等しく、順序の要因で割ったものです。
より詳細には、 x₀でfの最初のn誘導体を計算することに関心があると仮定します。導関数の計算の精度を失うことなく、 nより大きいεのパワーを含むすべての項o( εn+1 )を破棄できます。 (これは、多項式の各用語は、算術操作の下で等しい項と低次の項にのみ依存するという事実によるものです。)これらの切り捨て規則の下で、 Fは多項式から脳腫瘍への変換を提供します。
C ++のオペレーターと関数を過負荷にする能力により、 εの多項式を表すクラスfvarの作成が可能になります。したがって、一般的な(テンプレート)タイプの受容変数と戻り変数に書き込まれた場合、 y₀= f(x₀)の数値を計算する同じアルゴリズムfは、多項式ʃn ynεⁿ = f(x₀++ ε) 。次に、誘導体F (n) (x₀)は、それぞれの要因Nの積から見られます!および係数y n :

#include <boost/math/difteriation/autodiff.hpp> #include <iostream> template <typename t>
t fourth_power(t const&x){
t x4 = x * x; // operator*()のretvalは、NRVOを介してx4のメモリを使用します。
x4 *= x4; //正方形の場合でもX4のコピーはoperator*=()内に作成されていません。
x4を返します。 // x4は、nrvo。} int main()を介してmain()でyのメモリを使用します。
constexpr unsigned Order = 5; //計算される最高のデリバティブ。
auto const x = make_fvar <double、order>(2.0); // x = 2で誘導体を見つけます。
自動const y = fourth_power(x); for(unsigned i = 0; i <= order; ++ i)
std :: cout << "y.derivative(" << i << ")=" << y.derivative(i)<< std :: endl; 0を返します。
}/*output:y.derivative(0)= 16y.derivative(1)= 32y.derivative(2)= 48y.derivative(3)= 48y.derivative(4)= 24y.derivative(5)= 0*/上記の計算
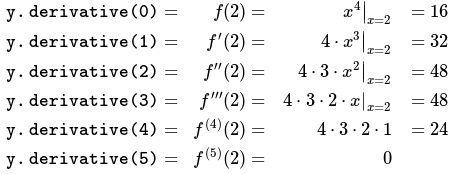
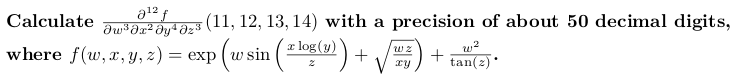
#include <boost/math/difteriation/autodiff.hpp> #include <boost/multiprecision/cpp_bin_float.hpp> #include <iostream> namespace boost :: math :: template <typename w、typename x、typename y、typename y、 TypeName Z>
<w、x、y、z> f(const w&w、const x&x、const y&y、const z&z){namespace std;
return exp(w * sin(x * log(y) / z) + sqrt(w * z /(x * y)) + w * w / tan(z);
} int main(){float50 = boost :: multiprecision :: cpp_bin_float_50;の使用 constexpr unsigned nw = 3; // wを計算するデリバティブの最大順序
constexpr unsigned nx = 2; // xを計算するデリバティブの最大順序
constexpr unsigned ny = 4; // yを計算するデリバティブの最大順序
constexpr unsigned nz = 3; // zを計算するデリバティブの最大順序
// 4個の独立変数をSTD :: Tupleに宣言します。
Auto const変数= make_ftuple <float50、nw、nx、ny、nz>(11、12、13、14); auto const&w = std :: get <0>(変数); // w = 11のnwデリバティブまで
auto const&x = std :: get <1>(変数); // x = 12でnx誘導体まで
auto const&y = std :: get <2>(変数); // y = 13でNY誘導体まで
auto const&z = std :: get <3>(変数); // z = 14のNZ誘導体まで
Auto const v = f(w、x、y、z); // Mathematicaのシンボリック差別化から計算。
Float50 const Answer( "1976.3196007477977177779881875290418720908121189218755");
std :: cout << std :: setprecision(std :: numeric_limits <float50> :: digits10)
<< "Mathematica:" << Answer << 'n' << "autodiff:" << v.derivative(nw、nx、ny、nz)<< 'n' << std :: setprecision(3)
<< "相対エラー:" <<(v.derivative(nw、nx、ny、nz) / answer -1)<< 'n'; 0を返します。
}/*Output:mathematica : 1976.3196007477977177798818752904187209081211892188autodiff : 1976.3196007477977177798818752904187209081211892188relative error: 2.67e-50*/#include <boost/math/didimatiut/autodiff.hpp> #include <iosteam> namespace boost :: math :: constants; namespace boost :: math :: dishipiation; //方程式と機能/変数名は//から// https://en.wikipedia.org/wiki/greeks_(finance)#formulas_for_european_option_greeks//
x phi(x const&x){return 0.5 * erfc(-one_div_root_two <x>() * x);
} enum class cp {call、put}; //年間配当利回りをゼロ(q = 0).template <typename spric、typename sigma、typename tau、typeNameレート>
宣伝<プライス、シグマ、タウ、レート> black_scholes_option_price(cp cp、double k、
価格const&s、
Sigma Const&Sigma、
タウconst&tau、
const&r){namespace stdを使用しています。
Auto const d1 =(log(s / k) +(r + sigma * sigma / 2) * tau) /(sigma * sqrt(tau)); Auto const d2 =(log(s / k) +(r -sigma * sigma / 2) * tau) /(sigma * sqrt(tau)); switch(cp){case cp :: call:return s * phi(d1) - exp(-r * tau) * k * phi(d2); case cp :: put:return exp(-r * tau) * k * phi(-d2)-s * phi(-d1);
}
} int main(){double const k = 100.0; //行使価格。
auto const s = make_fvar <double、2>(105); //株価。
double const sigma = 5; //ボラティリティ。
double const tau = 30.0 / 365; //長年にわたって有効期限までの時間。 (30日)。
double const r = 1.25 / 100; // 金利。
auto const call_price = black_scholes_option_price(cp :: call、k、s、sigma、tau、r); Auto const put_price = black_scholes_option_price(cp :: put、k、s、sigma、tau、r);
std :: cout << "black-scholes call price =" << call_price.derivative(0)<< 'n' << "black-scholes put =" << put_price.derivative(0)<< 'n' << "call delta =" << call_price.derivative(1)<< 'n' << "put delta =" << put_price.derivative(1)<< 'n' << "call gamma =" << call_price .derivative(2)<< 'n' << "put gamma =" << put_price.derivative(2)<< 'n'; 0を返します。
}/*output:ブラックスコールコール価格= 56.5136BLACK-SCHOLES PUT PROT = 51.4109CALL DELTA = 0.773818PUT DELTA = -0.226182CALL GAMMA = 0.00199852put Gamma = 0.00199852*//自動化されたオプションギリシャ人のより大きなリストについては、example/black_scholes.cppを参照してください。
上記の例は、AutoDiffを使用することの利点のいくつかを示しています。
コード冗長性の排除。 n誘導体を計算するためのn個の関数の存在は、コード冗長性の形式であり、それに伴うすべての負債があります。
1つの関数の変更には、他の関数に追加の変更が必要です。上記の3番目の例では、ギリシャの価値ごとに別の関数が書かれている場合、上記のコードベースがどれだけ大きく依存しているかを検討してください。
異なる目的の微分関数への依存性は、元の関数に変更が加えられたときに破損します。存在する必要がないものは壊れることはできません。
コード肥大化、概念的完全性の低下。コードベースが小さく、直感的に把握できる場合、コードの進化の制御はより簡単/安全です。
有限差分法よりも誘導体の精度。シングルリテレーション有限差分方法には、常にアプリケーションごとに慎重に選択する必要があるΔXフリー変数が含まれています。 Δxが小さすぎると、数値エラーが大きくなります。 Δxが大きすぎると、数学的エラーが大きくなります。 AutoDiffでは、設定する自由変数はありません。ΔXの最良の選択であっても、回答の精度は一般に有限差分法よりも優れています。
追加の詳細は、AutoDiffマニュアルにあります。
Boost Softwareライセンスバージョン1.0の下で配布されます。
ヘッダーのみ。
C ++ 17向けに最適化されています。また、C ++ 11、C ++ 14を編集してテストし、C ++ 20標準を提案しました。
すべてのメモリはスタックに割り当てられます。
| 名前 | 目的 |
|---|---|
doc | ドキュメント |
example | 例 |
include | ヘッダー |
test | ユニットテスト |
バグをレポート:使用しているブーストバージョン、プラットフォーム、コンパイラにお問い合わせください。問題を再現するための小さなまとめ可能なコードサンプルも常に良いです。
開発ブランチに対するプル要求としてパッチを提出します。パッチを送信することにより、Boost Softwareライセンスバージョン1.0に基づく変更のライセンスに同意することに注意してください。