40 年間続いたコンピュータ サイエンスの問題であるビジー ビーバー問題が、アマチュアのグループによってついに解決されました。この画期的な開発は学術界に衝撃を与えただけでなく、有名な数学者テレンス・タオによっても認められ、1983 年以来この分野で最も重要な開発として賞賛されました。 Coq 証明アシスタントを使用して、彼らは 5 番目のビジー ビーバー番号 BB(5) の値が 47,176,870 であることを検証することに成功しました。これは、複雑な数学的問題を解決する際のソフトウェア支援証明の大きな可能性を実証するとともに、チューリング マシンの動作に関する洞察も提供します。そして新たな問題の解決。
コンピューター サイエンスの神秘的な分野で、ビジー ビーバー問題と呼ばれる 40 年前の問題が最近、アマチュアのグループによって解決されました。この成果は学術界にセンセーションを巻き起こしただけでなく、有名な数学者テレンス・タオによっても認められ、ソーシャルメディアでこのニュースを転送し、数学研究における証明助手の重要性を強調した。
コンピューター科学者のスコット・アーロンソンもこの発見を高く評価し、これは 1983 年以来の多忙なビーバー機能研究における最も重要な発展であると信じています。この成果は、計算理論の境界に対する深い理解を示すものであり、複雑な数学的問題を解決する際のソフトウェア支援証明の可能性を実証しています。
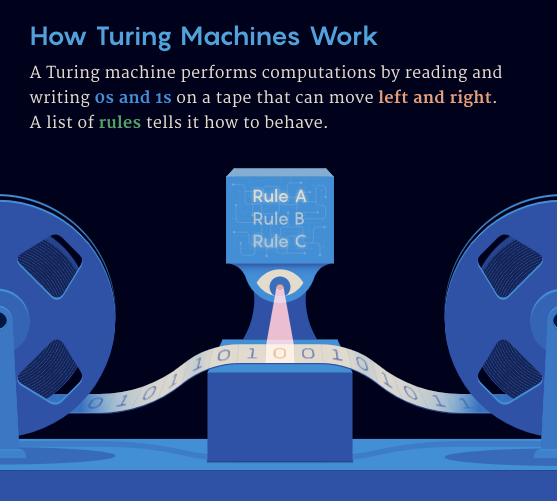
ビジー ビーバー問題は、40 年以上前にドイツのドルトムントでコンピュータ科学者たちが、停止する前に最も多くの 1 を書き込むことができる特定のチューリング マシンを見つけようとしたときに始まりました。チューリング マシンは、1936 年にアラン チューリングによって提案された抽象的なコンピューティング モデルで、無限に長い磁気テープ上で 0 と 1 を読み書きすることで計算を実行します。

1974 年に 4 番目の忙しいビーバーの番号が決定された後、5 番目のビーバーを見つけることは未解決の問題になりました。現在、世界中の 20 人以上の寄稿者が参加するオンライン コミュニティが、Coq と呼ばれる証明アシスタント ソフトウェアを使用して、5 番目の Busy Beaver 番号 BB(5) の値が 47,176,870 であることを検証することに成功しました。
この成果はコミュニティを興奮させただけでなく、コンピューター科学者のダミアン・ウッズも驚きを呼び起こし、その進歩をウサイン・ボルトのスピードに例えました。この問題の解決策はコンピューター サイエンスの他の分野に直接適用できるわけではありませんが、参加者にとって、数学的不可能性との闘いそれ自体が最大の報酬です。
ビジー ビーバー問題の核心は、チューリング マシンの動作、特に問題を停止する際のパフォーマンスを理解することにあります。チューリング マシンの動作は、テーブルとして想像できる一連のルールによって定義されます。各ルールは、読み取り/書き込みヘッドが特定の状態で 0 または 1 に遭遇したときに実行する必要があるアクションを指定します。
チューリング マシンは無限ループに陥る可能性がありますが、チューリング マシンが実行を停止するかどうかを判断することは、未解決の問題として知られています。数学者のティボール・ラドーはこの結論に満足できず、ルールの数に従ってチューリングマシンをグループ化し、停止問題の性質を探る「忙しいビーバーゲーム」を発明しました。
アレン・ブレイディなどの初期の研究者は、チューリング マシンの動作をシミュレートするプログラムを作成することでこの問題を調査しました。彼の研究と他の研究者の発見は、後の探検家の基礎を築きました。
2022 年まで、大学院生のトリスタン ステリンは、BB(5) の完成を目的としたオンライン共同プロジェクトである Busy Beaver Challenge を立ち上げました。革新的な方法と Coq 証明アシスタントの助けにより、チームはついに 5 匹目の忙しいビーバーを見つけることに成功しました。
この成果は、数学の不可能性への挑戦であるだけでなく、コンピューター サイエンスの限界の探求でもあります。 BB(5) が確認されたため、研究者らは Coq 証明を補完する人間が読めるバージョンとなる学術論文の草稿を作成しています。同時に、BB(6)の探査が次の目標となるかどうかについても検討している。
参考: https://www.quantamagazine.org/amateur-mathematicians-find-fifth-busy-beaver-turing-machine-20240702/
ビジー ビーバー問題の解決策は、数学の分野における大きな進歩であるだけでなく、将来のコンピューティング理論研究に新しい方向性とアイデアを提供します。 この成果により、より多くの人々が数学やコンピューター サイエンスの研究に参加し、未知の領域を一緒に探索することが奨励されます。