Lanczos(Lanchos로 발음) 리샘플링은 디지털 신호를 보간하기 위한 정교한 기술로, 최근접 이웃 및 쌍선형 보간과 같은 간단한 방법에 비해 우수한 이미지 품질을 제공합니다. 세부 사항을 효과적으로 보존하고 앨리어싱 아티팩트를 최소화함으로써 Lanczos 리샘플링은 이미지 및 신호 처리 응용 프로그램에 널리 사용됩니다.
Lanczos는 이미지 품질이 뛰어나지만 계산 복잡성이 증가하는 대가를 치르게 됩니다. 또한 특히 날카로운 모서리 주변에 "링잉" 아티팩트가 발생할 가능성이 단점이 될 수 있습니다. 이러한 과제에도 불구하고 Lanczos는 전반적인 성능 이점으로 인해 이미지 크기 조정 및 회전과 같은 작업에 여전히 선호되는 선택입니다.
이 문서는 이론적 토대, 구현 세부 사항 및 실제 적용을 포함하여 Lanczos 리샘플링에 대한 포괄적인 개요를 제공합니다. 이 강력한 기술을 이해하고 활용하려는 개발자와 연구자에게 귀중한 리소스 역할을 합니다. 후속 섹션에서는 Lanczos 커널, 보간 및 리샘플링 프로세스, 플럭스 보존, 업샘플링, 다운샘플링, 샘플 위치 지정, 출력 범위, 다차원 보간 및 분리 가능성과 같은 Lanczos 리샘플링의 중요한 측면을 탐구합니다. 소스 코드와 함께 실제 예제가 포함되어 있습니다.
주어진 지원 크기에 대해 정의된 Lanczos 커널은 Lanczos 리샘플링에 사용되는 함수입니다. 커널은 다음과 같이 정의됩니다.
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
어디:
정규화된 sinc 함수는 다음과 같이 정의됩니다.
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
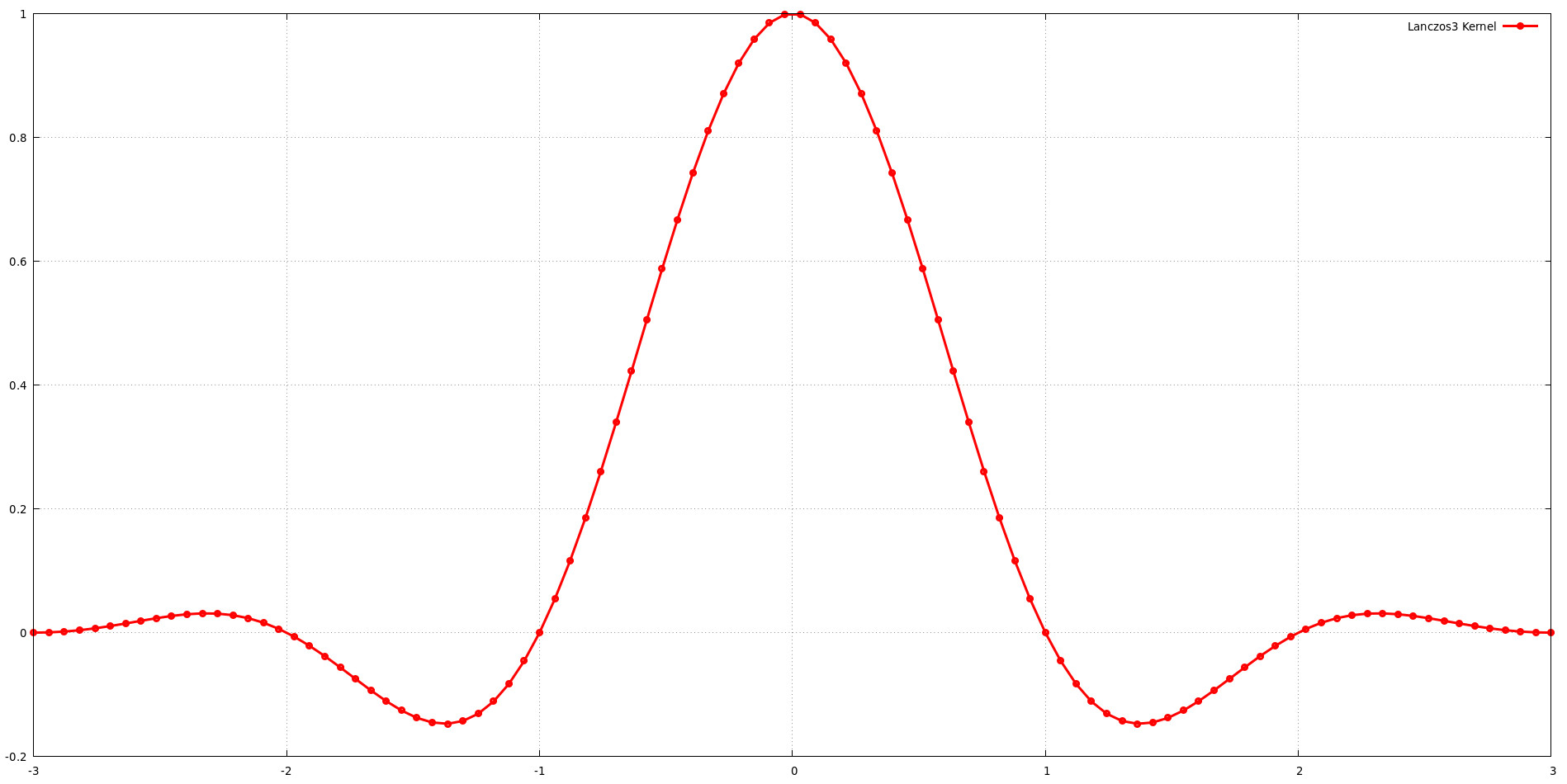
그래프는 a = 3의 지원 크기에 대한 Lanczos 커널의 모양을 보여줍니다. 이는 커널에 sinc 함수의 3개 로브가 포함되어 있음을 의미합니다. 지원 크기(a)를 늘리면 일반적으로 주파수 응답을 형성하는 데 더 많은 유연성이 제공되지만 계산 비용도 증가합니다. 지원 크기를 선택할 때 이미지 품질과 계산 효율성 사이의 균형을 맞춰야 합니다. a = 3인 Lanczos 커널이 저주파 보존과 고주파 제거의 탁월한 균형을 제공한다는 Jim Blinn의 발견은 이러한 개념을 뒷받침합니다.
참고: "커널 너비", "지원 크기" 및 "필터 크기"라는 용어는 매개변수 a를 설명하기 위해 종종 같은 의미로 사용됩니다. 그러나 Lanczos 리샘플링의 맥락에서는 "지원 크기"가 개념을 가장 정확하게 반영합니다.
Lanczos 보간은 이산 신호를 새로운 샘플링 속도로 리샘플링하는 데 사용되는 기술입니다. Lanczos 커널로 원래 신호를 컨볼루션하여 이를 달성합니다.
보간된 신호 s2(x)는 다음과 같이 계산할 수 있습니다.
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
어디:
플럭스 보존:
정규화 계수 w(x)는 보간 프로세스 중에 전체 신호 에너지 또는 질량을 보존하는 데 중요합니다. 이는 보간된 값의 합이 원본 샘플의 합과 비슷하도록 보장합니다. 필터 중량은 다음과 같이 계산됩니다.
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
업샘플링:
샘플링 속도를 높일 때 Lanczos 보간 방정식을 수정 없이 바로 사용할 수 있습니다.
다운샘플링:
샘플링 속도를 줄일 때 앨리어싱 아티팩트를 방지하려면 필터 스케일을 새 샘플링 속도와 일치하도록 조정해야 합니다.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
어디:
n1 샘플에서 n2 샘플로 신호를 리샘플링할 때 다음 샘플 위치가 사용됩니다. 인덱스 j는 샘플링된 신호 s2(x)의 샘플을 나타내는 데 사용됩니다. (j + 0.5) 항은 s2(x)에 있는 표본의 중심입니다. 이 단계에서는 s2(x)의 점을 s1(x)의 점으로 조정합니다. x의 마지막 -0.5 항은 Lanczos 계수 샘플이 오프셋되도록 하는 위상 변이입니다.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
Lanczos 보간을 수행할 때는 신호 경계에 특별한 주의를 기울여야 합니다. 일반적인 가장자리 처리 기술은 다음과 같습니다.
제로 패딩:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
클램핑:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
클램핑은 가장자리 근처의 날카로운 불연속성으로 인해 발생하는 가장자리 아티팩트를 줄이기 때문에 선호되는 경우가 많습니다. 그러나 가장자리 처리 방법의 선택은 특정 응용 프로그램과 원하는 출력에 따라 달라집니다.
s2(x)의 범위는 L(x)의 로브로 인해 s1(x)의 범위보다 클 수 있습니다. 예를 들어, [0.0,1.0] 범위의 픽셀 색상에 해당하는 입력 신호 s1(x)는 부호 없는 바이트 [0,255]로 다시 변환할 때 출력 값이 오버플로되지 않도록 동일한 범위로 고정되어야 합니다. .
Lanczos 커널은 다차원으로 확장되어 이미지나 고차원 데이터에 대한 보간을 수행할 수 있습니다.
2차원 Lanczos 커널은 다음과 같이 정의됩니다.
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
보간된 신호 s2(x, y)는 다음 공식을 사용하여 계산할 수 있습니다.
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
여기서 w(x, y)는 2차원 Lanczos 커널을 사용하여 계산된 정규화 인자입니다.
일부 보간 방법과 달리 Lanczos 커널은 분리 불가능합니다. 즉, 1차원 커널의 곱으로 인수분해할 수 없습니다. 이 속성은 일반적으로 분리 가능한 커널에 비해 계산 비용이 더 높습니다. 성능을 향상시키기 위해 일부 구현에서는 수평 및 수직 차원에 대해 별도의 패스를 수행하여 Lanczos 커널에 근접합니다.
수평 보간:
수직 보간:
수학적 표현:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
정규화 인자 w(x)와 w(y)는 1차원 Lanczos 커널을 사용하여 계산됩니다.
핵심 포인트:
마찬가지로, 텍스처 밉맵을 생성하기 위해 일반적으로 수행되는 것처럼 신호를 여러 번 재귀적으로 리샘플링하면 각 리샘플링 단계에서 오류가 누적되어 이미지 품질이 저하될 수도 있습니다.
Lancos-test 예제를 실행하고 gnuplot을 사용하여 2배로 업샘플링 및 다운샘플링할 때 Lanczos 리샘플링이 간단한 1차원 신호에 어떤 영향을 미치는지 확인하세요.
make
./lanczos-test
gnuplot
> load "output.plot"
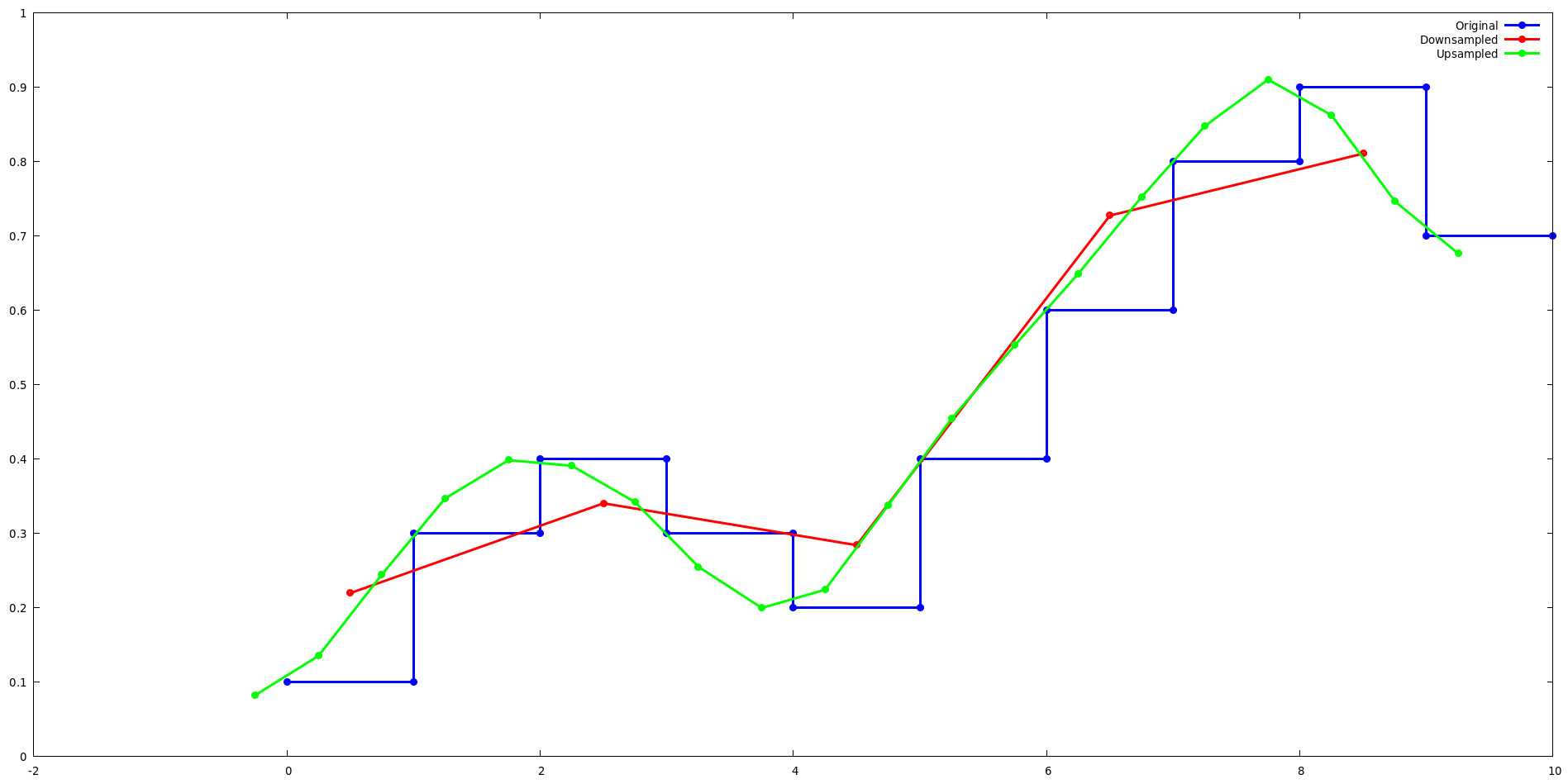
업샘플링:
2의 거듭제곱으로 업샘플링할 때 Lanczos 커널은 2^레벨 값 집합 사이를 순환합니다. 예를 들어, lanzcos-test 업샘플 예제의 처음 4개 출력을 생각해 보세요. L(x)의 출력은 j={0,2} 및 j={1,3}에 대해 반복됩니다.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
다운샘플링:
2의 거듭제곱으로 다운샘플링할 때 Lanczos 커널은 (x - Floor(x))가 위상 변이와 일치하는 상수가 되므로 x와 독립적이 됩니다. 예를 들어, lanzcos-test 다운샘플 예제의 처음 2개 출력을 고려해 보세요. L(x)의 출력은 각 j에 대해 반복됩니다.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
추가 최적화로서 Lanczos 커널은 이러한 경우 값비싼 sinc 함수 계산을 제거하기 위해 미리 계산될 수 있습니다.
이 README는 Google Gemini의 도움으로 작성되었습니다.
추가 참고자료는 다음과 같습니다:
이 코드는 MIT 라이센스에 따라 Jeff Boody에 의해 구현되었습니다.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.