Downcodes의 편집자는 LLM(대형 언어 모델)의 효율성을 향상시키는 혁신적인 기술인 Q-Sparse에 대해 알아보도록 안내합니다. LLM의 강력한 자연어 처리 기능은 많은 주목을 받았지만 높은 계산 비용과 메모리 공간은 실제 응용 프로그램에서 항상 병목 현상을 일으켰습니다. Q-Sparse는 영리한 희소화 방법을 사용하여 모델 성능을 보장하는 동시에 추론 효율성을 크게 향상시켜 LLM을 광범위하게 적용할 수 있는 길을 열어줍니다. 이 기사에서는 Q-Sparse의 핵심 기술, 장점 및 실험적 검증 결과를 심층적으로 살펴보고 LLM의 효율성을 향상시키는 데 큰 잠재력을 보여줍니다.
인공 지능의 세계에서 LLM(대형 언어 모델)은 뛰어난 자연어 처리 기능으로 유명합니다. 그러나 이러한 모델을 실제 응용 프로그램에 배포하는 것은 주로 추론 단계의 높은 계산 비용과 메모리 공간으로 인해 큰 문제에 직면합니다. 이 문제를 해결하기 위해 연구자들은 LLM의 효율성을 향상시키는 방법을 모색해 왔습니다. 최근에는 Q-Sparse라는 방법이 널리 주목을 받고 있습니다.
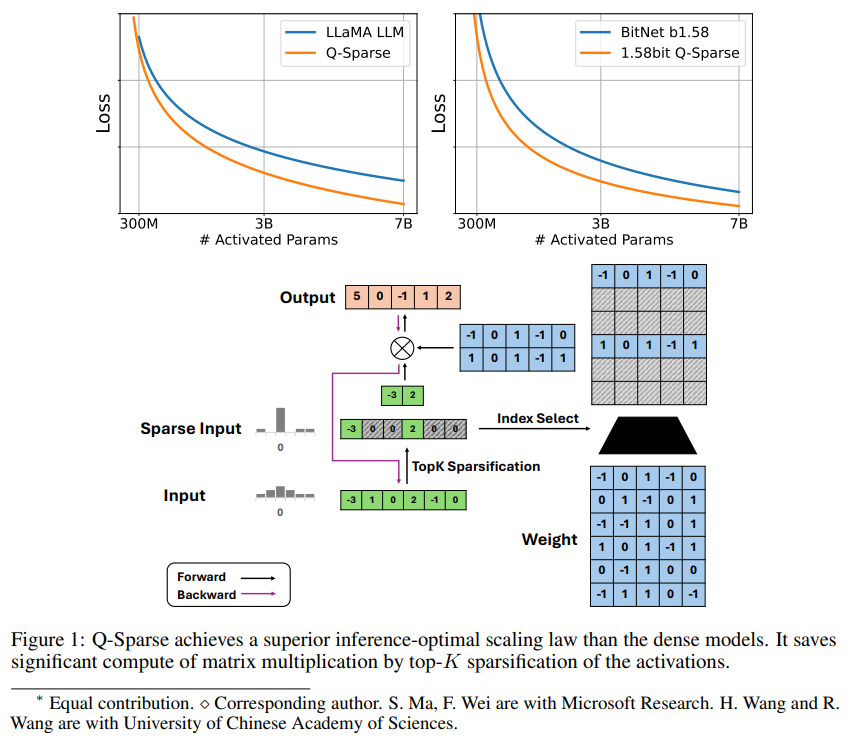
Q-Sparse는 활성화에 top-K 희소화를 적용하고 훈련에 통과 추정기를 적용하여 LLM의 완전 희소 활성화를 달성하는 간단하지만 효과적인 방법입니다. 이는 추론 시 효율성이 크게 향상되었음을 의미합니다. 주요 연구 결과는 다음과 같습니다.
Q-Sparse는 기준선 LLM과 유사한 결과를 유지하면서 더 높은 추론 효율성을 달성합니다.
희소 활성화 LLM에 적합한 추론적 최적 확장 규칙을 제안합니다.
Q-Sparse는 처음부터의 교육, 기성 LLM의 지속적인 교육, 미세 조정 등 다양한 설정에서 작동합니다.
Q-Sparse는 전체 정밀도 및 1비트 LLM(예: BitNet b1.58)에서 작동합니다.
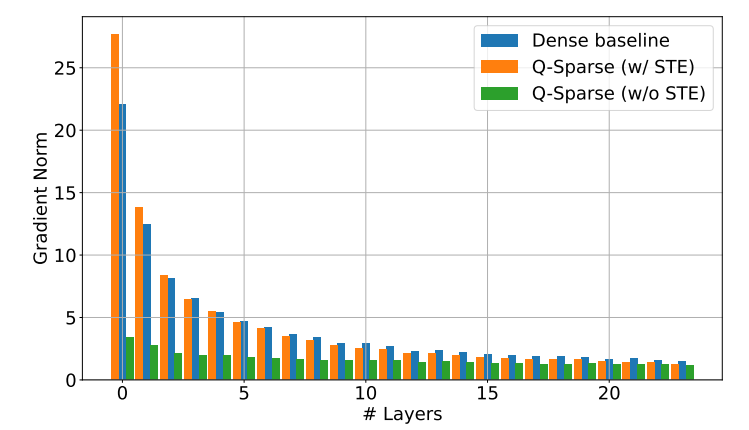
희소 활성화의 장점
희소성은 두 가지 방식으로 LLM의 효율성을 향상시킵니다. 첫째, 희소성은 0 요소가 계산되지 않기 때문에 행렬 곱셈의 계산 양을 줄일 수 있습니다. 둘째, 희소성은 입출력(I/O) 전송 양을 줄일 수 있습니다. 이는 LLM 추론 단계의 주요 병목 현상입니다.
Q-Sparse는 각 선형 투영에 top-K 희소화 함수를 적용하여 활성화의 전체 희소성을 달성합니다. 역전파의 경우 통과 추정기를 사용하여 활성화 기울기를 계산합니다. 또한 활성화 희소성을 더욱 향상시키기 위해 제곱 ReLU 함수가 도입되었습니다.
실험적 검증
연구원들은 일련의 확장 실험을 통해 드물게 활성화된 LLM의 확장 법칙을 연구하고 몇 가지 흥미로운 결과를 얻었습니다.
희소 활성화 모델의 성능은 모델 크기와 희소성 비율이 증가함에 따라 향상됩니다.
고정된 희소성 비율 S가 주어지면 희소 활성화 모델의 성능은 거듭제곱법칙 방식으로 모델 크기 N에 따라 확장됩니다.
고정된 매개변수 N이 주어지면 희소 활성화 모델의 성능은 희소 비율 S에 따라 기하급수적으로 확장됩니다.
Q-Sparse는 처음부터 훈련하는 것뿐만 아니라 기성 LLM의 지속적인 훈련과 미세 조정에도 사용할 수 있습니다. 지속적인 훈련 및 미세 조정 설정에서 연구원들은 처음부터 훈련하는 것과 동일한 아키텍처 및 훈련 프로세스를 사용했습니다. 유일한 차이점은 사전 훈련된 가중치로 모델을 초기화하고 희소 함수를 활성화하여 훈련을 계속한다는 것입니다.
연구원들은 LLM의 효율성을 더욱 향상시키기 위해 1비트 LLM(예: BitNet b1.58) 및 혼합 전문가(MoE)와 함께 Q-Sparse를 사용하는 방법을 모색하고 있습니다. 또한 Q-Sparse를 배치 모드와 호환되도록 만들기 위해 노력하고 있습니다. 이를 통해 LLM 교육 및 추론에 더 많은 유연성을 제공할 수 있습니다.
Q-Sparse 기술의 출현은 LLM의 효율성 문제를 해결하기 위한 새로운 아이디어를 제공하며 컴퓨팅 비용과 메모리 사용량을 줄이는 데 큰 잠재력을 갖고 있으며 더 많은 분야에서 LLM의 적용을 촉진할 것으로 예상됩니다. 앞으로 Q-Sparse를 기반으로 한 더 많은 연구 결과가 등장하여 LLM의 성능과 효율성을 더욱 향상시킬 것으로 믿어집니다.