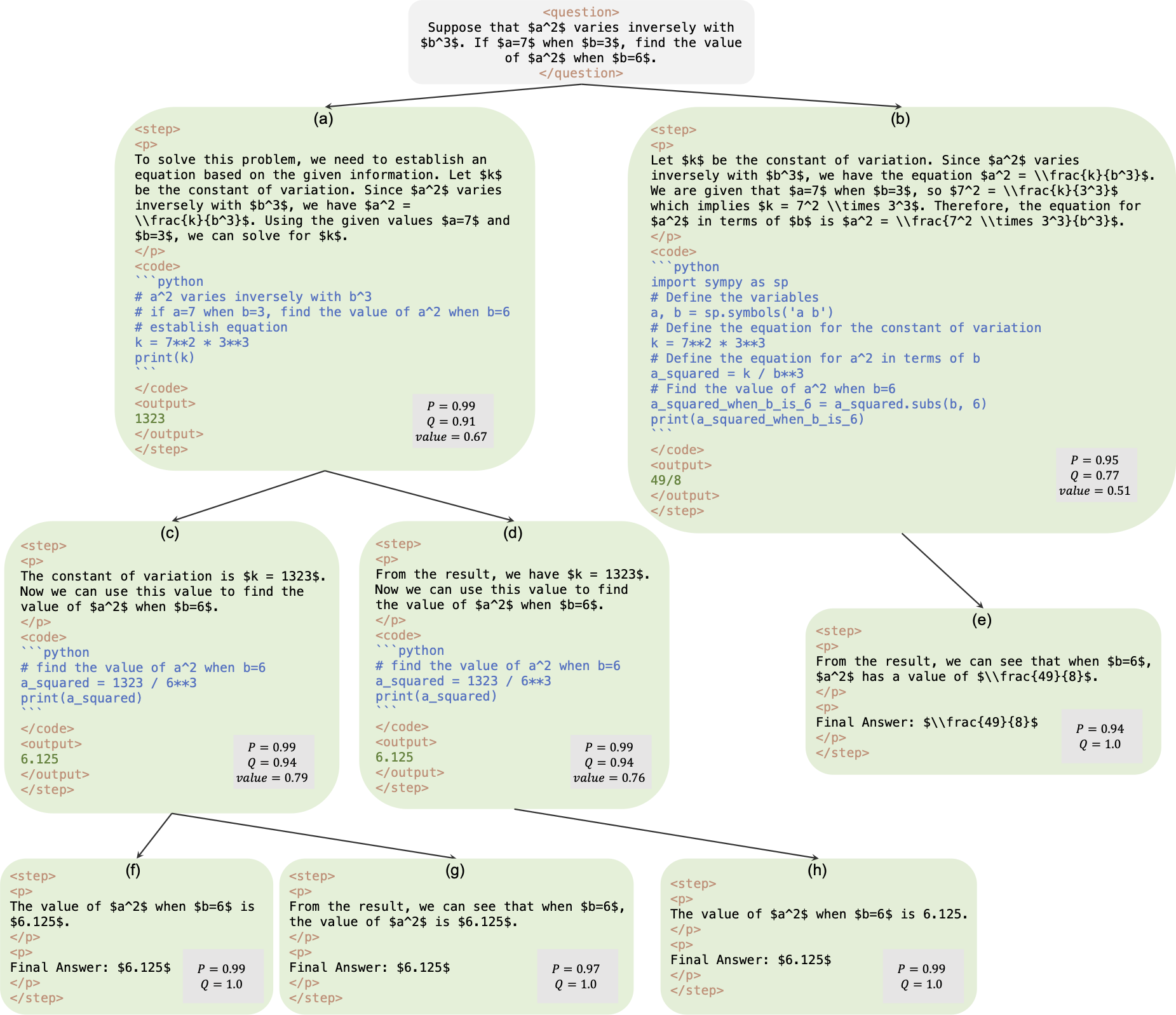
Este é o repositório oficial do artigo AlphaMath Quase Zero: Supervisão de processos sem processo. O código é extraído de nossa base de código corporativa interna. Como resultado, pode haver pequenas diferenças na reprodução dos números relatados em nosso artigo, mas devem ser muito próximas. Nossa abordagem envolve treinar os modelos de política e valor usando apenas o raciocínio matemático derivado da estrutura Monte Carlo Tree Search (MCTS), eliminando a necessidade de GPT-4 ou anotações humanas. Esta é uma ilustração da instância de treinamento gerada pelo MCTS na rodada 3.
Ponto de verificação : AlphaMath-7B rodada 3? / AlphaMath-7B rodada 3?
Conjunto de dados : AlphaMath-Round3-Trainset? O processo de solução dos dados de treinamento é gerado automaticamente com base no MCTS e no ponto de verificação na rodada 2. Exemplos positivos e negativos são incluídos para treinar os modelos de política e valor.
Código de treinamento : Devido à política, só podemos divulgar os detalhes de implementação de algumas funções principais, que basicamente devem ser modificadas em seu próprio código de treinamento.
| Método de Inferência | Precisão | média. tempo (s) por q | média. passos | # sóis |
|---|---|---|---|---|
| Ambicioso | 53,62 | 1.6 | 3.1 | 1 |
| Maj@5 | 61,84 | 2.9 | 2.9 | 5 |
| Viga de nível escalonado (1,5) | 62,32 | 3.1 | 3,0 | primeiro lugar |
| 5 corridas + Maj@5 | 67.04 | x5 | x1 | 5 primeiros-1 |
| Viga de nível escalonado (2,5) | 64,66 | 2.4 | 2.4 | primeiro lugar |
| Viga de nível escalonado (3,5) | 65,74 | 2.3 | 2.2 | primeiro lugar |
| Viga de nível escalonado (5,5) | 65,98 | 4.7 | 2.3 | primeiro lugar |
| 1 corrida + Maj@5 | 66,54 | x1 | x1 | 5 primeiros |
| 5 corridas + Maj@5 | 69,94 | x5 | x1 | 5 primeiros-1 |
| MCTS (N=40) | 64.02 | 10.1 | 3.8 | primeiro lugar |
+ Maj@5 requer execução 5 vezes, o que incentiva a diversidade.+ Maj@5 usa diretamente os 5 candidatos, que carecem de diversidade.| temperatura | 0,6 | 1,0 |
|---|---|---|
| Viga de nível escalonado (1,5) | 62,32 | 62,76 |
| Viga de nível escalonado (2,5) | 64,66 | 65,60 |
| Viga de nível escalonado (3,5) | 65,74 | 66,28 |
| Viga de nível escalonado (5,5) | 65,98 | 66,38 |
Para busca de feixe em nível escalonado, definir temperature=1.0 pode obter resultados ligeiramente melhores.
requirements.txt pip install -r requirements.txt
Ou simplesmente siga os cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py para adicionar o valor head ao LLM. Você pode executar qualquer um dos dois cmds a seguir. Pode haver uma pequena diferença de precisão entre os dois. Na nossa máquina, a primeira obteve 53,4% e a segunda obteve 53,62%.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
ou
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Em nossa máquina, no conjunto de testes MATH, o seguinte cmd com configuração B1=1, B2=5 pode atingir ~62%, e aquele com configuração B1=3, B2=5 pode atingir ~65%.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Calcule a precisão
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
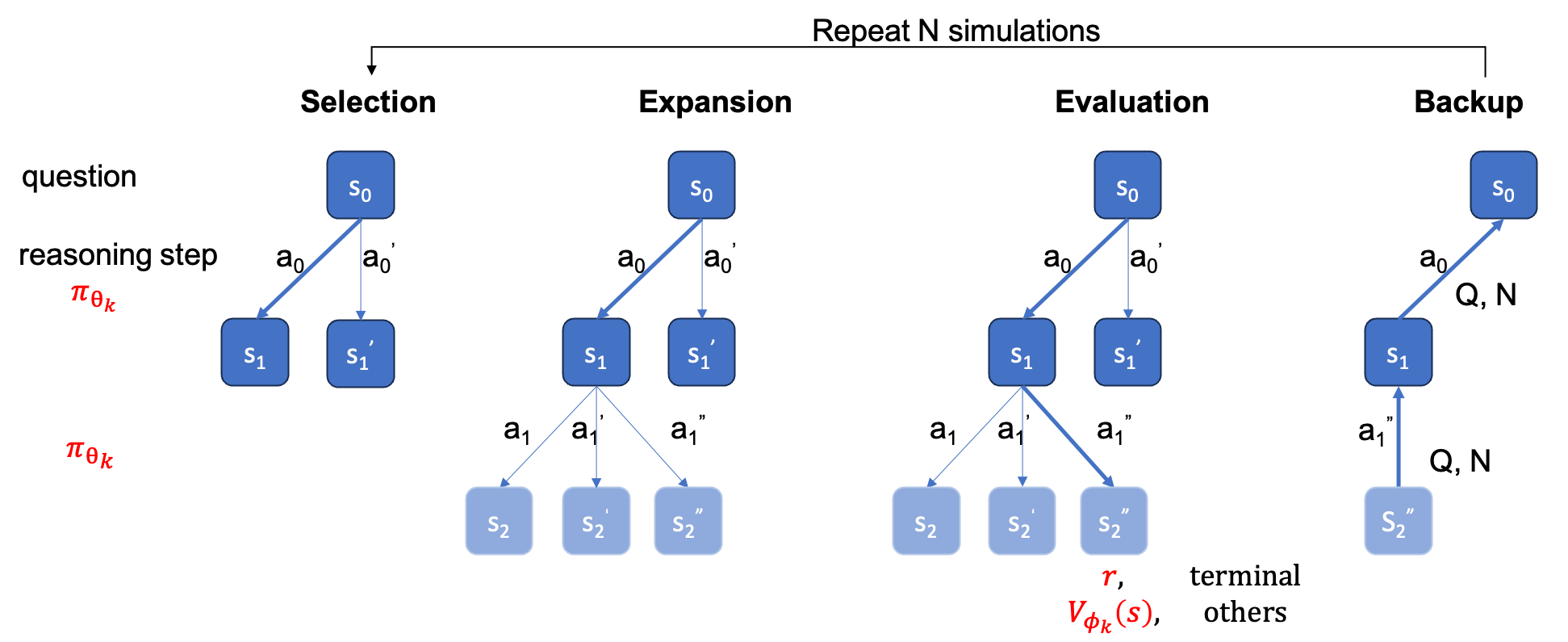
A ground_truth (a resposta final, não o processo de solução) deve ser fornecida no arquivo qaf json ou jsonl (o formato de exemplo pode consultar ../MARIO_EVAL/data/math_testset_annotation.json ).
rodada 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
rodada > 1, após SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
Apenas question será usada para geração da solução, mas o ground_truth será usado para calcular a precisão.
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Diferente da pesquisa de feixe em nível de etapa, você precisa primeiro construir uma árvore completa, depois executar o MCTS off-line e calcular a precisão.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
Nota: este script de avaliação também pode ser executado com árvore salva por pesquisa de feixe em nível de etapa, e a precisão deve permanecer a mesma.
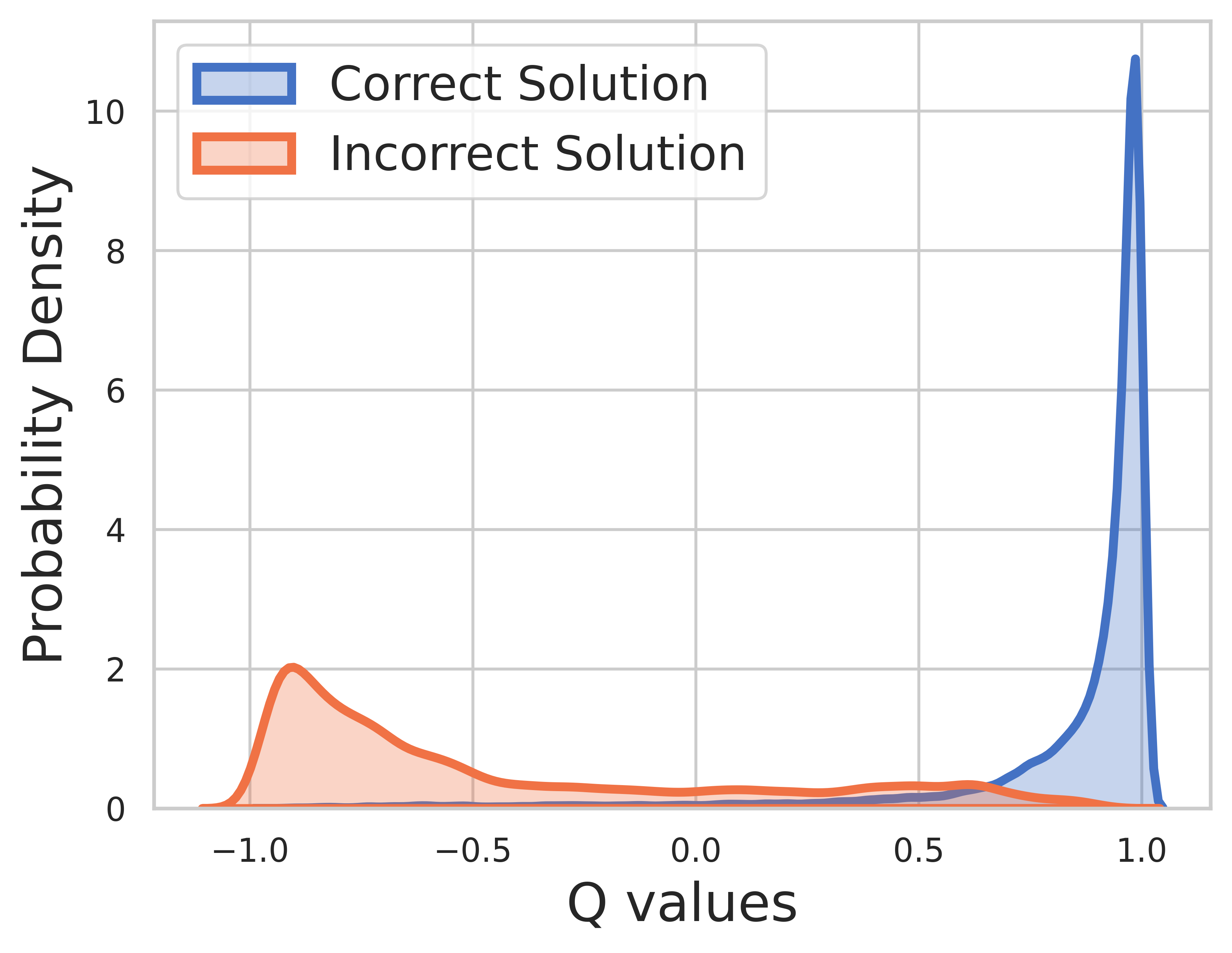
Como a verdade básica é conhecida pelos dados de treinamento, o valor da etapa final é a recompensa e o valor Q pode convergir muito bem.
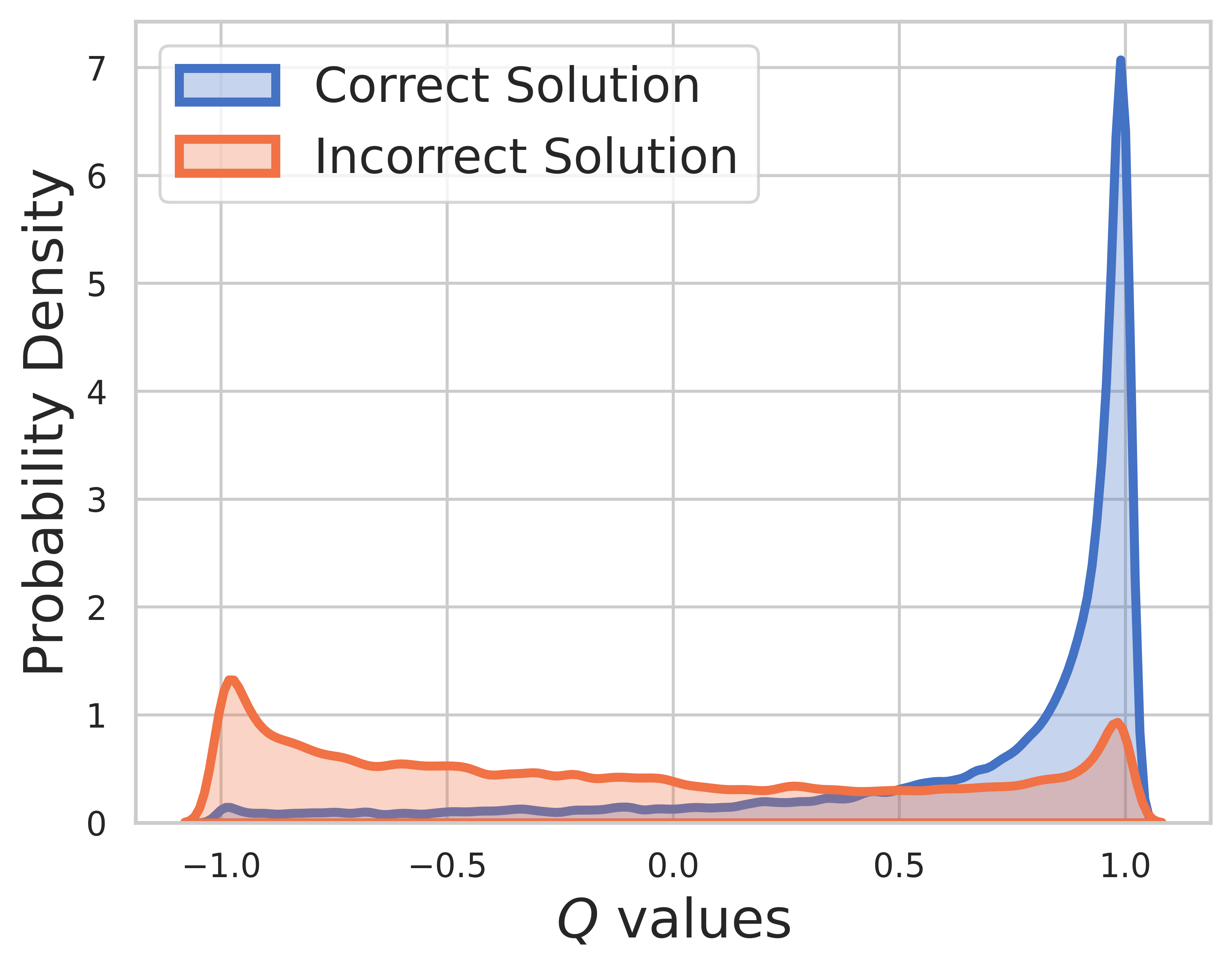
No conjunto de teste, a verdade básica é desconhecida, portanto a distribuição do valor Q inclui etapas intermediárias e finais. A partir desta figura, podemos encontrar
SVPO por MCTS
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
Versão MCTS
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
Kit de ferramentas de avaliação
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
Versão OVM (Modelo de Valor de Resultado)
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}