A reamostragem Lanczos (pronuncia-se Lanchos) é uma técnica sofisticada para interpolar sinais digitais, oferecendo qualidade de imagem superior em comparação com métodos mais simples, como vizinho mais próximo e interpolação bilinear. Ao preservar efetivamente os detalhes e minimizar os artefatos de aliasing, a reamostragem Lanczos é amplamente utilizada em aplicações de processamento de imagens e sinais.
Embora Lanczos seja excelente em qualidade de imagem, isso ocorre ao custo de uma maior complexidade computacional. Além disso, o potencial para artefatos de "toque", especialmente em torno de arestas vivas, pode ser uma desvantagem. Apesar desses desafios, Lanczos continua sendo a escolha preferida para tarefas como dimensionamento e rotação de imagens devido aos seus benefícios gerais de desempenho.
Este documento fornece uma visão abrangente da reamostragem Lanczos, incluindo seus fundamentos teóricos, detalhes de implementação e aplicações práticas. Ele serve como um recurso valioso para desenvolvedores e pesquisadores que buscam compreender e utilizar esta técnica poderosa. As seções subsequentes se aprofundam em aspectos cruciais da reamostragem Lanczos, como o kernel Lanczos, processos de interpolação e reamostragem, preservação de fluxo, aumento, redução da resolução, posicionamento da amostra, faixa de saída, interpolação multidimensional e separabilidade. Um exemplo prático acompanhado de código-fonte está incluído.
O kernel Lanczos, definido para um determinado tamanho de suporte, é uma função usada na reamostragem Lanczos. O kernel é definido como:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
Onde:
A função sinc normalizada é definida como:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
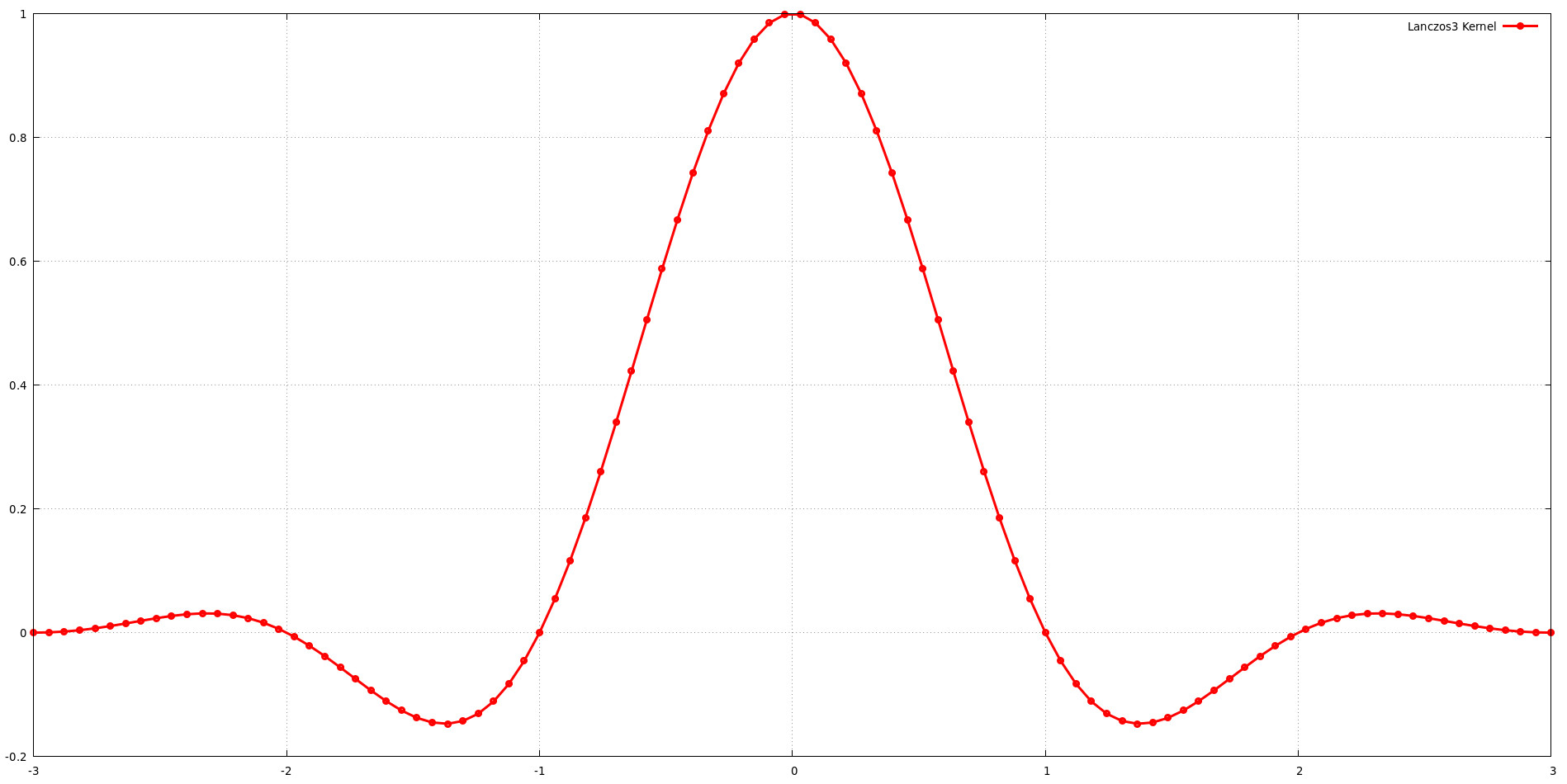
O gráfico ilustra a forma do kernel Lanczos para um tamanho de suporte de a = 3. Isso significa que o kernel inclui três lóbulos da função sinc. Embora o aumento do tamanho do suporte (a) geralmente proporcione mais flexibilidade para moldar a resposta de frequência, também aumenta o custo computacional. Deve-se encontrar um equilíbrio entre qualidade de imagem e eficiência computacional na escolha do tamanho do suporte. A descoberta de Jim Blinn de que o kernel Lanczos com a = 3 oferece um excelente equilíbrio entre preservação de baixa frequência e rejeição de alta frequência apoia esta noção.
Nota: Os termos "largura do kernel", "tamanho do suporte" e "tamanho do filtro" são frequentemente usados de forma intercambiável para descrever o parâmetro a. No entanto, no contexto da reamostragem de Lanczos, o "tamanho do apoio" reflete com mais precisão o conceito.
A interpolação de Lanczos é uma técnica usada para reamostrar um sinal discreto para uma nova taxa de amostragem. Isso é conseguido convolvendo o sinal original com um kernel Lanczos.
O sinal interpolado s2(x) pode ser calculado da seguinte forma:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
Onde:
Preservando o Fluxo:
O fator de normalização w(x) é crucial para preservar a energia ou massa geral do sinal durante o processo de interpolação. Garante que a soma dos valores interpolados se aproxime da soma das amostras originais. O peso do filtro é calculado como:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
Aumento da resolução:
Ao aumentar a taxa de amostragem, a equação de interpolação de Lanczos pode ser usada diretamente sem modificações.
Redução da resolução:
Para evitar artefatos de aliasing ao diminuir a taxa de amostragem, a escala do filtro deve ser ajustada para corresponder à nova taxa de amostragem.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
Onde:
Ao reamostrar um sinal de n1 amostras para n2 amostras, as seguintes posições de amostra são usadas. O índice j é usado para representar as amostras do sinal amostrado s2(x). O termo (j + 0,5) é o centro de uma amostra em s2(x). A etapa escala um ponto em s2(x) para um ponto em s1(x). O termo final -0,5 em x é uma mudança de fase que faz com que as amostras do coeficiente de Lanczos sejam compensadas.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
Ao realizar a interpolação Lanczos, deve-se tomar cuidado especial nos limites do sinal. As técnicas comuns de tratamento de bordas incluem:
Preenchimento zero:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
Fixação:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
A fixação é frequentemente preferida, pois reduz artefatos nas bordas causados por descontinuidades acentuadas perto das bordas. No entanto, a escolha do método de tratamento de bordas depende da aplicação específica e do resultado desejado.
O alcance de s2(x) pode ser maior que o de s1(x) devido aos lóbulos de L(x). Por exemplo, um sinal de entrada s1(x) correspondente a cores de pixel no intervalo de [0,0,1,0] precisa ser fixado no mesmo intervalo para garantir que os valores de saída não excedam quando convertidos novamente em bytes não assinados de [0,255] .
O kernel Lanczos pode ser estendido para múltiplas dimensões para realizar interpolação em imagens ou dados de dimensões superiores.
O kernel Lanczos bidimensional é definido como:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
O sinal interpolado s2(x, y) pode ser calculado usando a seguinte fórmula:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
Onde w(x, y) é o fator de normalização calculado usando o kernel Lanczos bidimensional.
Ao contrário de alguns métodos de interpolação, o kernel Lanczos é inseparável, o que significa que não pode ser fatorado no produto de kernels unidimensionais. Esta propriedade geralmente leva a custos computacionais mais elevados em comparação com kernels separáveis. Para melhorar o desempenho, algumas implementações aproximam o kernel Lanczos realizando passagens separadas para as dimensões horizontal e vertical.
Interpolação horizontal:
Interpolação vertical:
Representação Matemática:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
Observe que os fatores de normalização w(x) e w(y) são calculados usando o kernel Lanczos unidimensional.
Pontos-chave:
Da mesma forma, a reamostragem recursiva de um sinal várias vezes, como comumente feito para gerar mipmaps de textura, também pode degradar a qualidade da imagem devido ao acúmulo de erros de cada etapa de reamostragem.
Execute o exemplo lancos-test e use o gnuplot para ver como a reamostragem de Lanczos afeta um sinal unidimensional simples quando aumentado e diminuído por um fator de 2.
make
./lanczos-test
gnuplot
> load "output.plot"
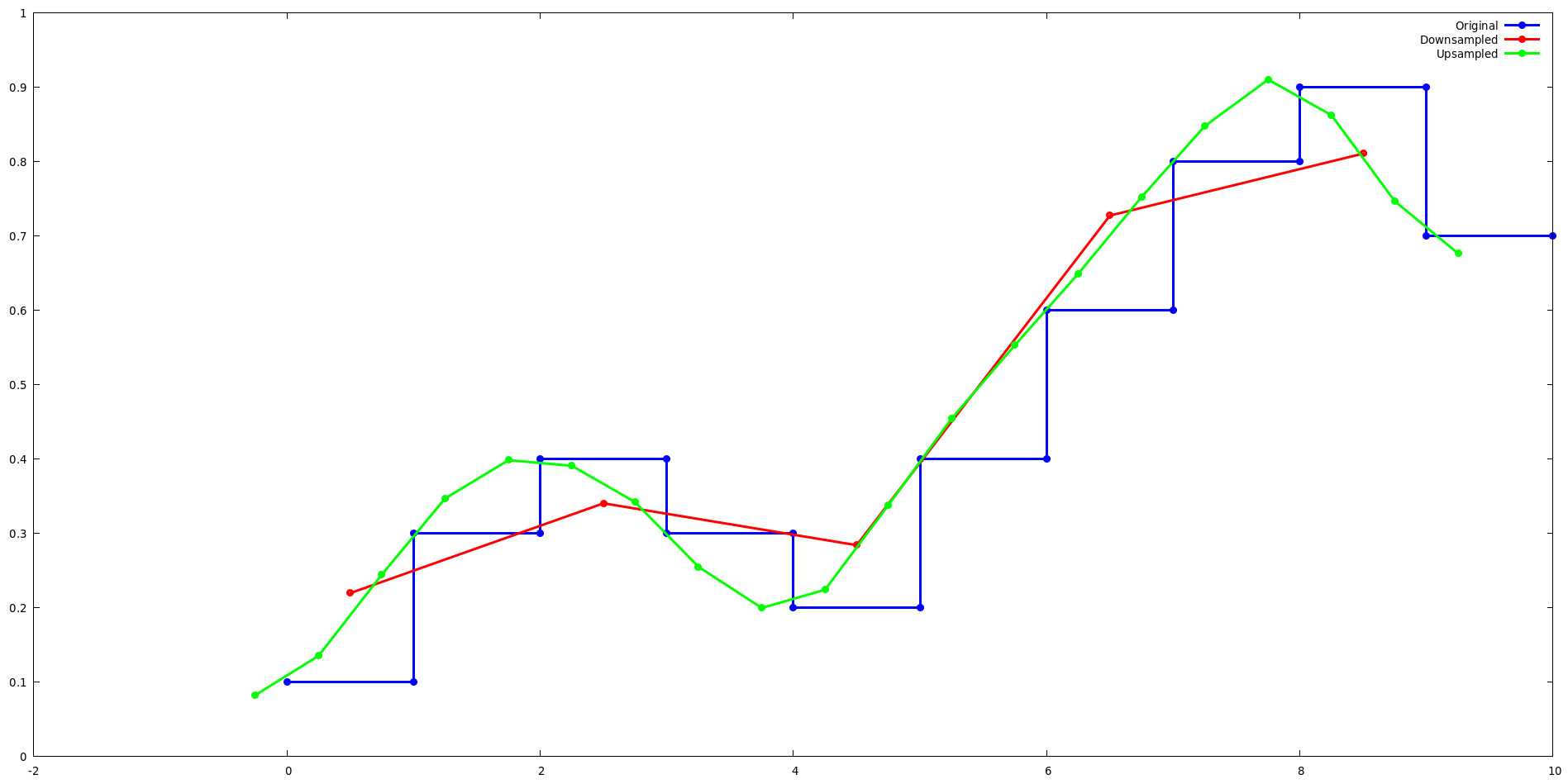
Aumento da resolução:
Ao aumentar a resolução por uma potência de dois, o kernel Lanczos alterna entre conjuntos de valores de 2 níveis. Por exemplo, considere as primeiras 4 saídas do exemplo de upsample lanzcos-test. Observe que as saídas para L(x) se repetem para j={0,2} e j={1,3}.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
Redução da resolução:
Ao reduzir a resolução por uma potência de dois, o kernel Lanczos torna-se independente de x, uma vez que (x - floor(x)) se torna uma constante que corresponde à mudança de fase. Por exemplo, considere as duas primeiras saídas do exemplo de redução da amostragem lanzcos-test. Observe que as saídas de L(x) se repetem para cada j.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
Como uma otimização adicional, o kernel Lanczos pode ser pré-computado para esses casos para eliminar o caro cálculo da função sinc.
Este README foi criado com a ajuda do Google Gemini.
Referências adicionais incluem:
Este código foi implementado por Jeff Boody sob a licença do MIT.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.