GGS

GGS

Greedy Gaussian Segmentation (GGS) é um solucionador Python para segmentar com eficiência dados de séries temporais multivariadas. Para obter detalhes de implementação, consulte nosso artigo em http://stanford.edu/~boyd/papers/ggs.html.

---

O GGS Solver pega uma matriz de dados n por T e quebra os carimbos de data e hora T em um vetor n-dimensional em segmentos sobre os quais os dados são bem explicados como amostras independentes de uma distribuição gaussiana multivariada. Ele faz isso formulando um problema de máxima verossimilhança regulado por covariância e resolvendo-o usando uma heurística gananciosa, com detalhes completos descritos no artigo.

Baixar e configurar

1. Baixe o código fonte no terminal executando:

 git clone [email protected]:davidhallac/GGS.git

2. Confirme se o código foi baixado corretamente executando:

 cd GGS
python helloworld.py

3. Para escrever sua própria função Python que usa ggs, simplesmente certifique-se de que ggs.py esteja no mesmo diretório do seu novo arquivo e adicione o seguinte código ao início do seu script:

 from ggs import *

Funções suportadas

O pacote GGS tem três funções principais:

 bps, objectives = GGS(data, Kmax, lamb)

Encontra K pontos de interrupção nos dados para um determinado parâmetro de regularização lambda

Entradas

dados - uma matriz de dados n por T, com carimbos de data e hora T de um vetor n-dimensional

Kmax - o número de pontos de interrupção a serem encontrados

lamb - parâmetro de regularização para a covariância regularizada

Devoluções

bps - Lista de listas, onde o elemento i da lista maior é o conjunto de pontos de interrupção encontrados em K = i no algoritmo GGS

objetivos - Lista dos valores objetivos em cada etapa intermediária (para K = 0 a Kmax)

---

 meancovs = GGSMeanCov(data, breakpoints, lamb)

Encontra as médias e covariâncias regularizadas de cada segmento, dado um conjunto de pontos de interrupção.

Entradas

dados - uma matriz de dados n por T, com carimbos de data e hora T de um vetor n-dimensional

pontos de interrupção - uma lista de locais de pontos de interrupção

lamb - parâmetro de regularização para a covariância regularizada

Devoluções

meancovs - uma lista de tuplas (média, covariância) para cada segmento nos dados

---

 cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])

Executa validação cruzada de 10 vezes e retorna a probabilidade do conjunto de treinamento e teste para cada par (K, lambda) até Kmax

Entradas

dados - uma matriz de dados n por T, com carimbos de data e hora T de um vetor n-dimensional

Kmax - o número máximo de pontos de interrupção para executar o GGS

lambList – uma lista de parâmetros de regularização para testar

Devoluções

cvResults - lista de tuplas (lamb, ([TrainLL],[TestLL])) para cada parâmetro de regularização em lambList. Aqui, TrainLL e TestLL são a probabilidade média de log por amostra nas 10 dobras de validação cruzada para todos os K de 0 a Kmax

---

Parâmetros opcionais adicionais (para todas as três funções acima):

features = [] - selecione um determinado subconjunto de colunas nos dados para operar

verbose = False – Imprime etapas intermediárias ao executar o algoritmo

Exemplo de uso

A execução de financeExample.py produzirá o seguinte gráfico, mostrando o objetivo (Equação 4 no artigo) versus o número de pontos de interrupção:

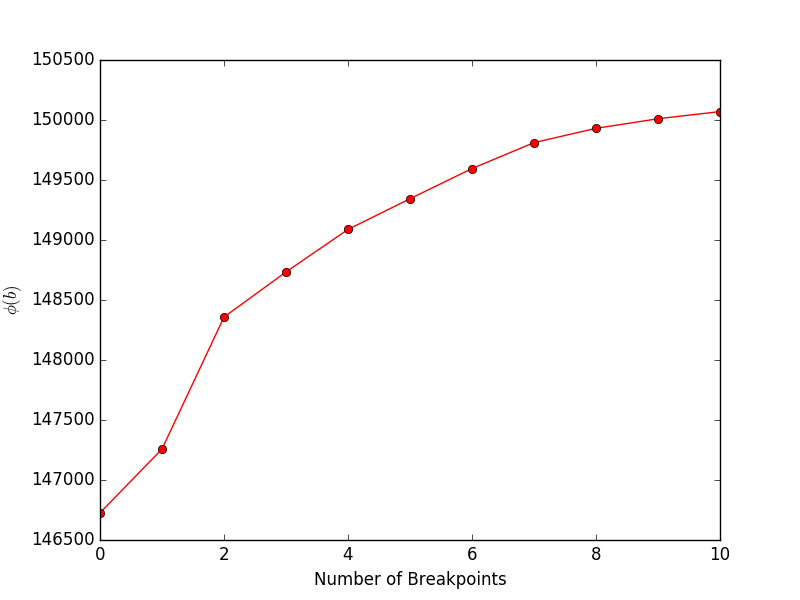
Depois de resolvermos as localizações dos pontos de interrupção, podemos usar a função FindMeanCovs() para encontrar as médias e covariâncias de cada segmento. No exemplo em helloworld.py , traçar as médias, variações e covariâncias dos três sinais produz:

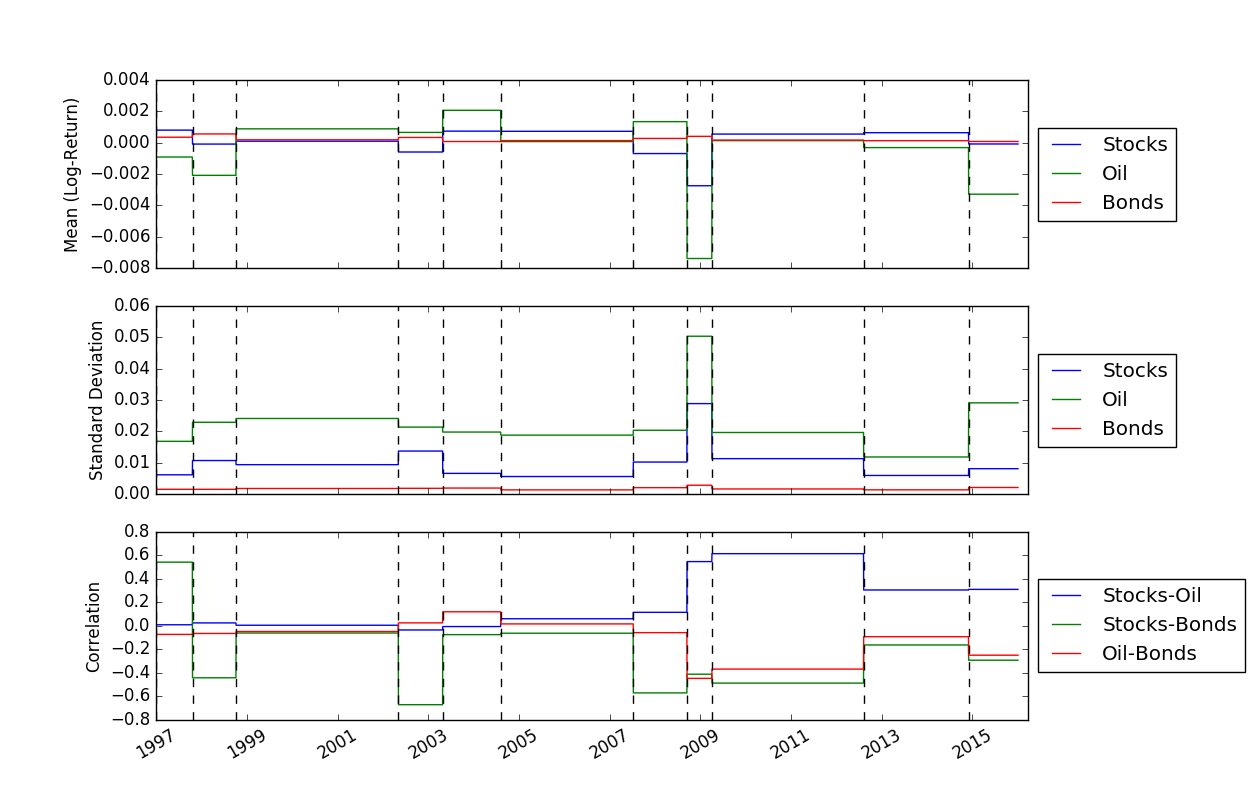
Para executar a validação cruzada, que pode ser útil na determinação dos valores ideais de K e lambda, podemos usar o código a seguir para carregar os dados, executar a validação cruzada e, em seguida, traçar o teste e treinar a probabilidade:

 from ggs import *
import numpy as np
import matplotlib.pyplot as plt

filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]

#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)

trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()

O gráfico resultante se parece com:

Referências

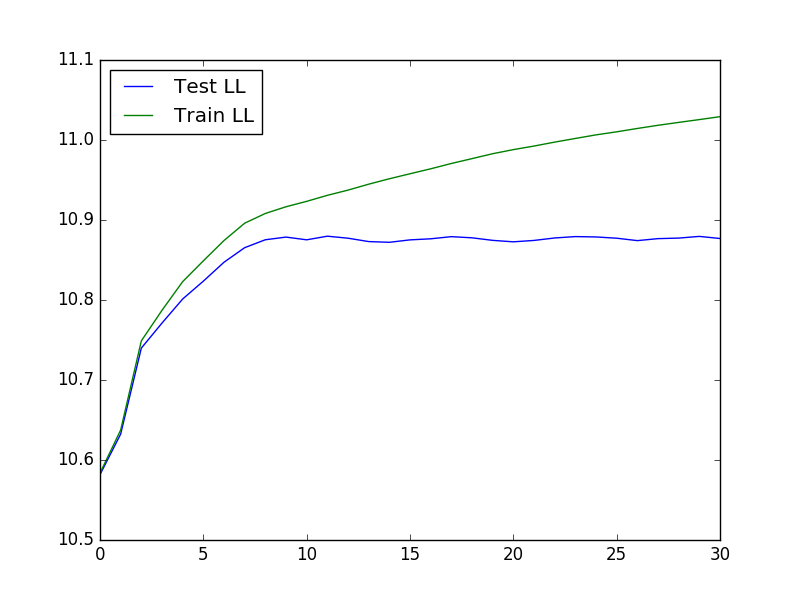
Segmentação gaussiana gananciosa de dados de séries temporais - D. Hallac, P. Nystrup e S. Boyd

Autores

David Hallac, Peter Nystrup e Stephen Boyd.