Bosonic é uma biblioteca desenvolvida para simulação de sistemas fotônicos cujas entradas são bósons indistinguíveis (no caso de interesse dos autores, fótons). Em particular, concentra-se no cálculo rápido das funções de transferência de múltiplas partículas para estes sistemas e suporta o cálculo do gradiente de uma função de custo em relação aos parâmetros do sistema. Ele foi originalmente desenvolvido para o desenvolvimento de nossas Redes Neurais Ópticas Quânticas [1] e contém funcionalidades especializadas para sua simulação e otimização.
Os principais focos desta biblioteca eram duplos:
A principal motivação para este pacote foi o cálculo rápido da transformada unitária de múltiplas partículas em função da unitária de partícula única e do número de entradas bosônicas. Ou seja, se tivermos um U unitário quadridimensional e soubermos que há 3 fótons na entrada, queremos saber a transformação ao longo do
Isso é suportado pela função bosonic.aa_phi , que leva o nome de Aaronson e Arkhipov, que especificaram a forma desta função que usamos como sua função Φ(U) em [2]. Por exemplo, podemos demonstrar o famoso efeito Hong-Ou-Mandel com um divisor de feixe:
>> > import bosonic as b
>> > import numpy as np
>> > U = np . array ([[ 1 , 1 ], [ 1 , - 1 ]], dtype = complex ) / np . sqrt ( 2 )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU )
[[ 0.5 + 0.j 0.70710678 + 0.j 0.5 + 0.j ]
[ 0.70710678 + 0.j 0. + 0.j - 0.70710678 + 0.j ]
[ 0.5 + 0.j - 0.70710678 + 0.j 0.5 + 0.j ]]
>> > print ( b . fock . basis ( 2 , 2 ))
[[ 2 , 0 ], [ 1 , 1 ], [ 0 , 2 ]]
>> > input = np . array ([[ 0 ], [ 1 ], [ 0 ]], dtype = complex )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU . dot ( input ))
[[ 0.70710678 + 0.j ]
[ 0. + 0.j ]
[ - 0.70710678 + 0.j ]]
>> > print ( np . abs ( phiU . dot ( input )) ** 2 )
[[ 0.5 ]
[ 0. ]
[ 0.5 ]]Aqui, construímos o unitário correspondente a um divisor de feixe 50/50 em U. Conforme mostrado na linha após imprimirmos phiU, a base aqui é [2, 0], [1, 1] e [0, 2]. Portanto, o estado correspondente a um fóton incidente em cada uma das entradas é [0, 1, 0]. Na linha final, duas linhas, vemos que a saída é uma superposição igual sobre dois fótons em uma saída e dois fótons na outra, sem probabilidade de os fótons saírem por portas diferentes.
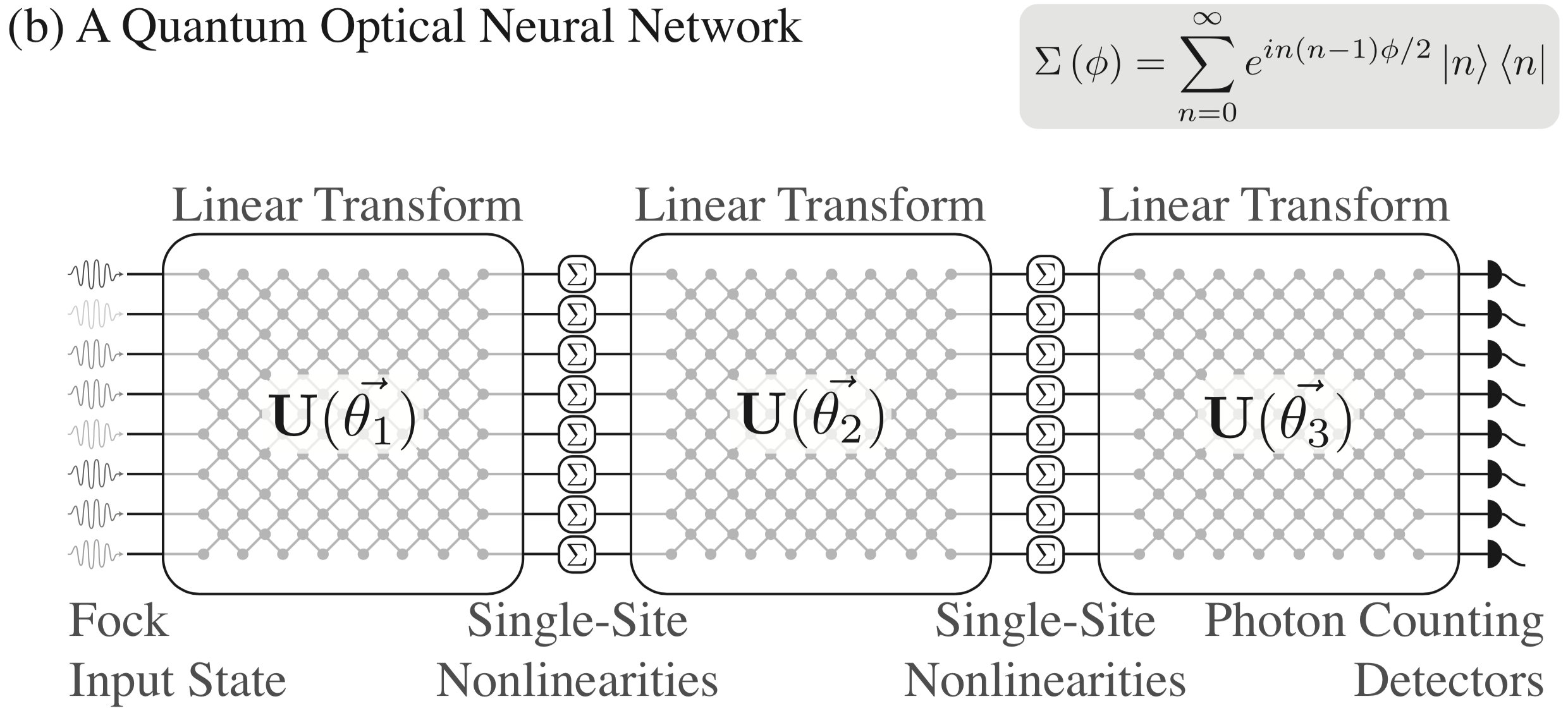
Conforme descrito em [1], desenvolvemos uma arquitetura proposta para redes neurais ópticas quânticas que envolve o agrupamento de transformações unitárias arbitrárias com não-linearidades de sítio único. Veja o artigo para mais detalhes, mas aqui está um resumo visual da arquitetura:
Clonar este repositório é atualmente a única maneira de obter bosonic em seu sistema. Antes de fazer isso, você precisará do pacote python Cython instalado para construir bosonic corretamente. Algo assim deve funcionar no Linux (usando seu gerenciador de pacotes python preferido em vez de pip , se desejar):
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ pip install .No Mac, você também precisará do gcc do homebrew e do libopenmp:
$ brew install gcc
$ brew install libomp
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ CC=gcc-8 pip install . Você poderá então testar se bosonic está instalado corretamente executando
$ python setup.py test[1] Steinbrecher, GR, Olson, JP, Englund, D. e Carolan, J. (2018). Redes neurais ópticas quânticas. Pré-impressão do arXiv arXiv:1808.10047. https://arxiv.org/abs/1808.10047
[2] Aaronson, Scott e Alex Arkhipov. "A complexidade computacional da óptica linear." Anais do quadragésimo terceiro simpósio anual da ACM sobre Teoria da Computação. ACM, 2011. https://arxiv.org/pdf/1011.3245.pdf