Tesla Stock Price Prediction

Análise de série temporal

• Previsão de ações da Tesla por modelos de série temporal Obtendo informações sobre ações da Tesla Company (NASDAQ: TSLA) por meio do Yahoo Finance. Este projeto aplicará os métodos de análise de séries temporais para investigar as informações básicas do TSLA e decompor as séries temporais do TLSA.
• Os métodos de suavização exponencial para prever o preço do TSLA nos próximos 365 dias e depois usarão
• O modelo ARIMA para prever o preço. Este projeto também irá verificar a distribuição do erro de previsão para verificar o desempenho do modelo.

Decompor a série temporal

Decompor uma série temporal significa separá-la nas suas componentes constituintes, que normalmente são uma componente de tendência e uma componente irregular, e se for uma série temporal sazonal, uma componente sazonal. Para as informações das ações da TSLA, a partir do gráfico de tendência de preços, podemos ver que não há componente sazonal nos dados. Mas estes dados de série temporal devem incluir uma componente de tendência e uma componente irregular. A decomposição da série temporal envolve tentar separar a série temporal nestas componentes, ou seja, estimar a componente de tendência e a componente irregular. Iremos a função SMA() para suavizar os dados TSLA. Escolheremos a ordem diferente (n=8 en=40) para verificar o componente de tendência. O objetivo é tentar suavizar os dados com uma média móvel simples.

Modelo de Previsão e Avaliação: Suavização Exponencial

• Modelo de suavização exponencial
  O modelo de suavização exponencial pode ser usado para fazer previsões de curto prazo para dados de séries temporais. A partir dos dados do TSLA, sabemos que pode ser descrito como o modelo aditivo sem sazonalidade. No gráfico de tendências, podemos ver que as flutuações aleatórias nas séries temporais parecem ter tamanho aproximadamente constante ao longo do tempo. Portanto, usaremos a função HoltWinter() para ajustar uma previsão simples de suavização exponencial.

Modelo de Previsão e Avaliação: Modelo ARIMA

Modelo ARIMA

ARIMA (Média Móvel Integrada Autoregressiva) é uma ferramenta importante usada na análise de séries temporais para tentar prever valores futuros de uma variável com base em seu valor presente. Equação de previsão ARIMA(p,d,q): Os modelos ARIMA são, em teoria, a classe mais geral de modelos para previsão de uma série temporal que pode ser tornada “estacionária” por diferenciação. Os modelos ARIMA são definidos para séries temporais estacionárias. Portanto, se você começar com uma série temporal não estacionária, primeiro precisará “diferenciar” a série temporal até obter uma série temporal estacionária. Para diferenciar as séries temporais d vezes para obter uma série estacionária, usamos a função diff(). Em seguida utilizaremos o teste ADF formal que não rejeita a hipótese nula de não estacionariedade, confirmando nossa inspeção visual:

Resumo

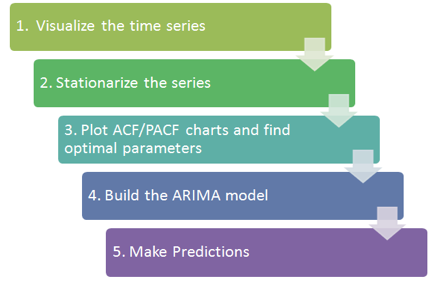
Nesta seção, usamos os dados de ações da TESLA como séries temporais. Nós o decompomos e usamos a suavização exponencial HoltWinter e ARIMA para prever o preço futuro das ações. Os procedimentos básicos são os da figura a seguir.

A outra coisa é que devemos sempre analisar os erros e ajustar os parâmetros do modelo para obter melhores resultados.