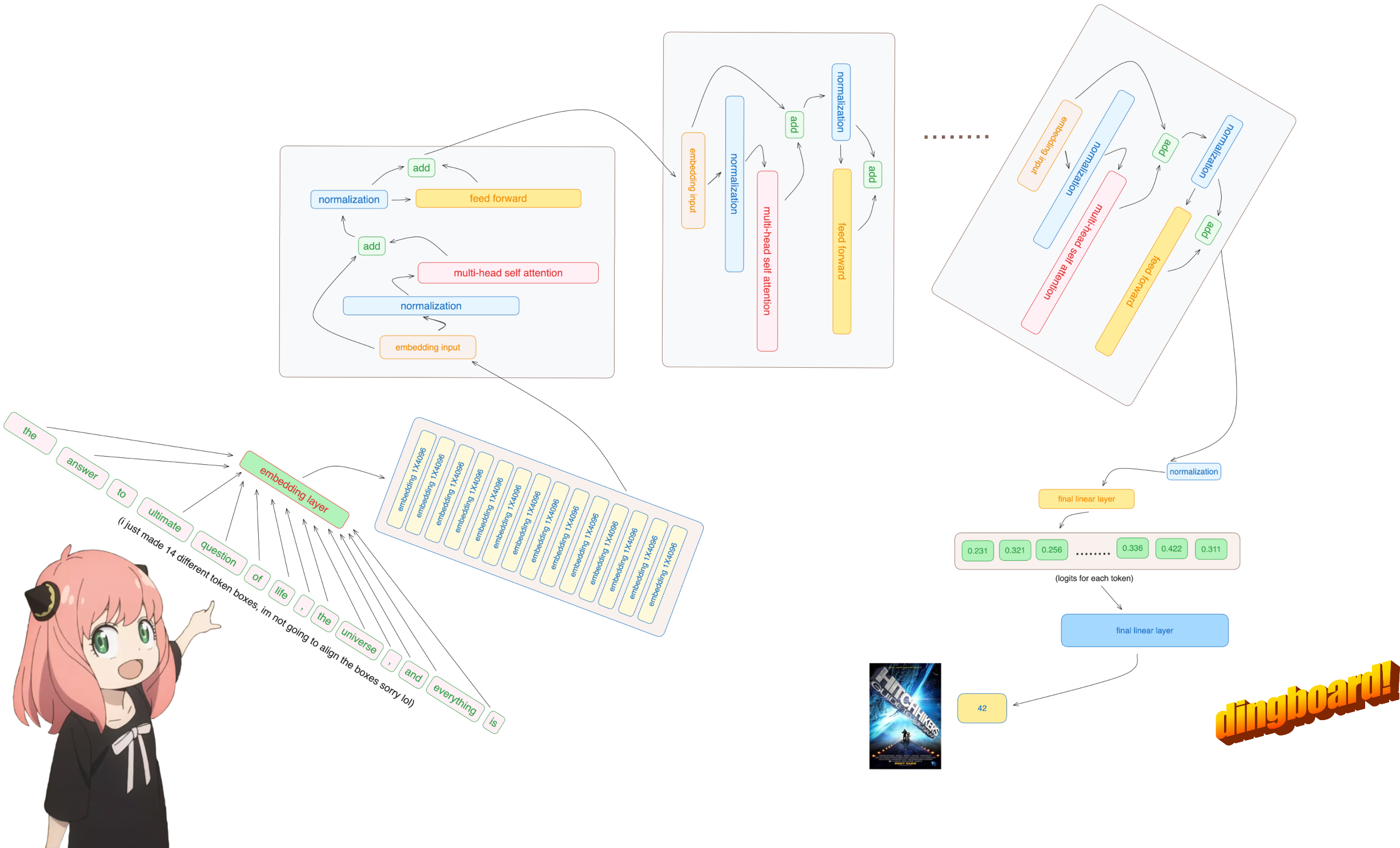
neste arquivo, implementei o llama3 do zero, um tensor e multiplicação de matrizes por vez.
Além disso, vou carregar tensores diretamente do arquivo de modelo fornecido pelo meta para llama3. Você precisa baixar os pesos antes de executar este arquivo. aqui está o link oficial para baixar os pesos: https://llama.meta.com/llama-downloads/
não vou implementar um tokenizer bpe (mas andrej karpathy tem uma implementação realmente limpa)
link para sua implementação: https://github.com/karpathy/minbpe
from pathlib import Path
import tiktoken
from tiktoken . load import load_tiktoken_bpe
import torch
import json
import matplotlib . pyplot as plt
tokenizer_path = "Meta-Llama-3-8B/tokenizer.model"
special_tokens = [
"<|begin_of_text|>" ,
"<|end_of_text|>" ,
"<|reserved_special_token_0|>" ,
"<|reserved_special_token_1|>" ,
"<|reserved_special_token_2|>" ,
"<|reserved_special_token_3|>" ,
"<|start_header_id|>" ,
"<|end_header_id|>" ,
"<|reserved_special_token_4|>" ,
"<|eot_id|>" , # end of turn
] + [ f"<|reserved_special_token_ { i } |>" for i in range ( 5 , 256 - 5 )]
mergeable_ranks = load_tiktoken_bpe ( tokenizer_path )
tokenizer = tiktoken . Encoding (
name = Path ( tokenizer_path ). name ,
pat_str = r"(?i:'s|'t|'re|'ve|'m|'ll|'d)|[^rnp{L}p{N}]?p{L}+|p{N}{1,3}| ?[^sp{L}p{N}]+[rn]*|s*[rn]+|s+(?!S)|s+" ,
mergeable_ranks = mergeable_ranks ,
special_tokens = { token : len ( mergeable_ranks ) + i for i , token in enumerate ( special_tokens )},
)
tokenizer . decode ( tokenizer . encode ( "hello world!" )) 'hello world!'
normalmente, a leitura disso depende de como as classes do modelo são escritas e dos nomes das variáveis dentro delas.
mas como estamos implementando o llama3 do zero, leremos o arquivo um tensor de cada vez.
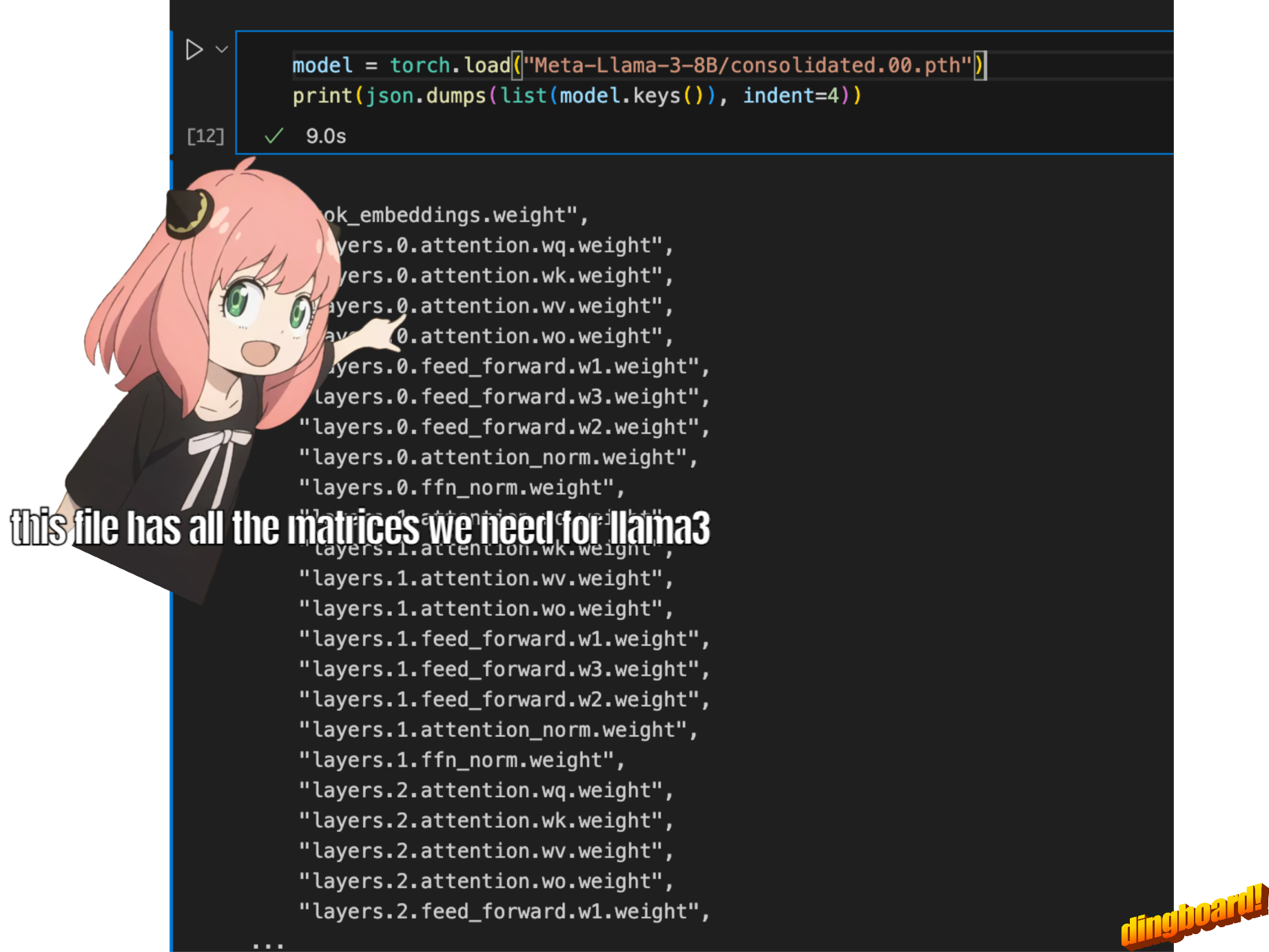
model = torch . load ( "Meta-Llama-3-8B/consolidated.00.pth" )
print ( json . dumps ( list ( model . keys ())[: 20 ], indent = 4 )) [
"tok_embeddings.weight",
"layers.0.attention.wq.weight",
"layers.0.attention.wk.weight",
"layers.0.attention.wv.weight",
"layers.0.attention.wo.weight",
"layers.0.feed_forward.w1.weight",
"layers.0.feed_forward.w3.weight",
"layers.0.feed_forward.w2.weight",
"layers.0.attention_norm.weight",
"layers.0.ffn_norm.weight",
"layers.1.attention.wq.weight",
"layers.1.attention.wk.weight",
"layers.1.attention.wv.weight",
"layers.1.attention.wo.weight",
"layers.1.feed_forward.w1.weight",
"layers.1.feed_forward.w3.weight",
"layers.1.feed_forward.w2.weight",
"layers.1.attention_norm.weight",
"layers.1.ffn_norm.weight",
"layers.2.attention.wq.weight"
]
with open ( "Meta-Llama-3-8B/params.json" , "r" ) as f :
config = json . load ( f )
config {'dim': 4096,
'n_layers': 32,
'n_heads': 32,
'n_kv_heads': 8,
'vocab_size': 128256,
'multiple_of': 1024,
'ffn_dim_multiplier': 1.3,
'norm_eps': 1e-05,
'rope_theta': 500000.0}
dim = config [ "dim" ]
n_layers = config [ "n_layers" ]
n_heads = config [ "n_heads" ]
n_kv_heads = config [ "n_kv_heads" ]
vocab_size = config [ "vocab_size" ]
multiple_of = config [ "multiple_of" ]
ffn_dim_multiplier = config [ "ffn_dim_multiplier" ]
norm_eps = config [ "norm_eps" ]
rope_theta = torch . tensor ( config [ "rope_theta" ])aqui usamos tiktoken (acho que uma biblioteca openai) como tokenizer
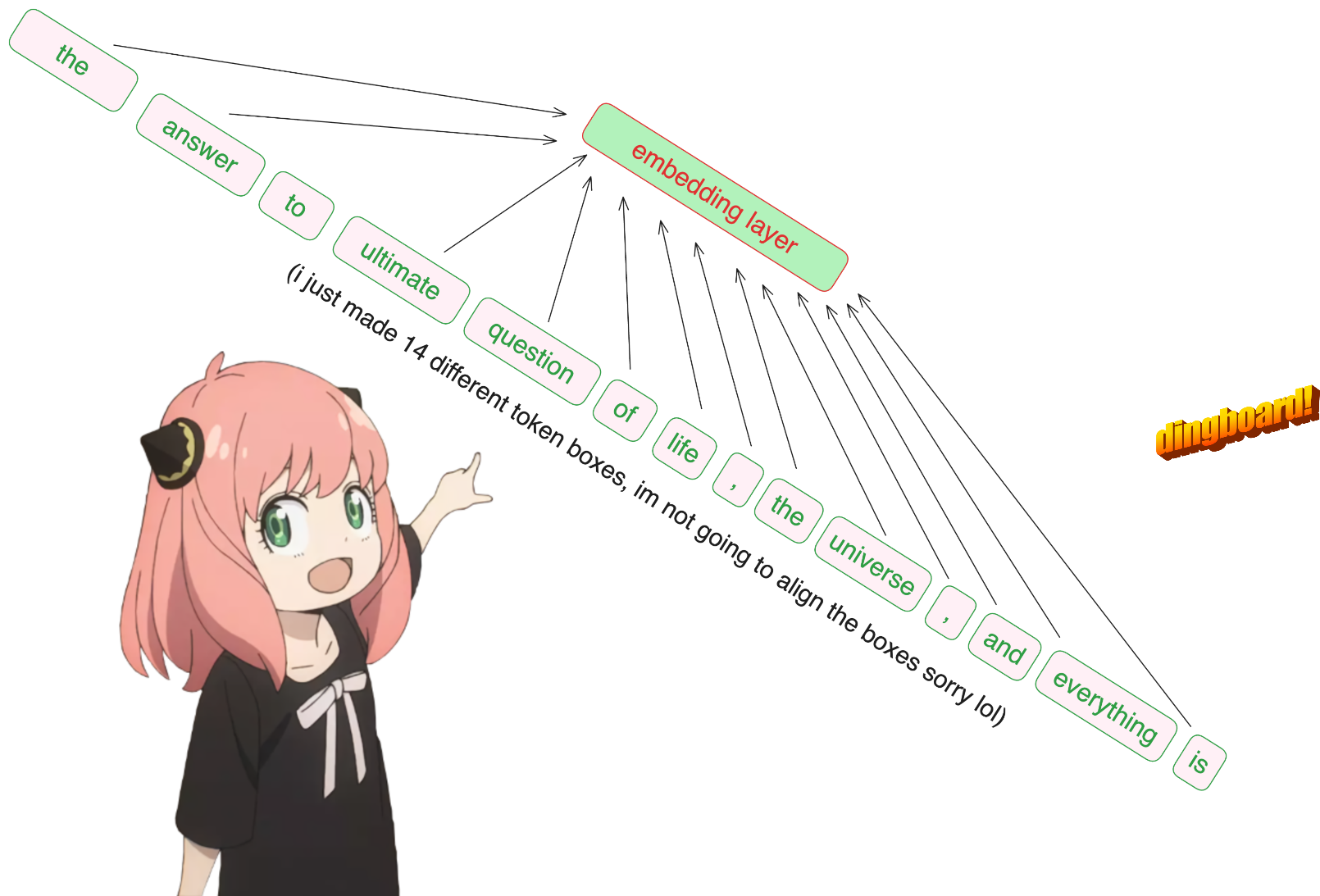
prompt = "the answer to the ultimate question of life, the universe, and everything is "
tokens = [ 128000 ] + tokenizer . encode ( prompt )
print ( tokens )
tokens = torch . tensor ( tokens )
prompt_split_as_tokens = [ tokenizer . decode ([ token . item ()]) for token in tokens ]
print ( prompt_split_as_tokens ) [128000, 1820, 4320, 311, 279, 17139, 3488, 315, 2324, 11, 279, 15861, 11, 323, 4395, 374, 220]
['<|begin_of_text|>', 'the', ' answer', ' to', ' the', ' ultimate', ' question', ' of', ' life', ',', ' the', ' universe', ',', ' and', ' everything', ' is', ' ']
DESCULPE, mas esta é a única parte da base de código onde uso um módulo de rede neural embutido
de qualquer forma, nossos tokens [17x1] agora são [17x4096], ou seja, 17 embeddings (um para cada token) de comprimento 4096
nota: acompanhe as formas, fica muito mais fácil entender tudo

embedding_layer = torch . nn . Embedding ( vocab_size , dim )
embedding_layer . weight . data . copy_ ( model [ "tok_embeddings.weight" ])
token_embeddings_unnormalized = embedding_layer ( tokens ). to ( torch . bfloat16 )
token_embeddings_unnormalized . shape torch.Size([17, 4096])
por favor, observe que após esta etapa as formas não mudam, os valores são apenas normalizados
coisas para ter em mente, precisamos de um norm_eps (da configuração) porque não queremos definir acidentalmente rms como 0 e dividir por 0
aqui está a fórmula:

# def rms_norm(tensor, norm_weights):
# rms = (tensor.pow(2).mean(-1, keepdim=True) + norm_eps)**0.5
# return tensor * (norm_weights / rms)
def rms_norm ( tensor , norm_weights ):
return ( tensor * torch . rsqrt ( tensor . pow ( 2 ). mean ( - 1 , keepdim = True ) + norm_eps )) * norm_weights você me verá acessando layer.0 do model dict (esta é a primeira camada)
de qualquer maneira, depois de normalizar nossas formas ainda são [17x4096] iguais à incorporação, mas normalizadas
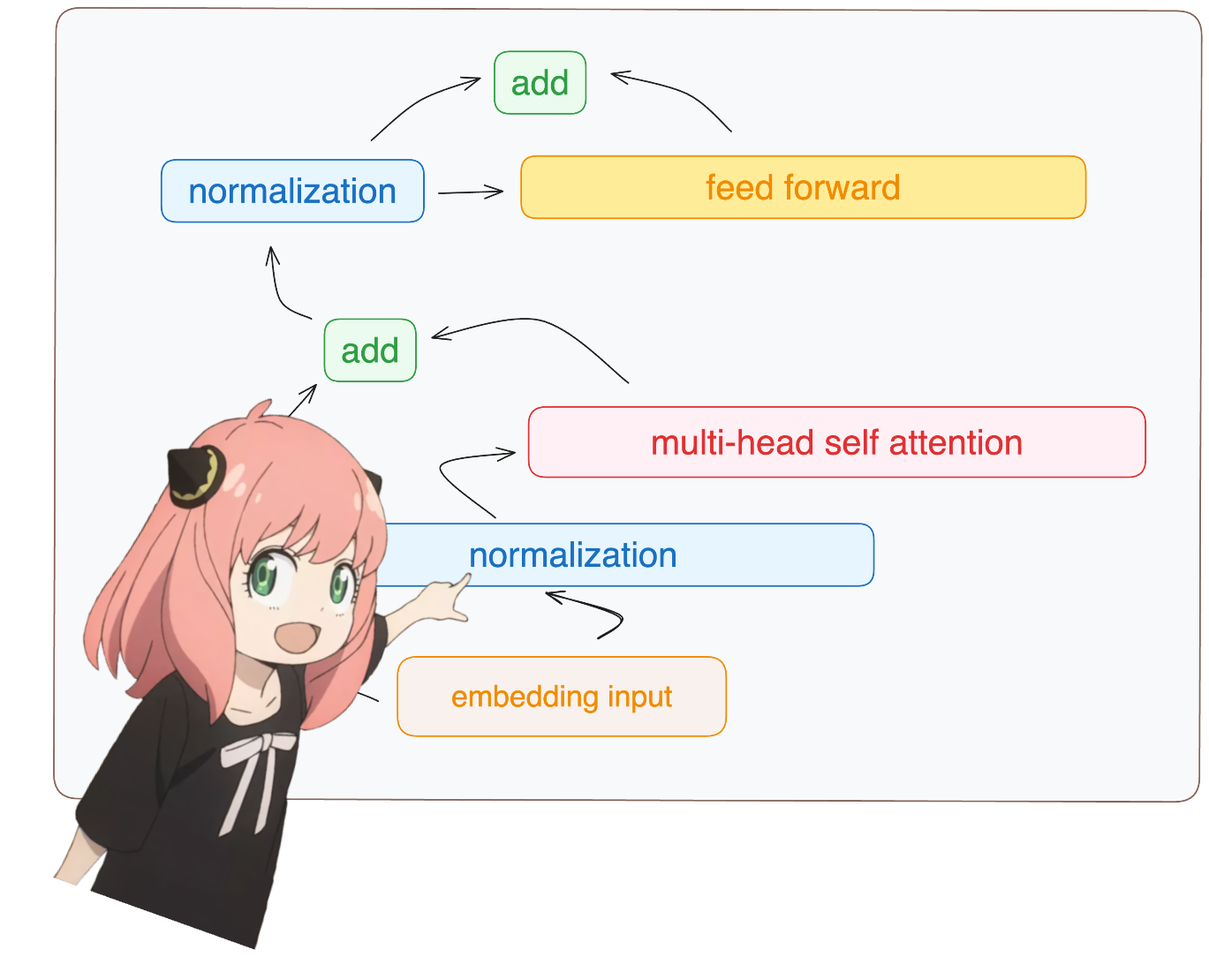
token_embeddings = rms_norm ( token_embeddings_unnormalized , model [ "layers.0.attention_norm.weight" ])
token_embeddings . shape torch.Size([17, 4096])
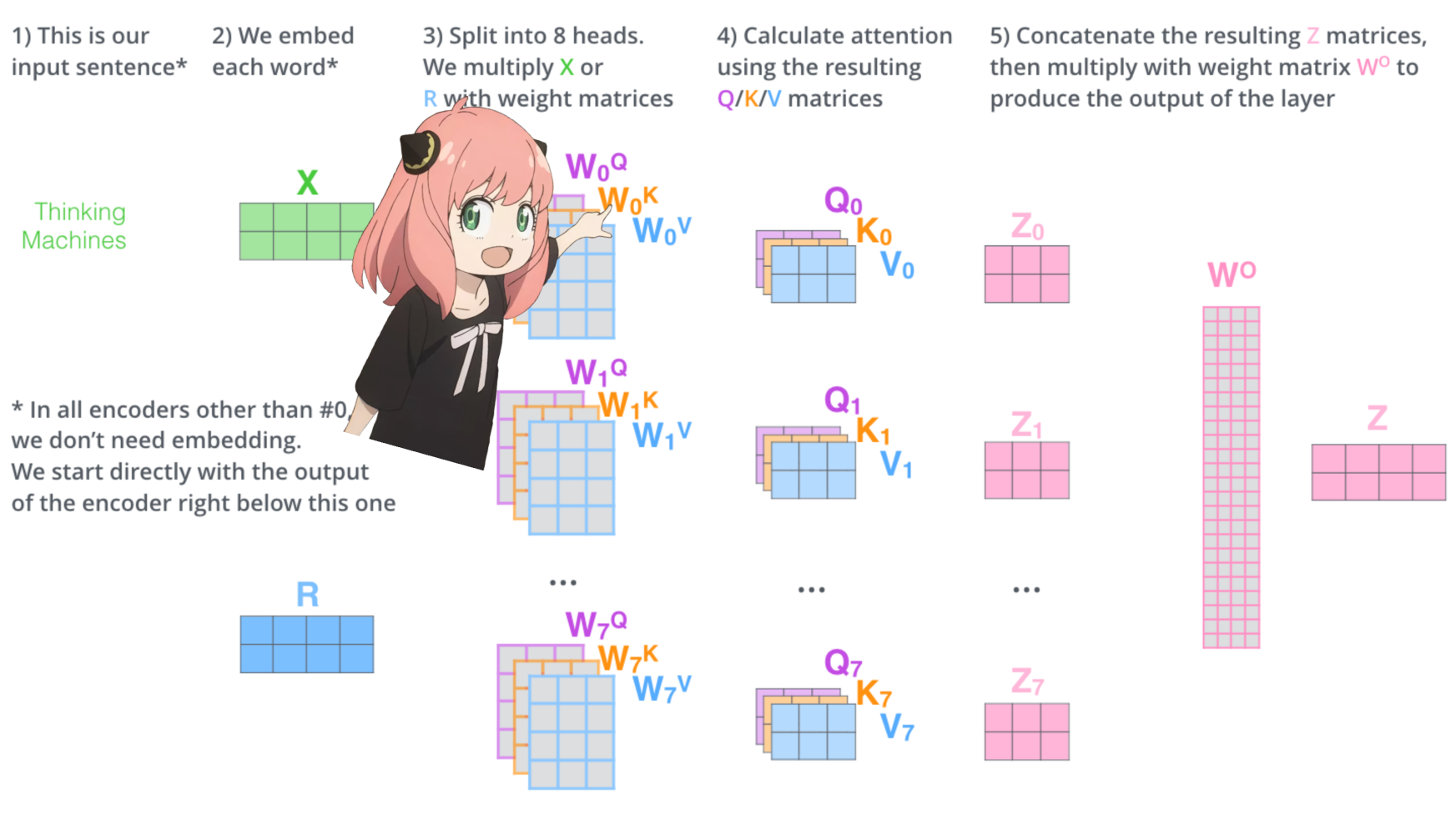
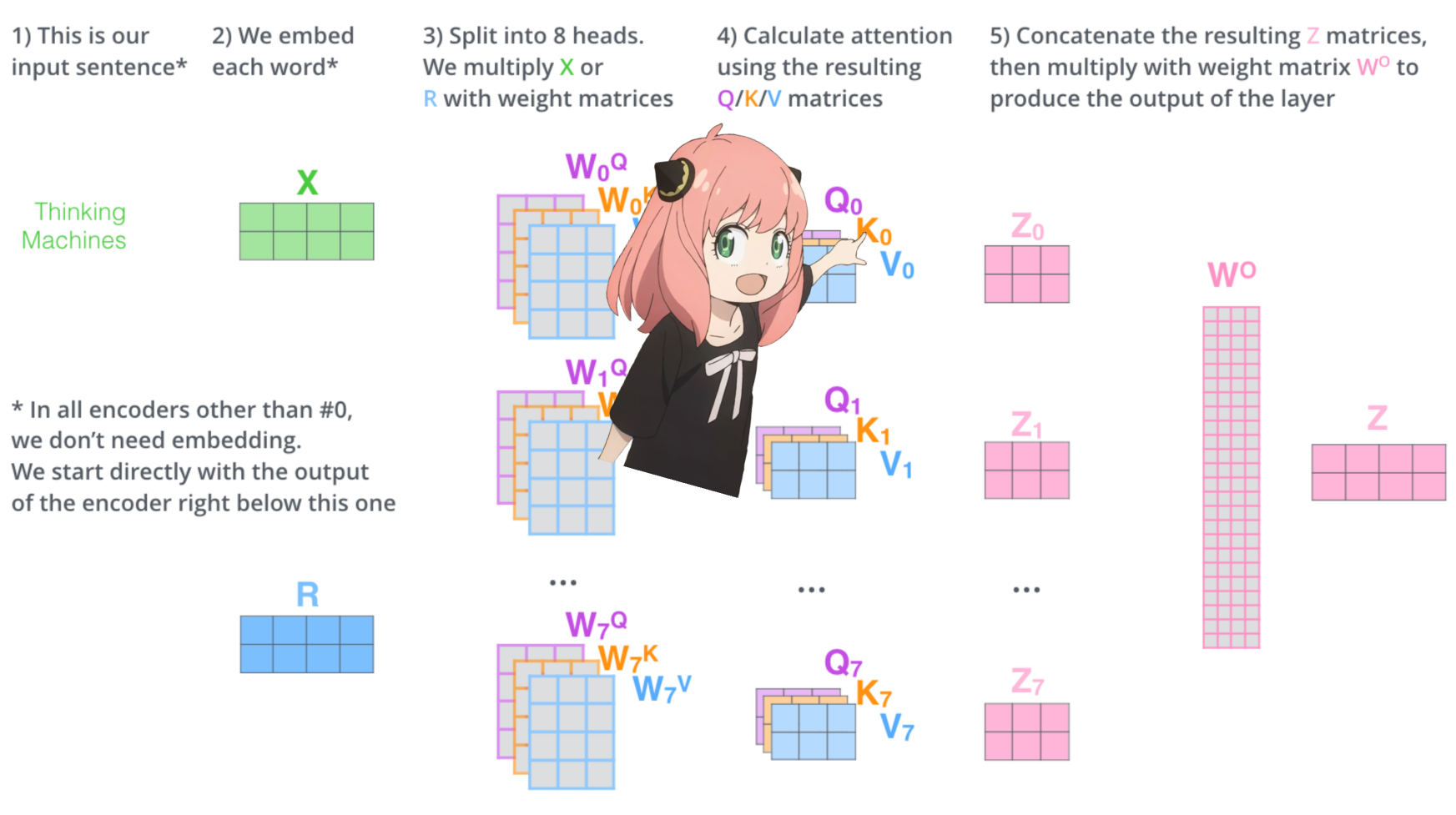
vamos carregar as cabeças de atenção da primeira camada do transformador
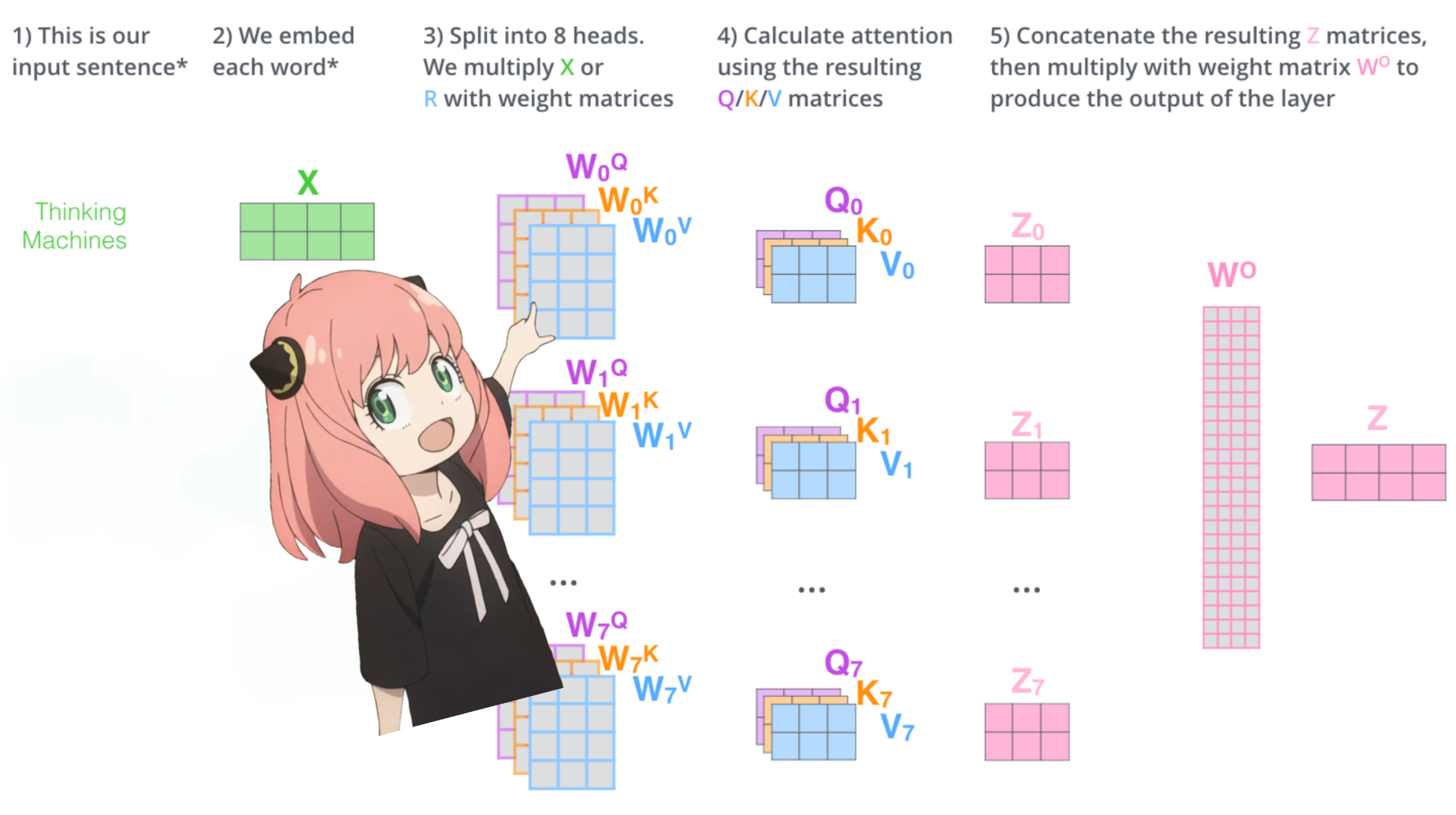
> quando carregamos os vetores de consulta, chave, valor e saída do modelo, notamos que as formas são [4096x4096], [1024x4096], [1024x4096], [4096x4096]
> à primeira vista isso é estranho porque idealmente queremos cada q,k,v e o para cada cabeça individualmente
> os autores do código os agruparam porque é fácil, pois ajuda a paralelizar a multiplicação da cabeça de atenção.
>vou desembrulhar tudo...
print (
model [ "layers.0.attention.wq.weight" ]. shape ,
model [ "layers.0.attention.wk.weight" ]. shape ,
model [ "layers.0.attention.wv.weight" ]. shape ,
model [ "layers.0.attention.wo.weight" ]. shape
) torch.Size([4096, 4096]) torch.Size([1024, 4096]) torch.Size([1024, 4096]) torch.Size([4096, 4096])
na próxima seção, desembrulharemos as consultas de vários cabeçalhos de atenção, a forma resultante é [32x128x4096]
aqui, 32 é o número de cabeças de atenção em llama3, 128 é o tamanho do vetor de consulta e 4096 é o tamanho da incorporação do token
q_layer0 = model [ "layers.0.attention.wq.weight" ]
head_dim = q_layer0 . shape [ 0 ] // n_heads
q_layer0 = q_layer0 . view ( n_heads , head_dim , dim )
q_layer0 . shape torch.Size([32, 128, 4096])
aqui eu acesso a matriz de pesos de consulta primeiro cabeçalho da primeira camada, o tamanho dessa matriz de pesos de consulta é [128x4096]
q_layer0_head0 = q_layer0 [ 0 ]
q_layer0_head0 . shape torch.Size([128, 4096])
aqui você pode ver que a forma resultante é [17x128], isso ocorre porque temos 17 tokens e para cada token há uma consulta de 128 comprimentos.

q_per_token = torch . matmul ( token_embeddings , q_layer0_head0 . T )
q_per_token . shape torch.Size([17, 128])
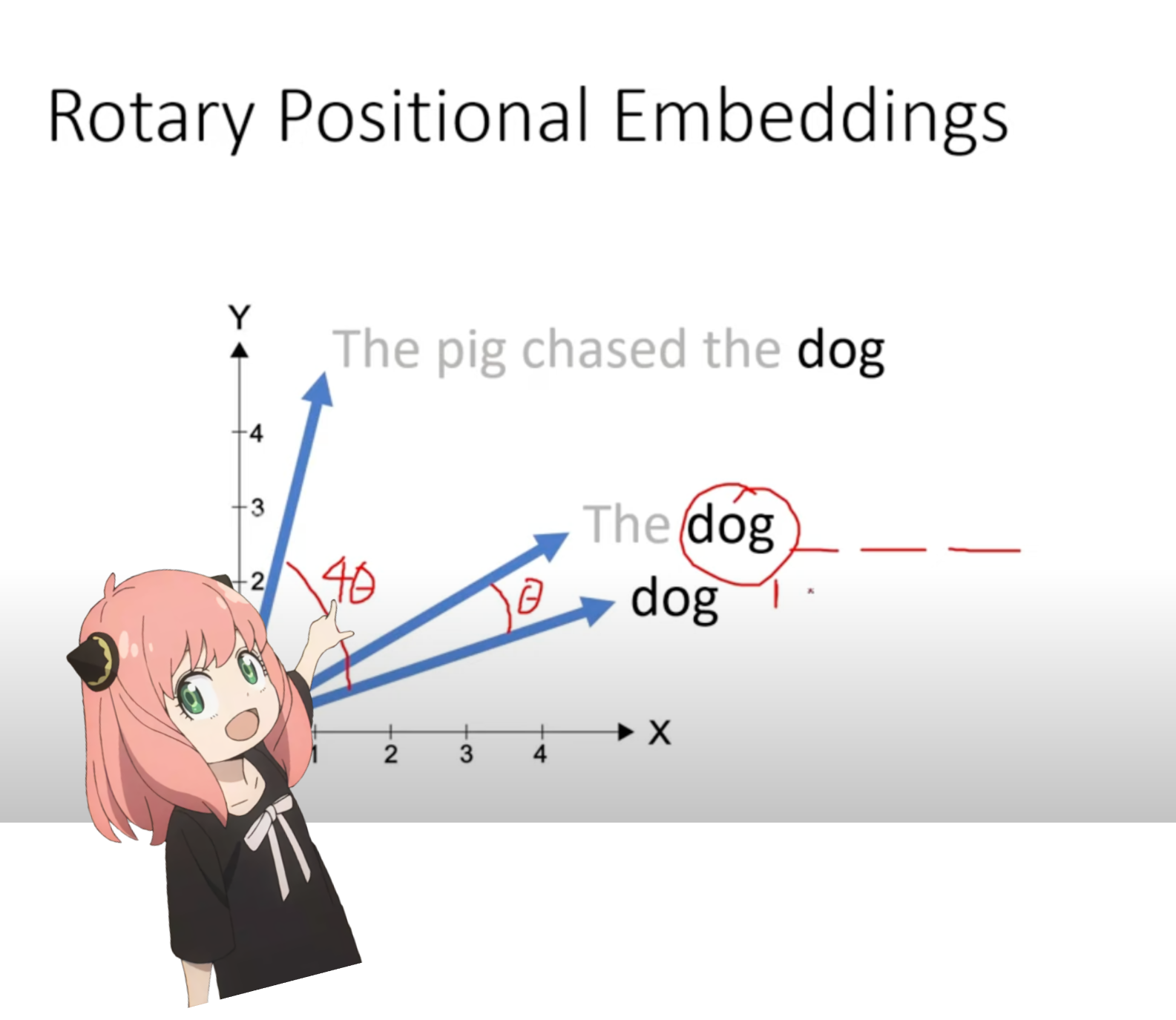
agora estamos em um estágio em que temos um vetor de consulta para cada token em nosso prompt, mas se você pensar bem - o vetor de consulta individual não tem ideia sobre a posição no prompt.
pergunta: "a resposta para a questão final da vida, do universo e de tudo é"
em nosso prompt, usamos "the" três vezes, precisamos que os vetores de consulta de todos os 3 tokens "the" tenham vetores de consulta diferentes (cada um de tamanho [1x128]) com base em suas posições na consulta. realizamos essas rotações usando RoPE (incorporação posicional rotativa).
assista a este vídeo (foi isso que eu assisti) para entender a matemática. https://www.youtube.com/watch?v=o29P0Kpobz0&t=530s
q_per_token_split_into_pairs = q_per_token . float (). view ( q_per_token . shape [ 0 ], - 1 , 2 )
q_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
na etapa acima, dividimos os vetores de consulta em pares, aplicamos uma mudança de ângulo de rotação a cada par!
agora temos um vetor de tamanho [17x64x2], estas são as consultas de 128 comprimentos divididas em 64 pares para cada token no prompt! cada um desses 64 pares será girado por m*(theta) onde m é a posição do token para o qual estamos girando a consulta!

zero_to_one_split_into_64_parts = torch . tensor ( range ( 64 )) / 64
zero_to_one_split_into_64_parts tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250,
0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656,
0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062,
0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469,
0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875,
0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281,
0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688,
0.9844])
freqs = 1.0 / ( rope_theta ** zero_to_one_split_into_64_parts )
freqs tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01,
2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01,
8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02,
2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03,
7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03,
2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04,
6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04,
1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05,
5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05,
1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06,
4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06])
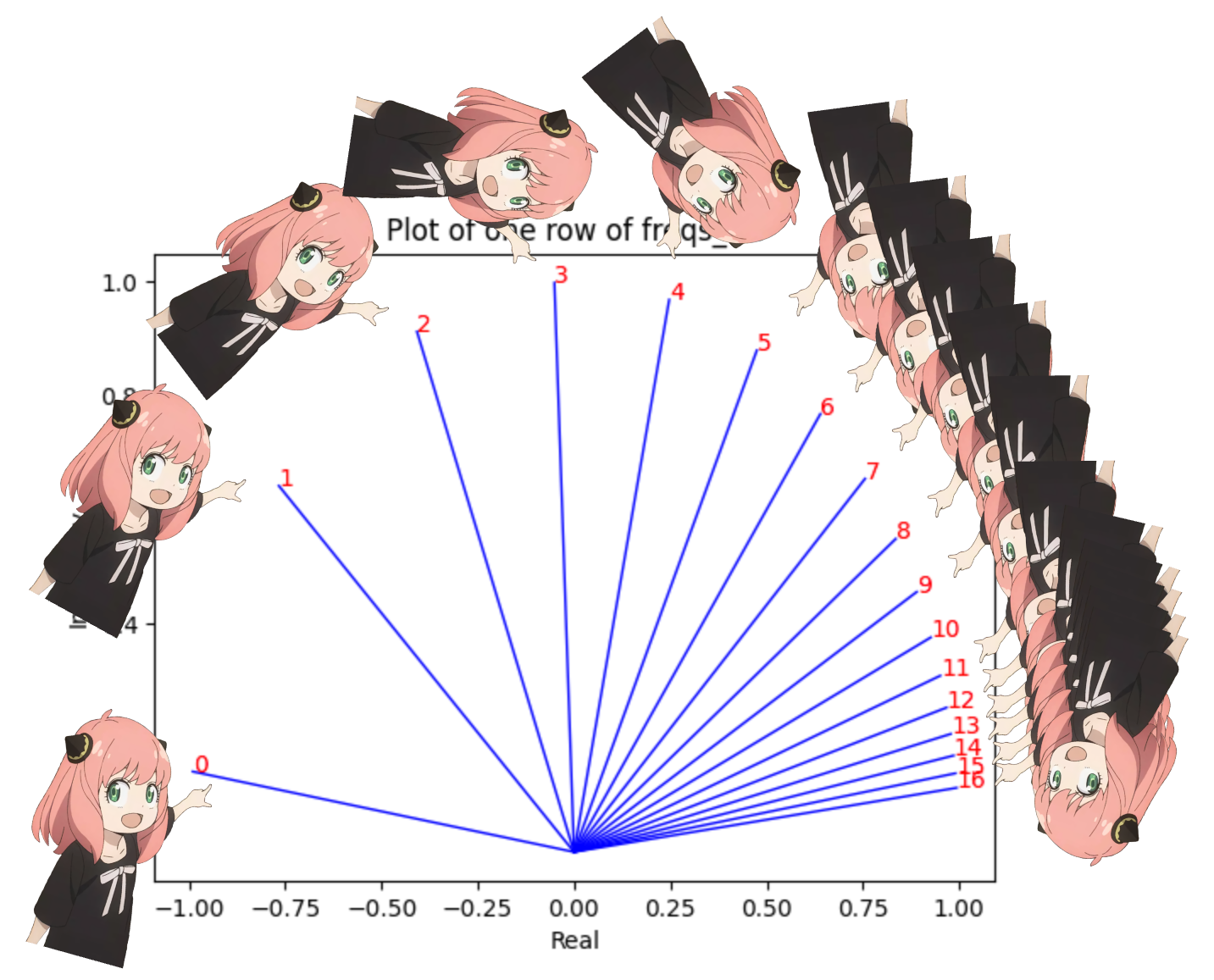
freqs_for_each_token = torch . outer ( torch . arange ( 17 ), freqs )
freqs_cis = torch . polar ( torch . ones_like ( freqs_for_each_token ), freqs_for_each_token )
freqs_cis . shape
# viewing tjhe third row of freqs_cis
value = freqs_cis [ 3 ]
plt . figure ()
for i , element in enumerate ( value [: 17 ]):
plt . plot ([ 0 , element . real ], [ 0 , element . imag ], color = 'blue' , linewidth = 1 , label = f"Index: { i } " )
plt . annotate ( f" { i } " , xy = ( element . real , element . imag ), color = 'red' )
plt . xlabel ( 'Real' )
plt . ylabel ( 'Imaginary' )
plt . title ( 'Plot of one row of freqs_cis' )
plt . show ()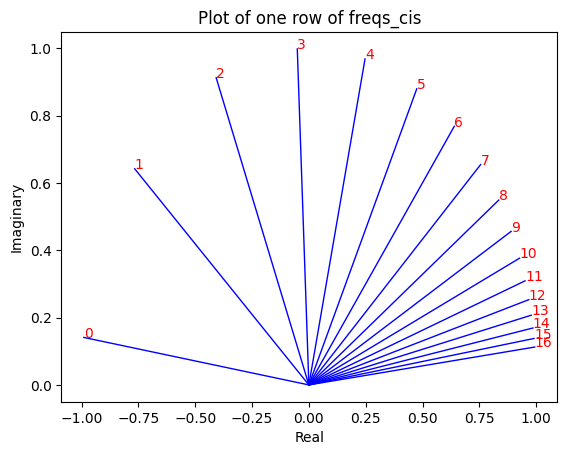
podemos converter nossas consultas (aquela que dividimos em pares) como números complexos e, em seguida, produto escalar para girar a consulta com base na posição
honestamente, é lindo pensar nisso :)
q_per_token_as_complex_numbers = torch . view_as_complex ( q_per_token_split_into_pairs )
q_per_token_as_complex_numbers . shape torch.Size([17, 64])
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cis
q_per_token_as_complex_numbers_rotated . shape torch.Size([17, 64])
podemos recuperar nossas consultas como pares visualizando os números complexos como números reais novamente
q_per_token_split_into_pairs_rotated = torch . view_as_real ( q_per_token_as_complex_numbers_rotated )
q_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
os pares girados agora estão mesclados, agora temos um novo vetor de consulta (vetor de consulta girado) que tem o formato [17x128], onde 17 é o número de tokens e 128 é a dimensão do vetor de consulta
q_per_token_rotated = q_per_token_split_into_pairs_rotated . view ( q_per_token . shape )
q_per_token_rotated . shape torch.Size([17, 128])
k_layer0 = model [ "layers.0.attention.wk.weight" ]
k_layer0 = k_layer0 . view ( n_kv_heads , k_layer0 . shape [ 0 ] // n_kv_heads , dim )
k_layer0 . shape torch.Size([8, 128, 4096])
k_layer0_head0 = k_layer0 [ 0 ]
k_layer0_head0 . shape torch.Size([128, 4096])
k_per_token = torch . matmul ( token_embeddings , k_layer0_head0 . T )
k_per_token . shape torch.Size([17, 128])
k_per_token_split_into_pairs = k_per_token . float (). view ( k_per_token . shape [ 0 ], - 1 , 2 )
k_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
k_per_token_as_complex_numbers = torch . view_as_complex ( k_per_token_split_into_pairs )
k_per_token_as_complex_numbers . shape torch.Size([17, 64])
k_per_token_split_into_pairs_rotated = torch . view_as_real ( k_per_token_as_complex_numbers * freqs_cis )
k_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
k_per_token_rotated = k_per_token_split_into_pairs_rotated . view ( k_per_token . shape )
k_per_token_rotated . shape torch.Size([17, 128])
fazer isso nos dará uma pontuação mapeando cada token entre si
esta pontuação descreve o quão bem a consulta de cada token se relaciona com a chave de cada token. ISSO É AUTOATENÇÃO :)
o formato da matriz de pontuação de atenção (qk_per_token) é [17x17] onde 17 é o número de tokens no prompt
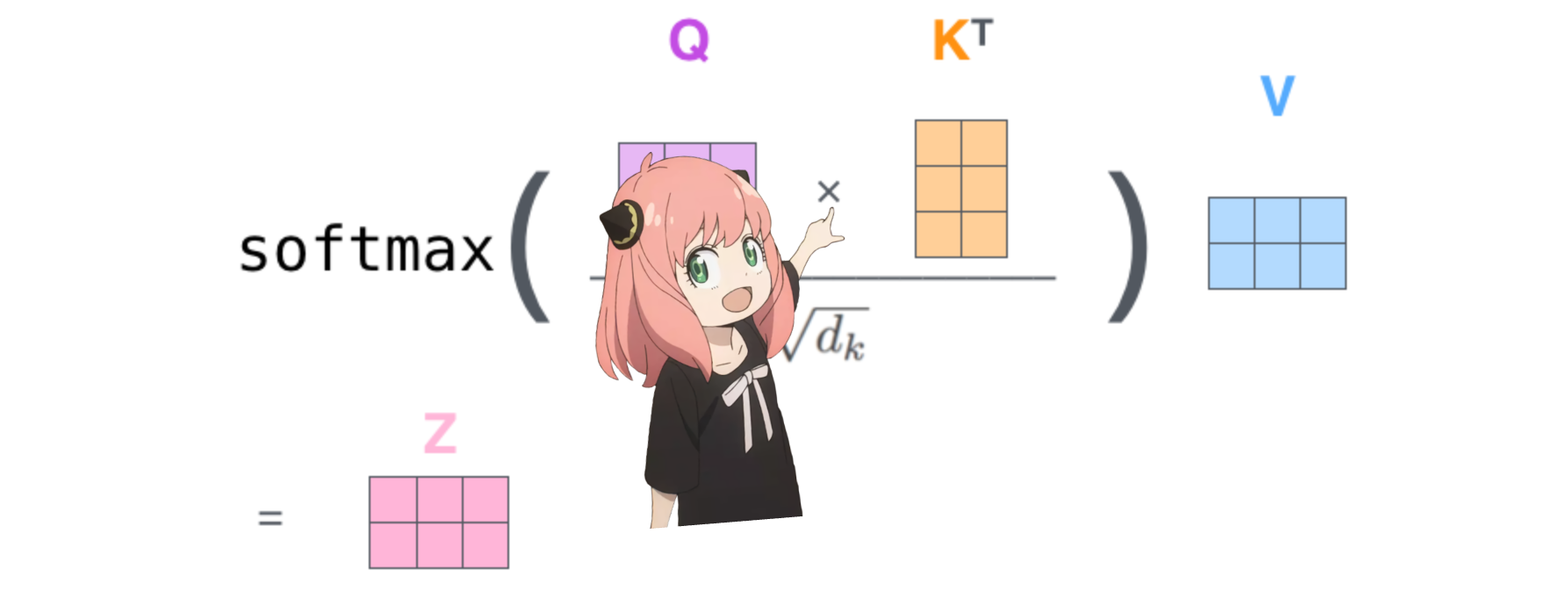
qk_per_token = torch . matmul ( q_per_token_rotated , k_per_token_rotated . T ) / ( head_dim ) ** 0.5
qk_per_token . shape torch.Size([17, 17])
durante o processo de treinamento do llama3, as pontuações futuras do token qk são mascaradas.
por que? porque durante o treinamento só aprendemos a prever tokens usando tokens anteriores.
como resultado, durante a inferência definimos os tokens futuros como zero.
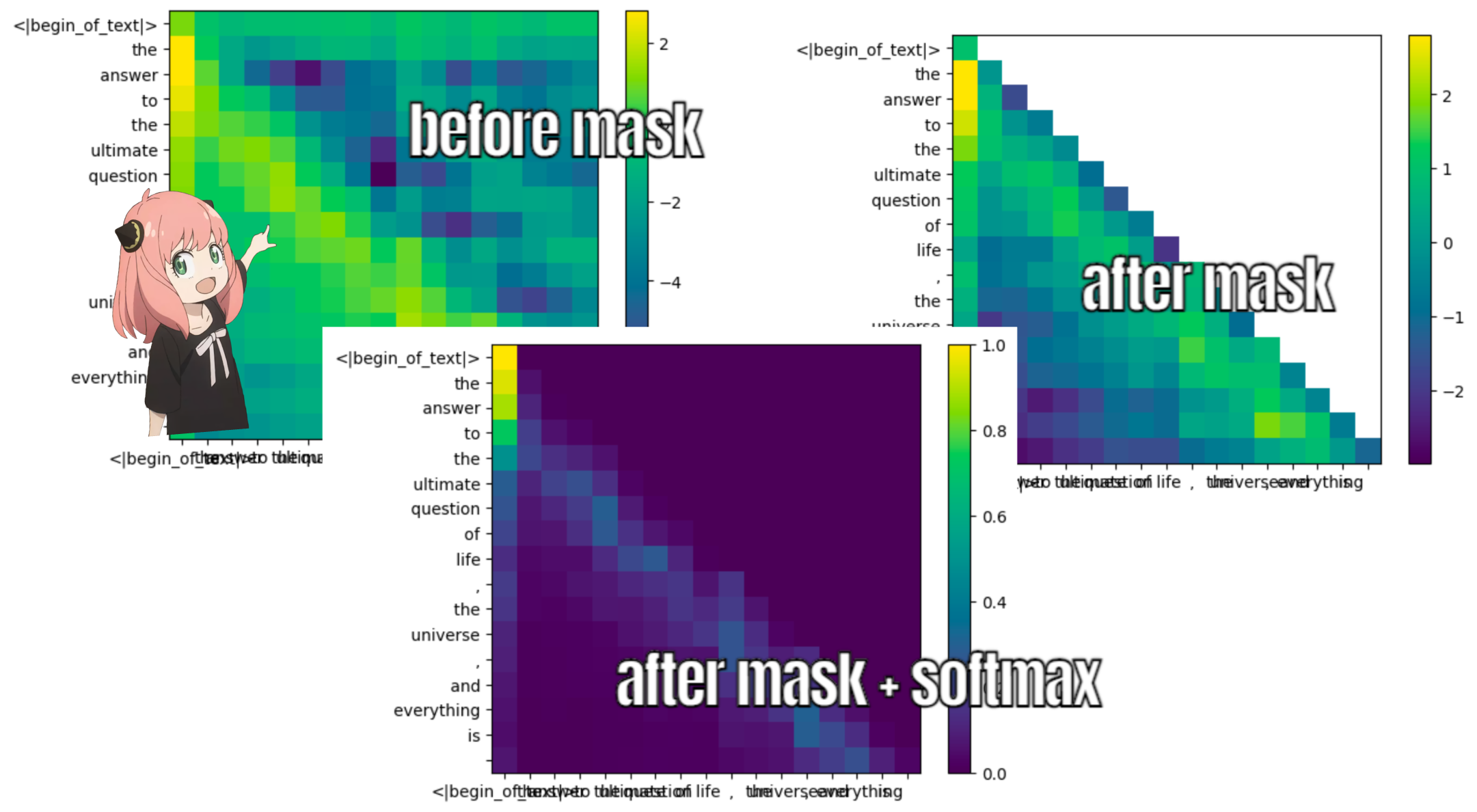
def display_qk_heatmap ( qk_per_token ):
_ , ax = plt . subplots ()
im = ax . imshow ( qk_per_token . to ( float ). detach (), cmap = 'viridis' )
ax . set_xticks ( range ( len ( prompt_split_as_tokens )))
ax . set_yticks ( range ( len ( prompt_split_as_tokens )))
ax . set_xticklabels ( prompt_split_as_tokens )
ax . set_yticklabels ( prompt_split_as_tokens )
ax . figure . colorbar ( im , ax = ax )
display_qk_heatmap ( qk_per_token )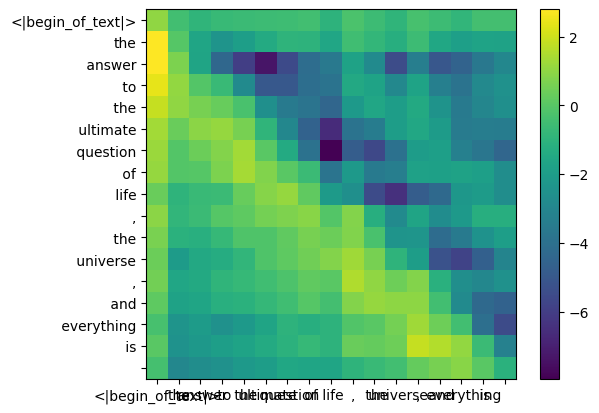
mask = torch . full (( len ( tokens ), len ( tokens )), float ( "-inf" ), device = tokens . device )
mask = torch . triu ( mask , diagonal = 1 )
mask tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
qk_per_token_after_masking = qk_per_token + mask
display_qk_heatmap ( qk_per_token_after_masking )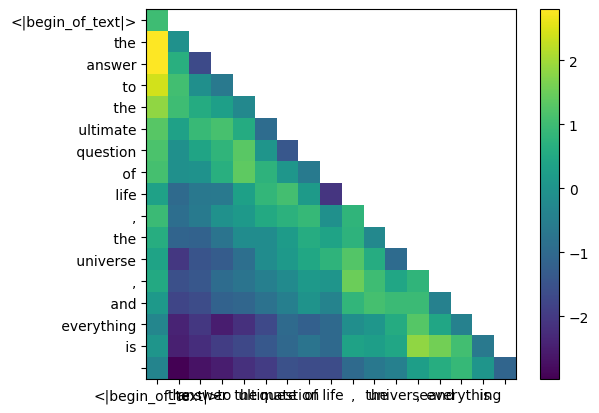
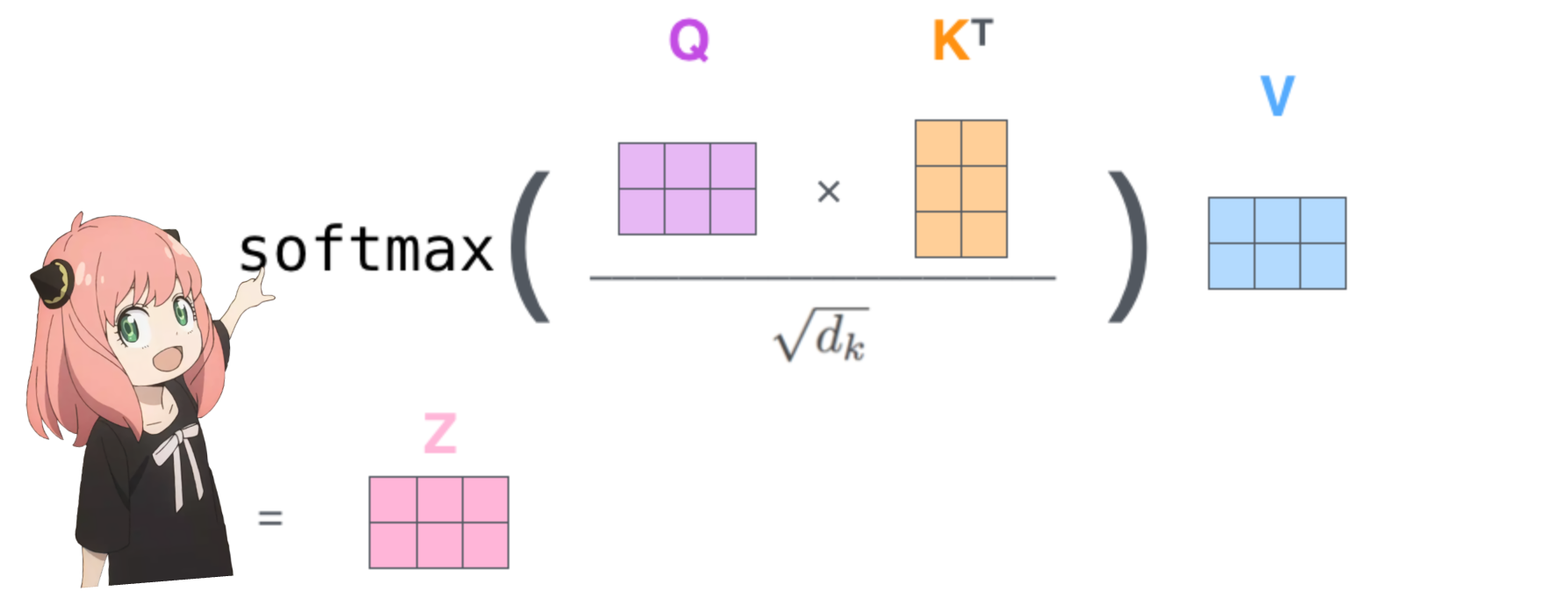
qk_per_token_after_masking_after_softmax = torch . nn . functional . softmax ( qk_per_token_after_masking , dim = 1 ). to ( torch . bfloat16 )
display_qk_heatmap ( qk_per_token_after_masking_after_softmax )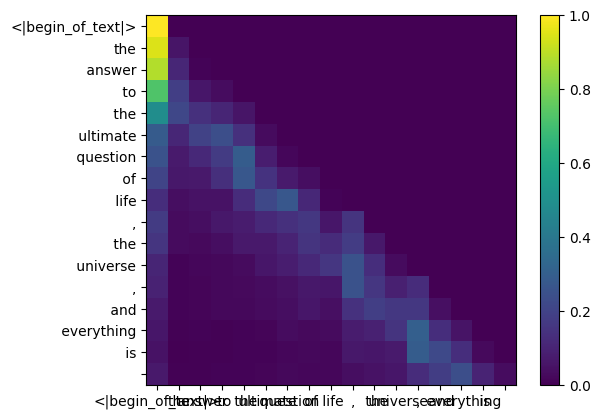
v_layer0 = model [ "layers.0.attention.wv.weight" ]
v_layer0 = v_layer0 . view ( n_kv_heads , v_layer0 . shape [ 0 ] // n_kv_heads , dim )
v_layer0 . shape torch.Size([8, 128, 4096])
a primeira camada, a primeira matriz de peso do valor principal é fornecida abaixo
v_layer0_head0 = v_layer0 [ 0 ]
v_layer0_head0 . shape torch.Size([128, 4096])
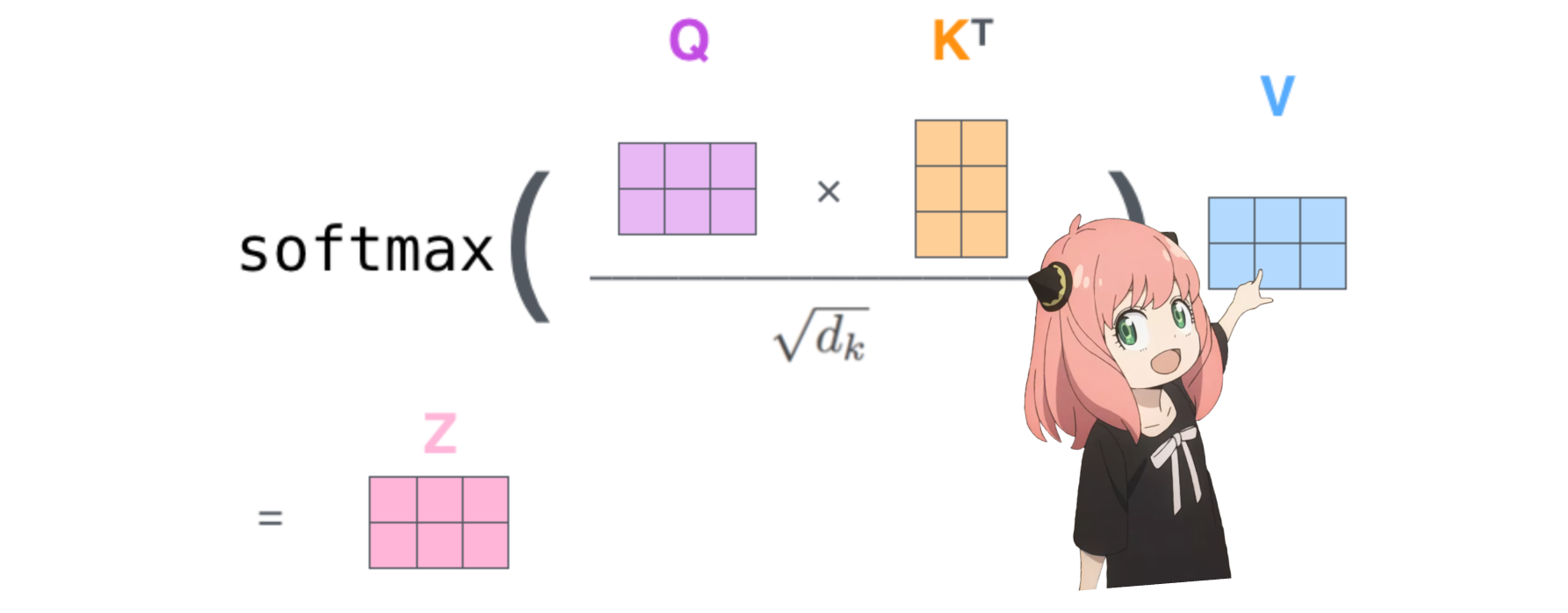
v_per_token = torch . matmul ( token_embeddings , v_layer0_head0 . T )
v_per_token . shape torch.Size([17, 128])
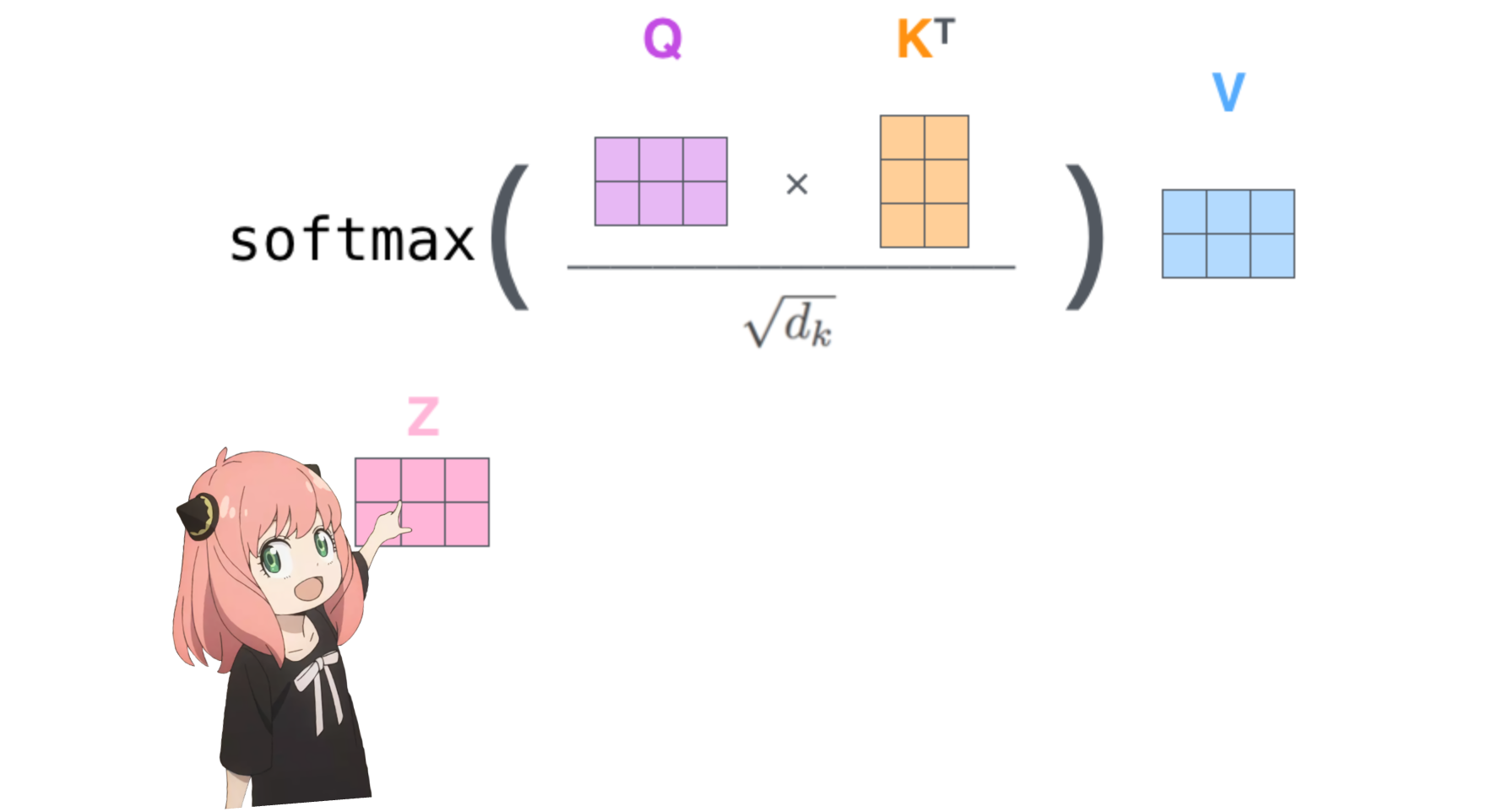
qkv_attention = torch . matmul ( qk_per_token_after_masking_after_softmax , v_per_token )
qkv_attention . shape torch.Size([17, 128])
