greta.gam permite usar funções mais suaves e sintaxe de fórmula do mgcv para definir termos suaves para uso em um modelo greta. Você pode então definir sua própria probabilidade de completar o modelo e ajustá-lo pelo MCMC.
Este é um trabalho em andamento!
Aqui está um exemplo simples adaptado do arquivo de ajuda mgcv ?gam :
Em mgcv :
library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )
# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model
# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat ) Agora ajustando o mesmo modelo em greta :
library( greta.gam )
# > Loading required package: greta
# >
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# >
# > binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# >
# > %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# > eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# > tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!
# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )
# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))
# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )
# build model
m <- model( z_pred )
# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#> warmup 0/1000 | eta: ?s warmup == 50/1000 | eta: 30s warmup ==== 100/1000 | eta: 17s warmup ====== 150/1000 | eta: 12s warmup ======== 200/1000 | eta: 10s warmup ========== 250/1000 | eta: 8s warmup =========== 300/1000 | eta: 7s warmup ============= 350/1000 | eta: 6s warmup =============== 400/1000 | eta: 5s warmup ================= 450/1000 | eta: 5s warmup =================== 500/1000 | eta: 4s warmup ===================== 550/1000 | eta: 4s warmup ======================= 600/1000 | eta: 3s warmup ========================= 650/1000 | eta: 3s warmup =========================== 700/1000 | eta: 2s warmup ============================ 750/1000 | eta: 2s warmup ============================== 800/1000 | eta: 1s warmup ================================ 850/1000 | eta: 1s warmup ================================== 900/1000 | eta: 1s warmup ==================================== 950/1000 | eta: 0s warmup ====================================== 1000/1000 | eta: 0s
# > sampling 0/200 | eta: ?s sampling ========== 50/200 | eta: 1s sampling =================== 100/200 | eta: 0s sampling ============================ 150/200 | eta: 0s sampling ====================================== 200/200 | eta: 0s
# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])
# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL
# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )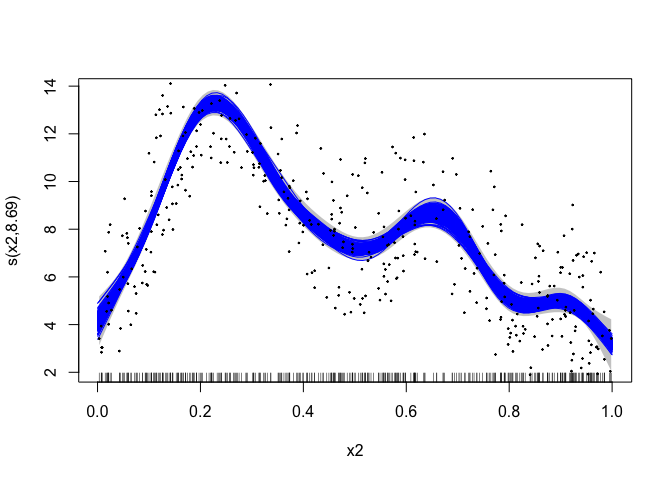
greta.gam usa alguns truques da rotina jagam (Wood, 2016) no mgcv para fazer as coisas funcionarem. Aqui estão alguns breves detalhes para os interessados no funcionamento interno…
GAMs são modelos com interpretações bayesianas (mesmo quando ajustados por métodos “frequentistas”). Pode-se pensar na matriz de penalidade mais suave como uma matriz de precisão anterior em um modelo Bayesiano de efeitos aleatórios. As matrizes de projeto são construídas exatamente como no caso frequentista. Veja Miller (2021) para mais informações sobre isso.
Há uma ligeira dificuldade na interpretação bayesiana do GAM, pois, em sua forma ingênua, os anteriores são impróprios como espaço nulo da penalidade (no caso 1D, geralmente o termo linear). Para obter antecedentes adequados podemos usar um dos “truques” empregados em Marra & Wood (2011) – que é penalizar de alguma forma as partes da penalidade que levam ao prior impróprio. Tomamos a opção fornecida por jagam e criamos uma matriz de penalidade adicional para esses termos (a partir de uma decomposição própria da matriz de penalidade; ver Marra & Wood, 2011).
Marra, G e Wood, SN (2011) Seleção prática de variáveis para modelos aditivos generalizados. Estatística Computacional e Análise de Dados, 55, 2372–2387.
Miller DL (2021). Visões bayesianas de modelagem aditiva generalizada. arXiv.
Wood, SN (2016) Apenas outro modelador aditivo Gibbs: interfaceando JAGS e mgcv. Journal of Statistical Software 75, não. 7