practico 1 series

Visual Básico

1.0.0

Baixar

Prática 1 - Série

Série prática de introdução à computação com o engenheiro Mollo.

Linguagem de programação: Visual Basic
veja PDF da prática

Contente

Gere a tabuada de multiplicação de n
Gere a divisão de n
Gere a soma de n
Gere a subtração de n
Exercício 5
Exercício 6
Exercício 7
Exercício 8
Exercício 9
Exercício 10
Exercício 11
Exercício 12
Exercício 13
Exercício 14
Exercício 15

Exercício 1, 2, 3 e 4

exercício-1-2-3-4

Exercícios 1,2,3,4. Gere a tabela de operações aritméticas de n... termos:

adição
subtração
multiplicação
divisão

Ver código

 Public Function SelectTable(n As Double , operatorString As String ) As String
  Dim result, symbol As String
  Dim index As Integer
  Dim res As Double
  result = "" : symbol = ""
  For index = 0 To 10
      Select Case operatorString
          Case "*"
              symbol = " *"
              res = (index * n)
          Case "/"
              symbol = " /"
              res = (index / n)
          Case "+"
              symbol = " +"
              res = (index + n)
          Case "-"
              symbol = " -"
              res = (index - n)
      End Select
      result = result + Str(index) + symbol + Str(n) + " = " + Str(res) + Chr( 13 ) + Chr( 10 )
  Next
  Return result
End Function

 # Output: SelectTable(TextBox1.Text, "+")
 0 + 5 =  5
 1 + 5 =  6
 2 + 5 =  7
 3 + 5 =  8
 4 + 5 =  9
 5 + 5 =  10
 6 + 5 =  11
 7 + 5 =  12
 8 + 5 =  13
 9 + 5 =  14
 10 + 5 =  15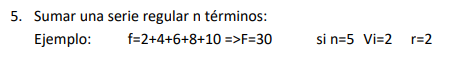

Exercício 5

exercício-5

Adicione uma série regular de n termos:

Ver código

 Public Function RegularSerie(n As UInt16, initialValue As Single , razon As Single , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As UInt32
    Dim t, total As Single
    For index = 1 To n
        t = initialValue + (index - 1 ) * razon
        If sumTotal Then
            total += t
            result = Str(total)
        Else
            If index = n Then
                result += Str(t)
            Else
                result = result + Str(t) + "  + "
            End If
        End If
    Next
    Return "F = " + result
End Function

 # Output: RegularSerie(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 30
# Output string: RegularSerie(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F =  2  +  4  +  6  +  8  +  10

Exercício 6

exercício-6

F = (ln(10)+1)/1.7 + (ln(100)+2)/1.9... O argumento Log10 está se multiplicando. X10, X10,..use acumulador multiplicador.

Ver código

 Public Function LogarithmSerie(n As Integer , initialValue As Double , razon As Double , arg As Double , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim count As Double
    Dim index As Integer
    Dim t, f, total As Double
    count = arg
    t = initialValue
    For index = 1 To n
        If sumTotal Then
            f = (Math.Log10(count) + index) / t
            total += f
            result = Str(total)
        Else
            If index.Equals(n) Then
                result = result + "(ln(" + Str(count) + ")+" + Str(index) + ")/" + Str(t)
            Else
                result = result + "(ln(" + Str(count) + ")+" + Str(index) + ")/" + Str(t) + "+  "
            End If
        End If
        count *= 10
        t = Math.Round(t + razon, 2 )
    Next
    Return "F = " + result
End Function

 # Output: LogarithmSerie(TextBox1.Text, vi, r, arg, True)
F = 13.617137472838102
# Output string: LogarithmSerie(TextBox1.Text, vi, r, arg, False)
F = (ln(10)+1)/1.7 +  (ln(100)+ 2)/ 1.9  +  (ln(1000)+3)/2.1  + (ln(10000)+4)/2.3  +  (ln(100000)+5)/2.5

Exercício 7

exercício-7

F = 100/1 + 99/2 + 97/4... o numerador reduz o termo em 1, 2, 3... enquanto o denominador aumenta em 1,2,3..., deve ter o valor inicial do numerador VIN= 100, e valor inicial do denominador VID=1.

Ver código

 Public Function IncreaseAndDecrease(n As Integer , initialValueNumerator As Integer , initialValueDenominator As Integer , isSumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim f, total As Double
    For index = 1 To n
        If isSumTotal Then
            f = (initialValueNumerator / initialValueDenominator)
            total += f
            result = Str(total)
        Else
            If index = n Then
                result = result + Str(initialValueNumerator) + "/" + Str(initialValueDenominator)
            Else
                result = result + Str(initialValueNumerator) + "/" + Str(initialValueDenominator) + " +  "
            End If
        End If
        initialValueNumerator -= index
        initialValueDenominator += index
    Next
    Return "F =" + result
End Function

 # Output: IncreaseAndDecrease(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 195.3603896103896
# Output string: IncreaseAndDecrease(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 100/ 1 +   99/ 2 +   97/ 4 +   94/ 7 +   90/ 11

Exercício 8

exercício-8

F = 5.25/0!+0 + 5.24/1!+1 + 5.22/2!+2... Ambos os elementos são séries regulares e para o denominador você só precisa chamar a função fatorial, claro que você deve aprender a fazer o algoritmo para o exame.

Ver código

 Public Function Factorial(number As Double ) As Double
    Dim fac As Double
    Dim index As Integer
    If number <> 0 Then
        fac = 1
        For index = Math.Abs(number) To 1 Step - 1
            fac *= index
        Next
        If number < 0 Then
            fac = -fac
        End If
    Else
        fac = 1
    End If
    Return fac
End Function
Public Function RegularSerieWithFactorial(n As Integer , initialValueNum As Double , initialValueDen As Double , sumTotal As Double ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim t, f, total As Double
    For index = 0 To n
        If sumTotal Then
            If initialValueDen = 0 Then
                f = 0
            Else
                f = initialValueNum / (Factorial(initialValueDen) + initialValueDen)
            End If
            total += f
            result = Str(total)
        Else
            t = index + 1
            If index = n Then
                result = result + Str(Math.Round(initialValueNum, 2 )) + "/(!" + Str(initialValueDen) + "+" + Str(initialValueDen) + ")"
            Else
                result = result + Str(Math.Round(initialValueNum, 2 )) + "/(!" + Str(initialValueDen) + "+" + Str(initialValueDen) + ")  +  "
            End If
        End If
        initialValueNum -= (t / 100 )
        initialValueDen += 1
    Next
    Return "F = " + result
End Function

 # Output: RegularSerieWithFactorial(TextBox1.Text, vi, r, True)
F = 4.750333333333333
# Output string: RegularSerieWithFactorial(TextBox1.Text, vi, r, False)
F = 5.25/( ! 0+0) + 5.24/( ! 1+1) + 5.22/( ! 2+2) + 5.19/( ! 3+3) + 5.15/( ! 4+4) + 5.1/( ! 5+5)

Exercício 9

exercício-9

F = X^2/2! + X^4/4! + X^6/6!+… X, é apenas uma variável de entrada que deve ser considerada no termo

Ver código

 Public Function SumFactorial(n As Integer , x As Single , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim formule As Double
    If n = 0 Then
        result = Str( 0 )
    End If
    For index = 1 To n
        If sumTotal Then
            formule = Math.Pow(x, index * 2 ) / Factorial(index * 2 )
            result = Str(formule)
        Else
            If index = n Then
                result = result + "(" + Str(x) + "^" + Str(index * 2 ) + ")/" + Str(index * 2 ) + "!"
            Else
                result = result + "(" + Str(x) + "^" + Str(index * 2 ) + ")/" + Str(index * 2 ) + "! + "
            End If
        End If
    Next
    Return "F = " + result
End Function

 # Output: SumFactorial(TextBox1.Text, TextBox2.Text, True)
F = 0.0002821869488536155
# Output string: SumFactorial(TextBox1.Text, TextBox2.Text, False)
F = (2^2)/ 2 ! + (2^4)/ 4 ! + (2^6)/ 6 ! + (2^8)/ 8 ! + (2^10)/ 10 !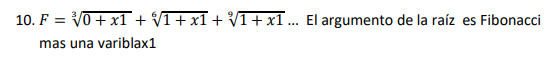

Exercício 10

exercício-10

3√(0+x1) + 6√(1+x1) + 9√(1+x1)... O argumento raiz é Fibonacci mais uma variável x1.

Ver código

 Public Function SerieProgresiveFibonacci(n As Integer , x As Double , viRoot As Integer , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index, a, b, c, root As Integer
    Dim formule, total As Double
    a = - 1 : b = 1 : root = viRoot
    For index = 1 To n
        c = a + b
        If sumTotal Then
            formule = (c + x) ^ ( 1 / root)
            total += formule
            result = Str(total)
        Else
            If index = n Then
                result = result + Str(index * 3 ) + "√(" + Str(c) + "+" + Str(x) + ")"
            Else
                result = result + Str(index * 3 ) + "√(" + Str(c) + "+" + Str(x) + ") + "
            End If
        End If
        a = b
        b = c
        root *= 3
    Next
    Return "F = " + result
End Function

 # Output: SerieProgresiveFibonacci(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 5.455187736786854
# Output string: SerieProgresiveFibonacci(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 3√(0+2) +  6√(1+2) +  9√(1+2) +  12√(2+2) +  15√(3+2)

Exercício 11

exercício-11

20√cos(0.2) - 19√cos(0.4) + 18√cos(0.6)... “pimponea”, ou seja, somar o termo e subtrair, somar e subtrair. ISTO NÃO SÃO N TERMOS, MAS ATÉ A RAIZ SER 2, ENTÃO O ÚLTIMO ELEMENTO SERÁ 2√cos(...).

Ver código

0 Then formule = -Math.Pow(Math.Cos(count), 1 / index) Else formule = Math.Pow(Math.Cos(count), 1 / index) End If total += formule result = Str(total) Else If index = 2 Then result = result + Str(index) + "√cos(" + Str(count) + ")" Else If index Mod 2 <> 0 Then result = result + Str(index) + "√cos(" + Str(count) + ") + " Else result = result + Str(index) + "√cos(" + Str(count) + ") - " End If End If End If count = Math.Round(count + razon, 2) Next Return "F = " + result End Function">

 Public Shared Function Pinponear(root As Double , vi As Double , razon As Double , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim count, total, formule As Double
    count = vi
    For index = root To 2 Step - 1
        If sumTotal Then
            If index Mod 2 <> 0 Then
                formule = -Math.Pow(Math.Cos(count), 1 / index)
            Else
                formule = Math.Pow(Math.Cos(count), 1 / index)
            End If
            total += formule
            result = Str(total)
        Else
            If index = 2 Then
                result = result + Str(index) + "√cos(" + Str(count) + ")"
            Else
                If index Mod 2 <> 0 Then
                    result = result + Str(index) + "√cos(" + Str(count) + ")  + "
                Else
                    result = result + Str(index) + "√cos(" + Str(count) + ")  - "
                End If
            End If
        End If
        count = Math.Round(count + razon, 2 )
    Next
    Return "F = " + result
End Function

 # Output: Pinponear(TextBox1.Text, vi, r, True)
F = 5.455187736786854
# Output string: Pinponear(TextBox1.Text, vi, r, False)
F = 3√(0+2) +  6√(1+2) +  9√(1+2) +  12√(2+2) +  15√(3+2)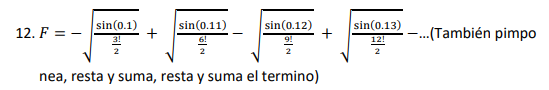

Exercício 12

exercício-12

√(sin(0.1)/(3!/2)) + √(sin(0.11)/(3!/2))... Ele também faz ping, subtrai e adiciona, subtrai e adiciona o termo.

Ver código

 Public Function ProgresiveSeriePinponear(n As Integer , initValue As Double , r As Double , arg As Double , sumTotal As Boolean )
    Dim result As String = ""
    Dim index As Integer
    Dim total, formule, count As Double
    count = initValue
    For index = 1 To n
        If sumTotal Then
            formule = Math.Sqrt(Math.Sin(arg) / (Factorial(count) / 2 ))
            total = -total + formule
            result = Str(total)
        Else
            If index Mod 2 = 0 Then
                result = result + "+ √sin(" + Str(arg) + ")/(" + Str(count) + "!/2) "
            Else
                result = result + "- √sin(" + Str(arg) + ")/(" + Str(count) + "!/2) "
            End If
        End If
        arg = Math.Round(arg + r, 2 )
        count += 3
    Next
    Return "F = " + result
End Function

 # Output: ProgresiveSeriePinponear(TextBox1.Text, vi, r, arg, True)
F = -0.16574853902978934
# Output string: ProgresiveSeriePinponear(TextBox1.Text, vi, r, arg, False)
F = - √sin( 0.1)/( 3 ! /2) + √sin( 0.11)/( 6 ! /2) - √sin( 0.12)/( 9 ! /2) + √sin( 0.13)/( 12 ! /2)

Exercício 13

exercício-13

(π/2)/√(1000+0) + (π/1.9)/√(1001+1) + (π/1.8)/√(1003+1) O argumento da raiz aumenta em uma progressão: Do 1º para o 2º 1; do 2º ao 3º 2; do 3º ao 4º 3; …enquanto o outro é Fibonacci.

Ver código

 Public Function ProgresiveSerieFibonacci(n As Integer , initValue As Integer , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim count, a, b, c, total, formule As Double
    count = 2 : a = - 1 : b = 1
    For index = 1 To n
        c = a + b
        If sumTotal Then
            formule = ( 3.14159 / count) / Math.Sqrt(initValue + c)
            total += formule
            result = Str(total)
        Else
            If index = n Then
                result = result + "(π/" + Str(count) + ")/√(" + Str(initValue) + "+" + Str(c) + ")"
            Else
                result = result + "(π/" + Str(count) + ")/√(" + Str(initValue) + "+" + Str(c) + ")  +  "
            End If
        End If
        a = b
        b = c
        count = Math.Round(count - 0.1 , 2 )
        initValue += index
    Next
    Return "F = " + result
End Function

 # Output: ProgresiveSerieFibonacci(TextBox1.Text, TextBox2.Text, True)
F = 0.27688777750129406
# Output string: ProgresiveSerieFibonacci(TextBox1.Text, TextBox2.Text, False)
F = (π/ 2)/√( 1000+ 0)  +  (π/ 1.9)/√( 1001+ 1)  +  (π/ 1.8)/√( 1003+ 1)  +  (π/ 1.7)/√( 1006+ 2)  +  (π/ 1.6)/√( 1010+ 3)

Exercício 14

exercício-14

2√x^2/100 + 4√x^4/50 + 8√x^8/25... A raiz se multiplica, enquanto o denominador dentro da raiz se desdobra (divide).

Ver código

 Public Function SerieMultiplyAndUnfold(n As Integer , root As Double , num As Double , denom As Double , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim total, formule As Double
    For index = 1 To n
        If sumTotal Then
            formule = Math.Pow(Math.Pow(num, root) / denom, 1 / root)
            total += formule
            result = Str(total)
        Else
            If index = n Then
                result = result + Str(root) + "√(" + Str(num) + "^" + Str(root) + "/" + Str(denom) + ")"
            Else
                result = result + Str(root) + "√(" + Str(num) + "^" + Str(root) + "/" + Str(denom) + ")  +  "
            End If
        End If
        root = Math.Round(root * 2 , 2 )
        denom = Math.Round(denom / 2 , 2 )
    Next
    Return "F = " + result
End Function

 # Output: SerieMultiplyAndUnfold(TextBox1.Text, TextBox2.Text,TextBox3.Text, TextBox4.Text, True)
F = 1.9987716171427177
# Output string with params: SerieMultiplyAndUnfold(4, 2, 1, 100, False)
F = 2√( 1^ 2/ 100)  +   4√( 1^ 4/ 50)  +   8√( 1^ 8/ 25)  +   16√( 1^ 16/ 12.5)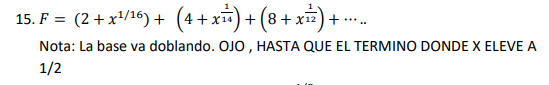

Exercício 15

exercício-15

( 2+x^(1/16)) + (4+x^(1/14))... A base está duplicando. TENHA CUIDADO, ATÉ O PRAZO ONDE X AUMENTA PARA 1/2

Ver código

= 2 Then If index = n Then result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))" Else result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + ")) + " End If End If End If base *= 2 denom -= 2 Next Return "F = " + result End Function">

 Public Function SerieBaseIsDoubling(n As Integer , base As Double , x As Double , denom As Double , sumTotal As Boolean ) As String
    Dim result As String = ""
    Dim index As Integer
    Dim total, formule As Double
    For index = 1 To n
        If sumTotal Then
            formule = base + Math.Pow(x, 1 / denom)
            total += formule
            result = total
        Else
            If denom >= 2 Then
                If index = n Then
                    result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))"
                Else
                    result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))  + "
                End If
            End If
        End If
        base *= 2
        denom -= 2
    Next
    Return "F = " + result
End Function

 # Output: SerieBaseIsDoubling(TextBox1.Text, vi, r, arg, True)
F = 2056
# Output string with params: SerieBaseIsDoubling(10, 2, 1, 16, False)
F = ( 2+ 1^(1/ 16))  + ( 4+ 1^(1/ 14))  + ( 8+ 1^(1/ 12))  + ( 16+ 1^(1/ 10))  + ( 32+ 1^(1/ 8))  + ( 64+ 1^(1/ 6))  + ( 128+ 1^(1/ 4))  + ( 256+ 1^(1/ 2))

Expandir

Informações adicionais