Detecção de valores discrepantes em Python (PyOD)
Implantação e documentação e estatísticas e licença

Leia-me primeiro
Bem-vindo ao PyOD, uma biblioteca Python abrangente, mas fácil de usar, para detectar anomalias em dados multivariados. Esteja você lidando com um projeto de pequena escala ou grandes conjuntos de dados, o PyOD oferece uma variedade de algoritmos para atender às suas necessidades.
- Para detecção de valores discrepantes de série temporal , use TODS.
- Para detecção de valores discrepantes em gráficos , use PyGOD.
- Comparação de desempenho e conjuntos de dados : Temos um documento de referência abrangente de detecção de anomalias de 45 páginas. O ADBench de código aberto compara 30 algoritmos de detecção de anomalias em 57 conjuntos de dados de benchmark.
- Saiba mais sobre detecção de anomalias em Recursos de detecção de anomalias
- PyOD em sistemas distribuídos : você também pode executar PyOD em databricks.
Sobre PyOD
PyOD, estabelecido em 2017, tornou-se uma biblioteca Python indispensável para detectar objetos anômalos/periféricos em dados multivariados. Este campo emocionante, porém desafiador, é comumente conhecido como Detecção de Outliers ou Detecção de Anomalias.
PyOD inclui mais de 50 algoritmos de detecção, desde LOF clássico (SIGMOD 2000) até ECOD e DIF de última geração (TKDE 2022 e 2023). Desde 2017, o PyOD tem sido usado com sucesso em vários projetos de pesquisa acadêmica e produtos comerciais, com mais de 22 milhões de downloads. Também é bem reconhecido pela comunidade de aprendizado de máquina com vários posts/tutoriais dedicados, incluindo Analytics Vidhya, KDnuggets e Towards Data Science.
PyOD é apresentado para :
- Interface unificada e fácil de usar em vários algoritmos.
- Ampla variedade de modelos , desde técnicas clássicas até os mais recentes métodos de aprendizado profundo em PyTorch .
- Alto desempenho e eficiência , aproveitando numba e joblib para compilação JIT e processamento paralelo.
- Treinamento e previsão rápidos , alcançados por meio da estrutura SUOD [50].
Detecção de outlier com 5 linhas de código :
# Example: Training an ECOD detector
from pyod . models . ecod import ECOD
clf = ECOD ()
clf . fit ( X_train )
y_train_scores = clf . decision_scores_ # Outlier scores for training data
y_test_scores = clf . decision_function ( X_test ) # Outlier scores for test data
Selecionando o algoritmo certo: não sabe por onde começar? Considere estas opções robustas e interpretáveis:
- ECOD: Exemplo de uso de ECOD para detecção de valores discrepantes
- Floresta de isolamento: exemplo de uso da floresta de isolamento para detecção de valores discrepantes
Alternativamente, explore o MetaOD para uma abordagem baseada em dados.
Citando PyOD :
O artigo PyOD é publicado no Journal of Machine Learning Research (JMLR) (faixa MLOSS). Se você usar PyOD em uma publicação científica, agradeceríamos citações do seguinte artigo:
@artigo{zhao2019pyod,
autor = {Zhao, Yue e Nasrullah, Zain e Li, Zheng},
title = {PyOD: uma caixa de ferramentas Python para detecção escalável de outliers},
diário = {Journal of Machine Learning Research},
ano = {2019},
volume = {20},
número = {96},
páginas = {1-7},
url={http://jmlr.org/papers/v20/19-011.html}
}
ou:
Zhao, Y., Nasrullah, Z. e Li, Z., 2019. PyOD: uma caixa de ferramentas Python para detecção escalável de outliers. Jornal de pesquisa de aprendizado de máquina (JMLR), 20(96), pp.1-7.
Para uma perspectiva mais ampla sobre detecção de anomalias, consulte nossos artigos NeurIPS ADBench: Anomaly Detection Benchmark Paper e ADGym: Design Choices for Deep Anomaly Detection:
@artigo{han2022adbench,
title={Adbench: benchmark de detecção de anomalias},
autor = {Han, Songqiao e Hu, Xiyang e Huang, Hailiang e Jiang, Minqi e Zhao, Yue},
journal={Avanços em sistemas de processamento de informações neurais},
volume={35},
páginas={32142--32159},
ano={2022}
}
@artigo{jiang2023adgym,
title={ADGym: opções de design para detecção de anomalias profundas},
autor = {Jiang, Minqi e Hou, Chaochuan e Zheng, Ao e Han, Songqiao e Huang, Hailiang e Wen, Qingsong e Hu, Xiyang e Zhao, Yue},
journal={Avanços em Sistemas de Processamento de Informações Neurais},
volume={36},
ano={2023}
}
Índice :
- Instalação
- Folha de dicas e referência da API
- Benchmark e conjuntos de dados do ADBench
- Salvar e carregar modelo
- Trem rápido com SUOD
- Limiar de pontuações atípicas
- Algoritmos Implementados
- Início rápido para detecção de valores discrepantes
- Como contribuir
- Critérios de inclusão
Instalação
PyOD foi projetado para fácil instalação usando pip ou conda . Recomendamos usar a versão mais recente do PyOD devido às atualizações e melhorias frequentes:
pip install pyod # normal install
pip install --upgrade pyod # or update if needed
conda install -c conda-forge pyod
Alternativamente, você pode clonar e executar o arquivo setup.py:
git clone https://github.com/yzhao062/pyod.git
cd pyod
pip install .
Dependências necessárias :
- Python 3.8 ou superior
- joblib
- matplotlib
- entorpecido>=1,19
- número>=0,51
- scipy>=1.5.1
- scikit_learn>=0.22.0
Dependências opcionais (veja detalhes abaixo) :
- combo (opcional, necessário para models/combination.py e FeatureBagging)
- pytorch (opcional, necessário para AutoEncoder e outros modelos de aprendizado profundo)
- suod (opcional, necessário para executar o modelo SUOD)
- xgboost (opcional, necessário para XGBOD)
- pythresh (opcional, necessário para limite)
Folha de dicas e referência da API
A referência completa da API está disponível na documentação do PyOD. Abaixo está uma folha de dicas rápida para todos os detectores:
- fit(X) : Ajusta o detector. O parâmetro y é ignorado em métodos não supervisionados.
- Decision_function(X) : Preveja pontuações brutas de anomalia para X usando o detector ajustado.
- prever (X) : determine se uma amostra é atípica ou não como rótulos binários usando o detector ajustado.
- predizer_proba(X) : Estime a probabilidade de uma amostra ser atípica usando o detector ajustado.
- predizer_confidence(X) : Avalie a confiança do modelo por amostra (aplicável em predizer e prever_proba) [35].
Principais atributos de um modelo ajustado :
- Decision_scores_ : pontuações atípicas dos dados de treinamento. Pontuações mais altas normalmente indicam comportamento mais anormal. Outliers geralmente têm pontuações mais altas.
- rótulos_ : rótulos binários dos dados de treinamento, onde 0 indica valores discrepantes e 1 indica valores discrepantes/anomalias.
Benchmark e conjuntos de dados do ADBench
Acabamos de lançar um ADBench mais abrangente de 45 páginas: Benchmark de detecção de anomalias [15]. O ADBench de código aberto compara 30 algoritmos de detecção de anomalias em 57 conjuntos de dados de benchmark.
A organização do ADBench é fornecida abaixo:

Para uma visualização mais simples, fazemos a comparação dos modelos selecionados via compare_all_models.py.
Salvar e carregar modelo
PyOD adota uma abordagem semelhante ao sklearn em relação à persistência do modelo. Consulte persistência do modelo para esclarecimentos.
Resumindo, recomendamos usar joblib ou pickle para salvar e carregar modelos PyOD. Consulte "examples/save_load_model_example.py" para obter um exemplo. Resumindo, é simples como abaixo:
from joblib import dump , load
# save the model
dump ( clf , 'clf.joblib' )
# load the model
clf = load ( 'clf.joblib' )
Sabe-se que existem desafios em salvar modelos de redes neurais. Verifique #328 e #88 para soluções temporárias.
Trem rápido com SUOD
Treinamento e previsão rápidos : é possível treinar e prever com um grande número de modelos de detecção em PyOD aproveitando a estrutura SUOD [50]. Veja o artigo SUOD e o exemplo SUOD.
from pyod . models . suod import SUOD
# initialized a group of outlier detectors for acceleration
detector_list = [ LOF ( n_neighbors = 15 ), LOF ( n_neighbors = 20 ),
LOF ( n_neighbors = 25 ), LOF ( n_neighbors = 35 ),
COPOD (), IForest ( n_estimators = 100 ),
IForest ( n_estimators = 200 )]
# decide the number of parallel process, and the combination method
# then clf can be used as any outlier detection model
clf = SUOD ( base_estimators = detector_list , n_jobs = 2 , combination = 'average' ,
verbose = False )
Limiar de pontuações atípicas
Uma abordagem mais baseada em dados pode ser adotada ao definir o nível de contaminação. Ao usar um método de limiar, adivinhar um valor arbitrário pode ser substituído por técnicas testadas para separar valores discrepantes e discrepantes. Consulte PyThresh para uma visão mais aprofundada do limite.
from pyod . models . knn import KNN
from pyod . models . thresholds import FILTER
# Set the outlier detection and thresholding methods
clf = KNN ( contamination = FILTER ())
Consulte os métodos de limite suportados em limite.
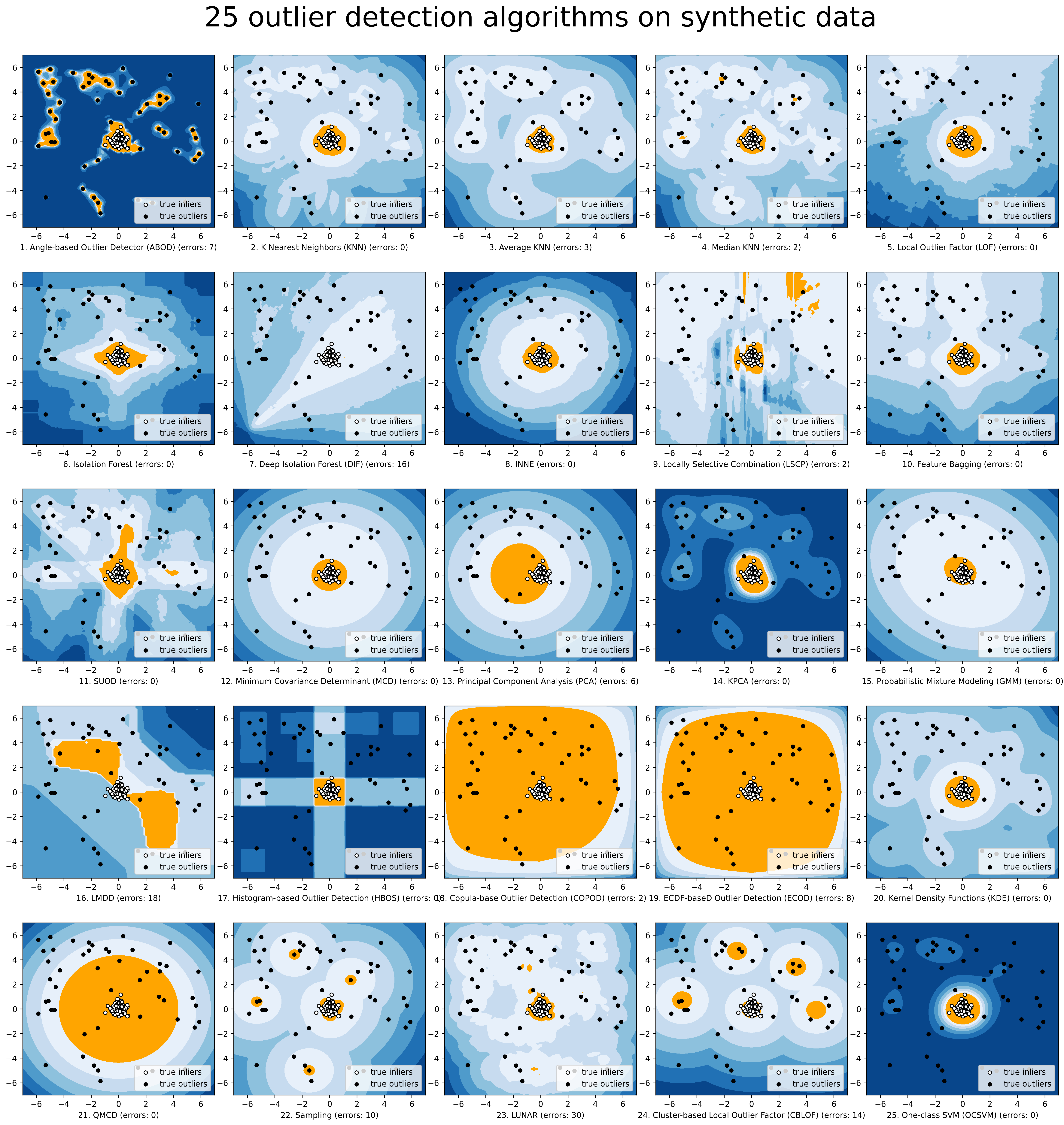
Algoritmos Implementados
O kit de ferramentas PyOD consiste em quatro grupos funcionais principais:
(i) Algoritmos de Detecção Individual :
| Tipo | Abre | Algoritmo | Ano | Referência |
|---|
| Probabilístico | ECOD | Detecção de valores discrepantes não supervisionados usando funções de distribuição cumulativa empírica | 2022 | [28] |
| Probabilístico | ABOD | Detecção de valores discrepantes baseada em ângulo | 2008 | [22] |
| Probabilístico | Rápido ABOD | Detecção rápida de outliers baseada em ângulo usando aproximação | 2008 | [22] |
| Probabilístico | COPOD | COPOD: detecção de outliers baseada em cópula | 2020 | [27] |
| Probabilístico | LOUCO | Desvio Absoluto Mediano (MAD) | 1993 | [19] |
| Probabilístico | SOS | Seleção Estocástica de Outliers | 2012 | [20] |
| Probabilístico | QMCD | Detecção de discrepância de quase Monte Carlo | 2001 | [11] |
| Probabilístico | KDE | Detecção de valores discrepantes com funções de densidade do kernel | 2007 | [24] |
| Probabilístico | Amostragem | Detecção rápida de valores discrepantes com base em distância por meio de amostragem | 2013 | [42] |
| Probabilístico | GMM | Modelagem Probabilística de Mistura para Análise Outlier | | [1] [Cap.2] |
| Modelo Linear | PCA | Análise de componentes principais (a soma das distâncias projetadas ponderadas para os hiperplanos de vetores próprios) | 2003 | [41] |
| Modelo Linear | KPCA | Análise de componentes principais do kernel | 2007 | [18] |
| Modelo Linear | DCM | Determinante de covariância mínima (use as distâncias de mahalanobis como pontuações discrepantes) | 1999 | [16] [37] |
| Modelo Linear | CD | Use a distância de Cook para detecção de valores discrepantes | 1977 | [10] |
| Modelo Linear | OCSVM | Máquinas de vetores de suporte de classe única | 2001 | [40] |
| Modelo Linear | LMDD | Detecção de valores discrepantes baseada em desvio (LMDD) | 1996 | [6] |
| Baseado em proximidade | LOF | Fator atípico local | 2000 | [8] |
| Baseado em proximidade | COF | Fator atípico baseado em conectividade | 2002 | [43] |
| Baseado em proximidade | (Incremental) COF | Fator atípico baseado em conectividade com eficiência de memória (mais lento, mas reduz a complexidade do armazenamento) | 2002 | [43] |
| Baseado em proximidade | CBLOF | Fator atípico local baseado em cluster | 2003 | [17] |
| Baseado em proximidade | LOCI | LOCI: Detecção rápida de valores discrepantes usando a integral de correlação local | 2003 | [33] |
| Baseado em proximidade | HBOS | Pontuação Outlier baseada em histograma | 2012 | [12] |
| Baseado em proximidade | kNN | k Vizinhos mais próximos (use a distância até o k-ésimo vizinho mais próximo como pontuação atípica) | 2000 | [36] |
| Baseado em proximidade | Média KNN | KNN médio (use a distância média até k vizinhos mais próximos como pontuação atípica) | 2002 | [5] |
| Baseado em proximidade | MedKNN | Mediana kNN (use a distância mediana até k vizinhos mais próximos como pontuação atípica) | 2002 | [5] |
| Baseado em proximidade | SOD | Detecção de outliers subespaciais | 2009 | [23] |
| Baseado em proximidade | HASTE | Detecção de valores discrepantes baseada em rotação | 2020 | [4] |
| Conjuntos atípicos | IForest | Floresta de Isolamento | 2008 | [29] |
| Conjuntos atípicos | INNE | Detecção de anomalias baseada em isolamento usando conjuntos de vizinhos mais próximos | 2018 | [7] |
| Conjuntos atípicos | DIF | Floresta de isolamento profundo para detecção de anomalias | 2023 | [45] |
| Conjuntos atípicos | Facebook | Ensacamento de recursos | 2005 | [25] |
| Conjuntos atípicos | LSCP | LSCP: Combinação Localmente Seletiva de Conjuntos Outliers Paralelos | 2019 | [49] |
| Conjuntos atípicos | XGBOD | Detecção de valores discrepantes com base em reforço extremo (supervisionado) | 2018 | [48] |
| Conjuntos atípicos | LODA | Detector on-line leve de anomalias | 2016 | [34] |
| Conjuntos atípicos | SUOD | SUOD: Acelerando a detecção de valores discrepantes heterogêneos não supervisionados em grande escala (aceleração) | 2021 | [50] |
| Redes Neurais | AutoEncoder | AutoEncoder totalmente conectado (use erro de reconstrução como pontuação atípica) | | [1] [Cap.3] |
| Redes Neurais | VAE | AutoEncoder Variacional (use erro de reconstrução como pontuação atípica) | 2013 | [21] |
| Redes Neurais | Beta-VAE | AutoEncoder Variacional (todos os termos de perda personalizados variando gama e capacidade) | 2018 | [9] |
| Redes Neurais | SO_GAAL | Aprendizagem Ativa Adversarial Gerativa de Objetivo Único | 2019 | [30] |
| Redes Neurais | MO_GAAL | Aprendizagem Ativa Adversarial Gerativa de Múltiplos Objetivos | 2019 | [30] |
| Redes Neurais | DeepSVDD | Classificação profunda de uma classe | 2018 | [38] |
| Redes Neurais | AnoGAN | Detecção de anomalias com redes adversárias generativas | 2017 | [39] |
| Redes Neurais | ALAD | Detecção de anomalia aprendida adversamente | 2018 | [47] |
| Redes Neurais | AE1SVM | Máquina de vetores de suporte de classe única baseada em autoencoder | 2019 | [31] |
| Redes Neurais | DevNet | Detecção profunda de anomalias com redes de desvio | 2019 | [32] |
| Baseado em gráfico | Gráfico R | Detecção de outlier por gráfico R | 2017 | [46] |
| Baseado em gráfico | LUNAR | LUNAR: Unificando métodos locais de detecção de outliers por meio de redes neurais gráficas | 2022 | [13] |
(ii) Estruturas de combinação de conjuntos de outliers e detectores de outliers :
| Tipo | Abre | Algoritmo | Ano | Referência |
|---|
| Conjuntos atípicos | Facebook | Ensacamento de recursos | 2005 | [25] |
| Conjuntos atípicos | LSCP | LSCP: Combinação Localmente Seletiva de Conjuntos Outliers Paralelos | 2019 | [49] |
| Conjuntos atípicos | XGBOD | Detecção de valores discrepantes com base em reforço extremo (supervisionado) | 2018 | [48] |
| Conjuntos atípicos | LODA | Detector on-line leve de anomalias | 2016 | [34] |
| Conjuntos atípicos | SUOD | SUOD: Acelerando a detecção de valores discrepantes heterogêneos não supervisionados em grande escala (aceleração) | 2021 | [50] |
| Conjuntos atípicos | INNE | Detecção de anomalias baseada em isolamento usando conjuntos de vizinhos mais próximos | 2018 | [7] |
| Combinação | Média | Combinação simples calculando a média das pontuações | 2015 | [2] |
| Combinação | Média Ponderada | Combinação simples calculando a média das pontuações com pesos de detector | 2015 | [2] |
| Combinação | Maximização | Combinação simples obtendo as pontuações máximas | 2015 | [2] |
| Combinação | AOM | Média do Máximo | 2015 | [2] |
| Combinação | MOA | Maximização da Média | 2015 | [2] |
| Combinação | Mediana | Combinação simples tomando a mediana das pontuações | 2015 | [2] |
| Combinação | Votação majoritária | Combinação simples obtendo a maioria dos votos dos rótulos (podem ser usados pesos) | 2015 | [2] |
(iii) Funções Utilitárias :
| Tipo | Nome | Função | Documentação |
|---|
| Dados | gerar_dados | Geração de dados sintetizados; os dados normais são gerados por uma Gaussiana multivariada e os valores discrepantes são gerados por uma distribuição uniforme | gerar_dados |
| Dados | gerar_data_clusters | Geração de dados sintetizados em clusters; padrões de dados mais complexos podem ser criados com vários clusters | gerar_data_clusters |
| Estatística | wpearsonr | Calcule a correlação ponderada de Pearson de duas amostras | wpearsonr |
| Utilitário | get_label_n | Transforme pontuações atípicas brutas em rótulos binários, atribuindo 1 às n pontuações atípicas | get_label_n |
| Utilitário | precisão_n_pontuações | calcular precisão @ classificação n | precisão_n_pontuações |
Início rápido para detecção de valores discrepantes
PyOD foi bem reconhecido pela comunidade de aprendizado de máquina com algumas postagens e tutoriais em destaque.
Analytics Vidhya : um tutorial incrível para aprender a detecção de outliers em Python usando a biblioteca PyOD
KDnuggets : visualização intuitiva de métodos de detecção de valores discrepantes, uma visão geral dos métodos de detecção de valores discrepantes do PyOD
Rumo à ciência de dados : detecção de anomalias para leigos
"examples/knn_example.py" demonstra a API básica do uso do detector kNN. Observa-se que a API em todos os outros algoritmos é consistente/semelhante .
Instruções mais detalhadas para a execução de exemplos podem ser encontradas no diretório de exemplos.
Inicialize um detector kNN, ajuste o modelo e faça a previsão.
from pyod . models . knn import KNN # kNN detector
# train kNN detector
clf_name = 'KNN'
clf = KNN ()
clf . fit ( X_train )
# get the prediction label and outlier scores of the training data
y_train_pred = clf . labels_ # binary labels (0: inliers, 1: outliers)
y_train_scores = clf . decision_scores_ # raw outlier scores
# get the prediction on the test data
y_test_pred = clf . predict ( X_test ) # outlier labels (0 or 1)
y_test_scores = clf . decision_function ( X_test ) # outlier scores
# it is possible to get the prediction confidence as well
y_test_pred , y_test_pred_confidence = clf . predict ( X_test , return_confidence = True ) # outlier labels (0 or 1) and confidence in the range of [0,1]
Avalie a previsão por ROC e Precision @ Rank n (p@n).
from pyod . utils . data import evaluate_print
# evaluate and print the results
print ( " n On Training Data:" )
evaluate_print ( clf_name , y_train , y_train_scores )
print ( " n On Test Data:" )
evaluate_print ( clf_name , y_test , y_test_scores )
Veja um exemplo de saída e visualização.
On Training Data :
KNN ROC : 1.0 , precision @ rank n : 1.0
On Test Data :
KNN ROC : 0.9989 , precision @ rank n : 0.9
visualize ( clf_name , X_train , y_train , X_test , y_test , y_train_pred ,
y_test_pred , show_figure = True , save_figure = False )
Visualização (knn_figure):
Referência
| [1] | (1, 2) Aggarwal, CC, 2015. Análise de outliers. Em Mineração de dados (pp. 237-263). Springer, Cham. |
| [2] | (1, 2, 3, 4, 5, 6, 7) Aggarwal, CC e Sathe, S., 2015. Fundamentos teóricos e algoritmos para conjuntos discrepantes. Boletim Informativo de Explorações ACM SIGKDD , 17(1), pp.24-47. |
| [3] | Aggarwal, CC e Sathe, S., 2017. Conjuntos discrepantes: uma introdução. Springer. |
| [4] | Almardeny, Y., Boujnah, N. e Cleary, F., 2020. Um novo método de detecção de outliers para dados multivariados. Transações IEEE sobre Engenharia de Conhecimento e Dados . |
| [5] | (1, 2) Angiulli, F. e Pizzuti, C., 2002, agosto. Detecção rápida de valores discrepantes em espaços de alta dimensão. Na Conferência Europeia sobre Princípios de Mineração de Dados e Descoberta de Conhecimento, pp. |
| [6] | Arning, A., Agrawal, R. e Raghavan, P., 1996, agosto. Um método linear para detecção de desvios em grandes bancos de dados. Em KDD (Vol. 1141, No. 50, pp. 972-981). |
| [7] | (1, 2) Bandaragoda, TR, Ting, KM, Albrecht, D., Liu, FT, Zhu, Y., e Wells, JR, 2018, Detecção de anomalias baseada em isolamento usando conjuntos de vizinhos mais próximos. Inteligência Computacional , 34(4), pp. |
| [8] | Breunig, MM, Kriegel, HP, Ng, RT e Sander, J., 2000, maio. LOF: identificação de valores discrepantes locais com base na densidade. Registro ACM Sigmod , 29(2), pp. |
| [9] | Burgess, Christopher P., et al. "Compreendendo o desembaraço em beta-VAE." pré-impressão arXiv arXiv:1804.03599 (2018). |
| [10] | Cook, RD, 1977. Detecção de observação influente na regressão linear. Tecnometria, 19(1), pp.15-18. |
| [11] | Fang, KT e Ma, CX, 2001. Discrepância L2 envolvente de amostragem aleatória, hipercubo latino e designs uniformes. Revista de complexidade, 17(4), pp.608-624. |
| [12] | Goldstein, M. e Dengel, A., 2012. Pontuação discrepante baseada em histograma (hbos): Um algoritmo rápido de detecção de anomalias não supervisionadas. Em KI-2012: Pôster e faixa de demonstração , pp.59-63. |
| [13] | Goodge, A., Hooi, B., Ng, SK e Ng, WS, 2022, junho. Lunar: Unificando métodos locais de detecção de valores discrepantes por meio de redes neurais gráficas. Nos Anais da Conferência AAAI sobre Inteligência Artificial. |
| [14] | Gopalan, P., Sharan, V. e Wieder, U., 2019. PIDForest: detecção de anomalias por meio de identificação parcial. Em Avanços em Sistemas de Processamento de Informação Neural, pp. |
| [15] | Han, S., Hu, X., Huang, H., Jiang, M. e Zhao, Y., 2022. ADBench: Benchmark de detecção de anomalias. Pré-impressão do arXiv arXiv:2206.09426. |
| [16] | Hardin, J. e Rocke, DM, 2004. Detecção de outliers no cenário de múltiplos clusters usando o estimador do determinante de covariância mínima. Estatística Computacional e Análise de Dados , 44(4), pp.625-638. |
| [17] | He, Z., Xu, X. e Deng, S., 2003. Descobrindo valores discrepantes locais baseados em cluster. Cartas de reconhecimento de padrões , 24(9-10), pp.1641-1650. |
| [18] | Hoffmann, H., 2007. Kernel PCA para detecção de novidades. Reconhecimento de padrões, 40(3), pp.863-874. |
| [19] | Iglewicz, B. e Hoaglin, DC, 1993. Como detectar e lidar com outliers (Vol. 16). Asq Press. |
| [20] | Janssens, JHM, Huszár, F., Postma, EO e van den Herik, HJ, 2012. Seleção estocástica de valores discrepantes. Relatório técnico TiCC TR 2012-001, Universidade de Tilburg, Centro de Cognição e Comunicação de Tilburg, Tilburg, Holanda. |
| [21] | Kingma, DP e Welling, M., 2013. Bayes variacionais de autocodificação. Pré-impressão do arXiv arXiv:1312.6114. |
| [22] | (1, 2) Kriegel, HP e Zimek, A., 2008, agosto. Detecção de valores discrepantes baseada em ângulo em dados de alta dimensão. Em KDD '08 , pp. ACM. |
| [23] | Kriegel, HP, Kröger, P., Schubert, E. e Zimek, A., 2009, abril. Detecção de outliers em subespaços paralelos ao eixo de dados de alta dimensão. Na Conferência Pacífico-Ásia sobre Descoberta de Conhecimento e Mineração de Dados , pp. Springer, Berlim, Heidelberg. |
| [24] | Latecki, LJ, Lazarevic, A. e Pokrajac, D., 2007, julho. Detecção de outliers com funções de densidade de kernel. No Workshop Internacional sobre Aprendizado de Máquina e Mineração de Dados em Reconhecimento de Padrões (pp. 61-75). Springer, Berlim, Heidelberg. |
| [25] | (1, 2) Lazarevic, A. e Kumar, V., 2005, agosto. Ensacamento de recursos para detecção de valores discrepantes. Em KDD '05 . 2005. |
| [26] | Li, D., Chen, D., Jin, B., Shi, L., Goh, J. e Ng, SK, 2019, setembro. MAD-GAN: Detecção multivariada de anomalias para dados de séries temporais com redes adversárias generativas. Na Conferência Internacional sobre Redes Neurais Artificiais (pp. 703-716). Springer, Cham. |
| [27] | Li, Z., Zhao, Y., Botta, N., Ionescu, C. e Hu, X. COPOD: Detecção de outlier baseada em cópula. Conferência Internacional IEEE sobre Mineração de Dados (ICDM) , 2020. |
| [28] | Li, Z., Zhao, Y., Hu, X., Botta, N., Ionescu, C. e Chen, HG ECOD: Detecção de outlier não supervisionada usando funções de distribuição cumulativa empírica. Transações IEEE sobre Engenharia de Conhecimento e Dados (TKDE) , 2022. |
| [29] | Liu, FT, Ting, KM e Zhou, ZH, 2008, dezembro. Floresta de isolamento. Na Conferência Internacional sobre Mineração de Dados , pp. IEEE. |
| [30] | (1, 2) Liu, Y., Li, Z., Zhou, C., Jiang, Y., Sun, J., Wang, M. e He, X., 2019. Aprendizagem ativa adversária generativa para detecção de valores discrepantes não supervisionados . Transações IEEE sobre Engenharia de Conhecimento e Dados . |
| [31] | Nguyen, MN e Vien, NA, 2019. SVMS de uma classe escaláveis e interpretáveis com aprendizado profundo e recursos aleatórios de Fourier. Em Aprendizado de Máquina e Descoberta de Conhecimento em Bancos de Dados: Conferência Europeia , ECML PKDD, 2018. |
| [32] | Pang, Guansong, Chunhua Shen e Anton Van Den Hengel. "Detecção profunda de anomalias com redes de desvio." Em KDD , pp. 2019. |
| [33] | Papadimitriou, S., Kitagawa, H., Gibbons, PB e Faloutsos, C., 2003, março. LOCI: Detecção rápida de outliers usando a integral de correlação local. Em ICDE '03 , pp. IEEE. |
| [34] | (1, 2) Pevný, T., 2016. Loda: Detector on-line leve de anomalias. Aprendizado de Máquina , 102(2), pp.275-304. |
| [35] | Perini, L., Vercruyssen, V., Davis, J. Quantificando a confiança dos detectores de anomalias em suas previsões baseadas em exemplos. Na Conferência Europeia Conjunta sobre Aprendizado de Máquina e Descoberta de Conhecimento em Bancos de Dados (ECML-PKDD) , 2020. |
| [36] | Ramaswamy, S., Rastogi, R. e Shim, K., 2000, maio. Algoritmos eficientes para extrair valores discrepantes de grandes conjuntos de dados. Registro ACM Sigmod , 29(2), pp. |
| [37] | Rousseeuw, PJ e Driessen, KV, 1999. Um algoritmo rápido para o estimador do determinante de covariância mínima. Tecnometria , 41(3), pp.212-223. |
| [38] | Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Siddiqui, SA, Binder, A., Müller, E. e Kloft, M., 2018, julho. Classificação profunda de uma classe. Na conferência internacional sobre aprendizado de máquina (pp. 4393-4402). PMLR. |
| [39] | Schlegl, T., Seeböck, P., Waldstein, SM, Schmidt-Erfurth, U. e Langs, G., 2017, junho. Detecção de anomalias não supervisionada com redes adversárias generativas para orientar a descoberta de marcadores. Na conferência internacional sobre processamento de informações em imagens médicas (pp. 146-157). Springer, Cham. |
| [40] | Scholkopf, B., Platt, JC, Shawe-Taylor, J., Smola, AJ e Williamson, RC, 2001. Estimando o suporte de uma distribuição de alta dimensão. Computação Neural , 13(7), pp.1443-1471. |
| [41] | Shyu, ML, Chen, SC, Sarinnapakorn, K. e Chang, L., 2003. Um novo esquema de detecção de anomalias baseado no classificador de componentes principais. MIAMI UNIV CORAL GABLES FL DEPARTAMENTO DE ENGENHARIA ELÉTRICA E DE COMPUTAÇÃO . |
| [42] | Sugiyama, M. e Borgwardt, K., 2013. Detecção rápida de valores discrepantes baseada em distância por meio de amostragem. Avanços em sistemas de processamento de informação neural, 26. |
| [43] | (1, 2) Tang, J., Chen, Z., Fu, AWC e Cheung, DW, 2002, maio. Melhorando a eficácia das detecções de valores discrepantes para padrões de baixa densidade. Na Conferência Pacífico-Ásia sobre Descoberta de Conhecimento e Mineração de Dados , pp. Springer, Berlim, Heidelberg. |
| [44] | Wang, X., Du, Y., Lin, S., Cui, P., Shen, Y. e Yang, Y., 2019. adVAE: Um autoencoder variacional autoadversarial com conhecimento prévio de anomalia gaussiana para detecção de anomalias. Sistemas Baseados em Conhecimento . |
| [45] | Xu, H., Pang, G., Wang, Y., Wang, Y., 2023. Floresta de isolamento profundo para detecção de anomalias. Transações IEEE sobre Engenharia de Conhecimento e Dados . |
| [46] | You, C., Robinson, DP e Vidal, R., 2017. Auto-representação provável com base na detecção de valores discrepantes em uma união de subespaços. Em Anais da conferência IEEE sobre visão computacional e reconhecimento de padrões. |
| [47] | Zenati, H., Romain, M., Foo, CS, Lecouat, B. e Chandrasekhar, V., 2018, novembro. Detecção de anomalias aprendidas adversamente. Em 2018, conferência internacional IEEE sobre mineração de dados (ICDM) (pp. 727-736). IEEE. |
| [48] | (1, 2) Zhao, Y. e Hryniewicki, MK XGBOD: Melhorando a detecção supervisionada de outliers com aprendizagem de representação não supervisionada. Conferência Conjunta Internacional IEEE sobre Redes Neurais , 2018. |
| [49] | (1, 2) Zhao, Y., Nasrullah, Z., Hryniewicki, MK e Li, Z., 2019, maio. LSCP: Combinação localmente seletiva em conjuntos paralelos de outliers. Em Anais da Conferência Internacional SIAM sobre Mineração de Dados (SDM) 2019 , pp. Sociedade de Matemática Industrial e Aplicada. |
| [50] | (1, 2, 3, 4) Zhao, Y., Hu, X., Cheng, C., Wang, C., Wan, C., Wang, W., Yang, J., Bai, H., Li , Z., Xiao, C., Wang, Y., Qiao, Z., Sun, J. e Akoglu, L. (2021). SUOD: Acelerando a detecção de valores discrepantes heterogêneos não supervisionados em grande escala. Conferência sobre Aprendizado de Máquina e Sistemas (MLSys) . |


