Download stumpy - download do código fonte stumpy

Status do teste

atarracado

STUMPY é uma biblioteca Python poderosa e escalonável que calcula com eficiência algo chamado perfil de matriz, que é apenas uma forma acadêmica de dizer "para cada subsequência (verde) em sua série temporal, identifique automaticamente seu vizinho mais próximo correspondente (cinza)":

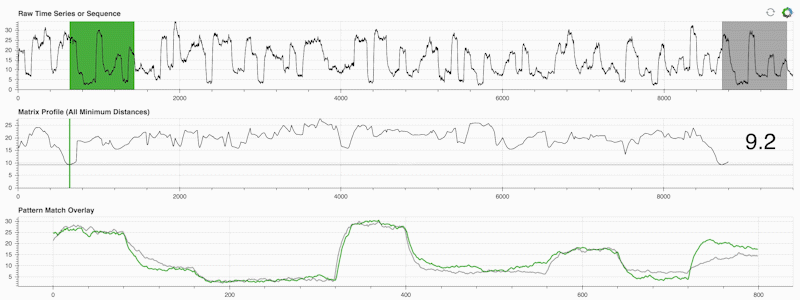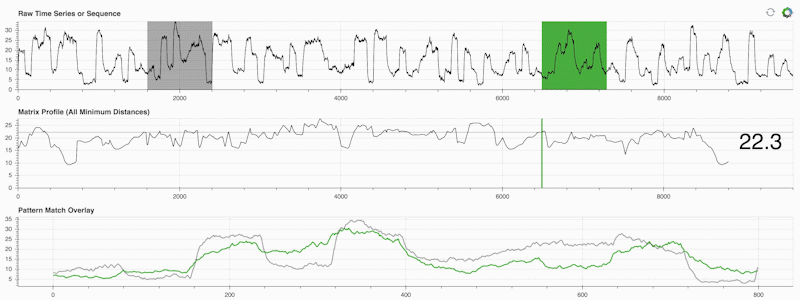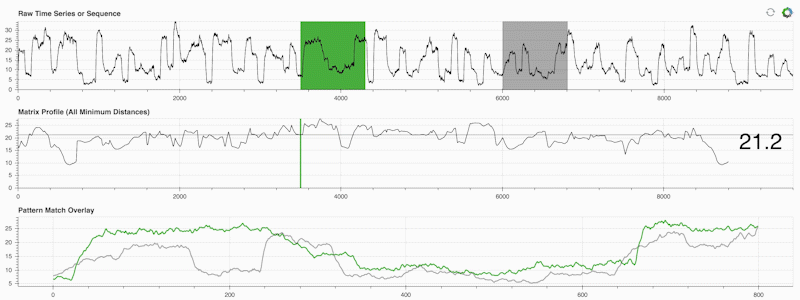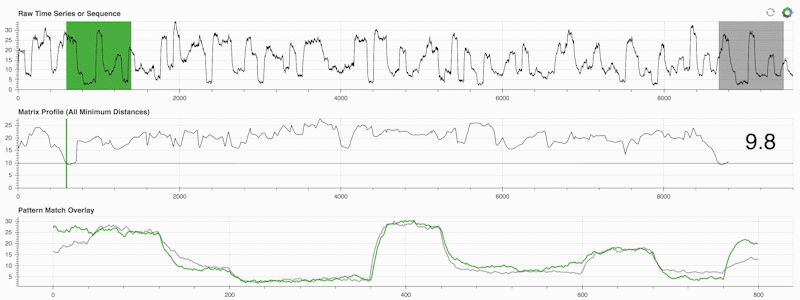
GIF animado

O importante é que, depois de calcular seu perfil de matriz (painel central acima), ele poderá ser usado para uma variedade de tarefas de mineração de dados de séries temporais, como:

descoberta de padrão/motivo (subsequências aproximadamente repetidas dentro de uma série temporal mais longa)
descoberta de anomalia/novidade (discórdia)
descoberta de shapelet
segmentação semântica
streaming de dados (on-line)
perfis de matriz aproximados rápidos
cadeias de séries temporais (conjunto ordenado temporalmente de padrões de subsequência)
trechos para resumir séries temporais longas
perfis pan-matrix para selecionar o(s) melhor(es) tamanho(s) de janela de subsequência
e mais ...

Quer você seja um acadêmico, cientista de dados, desenvolvedor de software ou entusiasta de séries temporais, o STUMPY é simples de instalar e nosso objetivo é permitir que você obtenha insights de séries temporais com mais rapidez. Consulte a documentação para obter mais informações.

Como usar o STUMPY

Consulte nossa documentação da API para obter uma lista completa de funções disponíveis e nossos tutoriais informativos para exemplos de casos de uso mais abrangentes. Abaixo, você encontrará trechos de código que demonstram rapidamente como usar o STUMPY.

Uso típico (dados de série temporal unidimensionais) com STUMP:

 import stumpy
import numpy as np

if __name__ == "__main__" :
    your_time_series = np . random . rand ( 10000 )
    window_size = 50  # Approximately, how many data points might be found in a pattern

    matrix_profile = stumpy . stump ( your_time_series , m = window_size )

Uso distribuído para dados de série temporal unidimensionais com Dask Distribuído via STUMPED:

 import stumpy
import numpy as np
from dask . distributed import Client

if __name__ == "__main__" :
    with Client () as dask_client :
        your_time_series = np . random . rand ( 10000 )
        window_size = 50  # Approximately, how many data points might be found in a pattern

        matrix_profile = stumpy . stumped ( dask_client , your_time_series , m = window_size )

Uso de GPU para dados de série temporal unidimensionais com GPU-STUMP:

 import stumpy
import numpy as np
from numba import cuda

if __name__ == "__main__" :
    your_time_series = np . random . rand ( 10000 )
    window_size = 50  # Approximately, how many data points might be found in a pattern
    all_gpu_devices = [ device . id for device in cuda . list_devices ()]  # Get a list of all available GPU devices

    matrix_profile = stumpy . gpu_stump ( your_time_series , m = window_size , device_id = all_gpu_devices )

Dados de série temporal multidimensionais com MSTUMP:

 import stumpy
import numpy as np

if __name__ == "__main__" :
    your_time_series = np . random . rand ( 3 , 1000 )  # Each row represents data from a different dimension while each column represents data from the same dimension
    window_size = 50  # Approximately, how many data points might be found in a pattern

    matrix_profile , matrix_profile_indices = stumpy . mstump ( your_time_series , m = window_size )

Análise distribuída de dados de séries temporais multidimensionais com Dask Distributed MSTUMPED:

 import stumpy
import numpy as np
from dask . distributed import Client

if __name__ == "__main__" :
    with Client () as dask_client :
        your_time_series = np . random . rand ( 3 , 1000 )   # Each row represents data from a different dimension while each column represents data from the same dimension
        window_size = 50  # Approximately, how many data points might be found in a pattern

        matrix_profile , matrix_profile_indices = stumpy . mstumped ( dask_client , your_time_series , m = window_size )

Cadeias de série temporal com cadeias de série temporal ancoradas (ATSC):

 import stumpy
import numpy as np

if __name__ == "__main__" :
    your_time_series = np . random . rand ( 10000 )
    window_size = 50  # Approximately, how many data points might be found in a pattern

    matrix_profile = stumpy . stump ( your_time_series , m = window_size )

    left_matrix_profile_index = matrix_profile [:, 2 ]
    right_matrix_profile_index = matrix_profile [:, 3 ]
    idx = 10  # Subsequence index for which to retrieve the anchored time series chain for

    anchored_chain = stumpy . atsc ( left_matrix_profile_index , right_matrix_profile_index , idx )

    all_chain_set , longest_unanchored_chain = stumpy . allc ( left_matrix_profile_index , right_matrix_profile_index )

Segmentação Semântica com Segmentação Semântica Unipotente Rápida e de Baixo Custo (FLUSS):

 import stumpy
import numpy as np

if __name__ == "__main__" :
    your_time_series = np . random . rand ( 10000 )
    window_size = 50  # Approximately, how many data points might be found in a pattern

    matrix_profile = stumpy . stump ( your_time_series , m = window_size )

    subseq_len = 50
    correct_arc_curve , regime_locations = stumpy . fluss ( matrix_profile [:, 1 ],
                                                    L = subseq_len ,
                                                    n_regimes = 2 ,
                                                    excl_factor = 1
                                                    )

Dependências

As versões suportadas de Python e NumPy são determinadas de acordo com a política de descontinuação NEP 29.

NumPy
Numba
SciPy

Onde conseguir

Instalação Conda (preferencial):

conda install -c conda-forge stumpy

Instalação do PyPI, presumindo que você tenha numpy, scipy e numba instalados:

python -m pip install stumpy

Para instalar o stumpy a partir do código-fonte, consulte as instruções na documentação.

Documentação

Para compreender e apreciar totalmente os algoritmos e aplicações subjacentes, é fundamental que você leia as publicações originais. Para um exemplo mais detalhado de como usar o STUMPY, consulte a documentação mais recente ou explore nossos tutoriais práticos.

Desempenho

Testamos o desempenho do cálculo do perfil de matriz exato usando a versão compilada Numba JIT do código em dados de série temporal gerados aleatoriamente com vários comprimentos (ou seja, np.random.rand(n) ) junto com diferentes recursos de hardware de CPU e GPU.

Os resultados brutos são exibidos na tabela abaixo como Horas:Minutos:Segundos.Milisegundos e com um tamanho de janela constante de m = 50. Observe que esses tempos de execução relatados incluem o tempo que leva para mover os dados do host para todos os Dispositivo(s) GPU. Talvez seja necessário rolar para o lado direito da tabela para ver todos os tempos de execução.

eu	n = 2 ^eu	GPU-STOMP	TOCO.2	TOCO.16	PERSOCADO.128	PERSOCADO.256	GPU-STUMP.1	GPU-STUMP.2	GPU-STUMP.DGX1	GPU-STUMP.DGX2
6	64	00:00:10,00	00:00:00,00	00:00:00,00	00:00:05,77	00:00:06,08	00:00:00,03	00:00:01,63	NaN	NaN
7	128	00:00:10,00	00:00:00,00	00:00:00,00	00:00:05,93	00:00:07,29	00:00:00,04	00:00:01,66	NaN	NaN
8	256	00:00:10,00	00:00:00,00	00:00:00,01	00:00:05,95	00:00:07,59	00:00:00,08	00:00:01,69	00:00:06,68	00:00:25,68
9	512	00:00:10,00	00:00:00,00	00:00:00,02	00:00:05,97	00:00:07,47	00:00:00,13	00:00:01,66	00:00:06,59	00:00:27,66
10	1024	00:00:10,00	00:00:00,02	00:00:00,04	00:00:05,69	00:00:07,64	00:00:00,24	00:00:01,72	00:00:06,70	00:00:30,49
11	2048	NaN	00:00:00,05	00:00:00,09	00:00:05,60	00:00:07,83	00:00:00,53	00:00:01,88	00:00:06,87	00:00:31,09
12	4096	NaN	00:00:00,22	00:00:00,19	00:00:06,26	00:00:07,90	00:00:01.04	00:00:02,19	00:00:06,91	00:00:33,93
13	8192	NaN	00:00:00,50	00:00:00,41	00:00:06,29	00:00:07,73	00:00:01,97	00:00:02,49	00:00:06,61	00:00:33,81
14	16384	NaN	00:00:01,79	00:00:00,99	00:00:06,24	00:00:08,18	00:00:03,69	00:00:03,29	00:00:07,36	00:00:35,23
15	32768	NaN	00:00:06,17	00:00:02,39	00:00:06,48	00:00:08,29	00:00:07,45	00:00:04,93	00:00:07,02	00:00:36,09
16	65536	NaN	00:00:22,94	00:00:06,42	00:00:07,33	00:00:09,01	00:00:14,89	00:00:08,12	00:00:08,10	00:00:36,54
17	131072	00:00:10,00	00:01:29,27	00:00:19,52	00:00:09,75	00:00:10,53	00:00:29,97	00:00:15,42	00:00:09,45	00:00:37,33
18	262144	00:00:18,00	00:05:56,50	00:01:08,44	00:00:33,38	00:00:24,07	00:00:59,62	00:00:27,41	00:00:13,18	00:00:39,30
19	524288	00:00:46,00	00:25:34,58	00:03:56,82	00:01:35,27	00:03:43,66	00:01:56,67	00:00:54,05	00:00:19,65	00:00:41,45
20	1048576	00:02:30,00	01:51:13,43	00:19:54,75	00:04:37,15	00:03:01,16	00:05:06,48	00:02:24,73	00:00:32,95	00:00:46,14
21	2097152	00:09:15,00	09:25:47,64	03:05:07,64	00:13:36,51	00:08:47,47	00:20:27,94	00:09:41,43	00:01:06,51	00:01:02,67
22	4194304	NaN	36:12:23,74	10:37:51,21	00:55:44,43	00:32:06,70	01:21:12,33	00:38:30,86	00:04:03,26	00:02:23,47
23	8388608	NaN	143:16:09,94	38:42:51,42	03:33:30,53	02:00:49,37	05:11:44,45	02:33:14,60	00:15:46,26	00:08:03,76
24	16777216	NaN	NaN	NaN	14:39:11,99	07:13:47,12	20:43:03,80	09:48:43,42	01:00:24,06	00:29:07,84
NaN	17729800	09:16:12,00	NaN	NaN	15:31:31,75	07:18:42,54	23:09:22,43	10:54:08,64	01:07:35,39	00:32:51,55
25	33554432	NaN	NaN	NaN	56:03:46,81	26:27:41,29	83:29:21,06	39:17:43,82	03:59:32,79	01:54:56,52
26	67108864	NaN	NaN	NaN	211:17:37,60	106:40:17,17	328:58:04,68	157:18:30,50	15:42:15,94	07:18:52,91
NaN	100000000	291:07:12,00	NaN	NaN	NaN	234:51:35,39	NaN	NaN	35:03:44,61	16:22:40,81
27	134217728	NaN	NaN	NaN	NaN	NaN	NaN	NaN	64:41:55,09	29:13:48,12

Recursos de hardware

GPU-STOMP: Esses resultados são reproduzidos do artigo Matrix Profile II original - NVIDIA Tesla K80 (contém 2 GPUs) e servem como referência de desempenho para comparação.

STUMP.2: stumpy.stump executado com 2 CPUs no total - 2x processadores Intel(R) Xeon(R) CPU E5-2650 v4 @ 2,20GHz paralelizados com Numba em um único servidor sem Dask.

STUMP.16: stumpy.stump executado com 16 CPUs no total - 16x processadores Intel(R) Xeon(R) CPU E5-2650 v4 @ 2,20GHz paralelizados com Numba em um único servidor sem Dask.

STUMPED.128: stumpy.stumped executado com 128 CPUs no total - 8x processadores Intel(R) Xeon(R) CPU E5-2650 v4 @ 2,20GHz x 16 servidores, paralelizados com Numba e distribuídos com Dask Distributed.

STUMPED.256: stumpy.stumped executado com 256 CPUs no total - 8x processadores Intel(R) Xeon(R) CPU E5-2650 v4 @ 2,20GHz x 32 servidores, paralelizados com Numba e distribuídos com Dask Distributed.

GPU-STUMP.1: stumpy.gpu_stump executado com 1 GPU NVIDIA GeForce GTX 1080 Ti, 512 threads por bloco, limite de potência de 200 W, compilado para CUDA com Numba e paralelizado com multiprocessamento Python

GPU-STUMP.2: stumpy.gpu_stump executado com 2x GPU NVIDIA GeForce GTX 1080 Ti, 512 threads por bloco, limite de potência de 200 W, compilado para CUDA com Numba e paralelizado com multiprocessamento Python

GPU-STUMP.DGX1: stumpy.gpu_stump executado com 8x NVIDIA Tesla V100, 512 threads por bloco, compilado para CUDA com Numba e paralelizado com multiprocessamento Python

GPU-STUMP.DGX2: stumpy.gpu_stump executado com 16x NVIDIA Tesla V100, 512 threads por bloco, compilado para CUDA com Numba e paralelizado com multiprocessamento Python

Executando testes

Os testes são escritos no diretório tests e processados usando PyTest e requerem coverage.py para análise de cobertura de código. Os testes podem ser executados com:

./test.sh

Versão Python

STUMPY suporta Python 3.9+ e, devido ao uso de nomes/identificadores de variáveis unicode, não é compatível com Python 2.x. Dadas as pequenas dependências, o STUMPY pode funcionar em versões mais antigas do Python, mas isso está além do escopo do nosso suporte e recomendamos fortemente que você atualize para a versão mais recente do Python.

Obtendo ajuda

Primeiro, verifique as discussões e questões no Github para ver se sua pergunta já foi respondida lá. Se nenhuma solução estiver disponível, sinta-se à vontade para abrir uma nova discussão ou questão e os autores tentarão responder em tempo razoável.

Contribuindo

Aceitamos contribuições de qualquer forma! Assistência com documentação, especialmente tutoriais em expansão, é sempre bem-vinda. Para contribuir, faça um fork do projeto, faça suas alterações e envie uma solicitação pull. Faremos o nosso melhor para resolver quaisquer problemas com você e mesclar seu código no branch principal.

Citando

Se você usou esta base de código em uma publicação científica e deseja citá-la, use o artigo do Journal of Open Source Software.

Lei SM, (2019). STUMPY: uma biblioteca Python poderosa e escalável para mineração de dados de séries temporais . Jornal de Software de Código Aberto, 4(39), 1504.

 @article { law2019stumpy ,
  author  = { Law, Sean M. } ,
  title   = { {STUMPY: A Powerful and Scalable Python Library for Time Series Data Mining} } ,
  journal = { {The Journal of Open Source Software} } ,
  volume  = { 4 } ,
  number  = { 39 } ,
  pages   = { 1504 } ,
  year    = { 2019 }
}

Referências

Sim, Chin-Chia Michael, et al. (2016) Perfil de matriz I: junções de similaridade de todos os pares para séries temporais: uma visão unificadora que inclui motivos, discordâncias e shapelets. ICDM:1317-1322. Link

Zhu, Yan, et al. (2016) Matrix Profile II: Explorando um novo algoritmo e GPUs para quebrar a barreira dos cem milhões para motivos e junções de séries temporais. ICDM:739-748. Link

Sim, Chin-Chia Michael, et al. (2017) Matrix Profile VI: descoberta significativa de motivos multidimensionais. ICDM:565-574. Link

Zhu, Yan, et al. (2017) Matrix Profile VII: Cadeias de séries temporais: um novo primitivo para mineração de dados de séries temporais. ICDM:695-704. Link

Gharghabi, Shaghayegh, et al. (2017) Matrix Profile VIII: Segmentação Semântica Online Agnóstica de Domínio em Níveis de Desempenho Sobre-humanos. ICDM:117-126. Link

Zhu, Yan, et al. (2017) Explorando um novo algoritmo e GPUs para quebrar a barreira de dez quatrilhões de comparações entre pares para motivos e junções de séries temporais. KAIS:203-236. Link

Zhu, Yan, et al. (2018) Matrix Profile XI: SCRIMP++: Descoberta de motivos de séries temporais em velocidades interativas. ICDM:837-846. Link

Sim, Chin-Chia Michael, et al. (2018) Junções de séries temporais, motivos, discórdias e shapelets: uma visão unificadora que explora o perfil da matriz. Disco de conhecimento mínimo de dados: 83-123. Link

Gharghabi, Shaghayegh, et al. (2018) "Matrix Profile XII: MPdist: Uma nova medida de distância de série temporal para permitir a mineração de dados em cenários mais desafiadores." ICDM:965-970. Link

Zimmerman, Zachary, et al. (2019) Matrix Profile XIV: Dimensionando a descoberta de motivos de séries temporais com GPUs para quebrar um quintilhão de comparações de pares por dia e além. SoCC '19:74-86. Link

Akbarinia, Reza e Betrand Cloez. (2019) Computação eficiente de perfis matriciais usando diferentes funções de distância. arXiv:1901.05708. Link

Kamgar, Kaveh, et al. (2019) Matrix Profile XV: Explorando motivos de consenso de séries temporais para encontrar estrutura em conjuntos de séries temporais. ICDM:1156-1161. Link