Início | Instalação | Documentação | Tutorial | Desenvolvedores
rodeo é uma biblioteca Python rápida que usa números probabilísticos para resolver equações diferenciais ordinárias (EDOs). Ou seja, a maioria dos solucionadores de EDO (como o método de Euler) produzem uma aproximação determinística para a EDO em uma grade de tamanho de passo
rodeo fornece uma família leve e extensível de aproximações para um paradigma de filtragem bayesiana não linear comum a muitos solucionadores probabilísticos (Tronarp et al (2018)). Isso começa colocando um processo gaussiano antes da solução ODE e atualizando-o sequencialmente à medida que o solucionador percorre a grade. rodeo é construído em jax , o que permite compilação just-in-time e diferenciação automática. A API do jax é quase equivalente à do numpy .
rodeo fornece duas ferramentas principais: uma para aproximar a solução EDO e outra para inferência de parâmetros. Para o primeiro, fornecemos:
solve : Implementação de um solucionador ODE probabilístico que usa um paradigma de filtragem bayesiana não linear.Para este último, fornecemos os métodos de aproximação de verossimilhança:
basic : Implementação de um método básico de aproximação de verossimilhança (detalhes podem ser encontrados em Wu e Lysy (2023)).fenrir : Implementação do Fenrir (Tronarp et al (2022)).marginal_mcmc : implementação MCMC do método Chkrebtii (Chkrebtii et al (2016)).dalton : Implementação de nossa aproximação de probabilidade EDO adaptativa a dados (Wu e Lysy (2023)).Exemplos detalhados de seu uso podem ser encontrados na seção Documentação. Observe que esta é a versão do rodeo somente para jax . Para as versões legadas usando vários outros back-ends, veja aqui.
Baixe o repositório do GitHub e instale com o script setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . Primeiro vá para readthedocs para ver a documentação renderizada para os exemplos a seguir.
Um tutorial de início rápido sobre como resolver um problema simples de EDO.
Um exemplo para resolver uma EDO de ordem superior.
Um exemplo para resolver uma EDO caótica difícil.
Um exemplo de problema de inferência de parâmetros onde usamos a aproximação de Laplace.
Neste passo a passo, mostramos como resolver uma EDO com nosso solucionador probabilístico e como conduzir inferência de parâmetros. Iremos primeiro ilustrar a configuração para resolver a EDO. Para tanto, vamos considerar o seguinte exemplo de EDO de primeira ordem (modelo FitzHugh-Nagumo ),
onde a solução
Seguindo a notação de (Wu e Lysy (2023)), temos
para
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) Comparamos a solução do solucionador com a solução determinística fornecida pelo odeint na biblioteca scipy .
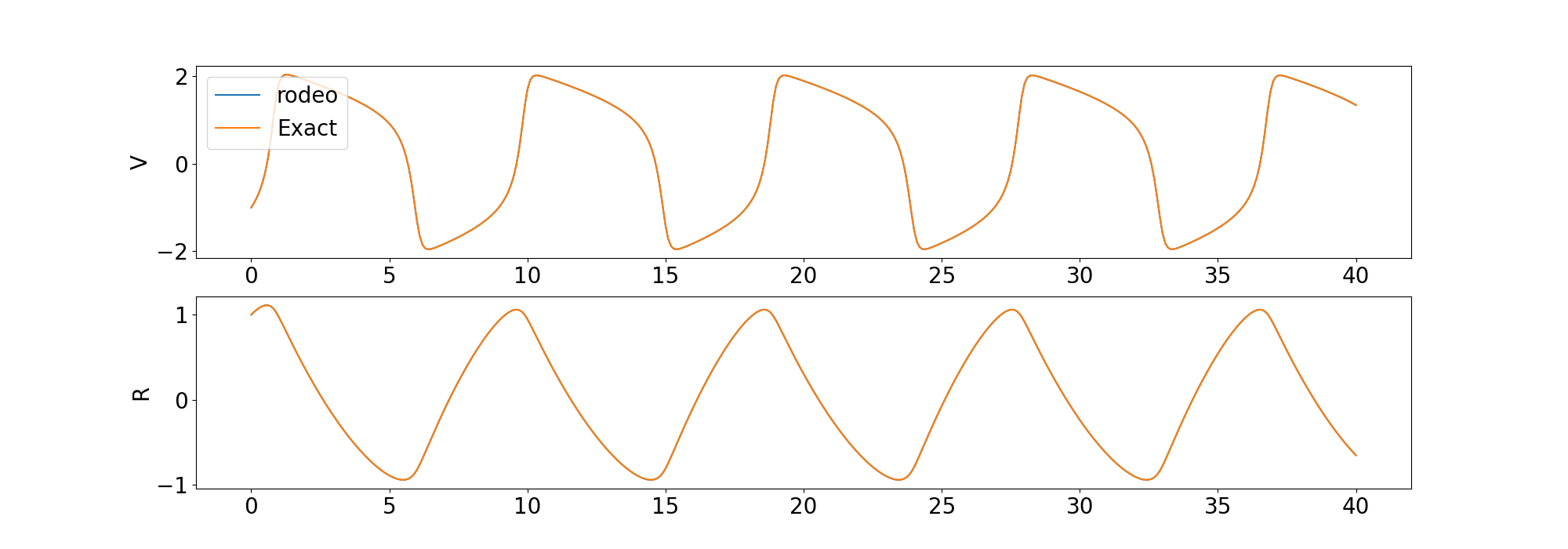
Também incluímos exemplos para resolver uma EDO de ordem superior e uma EDO caótica.
Passamos agora para o problema de inferência de parâmetros. rodeo contém vários métodos de aproximação de verossimilhança resumidos na seção Descrição. Aqui, usaremos o método basic de aproximação de verossimilhança. Suponha que as observações sejam simuladas por meio do modelo
onde basic para
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) Este é um exemplo básico para demonstrar o uso. Sugerimos aproximações de verossimilhança mais sofisticadas que propagam a incerteza da solução para a aproximação de verossimilhança, como fenrir , marginal_mcmc e dalton . Consulte o tutorial de inferência de parâmetros para obter mais detalhes.
Aqui estão alguns resultados produzidos por várias aproximações de probabilidade encontradas no rodeio de /examples/ :
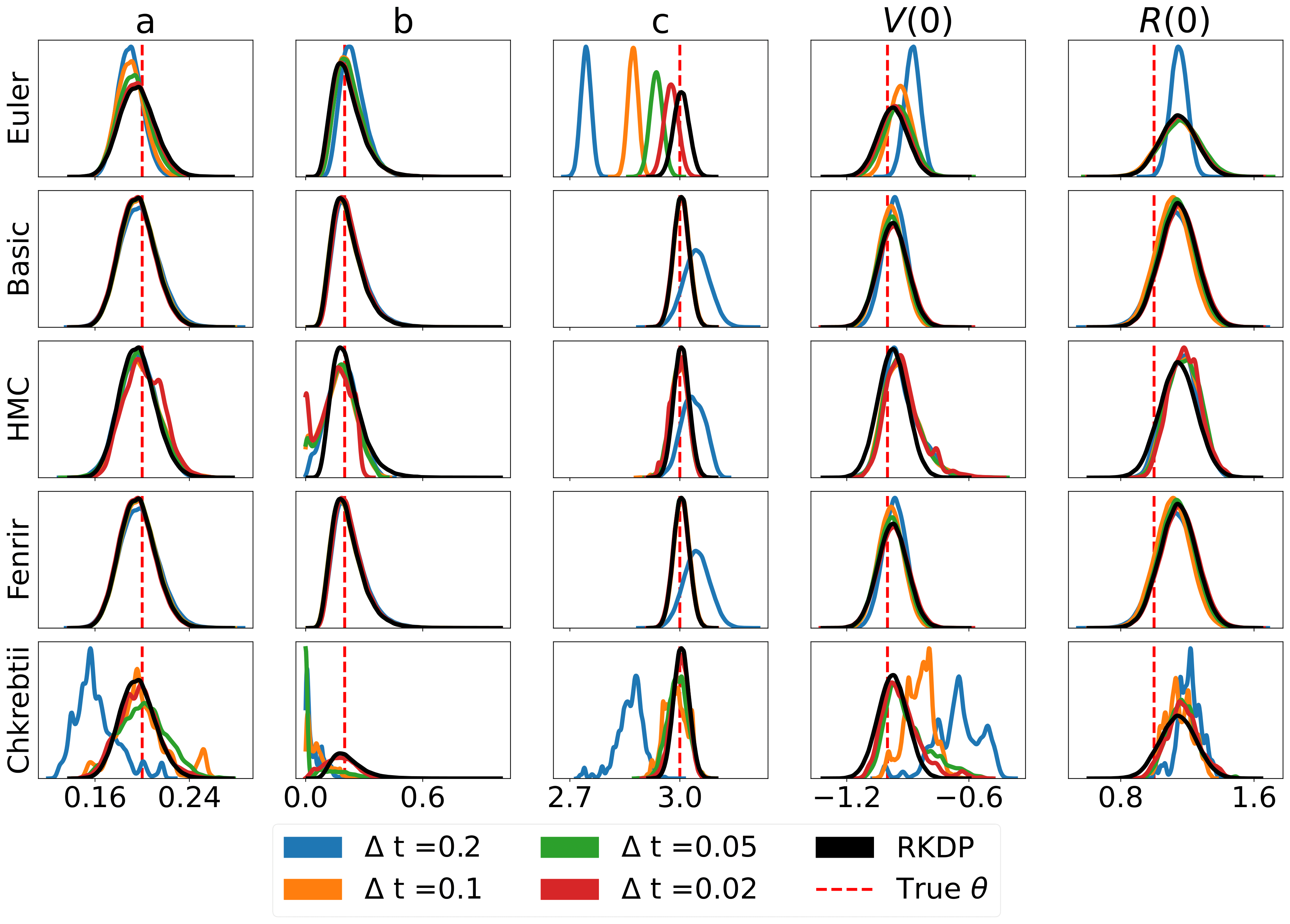
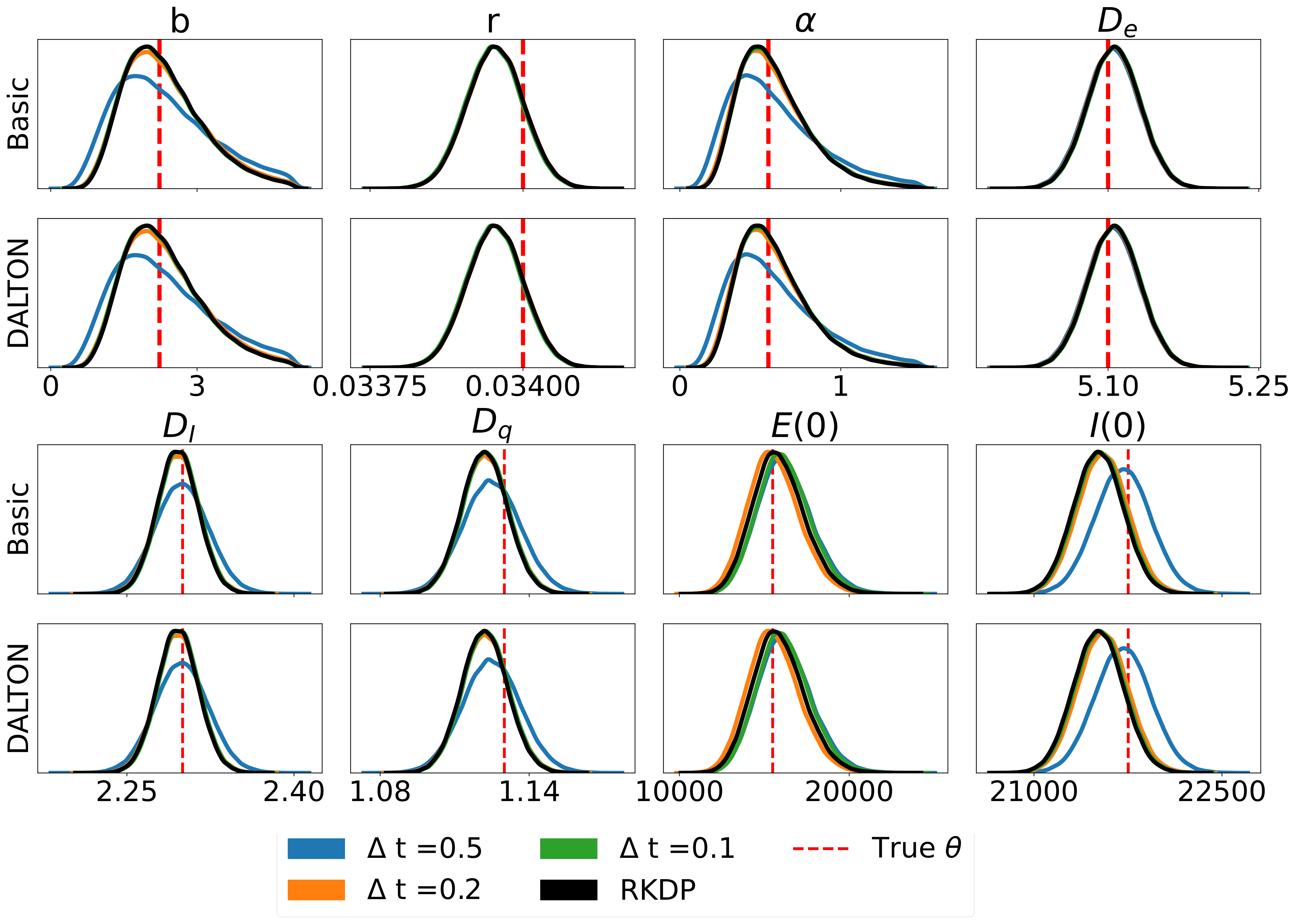
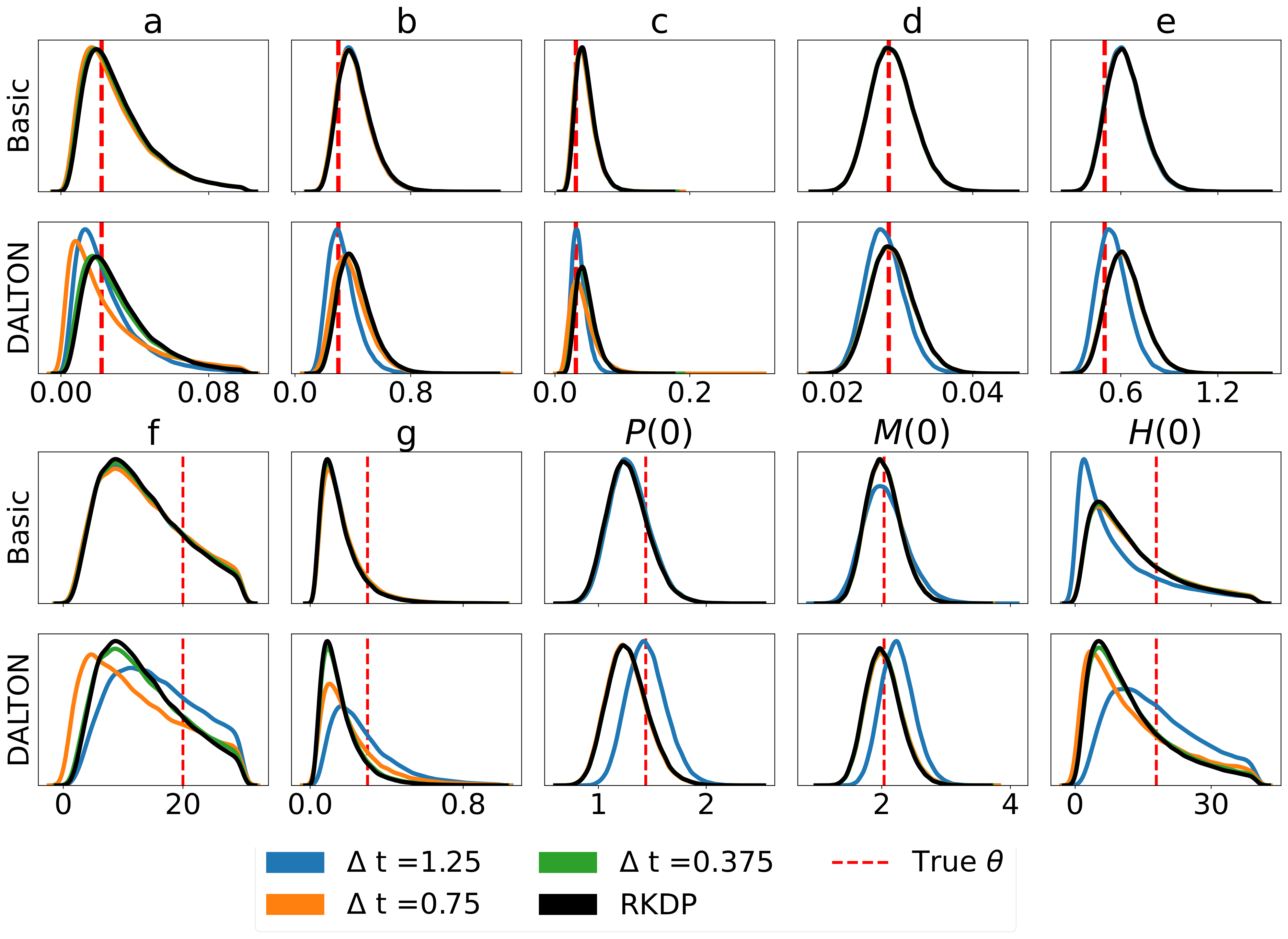
Os testes unitários podem ser executados através dos seguintes comandos:
cd tests
python -m unittest discover -v Ou instale tox e, em rodeo digite a linha de comando: tox .
A documentação HTML pode ser compilada a partir da pasta raiz:
pip install .[docs]
cd docs
make html Isso criará a documentação em docs/build .