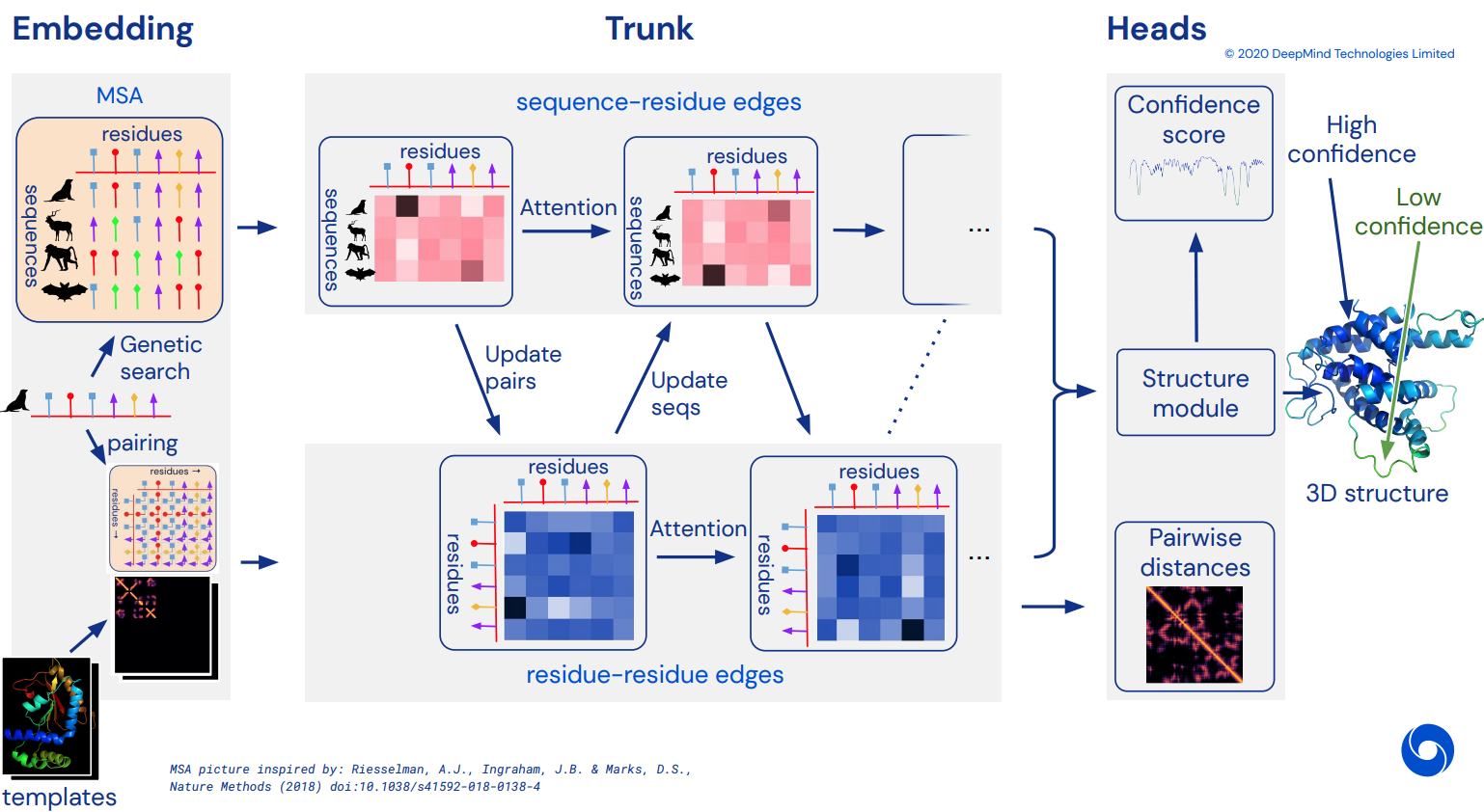
Para eventualmente se tornar uma implementação Pytorch não oficial do Alphafold2, a rede de atenção de tirar o fôlego que resolveu o CASP14. Será implementado gradualmente à medida que mais detalhes da arquitetura forem divulgados.
Assim que isso for replicado, pretendo dobrar todas as sequências de aminoácidos disponíveis in-silico e liberá-las como uma torrente acadêmica, para promover a ciência. Se você estiver interessado em esforços de replicação, visite #alphafold neste canal do Discord
Atualização: Deepmind abriu o código oficial em Jax, junto com os pesos! Este repositório agora será voltado para uma tradução direta de pytorch com algumas melhorias na codificação posicional
Vídeo ArxivInsights
$ pip install alphafold2-pytorchlhatsk relatou treinar um tronco modificado deste repositório, usando a mesma configuração do trRosetta, com resultados competitivos
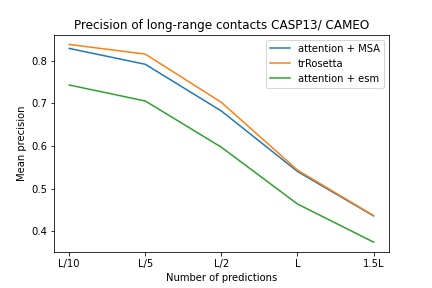
blue used the the trRosetta input (MSA -> potts -> axial attention), green used the ESM embedding (only sequence) -> tiling -> axial attention - lhatsk
Prever distograma, como Alphafold-1, mas com atenção
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
reversible = False # set this to True for fully reversible self / cross attention for the trunk
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda () # AA length of 128
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda () # MSA doesn't have to be the same length as primary sequence
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Você também pode ativar a previsão para os ângulos, passando um predict_angles = True no init. O exemplo abaixo seria equivalente a trRosetta, mas com atenção própria/cruzada.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_angles = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram , theta , phi , omega = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
)
# distogram - (1, 128, 128, 37),
# theta - (1, 128, 128, 25),
# phi - (1, 128, 128, 13),
# omega - (1, 128, 128, 25) O artigo recente de Fabian sugere que alimentar iterativamente as coordenadas de volta ao SE3 Transformer, com peso compartilhado, pode funcionar. Decidi executar com base nessa ideia, embora ainda não se saiba como realmente funciona.
Você também pode usar E(n)-Transformer ou EGNN para refinamento estrutural.
Atualização: O laboratório de Baker mostrou que uma arquitetura ponta a ponta de sequência e embeddings MSA para transformadores SE3 pode ser melhor trRosetta e fechar a lacuna para Alphafold2. Estaremos utilizando o Graph Transformer, que atua nos embeddings do tronco, para gerar o conjunto inicial de coordenadas a ser enviado à rede equivariante. (Isso é ainda corroborado por Costa et al em seu trabalho revelando coordenadas 3D de embeddings do MSA Transformer em um artigo anterior ao laboratório Baker)
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
structure_module_type = 'se3' , # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
structure_module_dim = 4 , # se3 transformer dimension
structure_module_depth = 1 , # depth
structure_module_heads = 1 , # heads
structure_module_dim_head = 16 , # dimension of heads
structure_module_refinement_iters = 2 , # number of equivariant coordinate refinement iterations
structure_num_global_nodes = 1 # number of global nodes for the structure module, only works with SE3 transformer
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue A suposição subjacente é que o tronco funciona no nível do resíduo e, em seguida, constitui o nível atômico para o módulo de estrutura, seja ele Transformadores SE3, Transformador E (n) ou EGNN fazendo o refinamento. O padrão desta biblioteca são os 3 átomos de backbone (C, Ca, N), mas você pode configurá-la para incluir qualquer outro átomo que desejar, incluindo Cb e as cadeias laterais.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
atoms = 'backbone-with-cbeta'
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 4, 3) <-- 4 atoms per residue (C, Ca, N, Cb) As escolhas válidas para atoms incluem:
backbone - 3 átomos de backbone (C, Ca, N) [padrão]backbone-with-cbeta - 3 átomos de backbone e C betabackbone-with-oxygen - 3 átomos de espinha dorsal e oxigênio da carboxilabackbone-with-cbeta-and-oxygen - 3 átomos de espinha dorsal com C beta e oxigênioall - backbone e todos os outros átomos da cadeia lateralVocê também pode passar um tensor de forma (14), definindo quais átomos você gostaria de incluir
ex.
atoms = torch . tensor ([ 1 , 1 , 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 ])Este repositório oferece um complemento fácil à rede com embeddings pré-treinados do Facebook AI. Ele contém wrappers para ESM, MSA Transformers ou Protein Transformer pré-treinados.
Existem alguns pré-requisitos. Você precisará certificar-se de ter a biblioteca apex da Nvidia instalada, pois os transformadores pré-treinados fazem uso de algumas operações fundidas.
Ou você pode tentar executar o script abaixo
git clone https://github.com/NVIDIA/apex
cd apex
pip install -v --disable-pip-version-check --no-cache-dir --global-option= " --cpp_ext " --global-option= " --cuda_ext " ./ Em seguida, você simplesmente terá que importar e agrupar sua instância Alphafold2 com um ESMEmbedWrapper , MSAEmbedWrapper ou ProtTranEmbedWrapper e ele se encarregará de incorporar a sequência e os alinhamentos de múltiplas sequências para você (e projetá-los nas dimensões especificadas em seu modelo). Nada precisa ser alterado, exceto a adição do wrapper.
import torch
from alphafold2_pytorch import Alphafold2
from alphafold2_pytorch . embeds import MSAEmbedWrapper
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64
)
model = MSAEmbedWrapper (
alphafold2 = alphafold2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) Por padrão, mesmo que o wrapper forneça ao tronco a sequência e os embeddings MSA, eles serão somados com os embeddings de token usuais. Se você deseja treinar Alphafold2 sem embeddings de token (confiar apenas em embeddings pré-treinados), você precisará definir disable_token_embed como True na inicialização Alphafold2 .
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
disable_token_embed = True
) Um artigo de Jinbo Xu sugere que não é necessário descartar as distâncias e, em vez disso, é possível prever a média e o desvio padrão diretamente. Você pode usar isso ativando um sinalizador predict_real_value_distances ; nesse caso, a previsão de distância retornada terá uma dimensão de 2 para a média e o desvio padrão, respectivamente.
Se predict_coords também estiver ativado, o MDS aceitará as previsões de média e desvio padrão diretamente, sem precisar calculá-las a partir dos compartimentos do distograma.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
predict_real_value_distances = True , # set this to True
structure_module_type = 'se3' ,
structure_module_dim = 4 ,
structure_module_depth = 1 ,
structure_module_heads = 1 ,
structure_module_dim_head = 16 ,
structure_module_refinement_iters = 2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Você pode adicionar blocos convolucionais, tanto para a sequência primária quanto para o MSA, simplesmente definindo um argumento de palavra-chave extra use_conv = True
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37)Os kernels convolucionais seguem o exemplo deste artigo, combinando kernels 1d e 2d em um bloco semelhante a resnet. Você pode personalizar totalmente os kernels como tal.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
conv_seq_kernels = (( 9 , 1 ), ( 1 , 9 ), ( 3 , 3 )), # kernels for N x N primary sequence
conv_msa_kernels = (( 1 , 9 ), ( 3 , 3 )), # kernels for {num MSAs} x N MSAs
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Você também pode fazer a dilatação do ciclo com um argumento de palavra-chave extra. A dilatação padrão é 1 para todas as camadas.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
dilations = ( 1 , 3 , 5 ) # cycle between dilations of 1, 3, 5
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Finalmente, em vez de seguir o padrão de convoluções, autoatenção, atenção cruzada por repetição de profundidade, você pode personalizar qualquer ordem que desejar com a palavra-chave custom_block_types
ex. Uma rede onde você faz predominantemente convoluções primeiro, seguidas por blocos de autoatenção + atenção cruzada
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
heads = 8 ,
dim_head = 64 ,
custom_block_types = (
* (( 'conv' ,) * 6 ),
* (( 'self' , 'cross' ) * 6 )
)
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Você pode treinar com Sparse Attention do Microsoft Deepspeed, mas terá que suportar o processo de instalação. São duas etapas.
Primeiro, você precisa instalar o Deepspeed com Sparse Attention
$ sh install_deepspeed.sh Em seguida, você precisa instalar o pacote pip triton
$ pip install tritonSe ambas as opções acima deram certo, agora você pode treinar com Sparse Attention!
Infelizmente, a atenção escassa só é apoiada pela atenção própria, e não pela atenção cruzada. Trarei uma solução diferente para melhorar o desempenho da atenção cruzada.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
max_seq_len = 2048 , # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
sparse_self_attn = ( True , False ) * 6 # interleave sparse and full attention for all 12 layers
). cuda ()Também adicionei uma das melhores variantes de atenção linear, na esperança de diminuir o fardo do atendimento cruzado. Pessoalmente, não achei que o Performer funcionasse tão bem, mas como no artigo eles relataram alguns números bons para benchmarks de proteínas, pensei em incluí-lo e permitir que outros experimentassem.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = True # simply set this to True to use Performer for all cross attention
). cuda ()Você também pode especificar as camadas exatas que deseja usar a atenção linear, passando uma tupla do mesmo comprimento que a profundidade
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = ( True , False ) * 3 # interleave linear and full attention
). cuda ()Este artigo sugere que, se você tiver consultas ou contextos que definiram axiais (digamos, uma imagem), poderá reduzir a quantidade de atenção necessária calculando a média desses axiais (altura e largura) e concatenando os axiais médios em uma sequência. Você pode ativar isso como uma técnica de economia de memória para a atenção cruzada, especificamente para a sequência primária.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_kron_primary = True # make sure primary sequence undergoes the kronecker operator during cross attention
). cuda () Você também pode aplicar o mesmo operador aos MSAs durante a atenção cruzada com o sinalizador cross_attn_kron_msa , se seus MSAs estiverem alinhados e tiverem a mesma largura.
Pendência
Para economizar memória para atenção cruzada, você pode definir uma taxa de compactação para chaves/valores, seguindo o esquema apresentado neste artigo. Uma taxa de compressão de 2-4 é geralmente aceitável.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_compress_ratio = 3
). cuda ()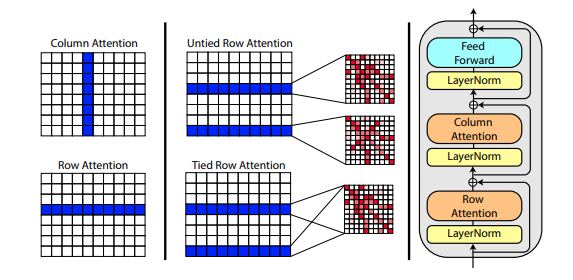
Um novo artigo de Roshan Rao propõe o uso de atenção axial para pré-treinamento em MSA. Dados os bons resultados, este repositório utilizará o mesmo esquema no tronco, especificamente para o autoatendimento do MSA.
Você também pode vincular as atenções de linha do MSA com a configuração msa_tie_row_attn = True na inicialização de Alphafold2 . No entanto, para usar isso, você deve certificar-se de que, se tiver um número ímpar de MSAs por sequência primária, a máscara MSA esteja definida corretamente como False para as linhas que não estão em uso.
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
msa_tie_row_attn = True # just set this to true
)O processamento do modelo também é feito em grande parte com atenção axial, com atenção cruzada feita ao longo da dimensão do número de modelos. Isso segue em grande parte o mesmo esquema da recente abordagem de toda a atenção para classificação de vídeo, mostrada aqui.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randint ( 0 , 37 , ( 1 , 2 , 16 , 3 )). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_coors = templates_coors ,
templates_mask = templates_mask
)Se as informações da cadeia lateral também estiverem presentes, na forma do vetor unitário entre as coordenadas C e C-alfa de cada resíduo, você também pode passá-las da seguinte maneira.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randn ( 1 , 2 , 16 , 3 ). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
templates_sidechains = torch . randn ( 1 , 2 , 16 , 3 ). cuda () # unit vectors of difference of C and C-alpha coordinates
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_mask = templates_mask ,
templates_coors = templates_coors ,
templates_sidechains = templates_sidechains
)Preparei uma reimplementação do SE3 Transformer, conforme explicado por Fabian Fuchs em uma postagem especulativa no blog.
Além disso, um novo artigo de Victor e Welling usa recursos invariantes para equivariância E(n), alcançando SOTA e superando o SE3 Transformer em vários benchmarks, sendo ao mesmo tempo muito mais rápido. Peguei as ideias principais deste artigo e modifiquei-o para se tornar um transformador (acrescentei atenção aos recursos e às atualizações de coordenadas).
Todas as três redes equivariantes acima foram integradas e estão disponíveis para uso no repositório para refinamento de coordenadas atômicas, simplesmente definindo um hiperparâmetro structure_module_type .
se3 Transformador SE3
egnn EGNN
en E(n)-Transformador
De interesse para os leitores, cada uma das três estruturas também foi validada por pesquisadores em problemas relacionados.
$ python setup.py test Esta biblioteca usará o incrível trabalho de Jonathan King neste repositório. Obrigado Jonatas!
Também temos os dados MSA, todos com valor de aproximadamente 3,5 TB, baixados e hospedados pelo Archivist, dono do projeto The-Eye. (Eles também hospedam os dados e modelos para Eleuther AI) Considere uma doação se você achar que eles são úteis.
$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txthttps://xukui.cn/alphafold2.html
https://moalquraishi.wordpress.com/2020/12/08/alphafold2-casp14-it-feels-like-ones-child-has-left-home/

https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf
https://pubmed.ncbi.nlm.nih.gov/33637700/
Apresentação tFold, dos laboratórios Tencent AI
cd downloads_folder > pip install pyrosetta_wheel_filename.whlOpenMM Âmbar
@misc { unpublished2021alphafold2 ,
title = { Alphafold2 } ,
author = { John Jumper } ,
year = { 2020 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @article { Rao2021.02.12.430858 ,
author = { Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander } ,
title = { MSA Transformer } ,
year = { 2021 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858 } ,
journal = { bioRxiv }
} @article { Rives622803 ,
author = { Rives, Alexander and Goyal, Siddharth and Meier, Joshua and Guo, Demi and Ott, Myle and Zitnick, C. Lawrence and Ma, Jerry and Fergus, Rob } ,
title = { Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences } ,
year = { 2019 } ,
doi = { 10.1101/622803 } ,
publisher = { Cold Spring Harbor Laboratory } ,
journal = { bioRxiv }
} @article { Elnaggar2020.07.12.199554 ,
author = { Elnaggar, Ahmed and Heinzinger, Michael and Dallago, Christian and Rehawi, Ghalia and Wang, Yu and Jones, Llion and Gibbs, Tom and Feher, Tamas and Angerer, Christoph and Steinegger, Martin and BHOWMIK, DEBSINDHU and Rost, Burkhard } ,
title = { ProtTrans: Towards Cracking the Language of Life{textquoteright}s Code Through Self-Supervised Deep Learning and High Performance Computing } ,
elocation-id = { 2020.07.12.199554 } ,
year = { 2021 } ,
doi = { 10.1101/2020.07.12.199554 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554.full.pdf } ,
journal = { bioRxiv }
} @misc { king2020sidechainnet ,
title = { SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning } ,
author = { Jonathan E. King and David Ryan Koes } ,
year = { 2020 } ,
eprint = { 2010.08162 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { alquraishi2019proteinnet ,
title = { ProteinNet: a standardized data set for machine learning of protein structure } ,
author = { Mohammed AlQuraishi } ,
year = { 2019 } ,
eprint = { 1902.00249 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { gomez2017reversible ,
title = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
author = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
year = { 2017 } ,
eprint = { 1707.04585 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CV }
} @misc { fuchs2021iterative ,
title = { Iterative SE(3)-Transformers } ,
author = { Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner } ,
year = { 2021 } ,
eprint = { 2102.13419 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { satorras2021en ,
title = { E(n) Equivariant Graph Neural Networks } ,
author = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
year = { 2021 } ,
eprint = { 2102.09844 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { su2021roformer ,
title = { RoFormer: Enhanced Transformer with Rotary Position Embedding } ,
author = { Jianlin Su and Yu Lu and Shengfeng Pan and Bo Wen and Yunfeng Liu } ,
year = { 2021 } ,
eprint = { 2104.09864 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CL }
} @article { Gao_2020 ,
title = { Kronecker Attention Networks } ,
ISBN = { 9781450379984 } ,
url = { http://dx.doi.org/10.1145/3394486.3403065 } ,
DOI = { 10.1145/3394486.3403065 } ,
journal = { Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining } ,
publisher = { ACM } ,
author = { Gao, Hongyang and Wang, Zhengyang and Ji, Shuiwang } ,
year = { 2020 } ,
month = { Jul }
} @article { Si2021.05.10.443415 ,
author = { Si, Yunda and Yan, Chengfei } ,
title = { Improved protein contact prediction using dimensional hybrid residual networks and singularity enhanced loss function } ,
elocation-id = { 2021.05.10.443415 } ,
year = { 2021 } ,
doi = { 10.1101/2021.05.10.443415 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415.full.pdf } ,
journal = { bioRxiv }
} @article { Costa2021.06.02.446809 ,
author = { Costa, Allan and Ponnapati, Manvitha and Jacobson, Joseph M. and Chatterjee, Pranam } ,
title = { Distillation of MSA Embeddings to Folded Protein Structures with Graph Transformers } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.02.446809 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809.full.pdf } ,
journal = { bioRxiv }
} @article { Baek2021.06.14.448402 ,
author = { Baek, Minkyung and DiMaio, Frank and Anishchenko, Ivan and Dauparas, Justas and Ovchinnikov, Sergey and Lee, Gyu Rie and Wang, Jue and Cong, Qian and Kinch, Lisa N. and Schaeffer, R. Dustin and Mill{'a}n, Claudia and Park, Hahnbeom and Adams, Carson and Glassman, Caleb R. and DeGiovanni, Andy and Pereira, Jose H. and Rodrigues, Andria V. and van Dijk, Alberdina A. and Ebrecht, Ana C. and Opperman, Diederik J. and Sagmeister, Theo and Buhlheller, Christoph and Pavkov-Keller, Tea and Rathinaswamy, Manoj K and Dalwadi, Udit and Yip, Calvin K and Burke, John E and Garcia, K. Christopher and Grishin, Nick V. and Adams, Paul D. and Read, Randy J. and Baker, David } ,
title = { Accurate prediction of protein structures and interactions using a 3-track network } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.14.448402 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402.full.pdf } ,
journal = { bioRxiv }
}