@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}Você sabia que o neurodiffeq oferece suporte a pacotes de soluções e pode ser usado para resolver problemas reversos? Veja aqui!
? Já conhece o neurodiffeq? ? Vá para as perguntas frequentes.
neurodiffeq é um pacote para resolver equações diferenciais com redes neurais. Equações diferenciais são equações que relacionam alguma função com suas derivadas. Eles emergem em vários domínios científicos e de engenharia. Tradicionalmente, estes problemas podem ser resolvidos por métodos numéricos (por exemplo, diferença finita, elemento finito). Embora estes métodos sejam eficazes e adequados, a sua expressividade é limitada pela representação da sua função. Seria interessante se pudéssemos calcular soluções para equações diferenciais que fossem contínuas e diferenciáveis.
Como aproximadores de funções universais, as redes neurais artificiais demonstraram ter o potencial de resolver equações diferenciais ordinárias (EDOs) e equações diferenciais parciais (EDPs) com certas condições iniciais/de contorno. O objetivo do neurodiffeq é implementar essas técnicas existentes de uso de RNA para resolver equações diferenciais de uma forma que permita que o software seja flexível o suficiente para trabalhar em uma ampla gama de problemas definidos pelo usuário.
Como a maioria das bibliotecas padrão, neurodiffeq está hospedado no PyPI. Para instalar a versão estável mais recente,
pip install -U neurodiffeq # '-U' significa atualizar para a versão mais recente
Alternativamente, você pode instalar a biblioteca manualmente para obter acesso antecipado aos nossos novos recursos. Esta é a forma recomendada para desenvolvedores que desejam contribuir com a biblioteca.
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && pip install -r requisitos instalação do pip. # Para fazer alterações na biblioteca, use `pip install -e .`pytest testes/ # Execute testes. Opcional.
Ficaremos felizes em ajudá-lo com qualquer dúvida. Enquanto isso, você pode conferir as perguntas frequentes.
Para visualizar tutoriais completos e documentação do neurodiffeq , verifique a documentação oficial.
Além das documentações, fizemos recentemente um rápido vídeo de demonstração com slides.
de neurodiffeq importar diff de neurodiffeq.solvers importar Solver1D, Solver2D de neurodiffeq.conditions importar IVP, DirichletBVP2D de neurodiffeq.networks importar FCNN, SinActv
Aqui resolvemos um sistema não linear de duas EDOs, conhecido como equações de Lotka-Volterra. Existem duas funções desconhecidas ( u e v ) e uma única variável independente ( t ).
def ode_system(u, v, t): retorno [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]condições = [IVP(t_0=0,0, u_0=1,5 ), IVP(t_0=0,0, u_0=1,0)]redes = [FCNN(actv=SinActv), FCNN(actv=SinActv)]solver = Solver1D(ode_system, condições, t_min=0,1, t_max=12,0, nets=nets)solver.fit(max_epochs=3000)solução = solucionador.get_solution()
solution é um objeto que pode ser chamado, você pode passar matrizes numpy ou tensores de tocha para ele como
u, v = solução(t, to_numpy=True) # t pode ser np.ndarray ou torch.Tensor
Traçar u e v em relação às suas soluções analíticas resulta em algo como:
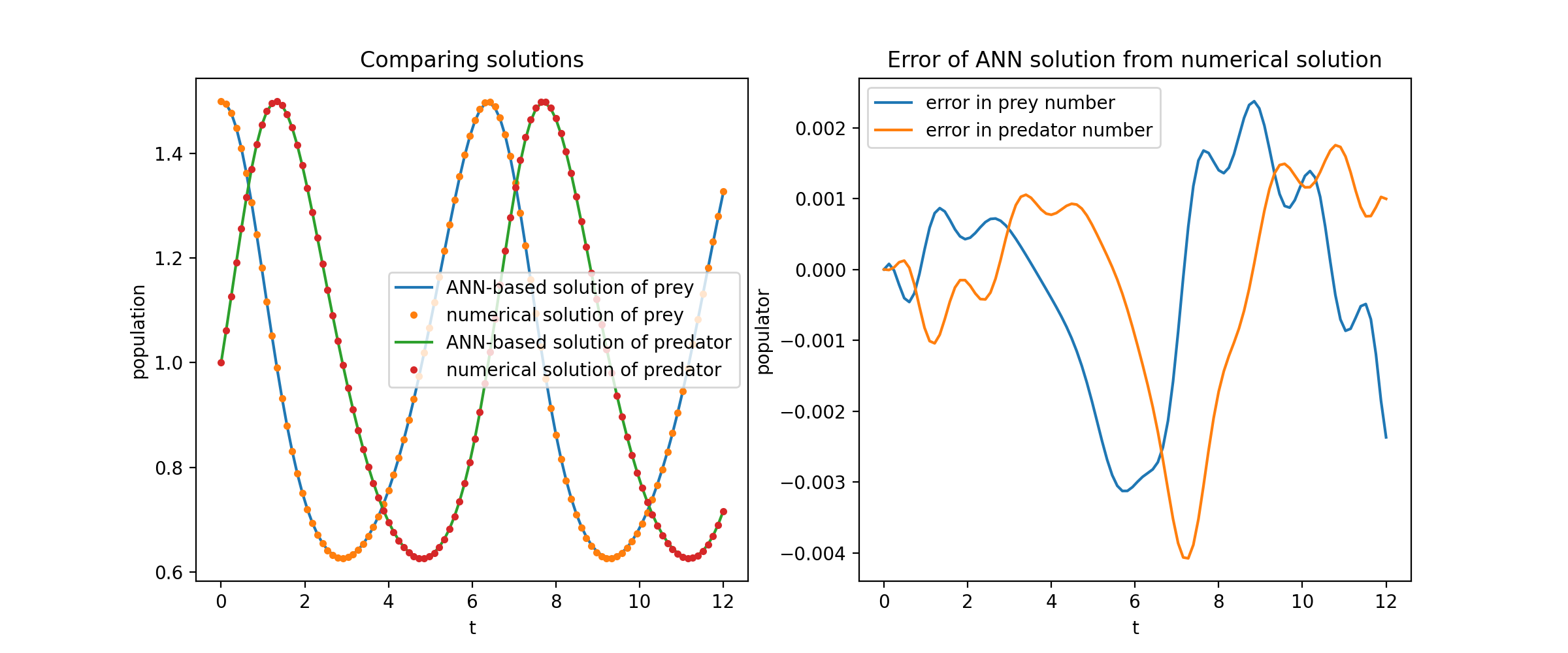
Aqui resolvemos uma equação de Laplace com condições de contorno de Dirichlet em um retângulo. Observe que escolhemos a equação de Laplace por sua simplicidade de cálculo da solução analítica. Na prática, você pode tentar qualquer PDE caótico e não linear , desde que ajuste o solucionador bem o suficiente.
Resolver um sistema EDP 2-D é bastante semelhante a resolver EDOs, exceto que existem duas variáveis x e y para problemas de valor de contorno ou x e t para problemas de valor de contorno inicial, sendo que ambas são suportadas.
def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]condições = [DirichletBVP2D(x_min=0, x_min_val=lambda y: tocha. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=lambda x: 0, y_max=1, y_max_val=lambda x: 0,
)
]redes = [FCNN(n_input_units=2, n_output_units=1, hidden_units=(512,))]solver = Solver2D(pde_system, condições, xy_min=(0, 0), xy_max=(1, 1), redes=redes) solucionador.fit(max_epochs=2000)solução = solucionador.get_solution() A assinatura da solution para uma EDP 2D é ligeiramente diferente daquela de uma EDO. Novamente, ele aceita matrizes numpy ou tensores de tocha.
você = solução (x, y, to_numpy=True)
Avaliar u em [0,1] × [0,1] produz os seguintes gráficos
| Solução baseada em RNA | Resíduo de PDE |
|---|---|
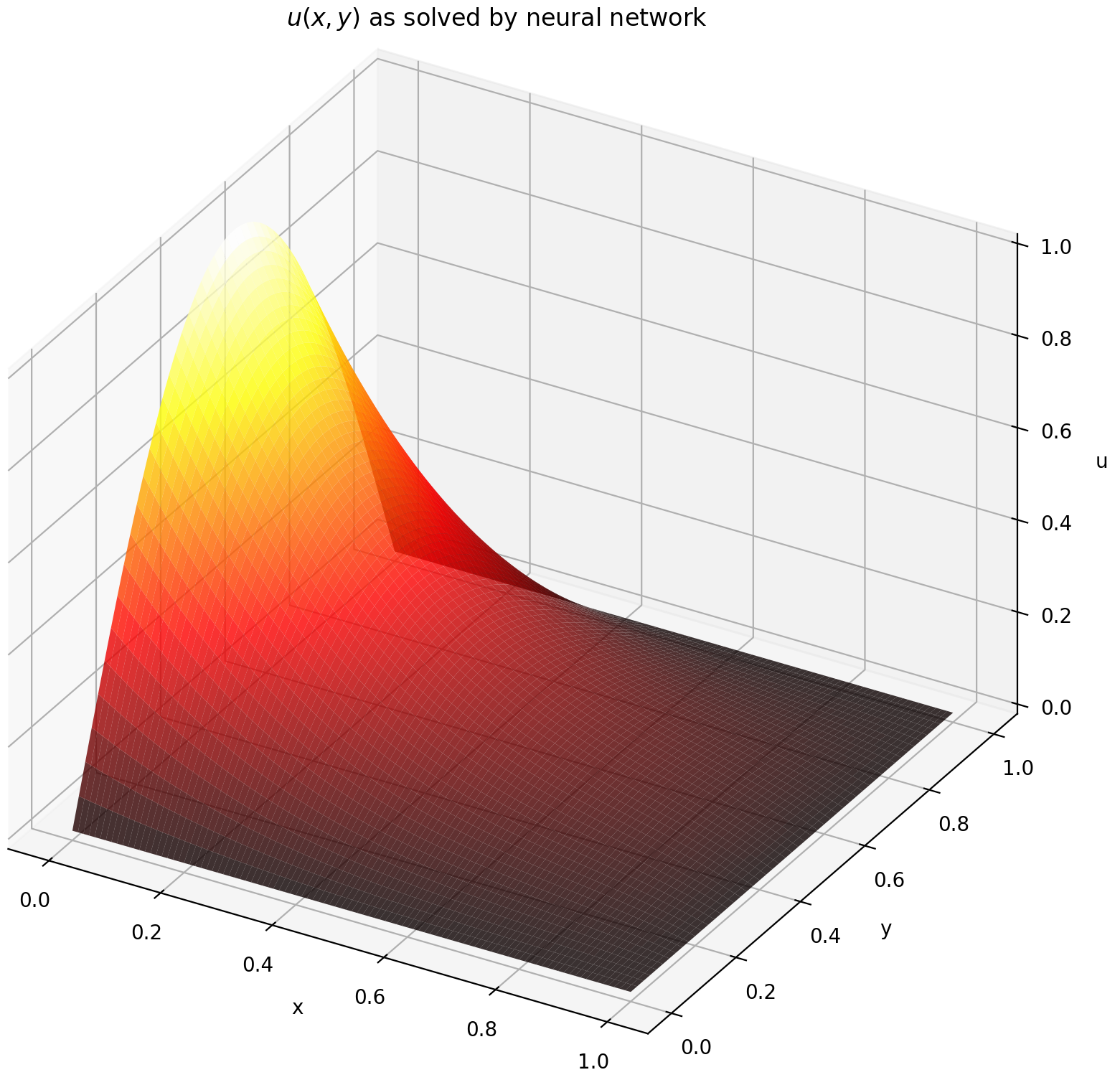 | 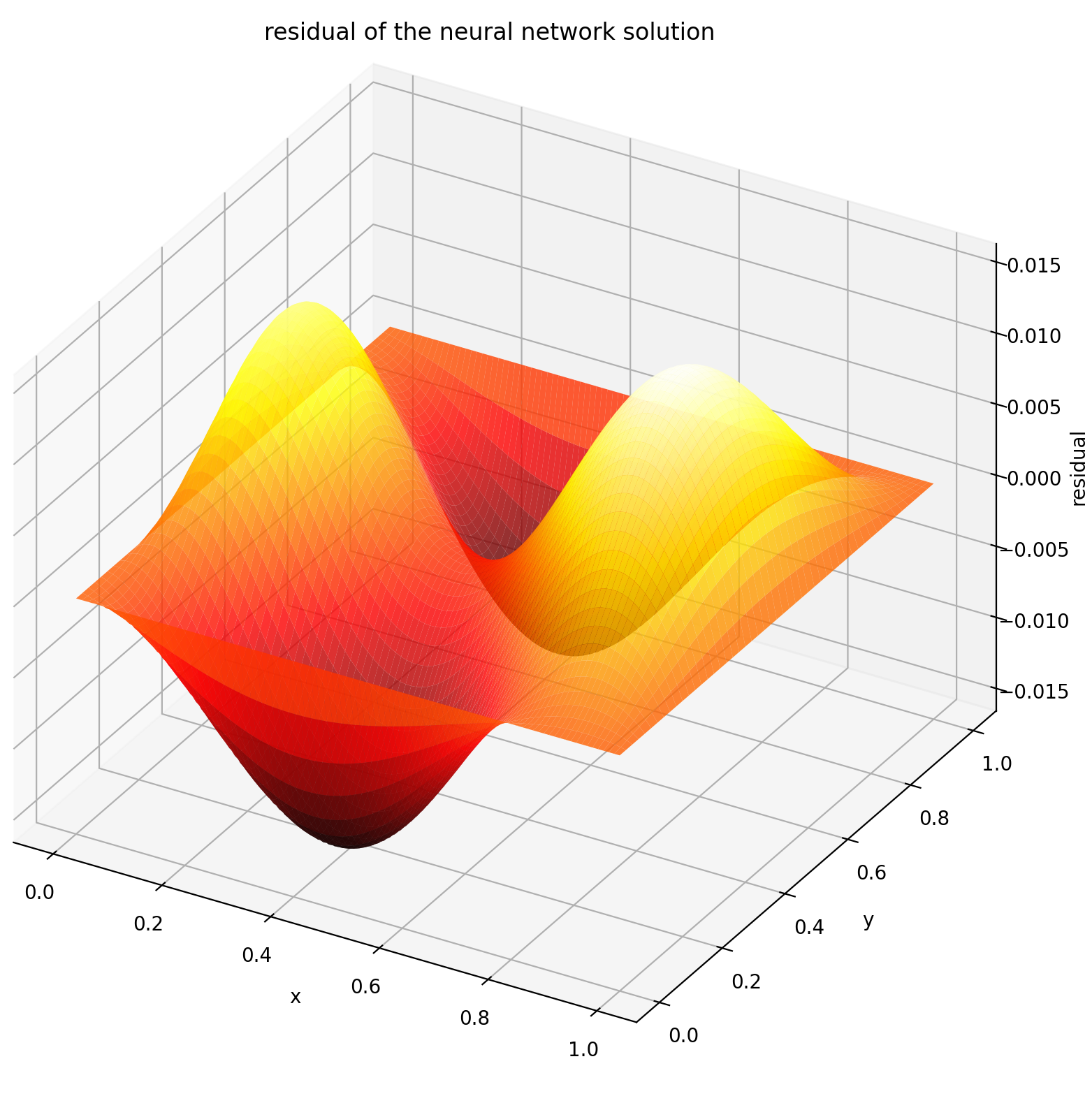 |
Um monitor é uma ferramenta para visualizar soluções PDE/ODE, bem como histórico de perdas e métricas personalizadas durante o treinamento. Os usuários do Jupyter Notebooks precisam executar a mágica %matplotlib notebook . Para usuários do Jupyter Lab, experimente %matplotlib widget .
de neurodiffeq.monitors importar Monitor1D...monitor = Monitor1D(t_min=0,0, t_max=12,0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
Você deve ver os gráficos atualizados a cada 100 épocas, bem como na última época , mostrando dois gráficos - um para visualização da solução no intervalo [0,12] e outro para histórico de perdas (treinamento e validação).
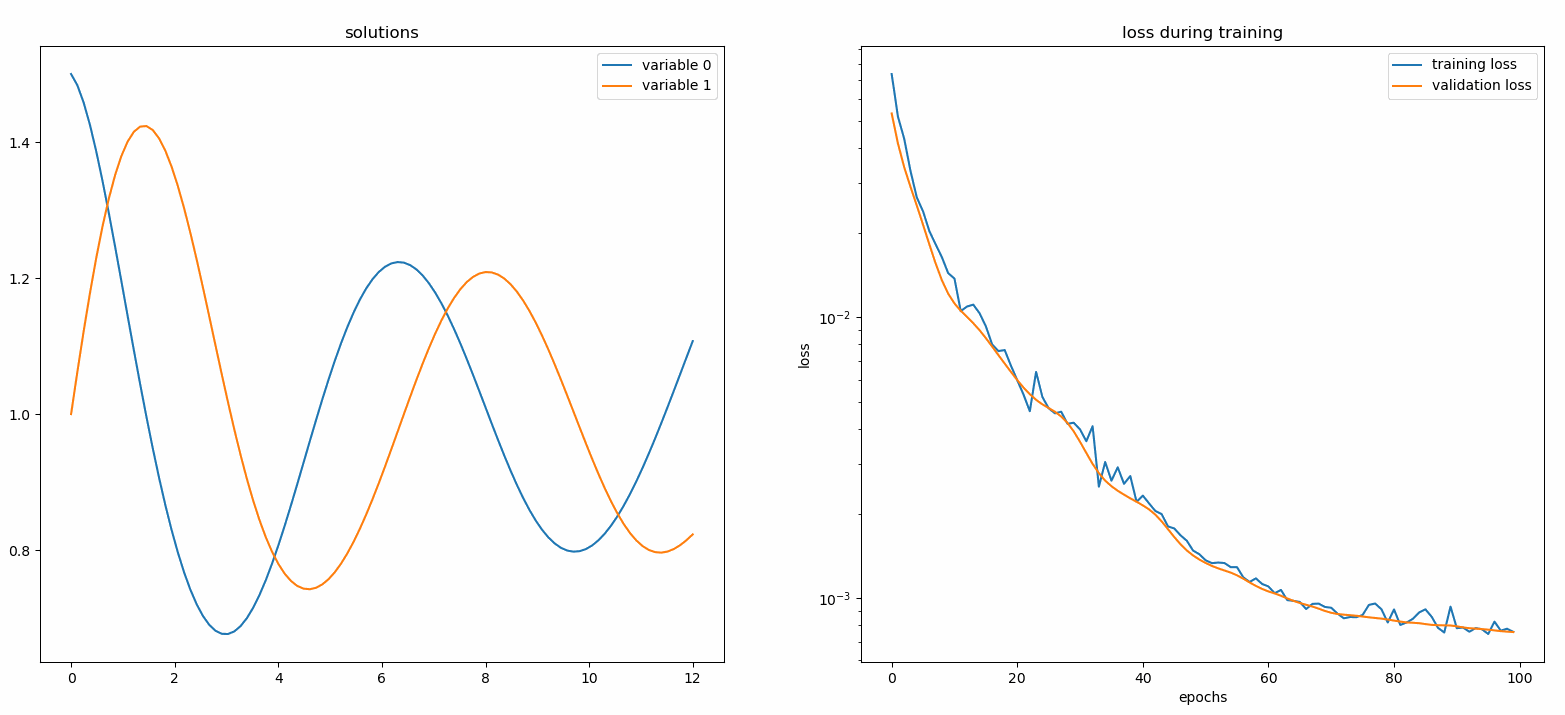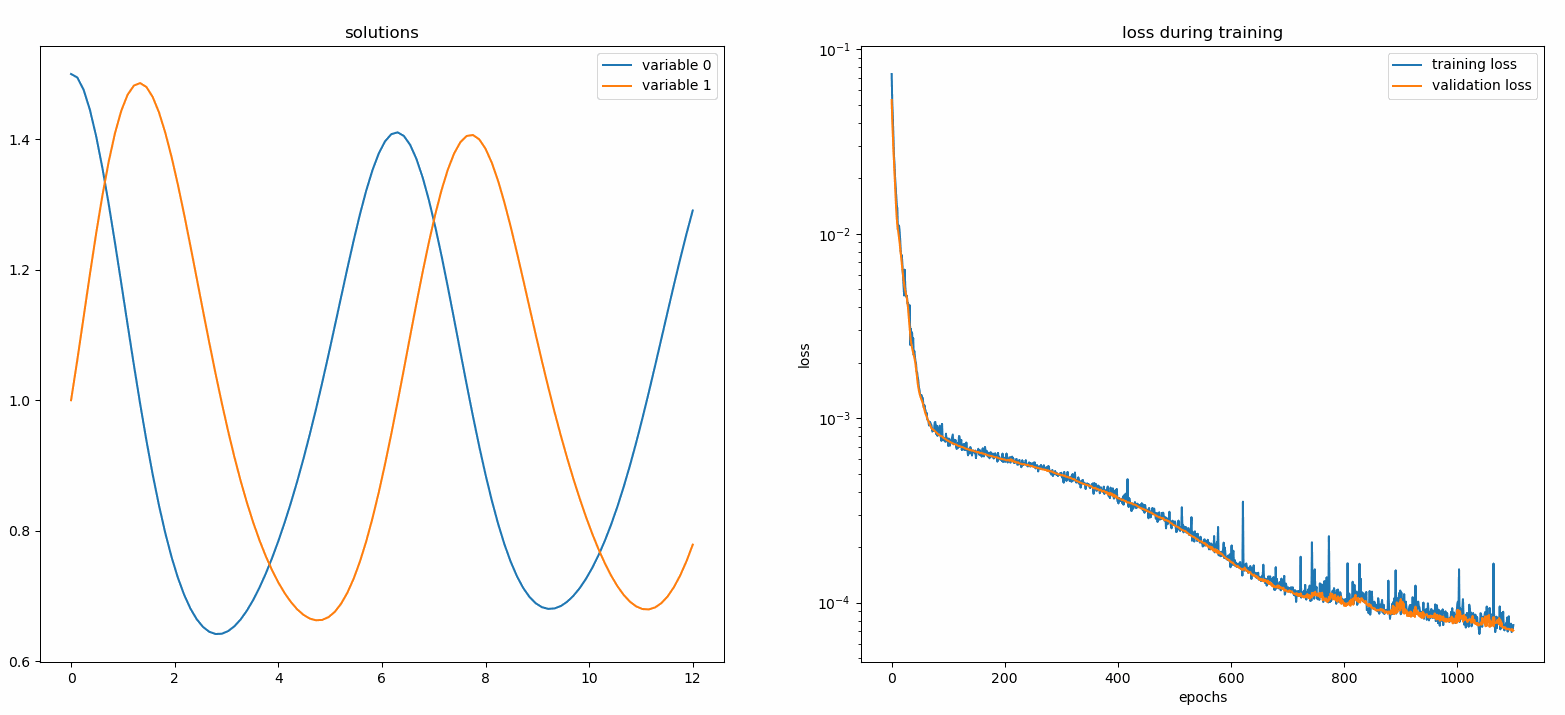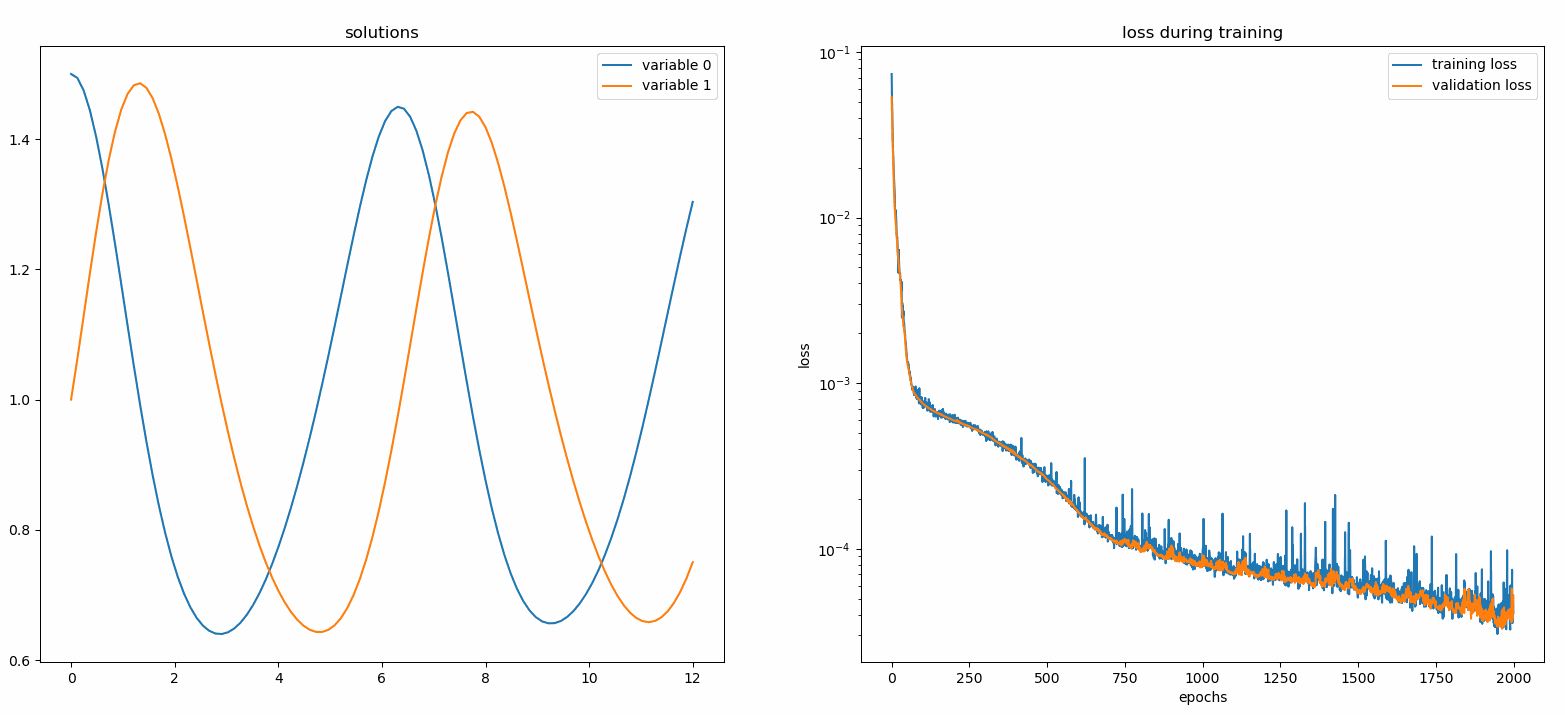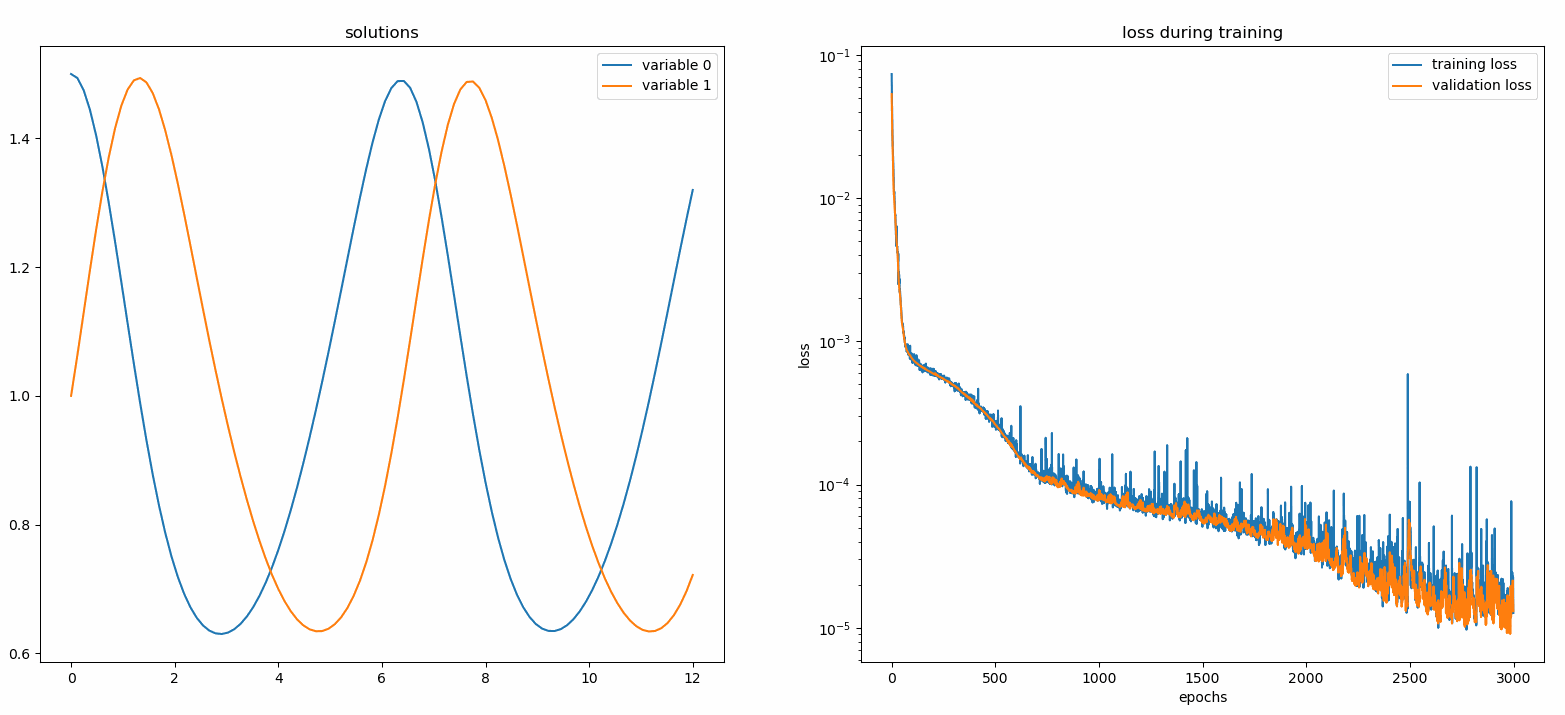
Por conveniência, implementamos uma FCNN – rede neural totalmente conectada, cujas unidades ocultas e funções de ativação podem ser customizadas.
de neurodiffeq.networks import FCNN# Padrão: n_input_units=1, n_output_units=1, hidden_units=[32, 32], ativação=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., hidden_units=[ ..., ..., ...], ativação=...) ...redes = [rede1, rede2, ...]
FCNN geralmente é um bom ponto de partida. Para usuários avançados, os solucionadores são compatíveis com qualquer torch.nn.Module personalizado. As únicas restrições são:
Os módulos recebem um tensor de forma (None, n_coords) e geram um tensor de forma (None, 1) .
Deve haver um total de módulos n_funcs nas nets a serem passados para solver = Solver(..., nets=nets) .
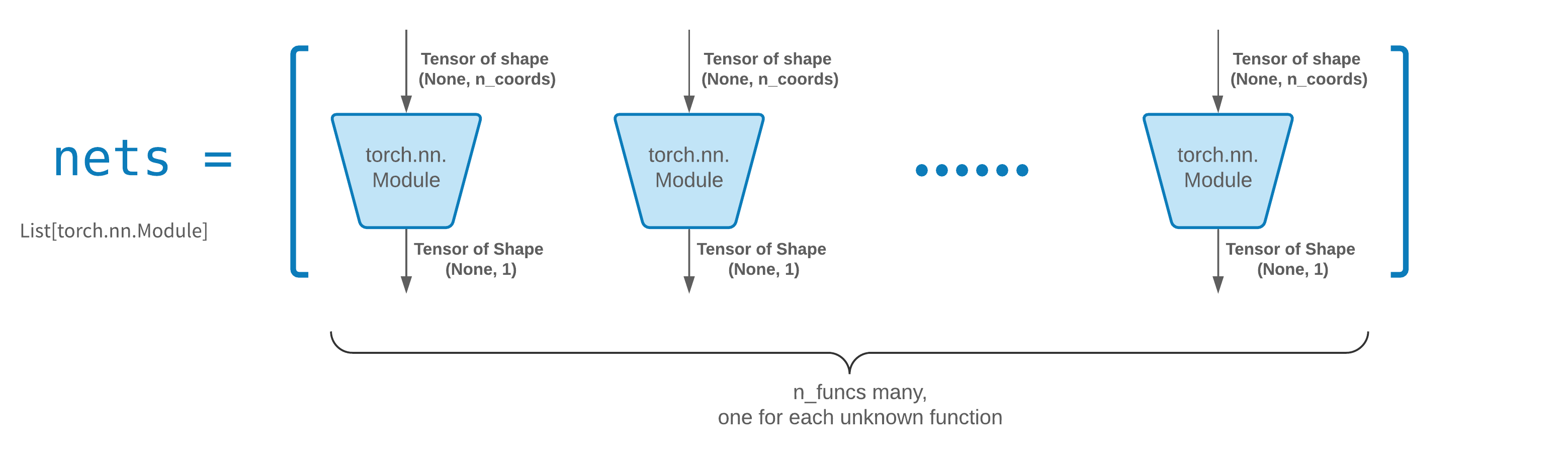
Na verdade, neurodiffeq possui um recurso single_net que não obedece às regras acima, que não serão abordadas aqui.
Leia o tutorial do PyTorch sobre como construir sua própria arquitetura de rede (também conhecida como módulo).
O aprendizado por transferência é feito facilmente serializando old_solver.nets (uma lista de módulos torch) para o disco e depois carregando-os e passando para um novo solucionador:
old_solver.fit(max_epochs=...)# ... despeja `old_solver.nets` no disco# ... carrega as redes do disco, armazena-as em alguma variável `loaded_nets` new_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_épocas=...)
Atualmente estamos trabalhando em funções wrapper para salvar/carregar redes e outras variáveis internas dos Solvers. Enquanto isso, você pode ler o tutorial do PyTorch sobre como salvar e carregar suas redes.
No neurodiffeq, as redes são treinadas minimizando perdas (resíduos de EDO/PDE) avaliadas em um conjunto de pontos do domínio. Os pontos são reamostrados aleatoriamente todas as vezes. Para controlar o número, a distribuição e o domínio delimitador dos pontos amostrados, você pode especificar seus próprios generator de treinamento/valiação.
de neurodiffeq.generators import Generator1D# Padrão t_min=0,0, t_max=1,0, method='uniform', noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. ., noise_std=...)g2 = Gerador1D(tamanho=..., t_min=..., t_max=..., método=..., noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
Aqui estão alguns exemplos de distribuições de um Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
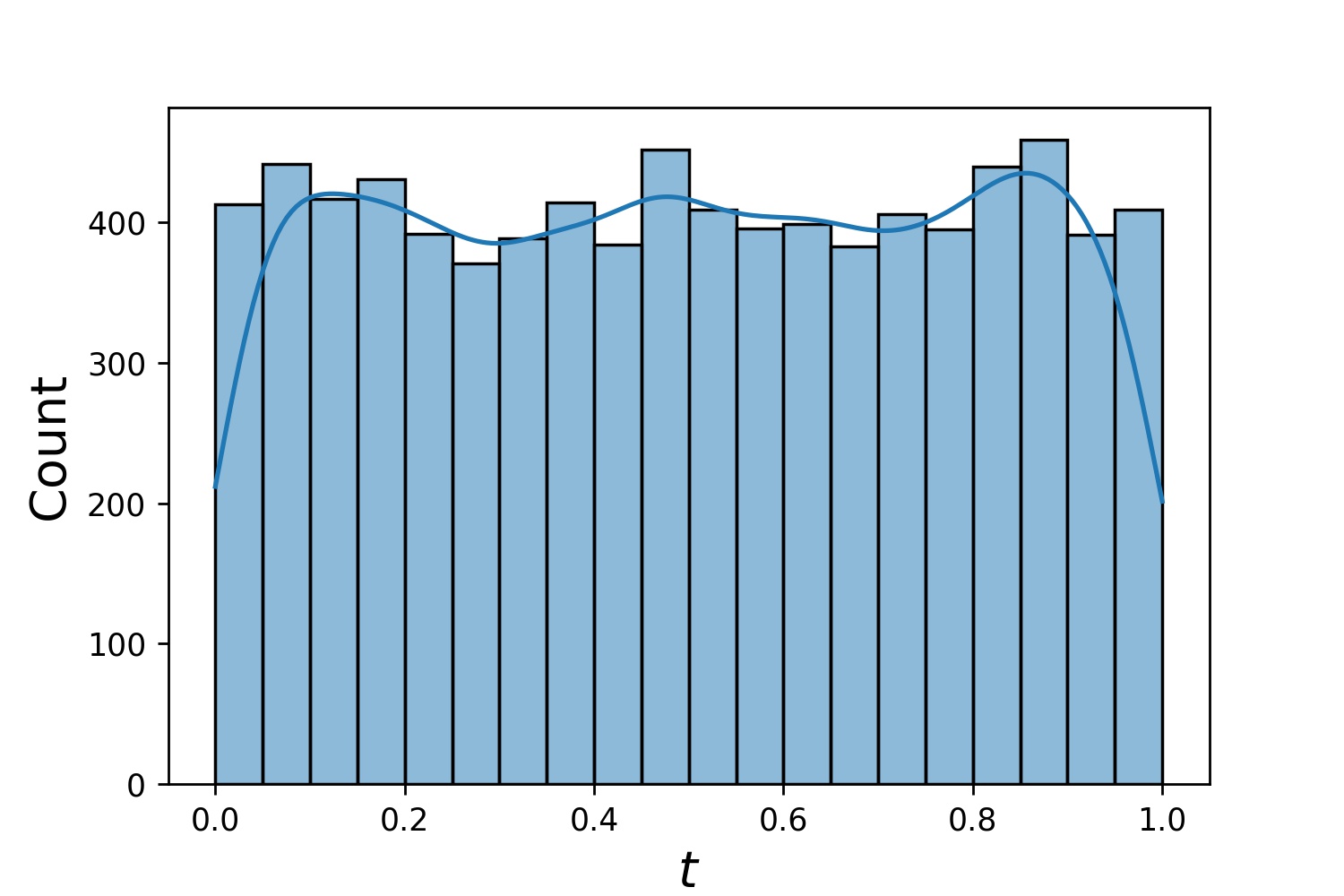 | 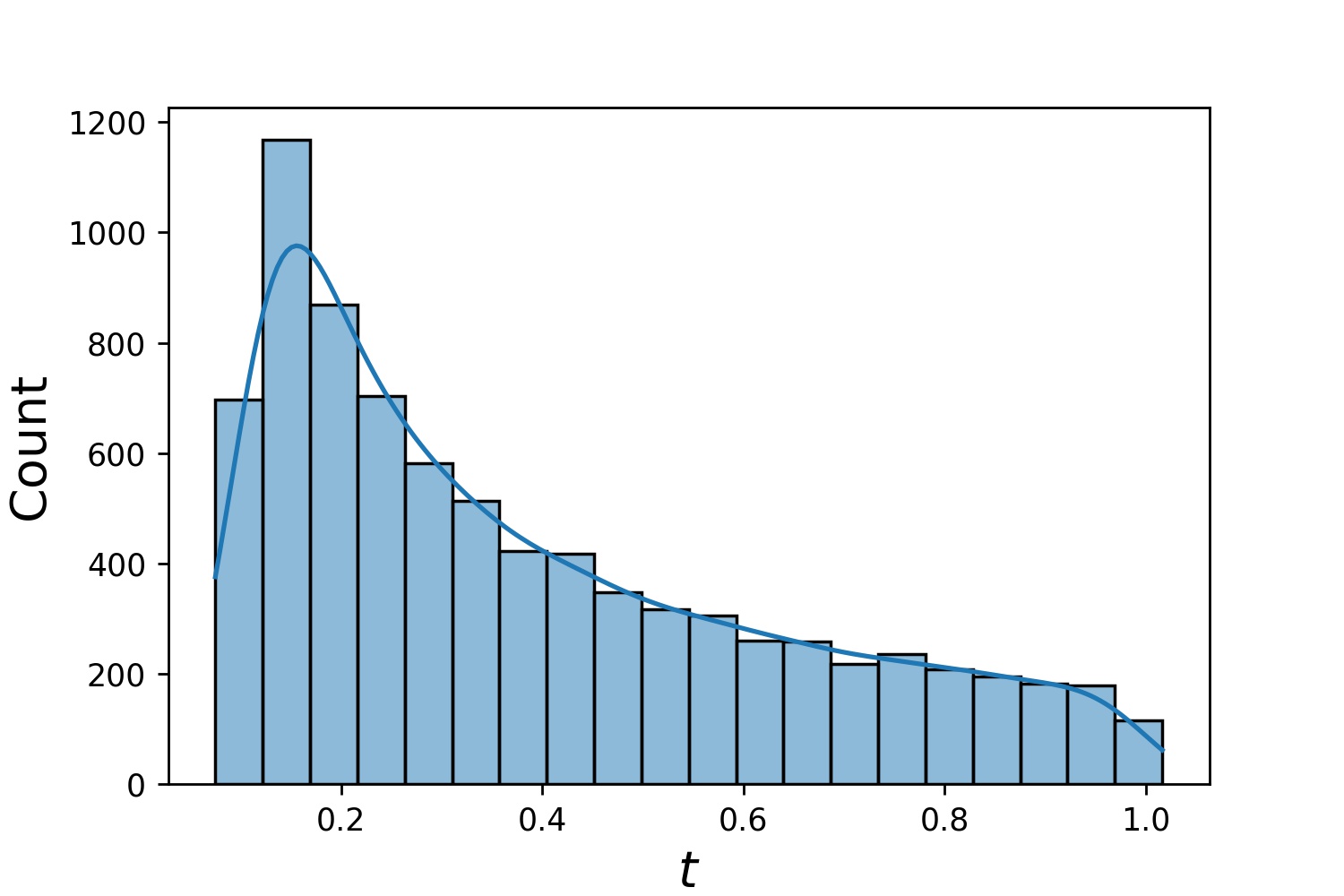 |
Observe que quando train_generator e valid_generator são especificados, t_min e t_max podem ser omitidos em Solver1D(...) . Na verdade, mesmo se você passar t_min , t_max , train_generator , valid_generator juntos, t_min e t_max ainda serão ignorados.
Outra característica interessante dos geradores é que você pode concatená-los, por exemplo
g1 = Gerador2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Gerador2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))g = g1 + g2
Aqui, g será um gerador que produz as amostras combinadas de g1 e g2
g1 | g2 | g1 + g2 |
|---|---|---|
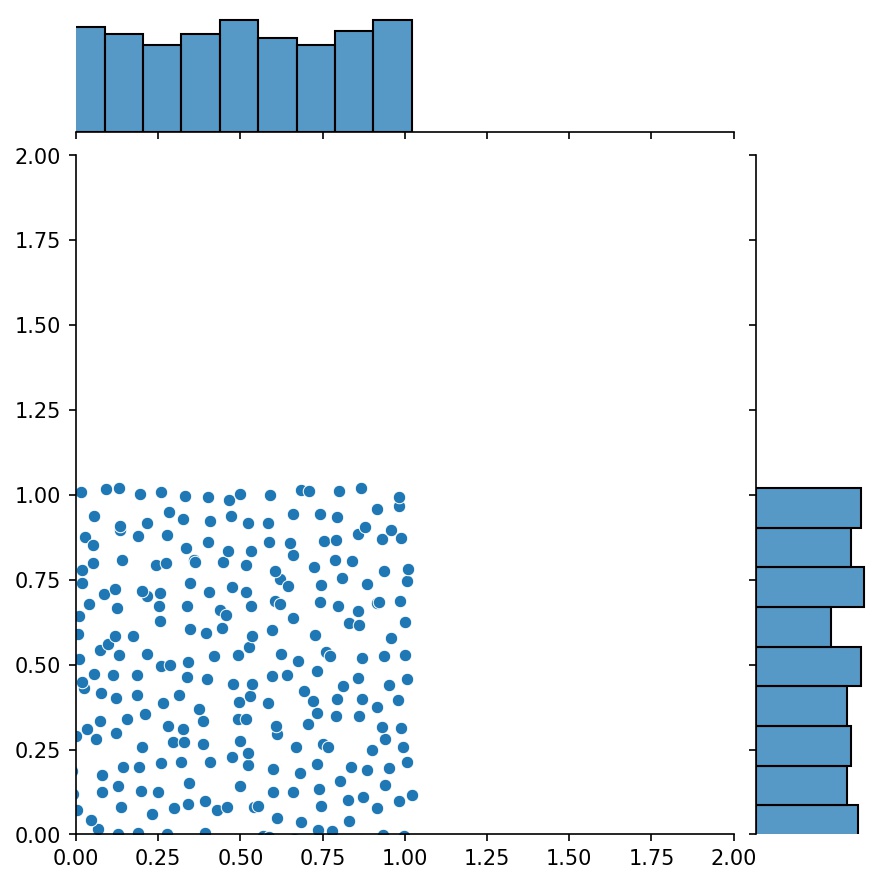 | 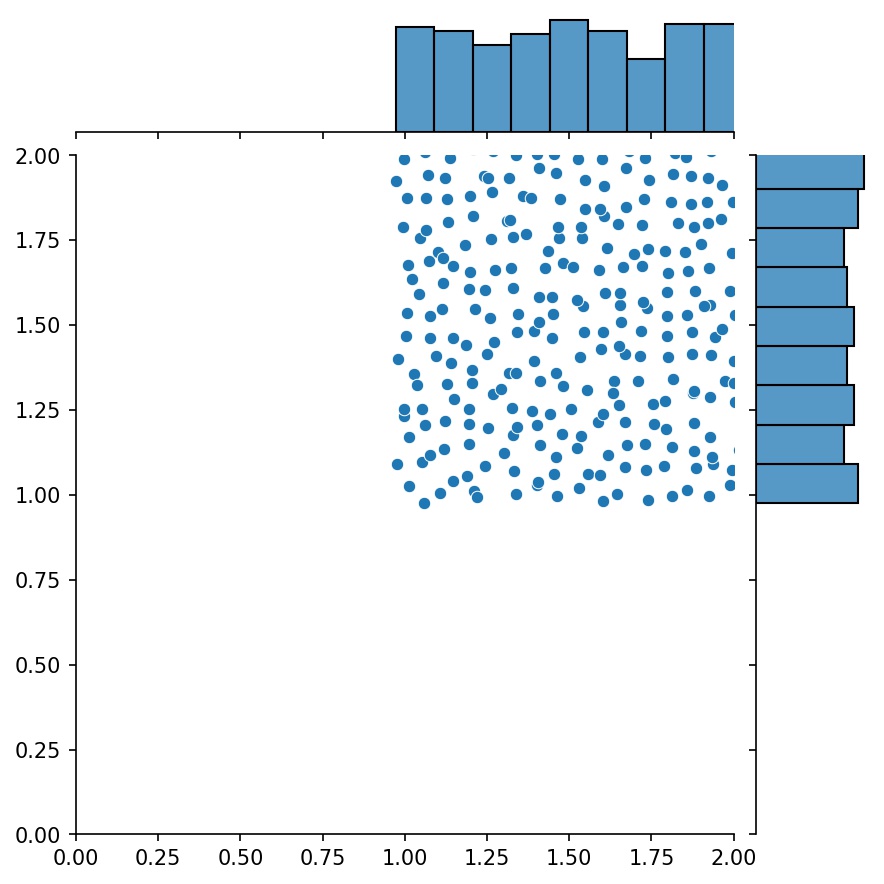 |  |
Você pode usar Generator2D , Generator3D , etc. para pontos de amostragem em dimensões superiores. Mas também há outra maneira
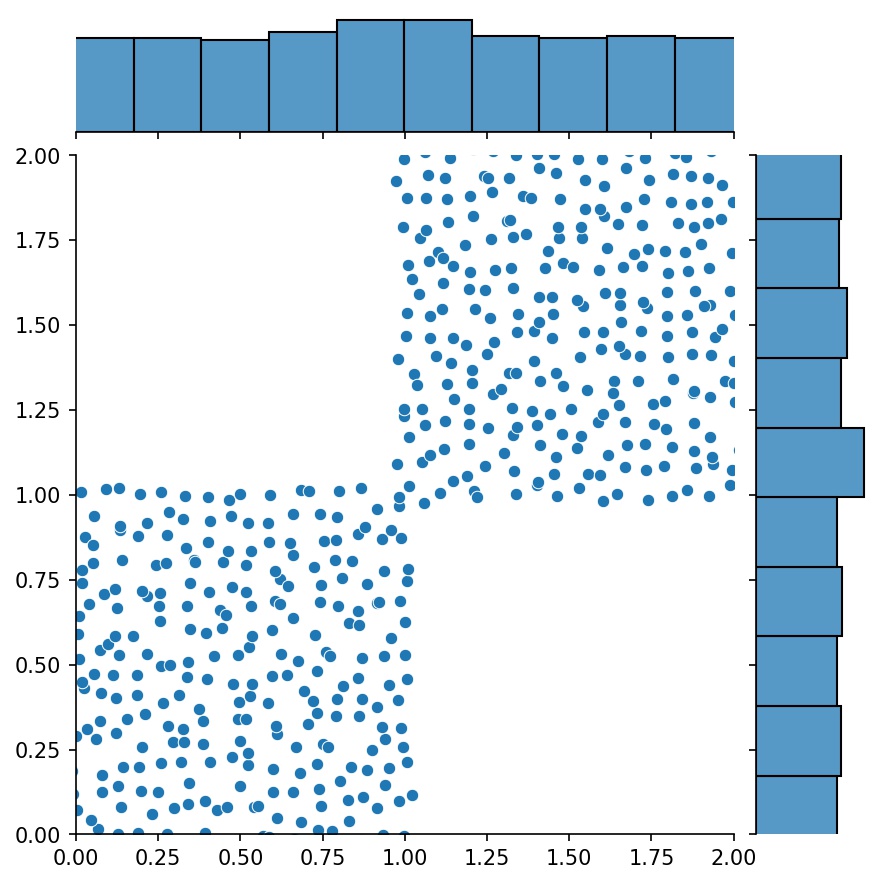
g1 = Gerador1D(1024, 2,0, 3,0, método='uniform')g2 = Gerador1D(1024, 0,1, 1,0, método='log-spaced-noisy', noise_std=0,001)g = g1 * g2
Aqui, g será um gerador que produz 1024 pontos em um retângulo 2-D (2,3) × (0.1,1) todas as vezes. As coordenadas x deles são extraídas de (2,3) usando a estratégia uniform e a coordenada y extraída de (0.1,1) usando a estratégia log-spaced-noisy .
g1 | g2 | g1 * g2 |
|---|---|---|
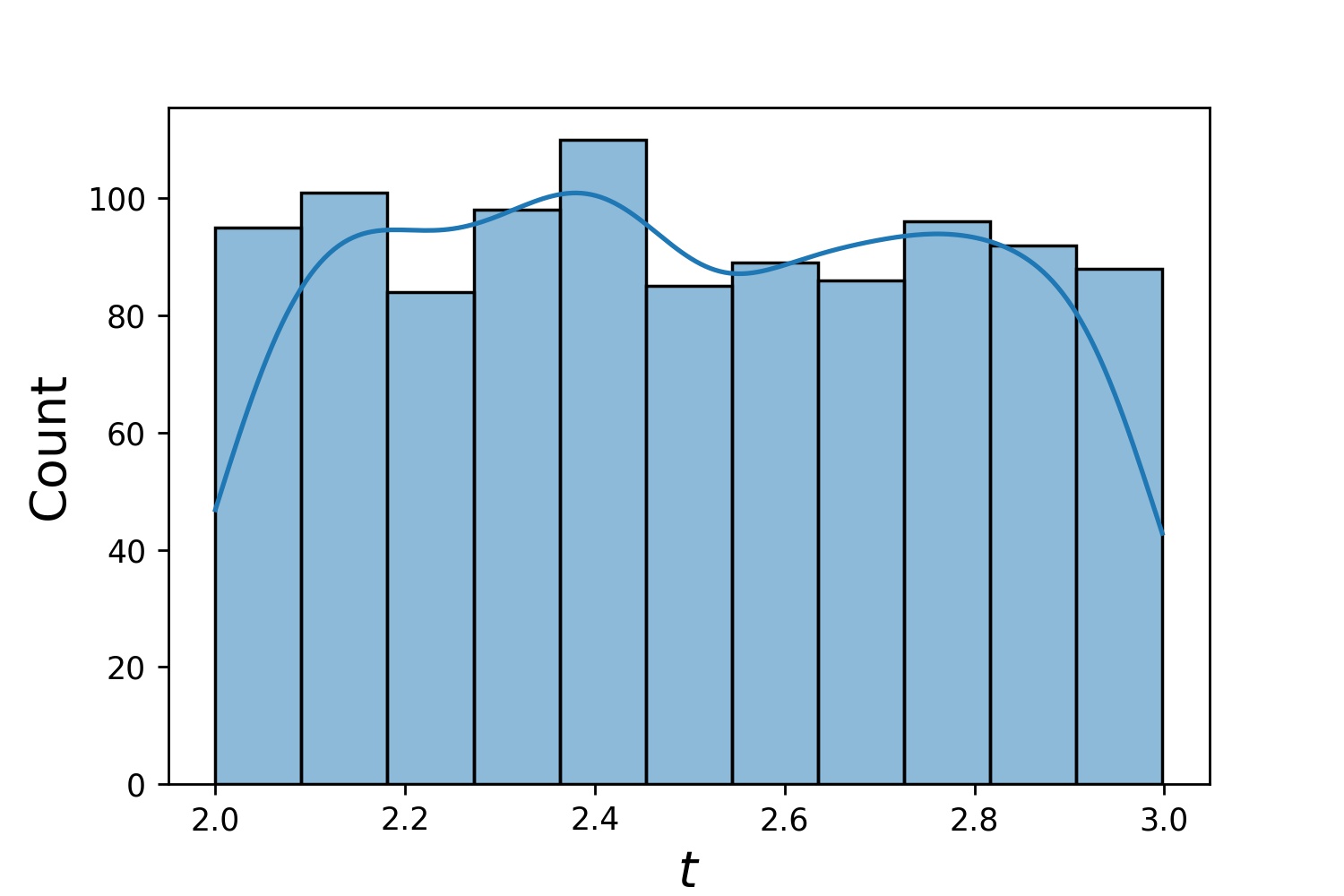 | 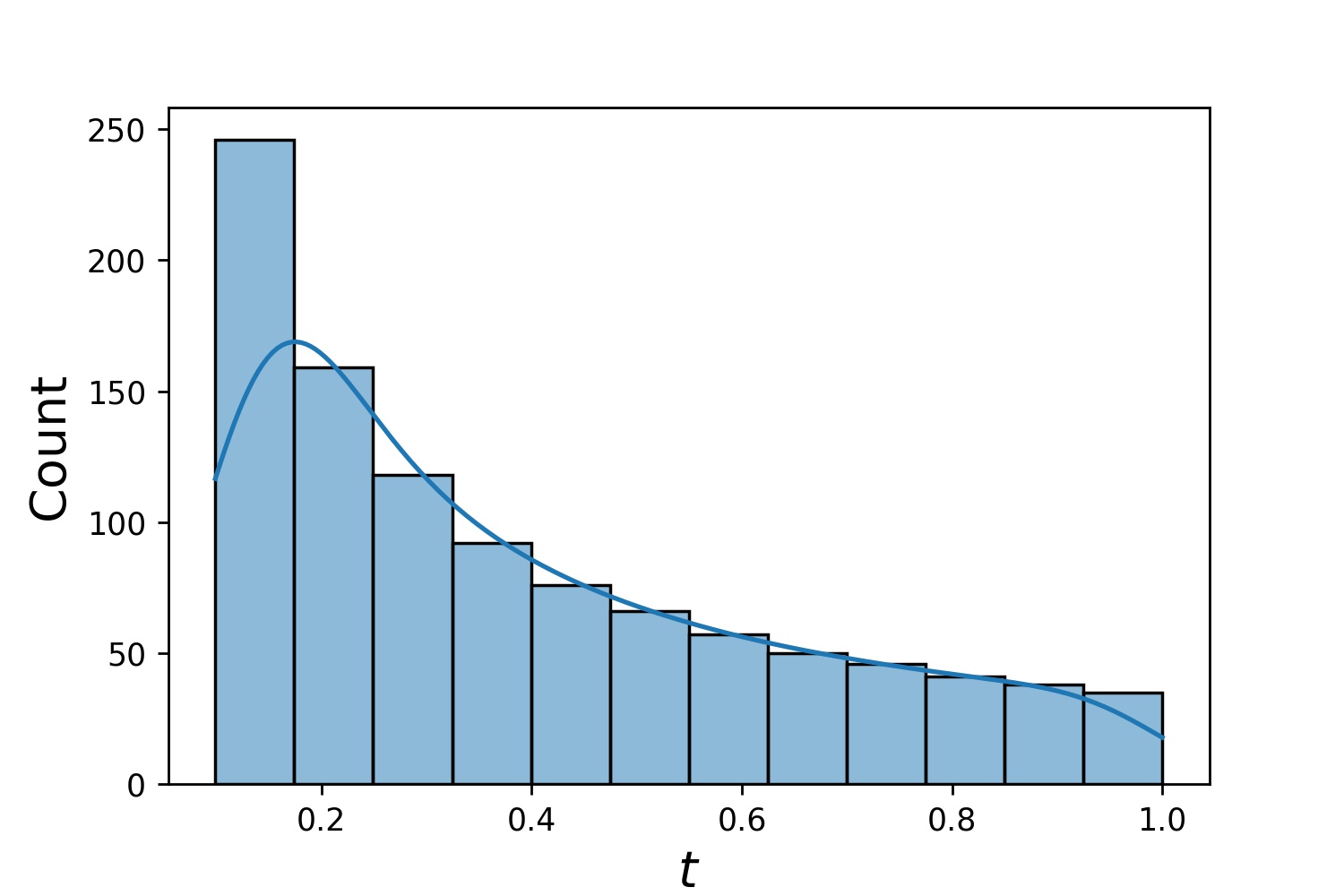 | 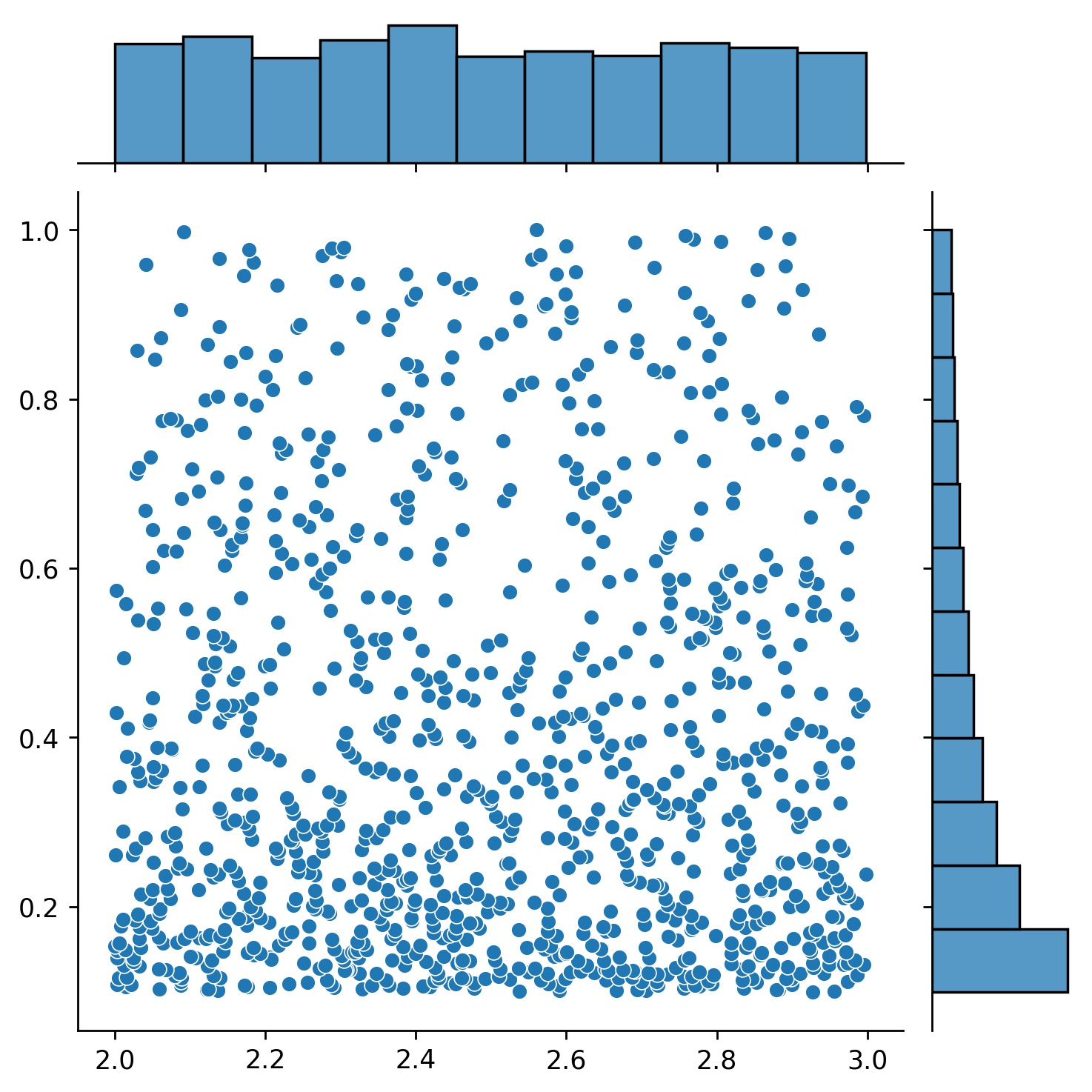 |
Às vezes, é interessante resolver um conjunto de equações de uma só vez. Por exemplo, você pode querer resolver equações diferenciais da forma du/dt + λu = 0 sob a condição inicial u(0) = U0 . Você pode querer resolver isso para todos λ e U0 de uma só vez, tratando-os como entradas para as redes neurais.
Uma dessas aplicações é para reações químicas, onde a taxa de reação é desconhecida. Diferentes taxas de reação correspondem a diferentes soluções e apenas uma solução corresponde aos pontos de dados observados. Talvez você esteja interessado em primeiro resolver um conjunto de soluções e depois determinar as melhores taxas de reação (também conhecidas como parâmetros da equação). A segunda etapa é conhecida como problema inverso .
Aqui está um exemplo de como fazer isso usando neurodiffeq :
Digamos que temos uma equação du/dt + λu = 0 e condição inicial u(0) = U0 onde λ e U0 são constantes desconhecidas. Também temos um conjunto de observações t_obs e u_obs . Primeiro importamos BundleSolver e BundleIVP que são necessários para obter um pacote de soluções:
de neurodiffeq.conditions import BundleIVPfrom neurodiffeq.solvers import BundleSolver1Dimport matplotlib.pyplot as pltimport numpy as npimport torchfrom neurodiffeq import diff
Determinamos o domínio da entrada t , bem como o domínio dos parâmetros λ e U0 . Também precisamos tomar uma decisão sobre a ordem dos parâmetros. Ou seja, qual deve ser o primeiro parâmetro e qual deve ser o segundo. Para efeitos desta demonstração, escolhemos λ como o primeiro parâmetro (índice 0) e U0 como o segundo (índice 1). É muito importante acompanhar os índices dos parâmetros.
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # primeiro parâmetro, índice = 0U0_MIN, U0_MAX = 0,2, 0,6 # segundo parâmetro, índice = 1
Em seguida, definimos as conditions e solver como de costume, exceto que usamos BundleIVP e BundleSolver1D em vez de IVP e Solver1D . A interface desses dois é muito semelhante ao IVP e Solver1D . Você pode descobrir mais na referência da API.
# os parâmetros da equação vêm após as entradas (geralmente coordenadas temporais e espaciais)diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# O argumento da palavra-chave deve ser nomeado "u_0" no BundleIVP. Se você usar qualquer outra coisa, por exemplo `y0`, `u0`, etc., não funcionará.conditions = [BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1}) # u_0 has índice 1]solucionador = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ tem índice 0; u_0 tem índice 1theta_max=[LAMBDA_MAX, U0_MAX], # λ tem índice 0; u_0 tem índice 1eq_param_index=(0,), # λ é o único parâmetro da equação, que possui índice 0n_batches_valid=1,
) Como λ é um parâmetro na equação e U0 é um parâmetro na condição inicial , devemos incluir λ no diff_eq e U0 na condição. Se um parâmetro estiver presente tanto na equação quanto na condição, ele deverá ser incluído em ambos os locais. Todos os elementos de conditions passados para BundleSovler1D devem ser condições Bundle* , mesmo que não tenham parâmetros.
Agora podemos treiná-lo e obter a solução como faríamos normalmente.
solucionador.fit(max_epochs=1000)solução = solucionador.get_solution(melhor=Verdadeiro)
A solução espera três entradas – t , λ e U0 . Todas as entradas devem ter o mesmo formato. Por exemplo, se você estiver interessado em fixar λ=4 e U0=0.4 e traçar a solução u contra t ∈ [0,1] , você pode fazer o seguinte
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0,4 * np.ones_like(t)u = solução(t, lmd, u0, to_numpy=True)importar matplotlib.pyplot como pltplt .plot(t, você)
Depois de ter uma solution agrupada, você pode encontrar um conjunto de parâmetros (λ, U0) que corresponda mais de perto aos pontos de dados observados (t_i, u_i) . Isto é conseguido usando descida gradiente simples. No exemplo de brinquedo a seguir, presumimos que existem apenas três pontos de dados u(0.2) = 0.273 , u(0.5)=0.129 e u(0.8) = 0.0609 . A seguir está o fluxo de trabalho clássico do PyTorch.
# pontos de dados observadost_obs = torch.tensor([0,2, 0,5, 0,8]).reshape(-1, 1)u_obs = torch.tensor([0,273, 0,129, 0,0609]).reshape(-1, 1)# inicialização aleatória de λ e U0; acompanhe seu gradientelmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(Verdadeiro)], lr = 1e-2) # execute a descida gradiente por 10.000 épocas para _ no intervalo (10.000): saída = solução (t_obs, lmd_tensor * torch.ones_like (t_obs), u0_tensor * torch.ones_like (t_obs)) perda = ((saída - você_obs) ** 2).mean()perda.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, perda = {loss.item()}") Simples. Ao importar o neurodiffeq, a biblioteca detecta automaticamente se CUDA está disponível em sua máquina. Como a biblioteca é baseada em PyTorch, ela definirá o tipo de tensor padrão como torch.cuda.DoubleTensor se um dispositivo GPU compatível for encontrado.
Consulte as seções Redes Personalizadas e Aprendizagem por Transferência.
A maneira padrão do PyTorch.
Construa suas redes conforme explicado em Redes Personalizadas: nets = [FCNN(), FCN(), ...]
Instancie um otimizador customizado e passe todos os parâmetros dessas redes para ele
parâmetros = [p for net in nets for p in net.parameters()] # lista de parâmetros de todas as redesMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
Passe AMBAS suas nets e seu optimizer para o solucionador: solver = Solver1D(..., nets=nets, optimizer=optimizer)
Ao contrário dos métodos numéricos tradicionais (FEM, FVM, etc.), a solução baseada em NN requer algum hiperajuste. A biblioteca oferece a máxima flexibilidade para testar qualquer combinação de hiperparâmetros.
Para usar uma arquitetura de rede diferente, você pode passar seus torch.nn.Module s personalizados.
Para usar um otimizador diferente, você pode passar seu próprio otimizador para solver = Solver(..., optimizer=my_optim) .
Para usar uma distribuição de amostragem diferente, você pode usar geradores integrados ou escrever seus próprios geradores do zero.
Para usar um tamanho de amostragem diferente, você pode ajustar os geradores ou alterar solver = Solver(..., n_batches_train) .
Para alterar hiperparâmetros dinamicamente durante o treinamento, confira nosso recurso de retornos de chamada.
Não use ReLU para ativação, porque sua derivada de segunda ordem é idêntica a 0.
Redimensione seu PDE/ODE em formato adimensional, de preferência faça tudo variar em [0,1] . Trabalhar com um domínio como [0,1000000] está sujeito a falhas porque a) o PyTorch inicializa os pesos dos módulos para serem relativamente pequenos eb) a maioria das funções de ativação (como Sigmoid, Tanh, Swish) são mais não lineares perto de 0.
Se o seu PDE/ODE for muito complicado, considere tentar a aprendizagem curricular. Comece a treinar suas redes em um domínio menor e depois expanda gradualmente até que todo o domínio seja coberto.
Todos são bem-vindos para contribuir com este projeto.
Ao contribuir para este repositório, consideramos o seguinte processo:
Abra uma edição para discutir a mudança que você está planejando fazer.
Consulte as Diretrizes de Contribuição.
Faça a alteração em um repositório bifurcado e atualize o README.md se forem feitas alterações na interface.
Abra uma solicitação pull.