ai simplest network
1.0.0
Esta é a rede neural artificial mais simples possível explicada e demonstrada.
As redes neurais artificiais são inspiradas no cérebro por terem neurônios artificiais interconectados que armazenam padrões e se comunicam entre si. A forma mais simples de um neurônio artificial possui uma ou múltiplas entradas 
cada um com um peso específico 
e uma saída 
.
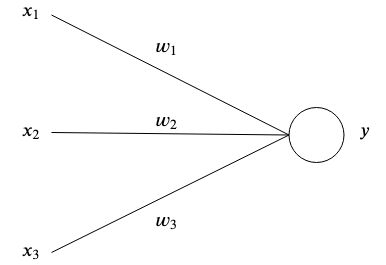
No nível mais simples, a saída é a soma de suas entradas vezes seus pesos.
O objetivo de uma rede é aprender uma determinada saída dada(s) determinada(s) entrada(s) 
aproximando uma função complexa com muitos parâmetros 
que não poderíamos inventar nós mesmos.
Digamos que temos uma rede com duas entradas 
e 
e dois pesos 
e 
.
A ideia é ajustar os pesos de forma que os insumos fornecidos produzam o resultado desejado.
Os pesos normalmente são inicializados aleatoriamente, pois não podemos saber seu valor ideal antecipadamente; no entanto, para simplificar, inicializaremos ambos para 
.
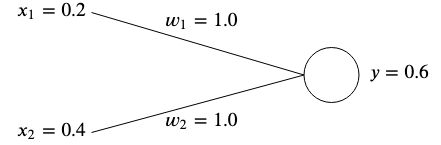
Se calcularmos a saída desta rede, obteremos
Se a saída não corresponde ao valor alvo esperado, então temos um erro.
Por exemplo, se quiséssemos obter um valor alvo de 
então teríamos uma diferença de
Uma maneira comum de medir o erro (também conhecido como função de custo) é usar o erro quadrático médio:
Se tivéssemos múltiplas associações de entradas e valores alvo, o erro se tornaria a soma média de cada associação.
Usamos o erro quadrático médio para medir a que distância os resultados estão da meta desejada. A quadratura remove os sinais negativos e dá mais peso às diferenças maiores entre o produto e a meta.
Para corrigir o erro, precisaríamos ajustar os pesos de forma que o resultado corresponda à nossa meta. No nosso exemplo, diminuindo de 
para 
faria o truque, já que
No entanto, para ajustar os pesos de nossas redes neurais para muitas entradas e valores alvo diferentes, precisamos de um algoritmo de aprendizagem que faça isso automaticamente para nós.
A ideia é usar o erro para entender como cada peso deve ser ajustado para que o erro seja minimizado, mas primeiro precisamos aprender sobre gradientes.
É essencialmente um vetor que aponta para a direção da subida mais íngreme de uma função. O gradiente é denotado com 
e é simplesmente a derivada parcial de cada variável de uma função expressa como um vetor.
Fica assim para uma função de duas variáveis:
Vamos injetar alguns números e calcular o gradiente com um exemplo simples. Digamos que temos uma função 
, então o gradiente seria
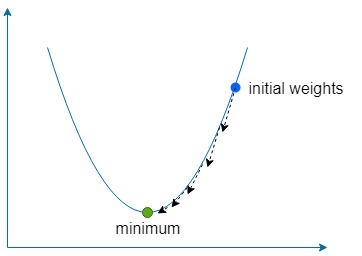
A parte de descida significa simplesmente usar o gradiente para encontrar a direção de subida mais íngreme de nossa função e, em seguida, ir um pouco na direção oposta muitas vezes para encontrar o mínimo global (ou às vezes local) da função.
Usamos uma constante chamada taxa de aprendizagem , denotada por 
para definir quão pequeno é o passo a ser dado nessa direção.
Se for muito grande, corremos o risco de ultrapassar o mínimo da função, mas se for muito baixo, a rede demorará mais para aprender e corremos o risco de ficar preso em um mínimo local superficial.
Para nossos dois pesos e precisamos encontrar o gradiente desses pesos em relação à função de erro 
Para ambos e , podemos encontrar o gradiente usando a regra da cadeia
De agora em diante denotaremos o 
como o 
termo para simplicidade.
Assim que tivermos o gradiente, podemos atualizar nossos pesos subtraindo o gradiente calculado vezes a taxa de aprendizado.
E repetimos esse processo até que o erro seja minimizado e próximo o suficiente de zero.
O exemplo incluído ensina o seguinte conjunto de dados para uma rede neural com duas entradas e uma saída usando gradiente descendente:
Uma vez aprendida, a rede deve produzir ~0 quando receber dois s e ~ quando dado um e um 
.
docker build -t simplest-network .
docker run --rm simplest-network
