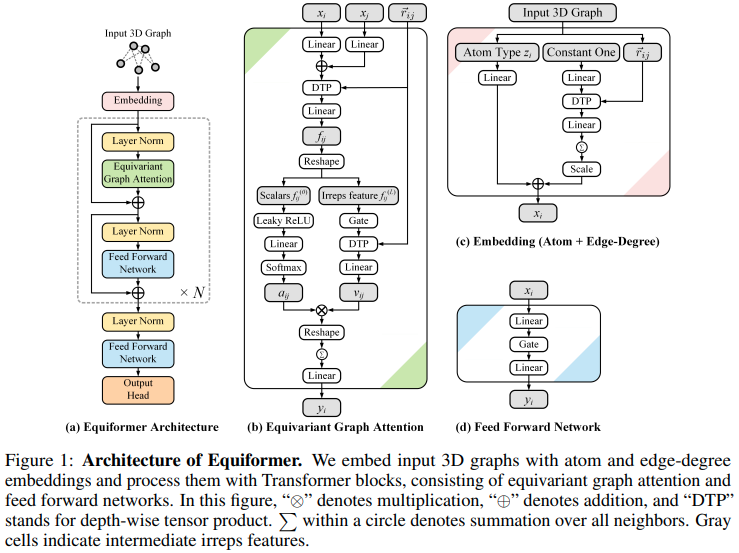
Download equiformer pytorch - download do código-fonte equiformer pytorch

Equiformador - Pytorch (wip)

Implementação do Equiformer, rede de atenção equivariante SE3/E3 que chega ao novo SOTA, e adotada para uso pelo EquiFold (Prescient Design) para enovelamento de proteínas

O design disso parece basear-se nos transformadores SE3, com a atenção do produto escalar substituída pela atenção MLP e passagem de mensagem não linear do GATv2. Ele também faz um produto tensor em profundidade para um pouco mais de eficiência. Se você acha que estou enganado, sinta-se à vontade para me enviar um e-mail.

Atualização: houve um novo desenvolvimento que torna o dimensionamento do número de graus para redes equivariantes SE3 dramaticamente melhor! Este artigo observou pela primeira vez que, ao alinhar as representações ao longo do eixo z (ou eixo y por alguma outra convenção), os harmônicos esféricos tornam-se esparsos. Isso remove a dimensão _mf da equação. Um artigo de acompanhamento de Passaro et al. observou que a matriz de Clebsch Gordan também se tornou esparsa, levando à remoção de m _i e l _f . Eles também estabeleceram a conexão de que o problema foi reduzido de SO(3) para SO(2) após alinhar as repetições em um eixo. Equiformer v2 (repositório oficial) aproveita isso em uma estrutura semelhante a um transformador para alcançar o novo SOTA.

Definitivamente colocarei mais trabalho/exploração nisso. Por enquanto, incorporei os truques dos dois primeiros artigos para Equiformer v1, exceto para conversão completa em SO(2).

Atualização 2: Parece haver um novo SOTA sem qualquer interação entre representantes de alto grau (em outras palavras, todo o produto tensorial / matemática clebsch gordan desaparece). GotenNet, que parece ser uma versão transformadora de HEGNN

Instalar

$ pip install equiformer-pytorch

Uso

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),               # dimensions per type, ascending, length must match number of degrees (num_degrees)
    dim_head = ( 4 , 4 , 4 ),          # dimension per attention head
    heads = ( 2 , 2 , 2 ),             # number of attention heads
    num_linear_attn_heads = 0 ,     # number of global linear attention heads, can see all the neighbors
    num_degrees = 3 ,               # number of degrees
    depth = 4 ,                     # depth of equivariant transformer
    attend_self = True ,            # attending to self or not
    reduce_dim_out = True ,         # whether to reduce out to dimension of 1, say for predicting new coordinates for type 1 features
    l2_dist_attention = False      # set to False to try out MLP attention
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask ) # (1, 128)

out . type0 # invariant type 0    - (1, 128)
out . type1 # equivariant type 1  - (1, 128, 3)

Este repositório também inclui uma maneira de dissociar o uso de memória da profundidade usando redes reversíveis. Em outras palavras, se você aumentar a profundidade, o custo de memória permanecerá constante no uso de um bloco transformador equiformador (atenção e feedforward).

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),
    dim_head = ( 4 , 4 , 4 ),
    heads = ( 2 , 2 , 2 ),
    num_degrees = 3 ,
    depth = 48 ,          # depth of 48 - just to show that it runs - in reality, seems to be quite unstable at higher depths, so architecture stil needs more work
    reversible = True ,   # just set this to True to use https://arxiv.org/abs/1707.04585
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask )

out . type0 . sum (). backward ()

Bordas

com bordas, ex. ligações atômicas

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

out = model ( atoms , coors , mask , edges = bonds )

out . type0 # (2, 32)
out . type1 # (2, 32, 3)

com matriz de adjacência

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    reduce_dim_out = True ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    num_adj_degrees_embed = 2 ,       # this will derive the second degree connections and embed it correctly
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat )

out . type0 # (1, 128)
out . type1 # (1, 128, 3)

Apreciação

StabilityAI pelo patrocínio generoso, assim como meus outros patrocinadores por aí

Teste

Testes de equivariância etc.

$ python setup.py test

Exemplo

Primeiro instale sidechainnet

$ pip install sidechainnet

Em seguida, execute a tarefa de remoção de ruído do backbone da proteína

$ python denoise.py

Pendência

Citações

 @article { Liao2022EquiformerEG ,
    title   = { Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs } ,
    author  = { Yi Liao and Tess E. Smidt } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.11990 }
}

 @article { Lee2022.10.07.511322 ,
    author  = { Lee, Jae Hyeon and Yadollahpour, Payman and Watkins, Andrew and Frey, Nathan C. and Leaver-Fay, Andrew and Ra, Stephen and Cho, Kyunghyun and Gligorijevic, Vladimir and Regev, Aviv and Bonneau, Richard } ,
    title   = { EquiFold: Protein Structure Prediction with a Novel Coarse-Grained Structure Representation } ,
    elocation-id = { 2022.10.07.511322 } ,
    year    = { 2022 } ,
    doi     = { 10.1101/2022.10.07.511322 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322 } ,
    eprint  = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Shazeer2019FastTD ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam M. Shazeer } ,
    journal = { ArXiv } ,
    year    = { 2019 } ,
    volume  = { abs/1911.02150 }
}

 @misc { ding2021cogview ,
    title   = { CogView: Mastering Text-to-Image Generation via Transformers } ,
    author  = { Ming Ding and Zhuoyi Yang and Wenyi Hong and Wendi Zheng and Chang Zhou and Da Yin and Junyang Lin and Xu Zou and Zhou Shao and Hongxia Yang and Jie Tang } ,
    year    = { 2021 } ,
    eprint  = { 2105.13290 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @inproceedings { Kim2020TheLC ,
    title   = { The Lipschitz Constant of Self-Attention } ,
    author  = { Hyunjik Kim and George Papamakarios and Andriy Mnih } ,
    booktitle = { International Conference on Machine Learning } ,
    year    = { 2020 }
}

 @article { Zitnick2022SphericalCF ,
    title   = { Spherical Channels for Modeling Atomic Interactions } ,
    author  = { C. Lawrence Zitnick and Abhishek Das and Adeesh Kolluru and Janice Lan and Muhammed Shuaibi and Anuroop Sriram and Zachary W. Ulissi and Brandon C. Wood } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.14331 }
}

 @article { Passaro2023ReducingSC ,
  title     = { Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs } ,
  author    = { Saro Passaro and C. Lawrence Zitnick } ,
  journal   = { ArXiv } ,
  year      = { 2023 } ,
  volume    = { abs/2302.03655 }
}

 @inproceedings { Gomez2017TheRR ,
    title   = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author  = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger Baker Grosse } ,
    booktitle = { NIPS } ,
    year    = { 2017 }
}

 @article { Bondarenko2023QuantizableTR ,
    title   = { Quantizable Transformers: Removing Outliers by Helping Attention Heads Do Nothing } ,
    author  = { Yelysei Bondarenko and Markus Nagel and Tijmen Blankevoort } ,
    journal = { ArXiv } ,
    year    = { 2023 } ,
    volume  = { abs/2306.12929 } ,
    url     = { https://api.semanticscholar.org/CorpusID:259224568 }
}

 @inproceedings { Arora2023ZoologyMA ,
  title   = { Zoology: Measuring and Improving Recall in Efficient Language Models } ,
  author  = { Simran Arora and Sabri Eyuboglu and Aman Timalsina and Isys Johnson and Michael Poli and James Zou and Atri Rudra and Christopher R'e } ,
  year    = { 2023 } ,
  url     = { https://api.semanticscholar.org/CorpusID:266149332 }
}