7 funções JavaScript simples que lhe darão uma ideia de como as máquinas podem realmente “aprender”.
Em outros idiomas: Русский, Português
Você também pode estar interessado em? Experimentos interativos de aprendizado de máquina
NanoNeuron é uma versão simplificada do conceito Neuron da Neural Networks. NanoNeuron é treinado para converter valores de temperatura de Celsius para Fahrenheit.
O exemplo de código NanoNeuron.js contém 7 funções JavaScript simples (que abordam previsão de modelo, cálculo de custos, propagação direta/regressiva e treinamento) que lhe darão uma ideia de como as máquinas podem realmente "aprender". Sem bibliotecas de terceiros, sem conjuntos de dados externos ou dependências, apenas funções JavaScript puras e simples.
☝?Essas funções NÃO são, de forma alguma, um guia completo para aprendizado de máquina. Muitos conceitos de aprendizado de máquina são ignorados e simplificados demais! Essa simplificação é feita propositalmente para dar ao leitor uma compreensão e uma sensação realmente básicas de como as máquinas podem aprender e, em última análise, para tornar possível ao leitor reconhecer que não se trata de "aprendizado de máquina MAGIC", mas sim de "aprendizado de máquina MATEMÁTICA"?.
Você provavelmente já ouviu falar sobre Neurônios no contexto de Redes Neurais. NanoNeuron é exatamente isso, mas mais simples e vamos implementá-lo do zero. Por razões de simplicidade, nem sequer vamos construir uma rede baseada em NanoNeurons. Teremos tudo funcionando por conta própria, fazendo algumas previsões mágicas para nós. Ou seja, ensinaremos este NanoNeuron singular a converter (prever) a temperatura de Celsius para Fahrenheit.
A propósito, a fórmula para converter Celsius em Fahrenheit é esta:
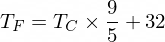
Mas por enquanto nosso NanoNeuron não sabe disso...
Vamos implementar nossa função de modelo NanoNeuron. Ele implementa dependência linear básica entre x e y , que se parece com y = w * x + b . Simplesmente dizendo que nosso NanoNeuron é uma “criança” em uma “escola” que está sendo ensinada a desenhar linhas retas em coordenadas XY .
As variáveis w , b são parâmetros do modelo. NanoNeuron conhece apenas esses dois parâmetros da função linear. Esses parâmetros são algo que o NanoNeuron vai “aprender” durante o processo de treinamento.
A única coisa que o NanoNeuron pode fazer é imitar a dependência linear. Em seu método predict() ele aceita alguma entrada x e prevê a saída y . Não há mágica aqui.
function NanoNeuron ( w , b ) {
this . w = w ;
this . b = b ;
this . predict = ( x ) => {
return x * this . w + this . b ;
}
}(...espere... regressão linear, é você?) ?
O valor da temperatura em Celsius pode ser convertido para Fahrenheit usando a seguinte fórmula: f = 1.8 * c + 32 , onde c é a temperatura em Celsius e f é a temperatura calculada em Fahrenheit.
function celsiusToFahrenheit ( c ) {
const w = 1.8 ;
const b = 32 ;
const f = c * w + b ;
return f ;
} ; Em última análise, queremos ensinar nosso NanoNeuron a imitar esta função (para aprender que w = 1.8 b = 32 ) sem conhecer esses parâmetros antecipadamente.
Esta é a aparência da função de conversão de Celsius para Fahrenheit:
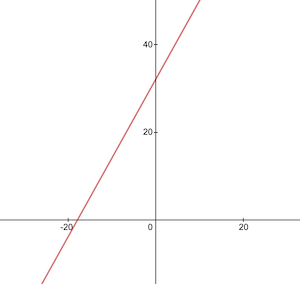
Antes do treinamento, precisamos gerar conjuntos de dados de treinamento e teste com base na função celsiusToFahrenheit() . Os conjuntos de dados consistem em pares de valores de entrada e valores de saída rotulados corretamente.
Na vida real, na maioria dos casos, estes dados seriam recolhidos em vez de gerados. Por exemplo, podemos ter um conjunto de imagens de números desenhados à mão e o conjunto de números correspondente que explica qual número está escrito em cada imagem.
Usaremos dados de exemplo de TRAINING para treinar nosso NanoNeuron. Antes que nosso NanoNeuron cresça e seja capaz de tomar decisões por conta própria, precisamos ensiná-lo o que é certo e o que é errado usando exemplos de treinamento.
Usaremos exemplos de TESTE para avaliar o desempenho do nosso NanoNeuron nos dados que não viu durante o treinamento. Este é o ponto onde pudemos ver que o nosso “filho” cresceu e pode tomar decisões por conta própria.
function generateDataSets ( ) {
// xTrain -> [0, 1, 2, ...],
// yTrain -> [32, 33.8, 35.6, ...]
const xTrain = [ ] ;
const yTrain = [ ] ;
for ( let x = 0 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTrain . push ( x ) ;
yTrain . push ( y ) ;
}
// xTest -> [0.5, 1.5, 2.5, ...]
// yTest -> [32.9, 34.7, 36.5, ...]
const xTest = [ ] ;
const yTest = [ ] ;
// By starting from 0.5 and using the same step of 1 as we have used for training set
// we make sure that test set has different data comparing to training set.
for ( let x = 0.5 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTest . push ( x ) ;
yTest . push ( y ) ;
}
return [ xTrain , yTrain , xTest , yTest ] ;
} Precisamos de alguma métrica que nos mostre o quão próxima a previsão do nosso modelo está dos valores corretos. O cálculo do custo (o erro) entre o valor correto de saída de y e prediction , que nosso NanoNeuron criou, será feito usando a seguinte fórmula:
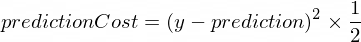
Esta é uma diferença simples entre dois valores. Quanto mais próximos os valores estiverem entre si, menor será a diferença. Estamos usando uma potência de 2 aqui apenas para nos livrar dos números negativos, de modo que (1 - 2) ^ 2 seja igual a (2 - 1) ^ 2 . A divisão por 2 está acontecendo apenas para simplificar ainda mais a fórmula de propagação para trás (veja abaixo).
A função de custo neste caso será tão simples como:
function predictionCost ( y , prediction ) {
return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
} Fazer propagação direta significa fazer uma previsão para todos os exemplos de treinamento dos conjuntos de dados xTrain e yTrain e calcular o custo médio dessas previsões ao longo do caminho.
Nós apenas deixamos nosso NanoNeuron dizer sua opinião, neste momento, apenas permitindo que ele adivinhe como converter a temperatura. Pode estar estupidamente errado aqui. O custo médio nos mostrará o quão errado nosso modelo está agora. Este valor de custo é muito importante desde a alteração dos parâmetros w e b do NanoNeuron, e fazendo a propagação direta novamente; poderemos avaliar se nosso NanoNeuron ficou mais inteligente ou não após a mudança desses parâmetros.
O custo médio será calculado usando a seguinte fórmula:
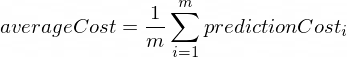
Onde m é um número de exemplos de treinamento (no nosso caso: 100 ).
Aqui está como podemos implementá-lo em código:
function forwardPropagation ( model , xTrain , yTrain ) {
const m = xTrain . length ;
const predictions = [ ] ;
let cost = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
cost += predictionCost ( yTrain [ i ] , prediction ) ;
predictions . push ( prediction ) ;
}
// We are interested in average cost.
cost /= m ;
return [ predictions , cost ] ;
}Quando sabemos o quão certas ou erradas estão as previsões do nosso NanoNeuron (com base no custo médio neste momento), o que devemos fazer para tornar as previsões mais precisas?
A propagação para trás nos dá a resposta a esta pergunta. A propagação retroativa é o processo de avaliar o custo da previsão e ajustar os parâmetros w e b do NanoNeuron para que as próximas e futuras previsões sejam mais precisas.
Este é o lugar onde o aprendizado de máquina parece mágica ?♂️. O conceito chave aqui é a derivada que mostra que passo tomar para se aproximar do mínimo da função de custo.
Lembre-se de que encontrar o mínimo de uma função de custo é o objetivo final do processo de treinamento. Se encontrarmos tais valores para w e b de modo que nossa função de custo médio seja pequena, isso significaria que o modelo NanoNeuron faz previsões realmente boas e precisas.
Os derivativos são um tópico grande e separado que não abordaremos neste artigo. MathIsFun é um bom recurso para obter uma compreensão básica dele.
Uma coisa sobre as derivadas que o ajudará a entender como funciona a propagação para trás é que a derivada, pelo seu significado, é uma linha tangente à curva da função que aponta na direção do mínimo da função.
Fonte da imagem: MathIsFun
Por exemplo, no gráfico acima, você pode ver que se estivermos no ponto (x=2, y=4) , então a inclinação nos diz para ir left e down para chegar ao mínimo da função. Observe também que quanto maior a inclinação, mais rápido devemos nos mover para o mínimo.
As derivadas de nossa função averageCost para os parâmetros w e b são assim:
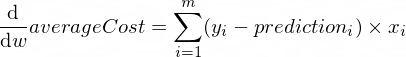
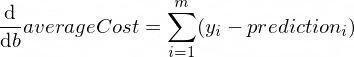
Onde m é um número de exemplos de treinamento (no nosso caso: 100 ).
Você pode ler mais sobre regras de derivadas e como obter derivadas de funções complexas aqui.
function backwardPropagation ( predictions , xTrain , yTrain ) {
const m = xTrain . length ;
// At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
// Therefore we're setting up the changing steps for each parameters to 0.
let dW = 0 ;
let dB = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
dB += yTrain [ i ] - predictions [ i ] ;
}
// We're interested in average deltas for each params.
dW /= m ;
dB /= m ;
return [ dW , dB ] ;
} Agora sabemos como avaliar a correção do nosso modelo para todos os exemplos de conjuntos de treinamento ( propagação direta ). Também sabemos fazer pequenos ajustes nos parâmetros w e b do nosso modelo NanoNeuron ( propagação para trás ). Mas o problema é que se executarmos a propagação para frente e depois para trás apenas uma vez, não será suficiente para nosso modelo aprender quaisquer leis/tendências a partir dos dados de treinamento. Você pode compará-lo com frequentar um dia de escola primária para a criança. Ele/ela deveria ir à escola não uma vez, mas dia após dia e ano após ano para aprender alguma coisa.
Portanto, precisamos repetir a propagação direta e reversa do nosso modelo muitas vezes. Isso é exatamente o que a função trainModel() faz. É como um “professor” para o nosso modelo NanoNeuron:
epochs ) com nosso modelo NanoNeuron um pouco estúpido e tentará treiná-lo/ensiná-lo,xTrain e yTrain ) para treinamento,alpha Algumas palavras sobre a taxa de aprendizagem alpha . Este é apenas um multiplicador para os valores de dW e dB que calculamos durante a propagação retroativa. Portanto, a derivada nos apontou a direção que precisamos seguir para encontrar o mínimo da função de custo (sinal dW e dB ) e também nos mostrou o quão rápido precisamos ir nessa direção (valores absolutos de dW e dB ). Agora precisamos multiplicar esses tamanhos de passo para alpha apenas para ajustar nosso movimento ao mínimo, mais rápido ou mais lento. Às vezes, se usarmos valores grandes para alpha , podemos simplesmente pular o mínimo e nunca encontrá-lo.
A analogia com o professor seria que quanto mais ele/ela pressiona o nosso “nano-criança”, mais rápido o nosso “nano-criança” aprenderá, mas se o professor pressionar demais, a “criança” terá um colapso nervoso e vencerá. não ser capaz de aprender nada?
Aqui está como vamos atualizar os parâmetros w e b do nosso modelo:
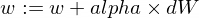
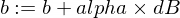
E aqui está nossa função de treinador:
function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
// The is the history array of how NanoNeuron learns.
const costHistory = [ ] ;
// Let's start counting epochs.
for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
// Forward propagation.
const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
costHistory . push ( cost ) ;
// Backward propagation.
const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
// Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
nanoNeuron . w += alpha * dW ;
nanoNeuron . b += alpha * dB ;
}
return costHistory ;
}Agora vamos usar as funções que criamos acima.
Vamos criar nossa instância do modelo NanoNeuron. Neste momento o NanoNeuron não sabe quais valores devem ser definidos para os parâmetros w e b . Então, vamos configurar w e b aleatoriamente.
const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;Gere conjuntos de dados de treinamento e teste.
const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ; Vamos treinar o modelo com pequenos passos incrementais ( 0.0005 ) por 70000 épocas. Você pode brincar com esses parâmetros, eles estão sendo definidos empiricamente.
const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;Vamos verificar como a função custo mudou durante o treinamento. Esperamos que o custo após o treinamento seja muito menor do que antes. Isso significaria que o NanoNeuron ficou mais inteligente. O oposto também é possível.
console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024 É assim que o custo do treinamento muda ao longo das épocas. Nos eixos x está o número da época x1000.
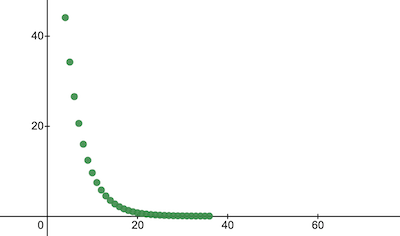
Vamos dar uma olhada nos parâmetros do NanoNeuron para ver o que ele aprendeu. Esperamos que os parâmetros do NanoNeuron w e b sejam semelhantes aos que temos na função celsiusToFahrenheit() ( w = 1.8 e b = 32 ), já que nosso NanoNeuron tentou imitá-lo.
console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}Avalie a precisão do modelo para o conjunto de dados de teste para ver quão bem nosso NanoNeuron lida com novas previsões de dados desconhecidos. Espera-se que o custo das previsões em conjuntos de testes seja próximo do custo de treinamento. Isso significaria que nosso NanoNeuron funciona bem com dados conhecidos e desconhecidos.
[ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023Agora, como vemos que nosso “garoto” NanoNeuron teve um bom desempenho na “escola” durante o treinamento e que consegue converter temperaturas Celsius em Fahrenheit corretamente, mesmo para os dados que não viu, podemos chamá-lo de “inteligente” e faça algumas perguntas a ele. Este foi o objetivo final de todo o processo de treinamento.
const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158Tão perto! Como todos nós, humanos, nosso NanoNeuron é bom, mas não é o ideal :)
Feliz aprendizado para você!
Você pode clonar o repositório e executá-lo localmente:
git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuronnode ./NanoNeuron.jsOs seguintes conceitos de aprendizado de máquina foram ignorados e simplificados para simplificar a explicação.
Divisão de conjunto de dados de treinamento/teste
Normalmente você tem um grande conjunto de dados. Dependendo do número de exemplos nesse conjunto, você pode querer dividi-lo na proporção de 70/30 para conjuntos de treinamento/teste. Os dados do conjunto devem ser embaralhados aleatoriamente antes da divisão. Se o número de exemplos for grande (ou seja, milhões), então a divisão poderá ocorrer em proporções mais próximas de 90/10 ou 95/5 para conjuntos de dados de treinamento/teste.
A rede traz o poder
Normalmente você não notará o uso de apenas um neurônio independente. O poder está na rede desses neurônios. A rede pode aprender recursos muito mais complexos. O NanoNeuron sozinho parece mais uma regressão linear simples do que uma rede neural.
Normalização de entrada
Antes do treinamento, seria melhor normalizar os valores de entrada.
Implementação vetorizada
Para redes, os cálculos vetorizados (matrizes) funcionam muito mais rápido do que for loops. Normalmente a propagação para frente/para trás funciona muito mais rápido se for implementada em formato vetorizado e calculada usando, por exemplo, a biblioteca Numpy Python.
Mínimo da função de custo
A função de custo que estávamos usando neste exemplo é simplificada demais. Deve ter componentes logarítmicos. Alterar a função de custo também alterará suas derivadas, de modo que a etapa de retropropagação também usaria fórmulas diferentes.
Função de ativação
Normalmente a saída de um neurônio deve passar por uma função de ativação como Sigmoid ou ReLU ou outras.