Uma implementação do algoritmo Minimax AI no jogo Tic-Tac-Toe (ou Nada e Cruzes). Experimente: Jogo da Velha - Minimax
Para resolver jogos usando IA, apresentaremos o conceito de árvore de jogo seguido pelo algoritmo minimax. Os diferentes estados do jogo são representados por nós na árvore do jogo, muito semelhantes aos problemas de planejamento acima. A ideia é apenas um pouco diferente. Na árvore do jogo, os nós são organizados em níveis que correspondem aos turnos de cada jogador no jogo, de modo que o nó “raiz” da árvore (geralmente representado no topo do diagrama) seja a posição inicial do jogo. No jogo da velha, esta seria a grade vazia, sem nenhum X ou Os jogado ainda. Abaixo da raiz, no segundo nível, estão os estados possíveis que podem resultar dos movimentos do primeiro jogador, seja ele X ou O. Chamamos esses nós de “filhos” do nó raiz.
Cada nó no segundo nível teria ainda como nós filhos os estados que podem ser alcançados a partir dele pelos movimentos do jogador adversário. Isto continua, nível por nível, até chegar aos estados onde o jogo termina. No jogo da velha, isso significa que ou um dos jogadores consegue uma linha de três e vence, ou o tabuleiro fica cheio e o jogo termina empatado.
Minimax é uma inteligência artificial aplicada em jogos para dois jogadores, como jogo da velha, damas, xadrez e go. Estes jogos são conhecidos como jogos de soma zero, porque numa representação matemática: um jogador ganha (+1) e outro jogador perde (-1) ou ambos não ganham (0).
O algoritmo busca, recursivamente, a melhor jogada que leve o jogador Max a vencer ou não perder (empate). Ele considera o estado atual do jogo e os movimentos disponíveis nesse estado e, em seguida, para cada movimento válido, ele joga (alternando min e max ) até encontrar um estado terminal (vitória, empate ou derrota).
O algoritmo foi estudado pelo livro Algorithms in a Nutshell (George Heineman; Gary Pollice; Stanley Selkow, 2009). Pseudocódigo (adaptado):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
Agora veremos cada parte deste pseudocódigo com implementação em Python. A implementação do Python está disponível neste repositório. Em primeiro lugar, considere isso:
tabuleiro = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
MÁX = +1
MÍN = -1
O MAX pode ser X ou O e o MIN pode ser O ou X, tanto faz. O tabuleiro é 3x3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]Ambos os jogadores começam com a sua pior pontuação. Se o jogador for MAX, sua pontuação será -infinito. Caso contrário, se o jogador for MIN, sua pontuação será + infinito. Nota: infinito é um alias para inf (do módulo matemático, em Python).
A melhor jogada no tabuleiro é [-1, -1] (linha e coluna) para todos.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreSe a profundidade for igual a zero, então o tabuleiro não terá novas células vazias para jogar. Ou, se um jogador vencer, o jogo terminou em MAX ou MIN. Portanto, a pontuação desse estado será retornada.
Agora veremos a parte principal deste código que contém recursão.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yPara cada movimento válido (células vazias):
O movimento (+1 ou -1) no tabuleiro é desfeito e a linha e coluna são coletadas.
O próximo passo é comparar a pontuação com a melhor.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scorePara o jogador MAX, uma pontuação maior será recebida. Para um jogador MIN, será recebida uma pontuação mais baixa. E no final, a melhor jogada é devolvida. Algoritmo final:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best Abaixo, o melhor movimento está no meio porque o valor máximo está no segundo nó à esquerda.
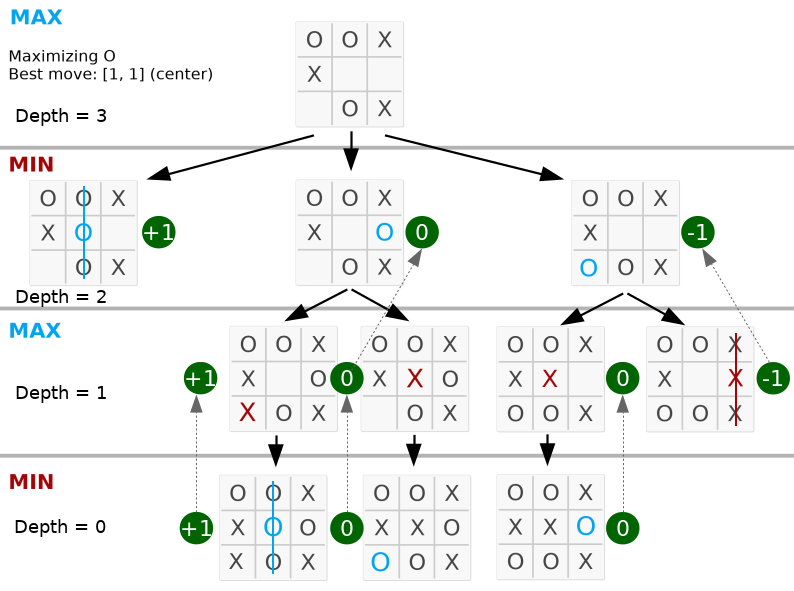
Observe que a profundidade é igual aos movimentos válidos no tabuleiro. O código completo está disponível em py_version/ .
Árvore de jogo simplificada:
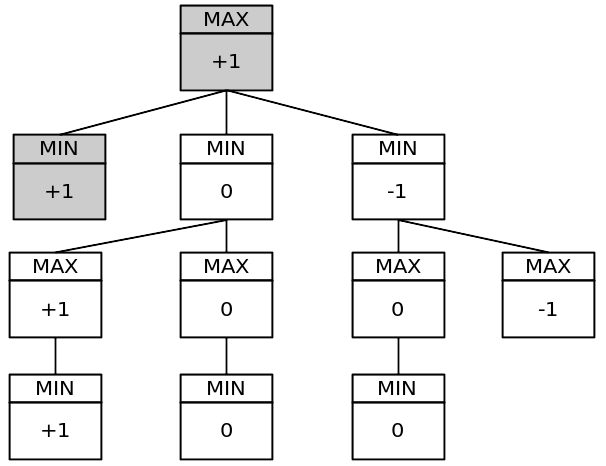
Essa árvore tem 11 nós. A árvore completa do jogo possui 549.946 nós! Você pode testá-lo colocando uma variável global estática em seu programa e incrementando-a para cada chamada de função minimax por turno.
Em um jogo mais complexo, como o xadrez, é difícil pesquisar toda a árvore do jogo. Porém, Alpha-beta Pruning é um método de otimização do algoritmo minimax que nos permite desconsiderar alguns ramos da árvore de busca, pois corta nós irrelevantes (subárvores) na busca. Para obter mais informações, consulte: