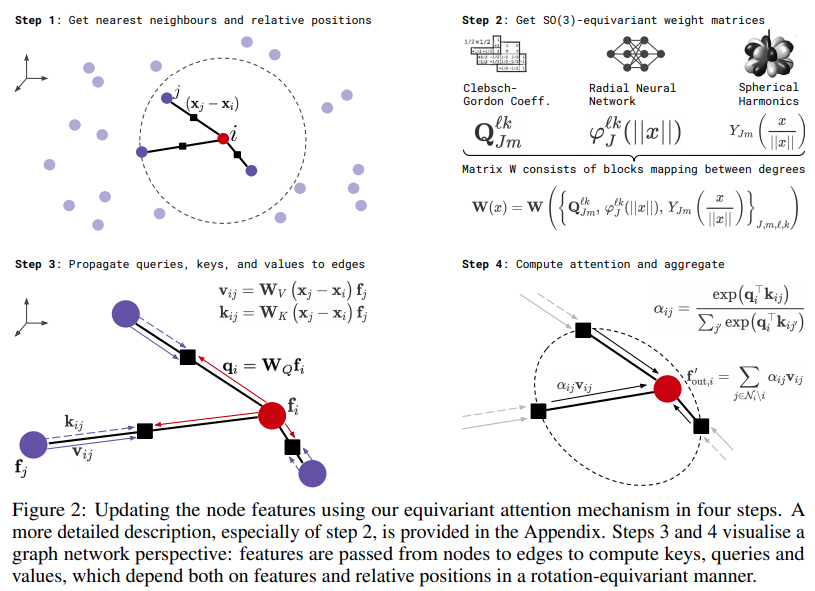
Implementação de Transformadores SE3 para Autoatenção Equivariante, em Pytorch. Pode ser necessário para replicar resultados do Alphafold2 e outras aplicações de descoberta de medicamentos.
Exemplo de equivariância
Se você estava usando alguma versão do SE3 Transformers anterior à versão 0.6.0, atualize. Um grande bug foi descoberto por @MattMcPartlon, se você não estivesse usando as configurações de vizinhos esparsos de adjacência e confiando na funcionalidade de vizinhos mais próximos
Atualização: é recomendado que você use o Equiformer
$ pip install se3-transformer-pytorch import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 512 ,
heads = 8 ,
depth = 6 ,
dim_head = 64 ,
num_degrees = 4 ,
valid_radius = 10
)
feats = torch . randn ( 1 , 1024 , 512 )
coors = torch . randn ( 1 , 1024 , 3 )
mask = torch . ones ( 1 , 1024 ). bool ()
out = model ( feats , coors , mask ) # (1, 1024, 512)Potencial exemplo de uso no Alphafold2, conforme descrito aqui
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 2 ,
input_degrees = 1 ,
num_degrees = 2 ,
output_degrees = 2 ,
reduce_dim_out = True ,
differentiable_coors = True
)
atom_feats = torch . randn ( 2 , 32 , 64 )
coors = torch . randn ( 2 , 32 , 3 )
mask = torch . ones ( 2 , 32 ). bool ()
refined_coors = coors + model ( atom_feats , coors , mask , return_type = 1 ) # (2, 32, 3)Você também pode deixar a classe base do transformador cuidar de incorporar os recursos do tipo 0 que estão sendo passados.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
num_tokens = 28 , # 28 unique atoms
dim = 64 ,
depth = 2 ,
input_degrees = 1 ,
num_degrees = 2 ,
output_degrees = 2 ,
reduce_dim_out = True
)
atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask = torch . ones ( 2 , 32 ). bool ()
refined_coors = coors + model ( atoms , coors , mask , return_type = 1 ) # (2, 32, 3)Se você acha que a rede poderia se beneficiar ainda mais com a codificação posicional, você pode caracterizar suas posições no espaço e transmiti-las da seguinte maneira.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 2 ,
input_degrees = 2 ,
num_degrees = 2 ,
output_degrees = 2 ,
reduce_dim_out = True # reduce out the final dimension
)
atom_feats = torch . randn ( 2 , 32 , 64 , 1 ) # b x n x d x type0
coors_feats = torch . randn ( 2 , 32 , 64 , 3 ) # b x n x d x type1
# atom features are type 0, predicted coordinates are type 1
features = { '0' : atom_feats , '1' : coors_feats }
coors = torch . randn ( 2 , 32 , 3 )
mask = torch . ones ( 2 , 32 ). bool ()
refined_coors = coors + model ( features , coors , mask , return_type = 1 ) # (2, 32, 3) - equivariant to input type 1 features and coordinates Para oferecer informações de borda aos transformadores SE3 (digamos, tipos de ligação entre átomos), basta passar mais dois argumentos de palavras-chave na inicialização.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
num_tokens = 28 ,
dim = 64 ,
num_edge_tokens = 4 , # number of edge type, say 4 bond types
edge_dim = 16 , # dimension of edge embedding
depth = 2 ,
input_degrees = 1 ,
num_degrees = 3 ,
output_degrees = 1 ,
reduce_dim_out = True
)
atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask = torch . ones ( 2 , 32 ). bool ()
pred = model ( atoms , coors , mask , edges = bonds , return_type = 0 ) # (2, 32, 1) Se desejar passar valores contínuos para suas arestas, você pode optar por não definir num_edge_tokens , codificar seus tipos de títulos discretos e, em seguida, concatá-los com os recursos de Fourier desses valores contínuos
import torch
from se3_transformer_pytorch import SE3Transformer
from se3_transformer_pytorch . utils import fourier_encode
model = SE3Transformer (
dim = 64 ,
depth = 1 ,
attend_self = True ,
num_degrees = 2 ,
output_degrees = 2 ,
edge_dim = 34 # edge dimension must match the final dimension of the edges being passed in
)
feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask = torch . ones ( 1 , 32 ). bool ()
pairwise_continuous_values = torch . randint ( 0 , 4 , ( 1 , 32 , 32 , 2 )) # say there are 2
edges = fourier_encode (
pairwise_continuous_values ,
num_encodings = 8 ,
include_self = True
) # (1, 32, 32, 34) - {2 * (2 * 8 + 1)}
out = model ( feats , coors , mask , edges = edges , return_type = 1 ) Se você conhece a conectividade dos seus pontos (digamos que está trabalhando com moléculas), você pode passar uma matriz de adjacência, na forma de uma máscara booleana (onde True indica conectividade).
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 32 ,
heads = 8 ,
depth = 1 ,
dim_head = 64 ,
num_degrees = 2 ,
valid_radius = 10 ,
attend_sparse_neighbors = True , # this must be set to true, in which case it will assert that you pass in the adjacency matrix
num_neighbors = 0 , # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
max_sparse_neighbors = 8 # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)
feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask = torch . ones ( 1 , 128 ). bool ()
# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)
i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))
out = model ( feats , coors , mask , adj_mat = adj_mat ) # (1, 128, 512) Você também pode fazer com que a rede derive automaticamente para você os vizinhos de enésimo grau com uma palavra-chave extra num_adj_degrees . Se você quiser que o sistema diferencie o grau dos vizinhos como informações de borda, passe ainda um adj_dim diferente de zero.
import torch
from se3_transformer_pytorch . se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 1 ,
attend_self = True ,
num_degrees = 2 ,
output_degrees = 2 ,
num_neighbors = 0 ,
attend_sparse_neighbors = True ,
num_adj_degrees = 2 , # automatically derive 2nd degree neighbors
adj_dim = 4 # embed 1st and 2nd degree neighbors (as well as null neighbors) with edge embeddings of this dimension
)
feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask = torch . ones ( 1 , 32 ). bool ()
# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)
i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))
out = model ( feats , coors , mask , adj_mat = adj_mat , return_type = 1 ) Para ter um controle preciso sobre a dimensionalidade de cada tipo, você pode usar as palavras-chave hidden_fiber_dict e out_fiber_dict para passar um dicionário com o grau dos valores de dimensão como chave/valores.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
num_tokens = 28 ,
dim = 64 ,
num_edge_tokens = 4 ,
edge_dim = 16 ,
depth = 2 ,
input_degrees = 1 ,
num_degrees = 3 ,
output_degrees = 1 ,
hidden_fiber_dict = { 0 : 16 , 1 : 8 , 2 : 4 },
out_fiber_dict = { 0 : 16 , 1 : 1 },
reduce_dim_out = False
)
atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask = torch . ones ( 2 , 32 ). bool ()
pred = model ( atoms , coors , mask , edges = bonds )
pred [ '0' ] # (2, 32, 16)
pred [ '1' ] # (2, 32, 1, 3) Você pode controlar ainda mais quais nós podem ser considerados passando uma máscara de vizinho. Todos os valores False serão mascarados fora de consideração.
import torch
from se3_transformer_pytorch . se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 16 ,
dim_head = 16 ,
attend_self = True ,
num_degrees = 4 ,
output_degrees = 2 ,
num_edge_tokens = 4 ,
num_neighbors = 8 , # make sure you set this value as the maximum number of neighbors set by your neighbor_mask, or it will throw a warning
edge_dim = 2 ,
depth = 3
)
feats = torch . randn ( 1 , 32 , 16 )
coors = torch . randn ( 1 , 32 , 3 )
mask = torch . ones ( 1 , 32 ). bool ()
bonds = torch . randint ( 0 , 4 , ( 1 , 32 , 32 ))
neighbor_mask = torch . ones ( 1 , 32 , 32 ). bool () # set the nodes you wish to be masked out as False
out = model (
feats ,
coors ,
mask ,
edges = bonds ,
neighbor_mask = neighbor_mask ,
return_type = 1
)Este recurso permite que você passe vetores que podem ser visualizados como nós globais que são vistos por todos os outros nós. A ideia seria agrupar seu gráfico em alguns vetores de recursos, que serão projetados em chaves/valores em todas as camadas de atenção da rede. Todos os nós terão acesso total às informações globais do nó, independentemente dos vizinhos mais próximos ou do cálculo de adjacência.
import torch
from torch import nn
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 1 ,
num_degrees = 2 ,
num_neighbors = 4 ,
valid_radius = 10 ,
global_feats_dim = 32 # this must be set to the dimension of the global features, in this example, 32
)
feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask = torch . ones ( 1 , 32 ). bool ()
# naively derive global features
# by pooling features and projecting
global_feats = nn . Linear ( 64 , 32 )( feats . mean ( dim = 1 , keepdim = True )) # (1, 1, 32)
out = model ( feats , coors , mask , return_type = 0 , global_feats = global_feats )Pendência:
Você pode usar transformadores SE3 de forma autorregressiva com apenas um sinalizador extra
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 512 ,
heads = 8 ,
depth = 6 ,
dim_head = 64 ,
num_degrees = 4 ,
valid_radius = 10 ,
causal = True # set this to True
)
feats = torch . randn ( 1 , 1024 , 512 )
coors = torch . randn ( 1 , 1024 , 3 )
mask = torch . ones ( 1 , 1024 ). bool ()
out = model ( feats , coors , mask ) # (1, 1024, 512) Descobri que o uso de chaves projetadas linearmente (em vez da convolução em pares) parece funcionar bem em uma tarefa de eliminação de ruído de brinquedo. Isso leva a uma economia de memória de 25%. Você pode experimentar este recurso definindo linear_proj_keys = True
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 1 ,
num_degrees = 4 ,
num_neighbors = 8 ,
valid_radius = 10 ,
splits = 4 ,
linear_proj_keys = True # set this to True
). cuda ()
feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask = torch . ones ( 1 , 32 ). bool (). cuda ()
out = model ( feats , coors , mask , return_type = 0 )Existe uma técnica relativamente desconhecida para transformadores, onde é possível compartilhar um cabeçalho de chave/valor em todos os cabeçalhos das consultas. Na minha experiência em PNL, isso geralmente leva a um desempenho pior, mas se você realmente precisar trocar a memória por mais profundidade ou maior número de graus, esta pode ser uma boa opção.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 8 ,
num_degrees = 4 ,
num_neighbors = 8 ,
valid_radius = 10 ,
splits = 4 ,
one_headed_key_values = True # one head of key / values shared across all heads of the queries
). cuda ()
feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask = torch . ones ( 1 , 32 ). bool (). cuda ()
out = model ( feats , coors , mask , return_type = 0 )Você também pode vincular as chaves/valores (fazê-los iguais), para economizar metade da memória
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 64 ,
depth = 8 ,
num_degrees = 4 ,
num_neighbors = 8 ,
valid_radius = 10 ,
splits = 4 ,
tie_key_values = True # set this to True
). cuda ()
feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask = torch . ones ( 1 , 32 ). bool (). cuda ()
out = model ( feats , coors , mask , return_type = 0 ) Esta é uma versão experimental do EGNN que funciona para tipos superiores e com maior dimensionalidade do que apenas 1 (para as coordenadas). O nome da classe ainda é SE3Transformer , pois reutiliza alguma lógica pré-existente, então ignore isso por enquanto até que eu limpe tudo mais tarde.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 32 ,
num_neighbors = 8 ,
num_edge_tokens = 4 ,
edge_dim = 4 ,
num_degrees = 4 , # number of higher order types - will use basis on a TCN to project to these dimensions
use_egnn = True , # set this to true to use EGNN instead of equivariant attention layers
egnn_hidden_dim = 64 , # egnn hidden dimension
depth = 4 , # depth of EGNN
reduce_dim_out = True # will project the dimension of the higher types to 1
). cuda ()
feats = torch . randn ( 2 , 32 , 32 ). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 )). cuda ()
mask = torch . ones ( 2 , 32 ). bool (). cuda ()
refinement = model ( feats , coors , mask , edges = bonds , return_type = 1 ) # (2, 32, 3)
coors = coors + refinement # update coors with refinement Se você quiser especificar dimensões individuais para cada um dos tipos superiores, basta passar hidden_fiber_dict onde o dicionário está no formato {<degree>:<dim>} em vez de num_degrees
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
dim = 32 ,
num_neighbors = 8 ,
hidden_fiber_dict = { 0 : 32 , 1 : 16 , 2 : 8 , 3 : 4 },
use_egnn = True ,
depth = 4 ,
egnn_hidden_dim = 64 ,
egnn_weights_clamp_value = 2 ,
reduce_dim_out = True
). cuda ()
feats = torch . randn ( 2 , 32 , 32 ). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
mask = torch . ones ( 2 , 32 ). bool (). cuda ()
refinement = model ( feats , coors , mask , return_type = 1 ) # (2, 32, 3)
coors = coors + refinement # update coors with refinement Esta seção listará os esforços contínuos para tornar a escala do SE3 Transformer um pouco melhor.
Em primeiro lugar, adicionei redes reversíveis. Isso me permite adicionar um pouco mais de profundidade antes de atingir os obstáculos habituais de memória. A preservação da equivariância é demonstrada nos testes.
import torch
from se3_transformer_pytorch import SE3Transformer
model = SE3Transformer (
num_tokens = 20 ,
dim = 32 ,
dim_head = 32 ,
heads = 4 ,
depth = 12 , # 12 layers
input_degrees = 1 ,
num_degrees = 3 ,
output_degrees = 1 ,
reduce_dim_out = True ,
reversible = True # set reversible to True
). cuda ()
atoms = torch . randint ( 0 , 4 , ( 2 , 32 )). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
mask = torch . ones ( 2 , 32 ). bool (). cuda ()
pred = model ( atoms , coors , mask = mask , return_type = 0 )
loss = pred . sum ()
loss . backward () Primeiro instale sidechainnet
$ pip install sidechainnetEm seguida, execute a tarefa de remoção de ruído do backbone da proteína
$ python denoise.py Por padrão, os vetores básicos são armazenados em cache. No entanto, se houver necessidade de limpar o cache, basta definir o sinalizador ambiental CLEAR_CACHE com algum valor ao iniciar o script
$ CLEAR_CACHE=1 python train.pyOu você pode tentar excluir o diretório de cache, que deve existir em
$ rm -rf ~ /.cache.equivariant_attentionVocê também pode designar seu próprio diretório onde deseja que os caches sejam armazenados, caso o diretório padrão possa ter problemas de permissão
CACHE_PATH=./path/to/my/cache python train.py$ python setup.py pytestEsta biblioteca é em grande parte uma versão do repositório oficial de Fabian, mas sem a biblioteca DGL.
@misc { fuchs2020se3transformers ,
title = { SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks } ,
author = { Fabian B. Fuchs and Daniel E. Worrall and Volker Fischer and Max Welling } ,
year = { 2020 } ,
eprint = { 2006.10503 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { satorras2021en ,
title = { E(n) Equivariant Graph Neural Networks } ,
author = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
year = { 2021 } ,
eprint = { 2102.09844 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { gomez2017reversible ,
title = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
author = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
year = { 2017 } ,
eprint = { 1707.04585 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CV }
} @misc { shazeer2019fast ,
title = { Fast Transformer Decoding: One Write-Head is All You Need } ,
author = { Noam Shazeer } ,
year = { 2019 } ,
eprint = { 1911.02150 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.NE }
}