
O apresentador da equipe: Kahraman Kostas
Para começar, reunimos um problema simples para introduzir alguns principais conceitos de posicionamento interno. Considere o seguinte ambiente: um usuário está viajando em espaço aberto na presença de 3 emissores de wifi (chamamos os dados criados por esse usuário de trajetória). Cada emissor tem um endereço MAC exclusivo. O usuário está equipado com um smartphone que examinará periodicamente o ambiente WiFi e gravará o RSSI de cada Mac detectado (em dB).
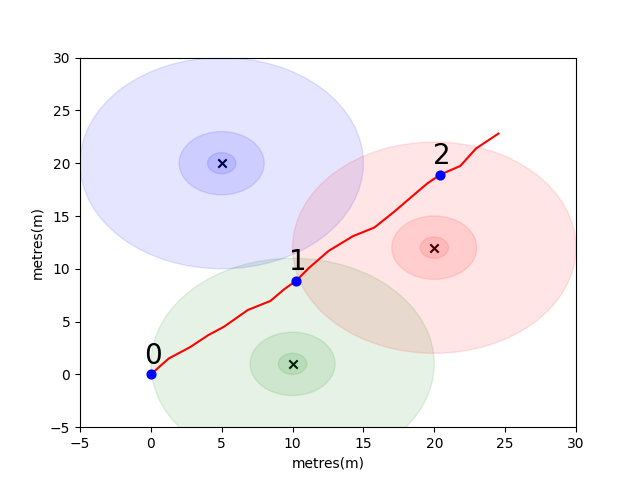
Para este modelo, usamos um modelo de propagação de espaço livre de perda de log padrão para cada um dos emissores. Este é um modelo simplista que funciona bem no espaço livre, mas quebra em ambientes internos reais com paredes e outros obstáculos que podem rejeitar os sinais de uma maneira mais complexa. Em geral, esperamos ver uma queda acentuada no RSSI a distância, à medida que a energia fixa da antena emissora se espalha por uma área crescente à medida que a onda se propaga. No diagrama abaixo de cada círculo indica uma queda de 10dB.
O usuário caminha para o nordeste do ponto (0,0) e lá o telefone faz três varreduras do meio ambiente. Os dados registrados em cada varredura são mostrados abaixo.
scan 0 -> {'green': -60, 'blue': -66, 'red': -67}
scan 1 -> {'green': -58, 'blue': -61, 'red': -60}
scan 2 -> {'green': -66, 'blue': -62, 'red': -59}
As propriedades complexas e localmente únicas do ambiente WiFi o tornam muito útil para sistemas de posicionamento interno. Por exemplo, na imagem abaixo, scan 1 mede os dados aproximadamente no centróide dos três emissores e não há outro lugar nesse ambiente em que se possa fazer uma leitura que registraria valores semelhantes de RSSI. Dado um conjunto de varreduras ou "impressões digitais" de trajetórias independentes, estamos interessados em calcular o quão semelhante eles são no espaço Wi -Fi, pois essa é uma indicação de quão próximos eles estão no espaço real.
Seu primeiro desafio é escrever uma função para calcular a distância euclidiana e as métricas de distância de Manhattan entre cada uma das varreduras na trajetória de amostra que introduzimos acima. Usar os dados de uma única trajetória é uma boa maneira de testar a qualidade de uma métrica de similaridade, pois podemos obter estimativas bastante precisas da distância verdadeira usando os dados da unidade de medição intertal do telefone (IMU), que é usada por um cálculo morto de pedestres Módulo (PDR).
def euclidean ( fp1 , fp2 ):
raise NotImplementedError
def manhattan ( fp1 , fp2 ):
raise NotImplementedError # solution of the above functions
from scipy . spatial import distance
def euclidean ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . euclidean ( fp1 , fp2 )
def manhattan ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . cityblock ( fp1 , fp2 ) import json
import numpy as np
import matplotlib . pyplot as plt
from metrics import eval_dist_metric
with open ( "intro_trajectory_1.json" ) as f :
traj = json . load ( f )
## Pre-calculate the pair indexes we are interested in
keys = []
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
# only calculate the upper triangle
if fp1 [ 'step_index' ] > fp2 [ 'step_index' ]:
keys . append (( fp1 [ 'step_index' ], fp2 [ 'step_index' ]))
## Get the distances from PDR
true_d = {}
for step1 in traj [ 'steps' ]:
for step2 in traj [ 'steps' ]:
key = ( step1 [ 'step_index' ], step2 [ 'step_index' ])
if key in keys :
true_d [ key ] = abs ( step1 [ 'di' ] - step2 [ 'di' ])
euc_d = {}
man_d = {}
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
key = ( fp1 [ 'step_index' ], fp2 [ 'step_index' ])
if key in keys :
euc_d [ key ] = euclidean ( fp1 [ 'profile' ], fp2 [ 'profile' ])
man_d [ key ] = manhattan ( fp1 [ 'profile' ], fp2 [ 'profile' ])
print ( "Euclidean Average Error" )
print ( f' { eval_dist_metric ( euc_d , true_d ):.2f } ' )
print ( "Manhattan Average Error" )
print ( f' { eval_dist_metric ( man_d , true_d ):.2f } ' ) Euclidean Average Error
9.29
Manhattan Average Error
4.90
Se você implementou corretamente as funções, deve ter visto que o erro médio para a métrica euclidiana era 9.29 enquanto o Manhattan era de apenas 4.90 . Portanto, para esses dados, a distância de Manhattan é uma estimativa melhor da verdadeira distância.
É claro que este é um modelo muito simplista. De fato, não há uma relação direta entre os valores do RSSI e a distância do espaço livre dessa maneira. Normalmente, quando criamos nossas próprias estimativas para a distância, usaríamos as distâncias conhecidas de PDR de dentro de uma trajetória para ajustar a pontuação numérica a uma estimativa de distância física.
Para seu principal desafio, gostaríamos que você desenvolvesse sua própria métrica para estimar a distância do mundo real entre duas varreduras, com base apenas em suas impressões digitais de wifi. Forneceremos dados reais de crowdsourcing coletados no início de 2021 em um único shopping. Os dados conterão 114661 digitalizações de impressão digital e 879824 distâncias entre as varreduras. As distâncias serão a nossa melhor estimativa da verdadeira distância, dadas as informações adicionais que levaremos em consideração.
Forneceremos um conjunto de testes de pares de impressões digitais e você precisará escrever uma função que nos diga a que distância eles estão.
Essa função pode ser tão simples quanto uma variação em uma das métricas que introduzimos acima ou tão complexa quanto uma solução completa de aprendizado de máquina que aprende a ponderar diferentes endereços MAC (ou combinações de endereço MAC) de maneira diferente em diferentes situações.
Alguns pontos finais a considerar:
Os dados são montados como três arquivos para você.
O task1_fingerprints.json contém todas as informações de impressão digital para o problema. Essa é cada entrada representa uma varredura real dos emissores de wifi em uma área do shopping. Você descobrirá que os mesmos endereços MAC estarão presentes em muitas das impressões digitais.
O task1_train.csv contém os pares de treinamento válidos para ajudá -lo a projetar/treinar seu algoritmo. Cada par id1-id2 tem uma distância da verdade do solo (em metros) e cada ID corresponde a uma impressão digital do task1_fingerprints.json .
O task1_test.csv é o mesmo formato que task1_train.csv , mas não possui os deslocamentos incluídos. É isso que gostaríamos que você preveja o uso das informações de impressão digital bruta.
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]])Por fim, o modelo ideal deve ser capaz de encontrar um mapeamento exato entre o espaço de impressão digital altamente dimensional (1 impressão digital pode conter muitas medições) e o espaço de distância 1 dimensional. Pode ser útil plotar a distância do PDR (dos dados de treinamento) contra alguma métrica de similaridade computada para ver se a métrica revela uma tendência óbvia. Alta similaridade deve se correlacionar com a baixa distância.
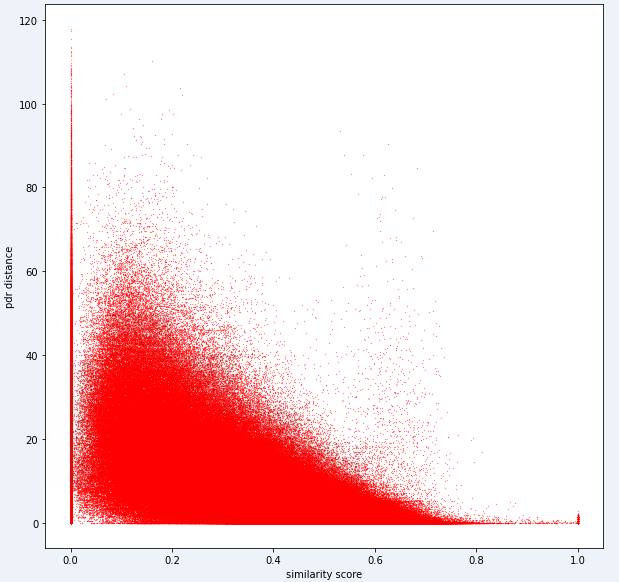
Abaixo está uma métrica de distância que usamos internamente para esta tarefa. Você pode ver que, mesmo para esta métrica, temos uma quantidade considerável de ruído.
Devido a esse nível de ruído, nossa métrica de pontuação para a Tarefa 1 será tendenciosa em relação à precisão sobre a recuperação
Seu envio deve usar os IDs exatos do arquivo test1_test.csv e preencher a terceira coluna de deslocamento (atualmente vazia) com sua distância estimada (em metros) para esse par de impressão digital.
def my_distance_function ( fp1 , fp2 ):
raise NotImplementedError output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
fp1 = fps [ id1 ]
fp2 = fps [ id2 ]
distance_estimate = my_distance_function ( fp1 , fp2 )
output_data . append ([ id1 , id2 , distance_estimate ])
with open ( "MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )As etapas na primeira tarefa podem ser resumidas da seguinte forma.
Essas etapas são ilustradas na imagem abaixo.

Usamos o Python 3.6.5 para criar o arquivo de aplicativo. Incluímos alguns módulos adicionais que não foram incluídos no arquivo de exemplo dado no início da competição. Esses módulos podem ser listados como:
| Mólulos | Tarefa |
|---|---|
| tensorflow | Aprendizado profundo |
| Pandas | Análise de dados |
| Scipy | Computação a distância |
Começamos com a instalação desses módulos como a primeira etapa.
## 1.1 Installing modules
!p ip install tensorflow == 2.6 . 2
!p ip install scipy
!p ip install pandas Nesta etapa, corrigimos a semente aleatória relacionada a ser usada para obter resultados repetíveis. Dessa forma, fornecemos um caminho determinístico em que obtemos o mesmo resultado em todas as execuções. No entanto, de acordo com nossas observações, os resultados obtidos com diferentes computadores podem diferir ligeiramente (± 1%)
## 1.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )
import tensorflow as tf
tf . random . set_seed ( seed_value )
import tensorflow as tf
session_conf = tf . compat . v1 . ConfigProto ( intra_op_parallelism_threads = 1 , inter_op_parallelism_threads = 1 )
sess = tf . compat . v1 . Session ( graph = tf . compat . v1 . get_default_graph (), config = session_conf ) Nesta seção, carregamos os dados que usaremos. Pegamos o código e as explicações do arquivo de amostra fornecido ( Task1-IPS-Challenge-2021.ipynb ).
O task1_fingerprints.json contém todas as informações de impressão digital para o problema. Essa é cada entrada representa uma varredura real dos emissores de wifi em uma área do shopping. Você descobrirá que os mesmos endereços MAC estarão presentes em muitas das impressões digitais.
O task1_train.csv contém os pares de treinamento válidos para ajudá -lo a projetar/treinar seu algoritmo. Cada par id1-id2 tem uma distância da verdade do solo (em metros) e cada ID corresponde a uma impressão digital do task1_fingerprints.json .
O task1_test.csv é o mesmo formato que task1_train.csv , mas não possui os deslocamentos incluídos.
## 1.3 Loading the data
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]]) 879824it [05:16, 2778.31it/s]
5160445it [01:00, 85269.27it/s]
Nesta etapa, realizamos extração de recursos usando duas funções. feature_extraction_file A função simplesmente puxa os valores relevantes das impressões digitais (em pares) do arquivo JSON e as envia para a função feature_extraction para fazer os cálculos.
Na função de feature_extraction , se essas duas impressões digitais forem diferentes uma da outra em termos de tamanho e os dispositivos que eles contêm, todos os dispositivos incluídos nas duas impressões digitais são reunidos para formar uma sequência comum sem repetir. Em cada matriz, tornamos essas duas matrizes idênticas (em termos de dispositivos que eles incluem) atribuindo o valor 0 aos dispositivos não correspondentes. Esse processo é explicado com um exemplo na imagem a seguir.
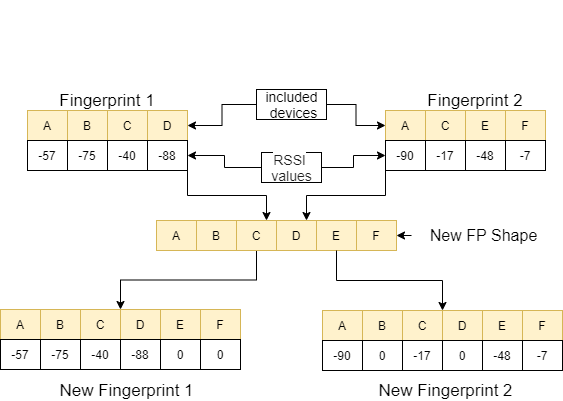
A distância entre essas duas impressões digitais, que são semelhantes, é calculada usando 11 métodos diferentes [1]. Esses métodos são:
Em seguida, esses valores são direcionados para a função feature_extraction_file e salvos como um arquivo CSV nessa função. Em outras palavras, as impressões digitais de vários tamanhos se transformam em um arquivo CSV de 11 recursos como resultado desse processo. O modelo a ser usado é treinado e testado com esses recursos recém -criados.
## 1.4 Feature Extraction
def feature_extraction_file ( data , name , flag ):
features = [[ "braycurtis" ,
"canberra" ,
"chebyshev" ,
"cityblock" ,
"correlation" ,
"cosine" ,
"euclidean" ,
"jensenshannon" ,
"minkowski" ,
"sqeuclidean" ,
"wminkowski" , "real" ]]
for i in tqdm (( data ), position = 0 , leave = True ):
fp1 = fps [ i [ 0 ]]
fp2 = fps [ i [ 1 ]]
feature = feature_extraction ( fp1 , fp2 )
if flag :
feature . append ( i [ 2 ])
else : feature . append ( 0 )
features . append ( feature )
with open ( name , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( features )
#print(features) ## 1.4 Feature Extraction
def feature_extraction ( fp1 , fp2 ):
mac = set ( list ( fp1 . keys ()) + list ( fp2 . keys ()))
mac = { i : 0 for i in mac }
f1 = mac . copy ()
f2 = mac . copy ()
for key in fp1 :
f1 [ key ] = fp1 [ key ]
for key in fp2 :
f2 [ key ] = fp2 [ key ]
f1 = list ( f1 . values ())
f2 = list ( f2 . values ())
braycurtis = scipy . spatial . distance . braycurtis ( f1 , f2 )
canberra = scipy . spatial . distance . canberra ( f1 , f2 )
chebyshev = scipy . spatial . distance . chebyshev ( f1 , f2 )
cityblock = scipy . spatial . distance . cityblock ( f1 , f2 )
correlation = scipy . spatial . distance . correlation ( f1 , f2 )
cosine = scipy . spatial . distance . cosine ( f1 , f2 )
euclidean = scipy . spatial . distance . euclidean ( f1 , f2 )
jensenshannon = scipy . spatial . distance . jensenshannon ( f1 , f2 )
minkowski = scipy . spatial . distance . minkowski ( f1 , f2 )
sqeuclidean = scipy . spatial . distance . sqeuclidean ( f1 , f2 )
wminkowski = scipy . spatial . distance . wminkowski ( f1 , f2 , 1 , np . ones ( len ( f1 )))
output_data = [ braycurtis ,
canberra ,
chebyshev ,
cityblock ,
correlation ,
cosine ,
euclidean ,
jensenshannon ,
minkowski ,
sqeuclidean ,
wminkowski ]
output_data = [ 0 if x != x else x for x in output_data ]
return output_data Nesta tarefa, há impressão digital que têm sinais de RRSI do ambiente de wifi emitores no shopping. O First Challange quer que estimemos a distância entre duas digitalizações de impressões digitais, que é uma tarefa de regressão. Utilizamos Ann (Redes Neurais Artificiais), inspirada na rede neural biológica. Ann consiste em três camadas; Camada de entrada, camadas ocultas (mais de uma) e camada de saída. A RNA inicia com a camada de entrada, que inclui os dados de treinamento (com recursos), passa os dados para a primeira camada oculta, onde os dados são calculados pelos pesos da primeira camada oculta. Nas camadas ocultas, há uma iteração de cálculo de pesos nas entradas e, em seguida, aplica -as uma função de ativação [2]. Como nosso problema é a regressão, nossa última camada é um único neurônio de saída: sua saída é a prevista as distâncias entre pares de varreduras de impressão digital. Nossa primeira camada oculta tem 64 e a segunda tem 128 neurônios. A arquitetura All deste modelo é compartilhada da seguinte maneira. 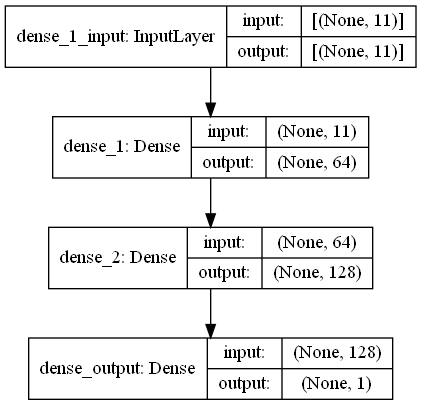
Realizamos o aprendizado profundo usando duas funções. A função create_model molda os dados de treinamento para treinar o modelo e determina a estrutura do modelo. A função model_features produz um modelo com a estrutura especificada. O modelo criado é salvo para ser usado após ser treinado pela função create_model .
## 1.5 Model
import scipy . spatial
import pandas as pd
import numpy as np
import matplotlib . pyplot as plt
from tensorflow import keras
from tensorflow . keras . models import Sequential
from tensorflow . keras . layers import Dense
#from keras.utils.vis_utils import plot_model
% matplotlib inline
def model_features ( i , ii ):
model = Sequential ()
model . add ( Dense ( i , input_shape = ( 11 , ), activation = 'relu' , name = 'dense_1' ))
model . add ( Dense ( ii , activation = 'relu' , name = 'dense_2' ))
model . add ( Dense ( 1 , activation = 'linear' , name = 'dense_output' ))
model . compile ( optimizer = 'adam' , loss = 'mse' , metrics = [ 'mae' ])
model . summary ()
#plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
#print(model.get_config())
return model
def create_model ( name ):
df = pd . read_csv ( name )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X )
y_train = np . array ( df [ df . columns [ - 1 ]])
model = model_features ( 64 , 128 )
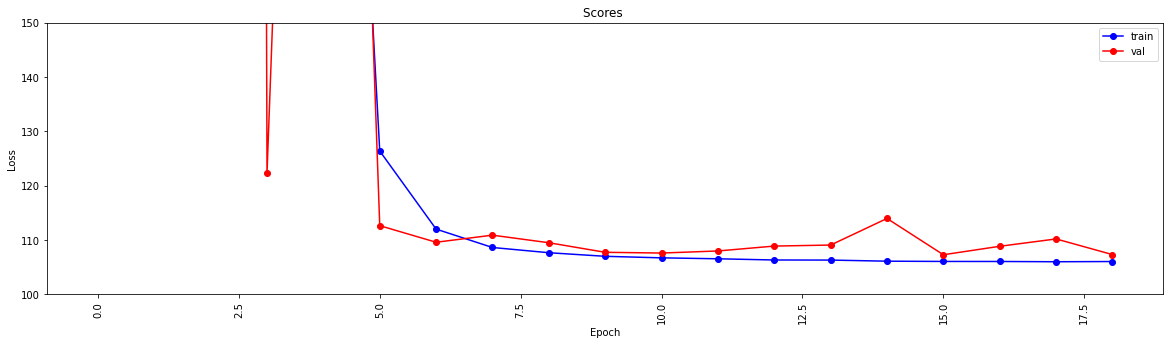
history = model . fit ( X_train , y_train , epochs = 19 , validation_split = 0.5 ) #,batch_size=1)
loss = history . history [ 'loss' ]
val_loss = history . history [ 'val_loss' ]
my_xticks = list ( range ( len ( loss )))
plt . figure ( figsize = ( 20 , 5 ))
plt . plot ( my_xticks , loss , linestyle = '-' , marker = 'o' , color = 'b' , label = "train" )
plt . plot ( my_xticks , val_loss , linestyle = '-' , marker = 'o' , color = 'r' , label = "val" )
plt . title ( "Scores " )
plt . legend ( numpoints = 1 )
plt . ylabel ( "Loss" )
plt . xlabel ( "Epoch" )
plt . xticks ( rotation = 90 )
plt . ylim ([ 100 , 150 ])
plt . show ()
madelname = "./THEMODEL"
model . save ( madelname )
print ( "Model Created!" )
Esta função verifica se os dados de treinamento e teste passaram pela extração de recursos. Caso contrário, cria esses arquivos e o modelo chamando as funções correspondentes. Depois de lidar com o modelo e toda a extração de recursos, ele formata os dados do teste para produzir os resultados finais.
## 1.6 Checking the inputs
from numpy import inf
from numpy import nan
def create_new_files ( train , test ):
model_path = "./THEMODEL/"
my_train_file = 'new_train_features.csv'
my_test_file = 'new_test_features.csv'
if os . path . isfile ( my_train_file ) :
pass
else :
print ( "Please wait! Training data feature extraction is in progress... n it will take about 10 minutes" )
feature_extraction_file ( train , my_train_file , 1 )
print ( "TThe training feature extraction completed!!!" )
if os . path . isfile ( my_test_file ) :
pass
else :
print ( "Please wait! Testing data feature extraction is in progress... n it will take about 100-120 minutes" )
feature_extraction_file ( test , my_test_file , 0 )
print ( "The testing feature extraction completed!!!" )
if os . path . isdir ( model_path ):
pass
else :
print ( "Please wait! Creating the deep learning model... n it will take about 10 minutes" )
create_model ( my_train_file )
print ( "The model file created!!! n n n " )
model = keras . models . load_model ( model_path )
df = pd . read_csv ( my_test_file )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X_train = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X_train )
y_train = np . array ( df [ df . columns [ - 1 ]])
predicted = model . predict ( X_train )
print ( "Please wait! Creating resuşts... " )
return predicted Esta etapa aciona os processos de extração e criação de modelos e permite que todos os processos iniciem. Portanto, usando os IDs do arquivo test1_test.csv , ele preenche a terceira coluna (deslocamento) com a distância estimada para esses pares de impressão digital e salva esse arquivo no diretório com o nome TASK1-MySubmission.csv .
## 1.7 Submission
distance_estimate = create_new_files ( train_data , test_ids )
count = 0
output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
output_data . append ([ id1 , id2 , distance_estimate [ count ][ 0 ]])
count += 1
print ( "Process finished. Preparing result file ..." )
with open ( "TASK1-MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )
print ( "The results are ready. n See MySubmission.csv" ) Please wait! Creating the deep learning model...
it will take about 10 minutes
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 64) 768
_________________________________________________________________
dense_2 (Dense) (None, 128) 8320
_________________________________________________________________
dense_output (Dense) (None, 1) 129
=================================================================
Total params: 9,217
Trainable params: 9,217
Non-trainable params: 0
_________________________________________________________________
Epoch 1/19
13748/13748 [==============================] - 30s 2ms/step - loss: 2007233.6250 - mae: 161.3013 - val_loss: 218.8822 - val_mae: 11.5630
Epoch 2/19
13748/13748 [==============================] - 27s 2ms/step - loss: 24832.6309 - mae: 53.9385 - val_loss: 123437.0859 - val_mae: 307.2885
Epoch 3/19
13748/13748 [==============================] - 26s 2ms/step - loss: 4028.0859 - mae: 29.9960 - val_loss: 3329.2024 - val_mae: 49.9126
Epoch 4/19
13748/13748 [==============================] - 27s 2ms/step - loss: 904.7919 - mae: 17.6284 - val_loss: 122.3358 - val_mae: 6.8169
Epoch 5/19
13748/13748 [==============================] - 25s 2ms/step - loss: 315.7050 - mae: 11.9098 - val_loss: 404.0973 - val_mae: 15.2033
Epoch 6/19
13748/13748 [==============================] - 26s 2ms/step - loss: 126.3843 - mae: 7.8173 - val_loss: 112.6499 - val_mae: 7.6804
Epoch 7/19
13748/13748 [==============================] - 27s 2ms/step - loss: 112.0149 - mae: 7.4220 - val_loss: 109.5987 - val_mae: 7.1964
Epoch 8/19
13748/13748 [==============================] - 26s 2ms/step - loss: 108.6342 - mae: 7.3271 - val_loss: 110.9016 - val_mae: 7.6862
Epoch 9/19
13748/13748 [==============================] - 26s 2ms/step - loss: 107.6721 - mae: 7.2827 - val_loss: 109.5083 - val_mae: 7.5235
Epoch 10/19
13748/13748 [==============================] - 27s 2ms/step - loss: 107.0110 - mae: 7.2290 - val_loss: 107.7498 - val_mae: 7.1105
Epoch 11/19
13748/13748 [==============================] - 29s 2ms/step - loss: 106.7296 - mae: 7.2158 - val_loss: 107.6115 - val_mae: 7.1178
Epoch 12/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.5561 - mae: 7.2039 - val_loss: 107.9937 - val_mae: 6.9932
Epoch 13/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.3344 - mae: 7.1905 - val_loss: 108.8941 - val_mae: 7.4530
Epoch 14/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.3188 - mae: 7.1927 - val_loss: 109.0832 - val_mae: 7.5309
Epoch 15/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.1150 - mae: 7.1829 - val_loss: 113.9741 - val_mae: 7.9496
Epoch 16/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.0676 - mae: 7.1788 - val_loss: 107.2984 - val_mae: 7.2192
Epoch 17/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0614 - mae: 7.1733 - val_loss: 108.8553 - val_mae: 7.4640
Epoch 18/19
13748/13748 [==============================] - 28s 2ms/step - loss: 106.0113 - mae: 7.1790 - val_loss: 110.2068 - val_mae: 7.6562
Epoch 19/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0519 - mae: 7.1791 - val_loss: 107.3276 - val_mae: 7.0981
INFO:tensorflow:Assets written to: ./THEMODELassets
Model Created!
The model file created!!!
Please wait! Creating resuşts...
100%|████████████████████████████████████████████████████████████████████| 5160445/5160445 [00:08<00:00, 610910.29it/s]
Process finished. Preparing result file ...
The results are ready.
See MySubmission.csv
Dado que agora temos uma métrica para avaliar a distância wifi, nossa próxima tarefa é separar as trajetórias de um shopping (um shopping diferente da usada no primeiro desafio!) Nos pisos separados em que eles pertencem. Você pode fazer isso de diferentes maneiras de maneiras diferentes , mas sugeriríamos fortemente uma abordagem de agrupamento de gráficos.
Considere cada impressão digital wifi nos dados como um nó em um gráfico e que podemos formar uma borda com outras impressões digitais no gráfico, avaliando a semelhança com duas impressões digitais. Podemos atribuir um peso alto às bordas, onde temos uma alta semelhança entre as impressões digitais e um baixo peso (ou nenhuma vantagem) entre aqueles que não são semelhantes. Em teoria, uma métrica de similaridade perfeitamente precisa separaria trivialmente pisos, pois poderíamos excluir todas as bordas superiores a 4 metros (aproximadamente a altura de 1 andar de um edifício). Na realidade, é provável que façamos arestas falsas entre os pisos e precisaremos de alguma forma quebrar essas bordas.
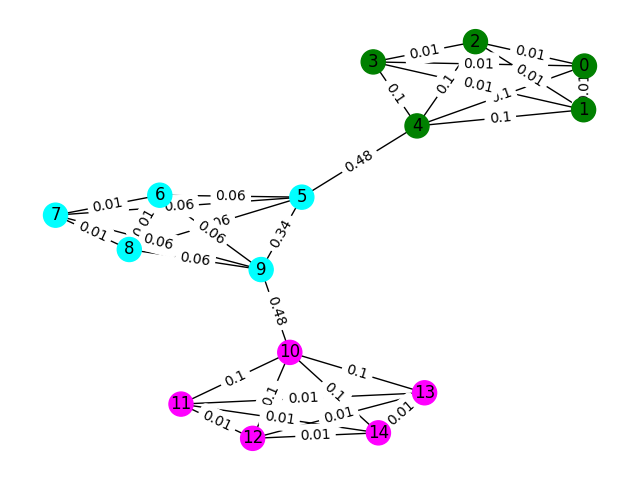
Vamos começar com um exemplo simples. Considere o gráfico abaixo, onde as cores do nó mostram a verdadeira classificação do piso da impressão digital e as bordas refletem que acreditamos que esses nós existem no mesmo andar. Para este exercício, pré-rotulamos cada borda com sua "pontuação entre intermediários", uma métrica que conta quantas vezes essa borda é percorrida, seguindo o caminho mais curto entre dois nós no gráfico. Normalmente, isso revelará arestas que indicam alta conectividade e podem ser candidatos à remoção.
Neste exemplo, use a pontuação de bate-betness para detectar as comunidades do gráfico. Retorne uma lista de listas em que cada sublista contém os IDs dos nó das comunidades. Observe que isso é apenas para ajudar sua compreensão do problema e não conta para a solução real.
def detect_communities ( Graph ):
## This function should return a list of lists containing
## the node ids of the communities that you have detected.
eb_score = nx . edge_betweenness_centrality ( G )
raise NotImplementedError import networkx as nx
from metrics import check_result
G = nx . read_adjlist ( "graph.adjlist" )
communities = detect_communities ( G )
if check_result ( communities ):
print ( "Correct!" )
else :
print ( "Try again" ) Os dados de treinamento de amostra para esse problema são um conjunto de impressões digitais 106981 ( task2_train_fingerprints.json ) e algumas arestas entre elas. Fornecemos arquivos que indicam três tipos de borda diferentes, todos os quais devem ser tratados de maneira diferente.
task2_train_steps.csv indica arestas que conectam as etapas subsequentes dentro de uma trajetória. Essas bordas devem ser altamente confiáveis, pois indicam uma certeza de que duas impressões digitais foram registradas no mesmo andar.
task2_train_elevations.csv indica o oposto das etapas. Essas elevações indicam que as impressões digitais são quase definitivamente de um piso diferente. Você pode assim extrapolar isso se impressão digital
task2_train_estimated_wifi_distances.csv são as distâncias pré-computadas que calculamos usando nossa própria métrica de distância. Essa métrica é imperfeita e, como tal, sabemos que muitas dessas bordas estarão incorretas (ou seja, elas conectarão dois andares). Sugerimos que, inicialmente, você use as arestas neste arquivo para construir seu gráfico inicial e calcular alguma solução. No entanto, se você obtiver uma pontuação alta no Task1, considere calcular suas próprias distâncias de wifi para criar um gráfico.
Seu gráfico pode estar em um dos dois níveis de detalhes, nível de trajetória ou nível de impressão digital, você pode escolher qual representação deseja usar, mas, finalmente, queremos conhecer os clusters de trajetória . O nível de trajetória teria todos os nó como trajetória e bordas entre nós ocorreriam se as impressões digitais em suas trajetórias tivessem alta similiratia. O nível de impressão digital teria cada impressão digital como um nó. Você pode procurar o ID de trajetória da impressão digital usando o task2_train_lookup.json para converter entre representações.
Para ajudá -lo a depurar e treinar sua solução, fornecemos uma verdade fundamental para algumas das trajetórias em task2_train_GT.json . Neste arquivo, as chaves são os IDs de trajetória (o mesmo que no task2_train_lookup.json ) e os valores são o ID de piso real do edifício.
O conjunto de testes é exatamente o mesmo formato que o conjunto de treinamento (para um edifício separado, não facilitaríamos a facilitação;), mas não incluímos o arquivo de verdade do solo equivalente. Isso será retido para nos permitir pontuar sua solução.
Pontos a serem considerados
Nesta seção, forneceremos algum código de exemplo para abrir os arquivos e construir os dois tipos de gráfico.
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/train"
with open ( os . path . join ( path_to_data , "task2_train_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_train_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_train_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_train_lookup.json" )
gt_path = os . path . join ( path_to_data , "task2_train_GT.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f )
with open ( gt_path ) as f :
gt = json . load ( f )
Esta é uma maneira de construir o gráfico de nível de impressão digital, onde cada nó no gráfico é uma impressão digital. Adicionamos pesos de borda que correspondem às distâncias estimadas/verdadeiras das bordas WiFi e PDR, respectivamente. Também adicionamos bordas de elevação para indicar esse relacionamento. Você pode querer fazer explicitamente que não há nenhuma dessas bordas (ou qualquer borda de elevação válida entre as trajetórias) ao desenvolver sua solução.
G = nx . Graph ()
for id1 , id2 , dist in tqdm ( steps ):
G . add_edge ( id1 , id2 , ty = "s" , weight = dist )
for id1 , id2 , dist in tqdm ( wifi ):
G . add_edge ( id1 , id2 , ty = "w" , weight = dist )
for id1 , id2 in tqdm ( elevs ):
G . add_edge ( id1 , id2 , ty = "e" )O gráfico de trajetória não é tão simples quanto você precisa pensar em uma maneira de representar muitas conexões Wi -Fi entre trajetórias. No gráfico de exemplo abaixo, apenas tomamos a distância média como um peso, mas essa é realmente a melhor representação?
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])Seu envio deve ser um arquivo CSV onde as trajetórias que você acredita estar no mesmo andar têm seu índice na mesma linha separada por vírgulas. Cada novo cluster será inserido em uma nova linha.
Por exemplo, consulte a entrada aleatória abaixo.
import random
random_data = []
n_clusters = random . randint ( 50 , 100 )
for i in range ( 0 , n_clusters ):
random_data . append ([])
for traj in set ( fp_lookup . values ()):
cluster = random . randint ( 0 , n_clusters - 1 )
random_data [ cluster ]. append ( traj )
with open ( "MyRandomSubmission.csv" , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( random_data )As etapas da Tarefa 2 podem ser resumidas da seguinte forma:
Node2vec .TASK2-Mysubmission.csv ) é preparado de acordo com a trajetória dos IDs.Essas etapas são ilustradas na imagem abaixo.

Usamos o Python 3.6.5 para criar o arquivo de aplicativo. Incluímos alguns módulos adicionais que não foram incluídos no arquivo de exemplo dado no início da competição. Esses módulos podem ser listados como:
| Mólulos | Tarefa |
|---|---|
| Scikit-Learn | Aprendizado de máquina e preparação de dados |
| node2vec | Aprendizado de recursos escaláveis para redes |
| Numpy | Operações matemáticas |
Começamos com a instalação desses módulos como a primeira etapa.
## 2.1 Installing modules
!p ip install node2vec
!p ip install scikit - learn
!p ip install numpy Nesta etapa, corrigimos a semente aleatória relacionada a ser usada para obter resultados repetíveis. Dessa forma, fornecemos um caminho determinístico em que obtemos o mesmo resultado em todas as execuções. No entanto, de acordo com nossas observações, os resultados obtidos em diferentes computadores podem diferir ligeiramente (± 1%)
## 2.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )Nesta seção, os arquivos fornecidos para os dados de teste são carregados.
wifi leva IDs e pesos do task2_test_estimated_wifi_distances.csv .steps A variável leva IDs e pesos do arquivo task2_test_steps.csv .elevs leva os IDs do arquivo task2_test_elevations.csv .fp_lookup A variável obtém IDs e trajetórias do arquivo task2_test_lookup.json . Não preferimos o método de recalcular as distâncias estimadas dadas no WiFi com o modelo que obtivemos na Task1, porque os resultados obtidos desse processo não fizeram uma diferença significativa. É por isso que não usamos o arquivo task2_test_fingerprints.json em nosso trabalho final.
## 2.3 Loading the data
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/test"
with open ( os . path . join ( path_to_data , "task2_test_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_test_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_test_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_test_lookup.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f ) 3773297it [00:19, 191689.25it/s]
2767it [00:00, 52461.27it/s]
139537it [00:00, 180082.01it/s]
Tomamos a distância média como peso ao criar o gráfico de trajetória. Utilizamos o exemplo dado para a Tarefa 2 ( Task2-IPS-Challenge-2021.ipynb ) para esse processo. Salvamos o gráfico resultante ( B ) como uma lista de adjacência no diretório (como my.adjlist ).
## 2.3 Generating the Trajectory graph.
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])
nx . write_adjlist ( B , "my.adjlist" ) 100%|████████████████████████████████████████████████████████████████████| 3773297/3773297 [00:27<00:00, 135453.95it/s]
100%|██████████████████████████████████████████████████████████████████████████████████████| 2767/2767 [00:00<?, ?it/s]
Antes de fornecer a lista de adjacência como entrada para os algoritmos de aprendizado de máquina, convertemos os nós para o vetor. Em nosso trabalho, usamos a metodologia Node2vec como um algoritmo de incorporação de gráfico proposto por Grover & Leskovec em 2016 [3]. O Node2vec é um algoritmo semi-supervisionado para o aprendizado de recursos dos nós na rede. O node2vec é criado com base na técnica Skip-Gram, que é uma abordagem de PNL motivada no conceito de estrutura de distribuição. De acordo com a idéia, se diferentes palavras usadas em contextos semelhantes, elas provavelmente têm um significado semelhante e há uma relação óbvia entre eles. A técnica Skip-Gram usa a palavra central (entrada) para prever vizinhos (saída) enquanto calcula as probabilidades dos arredores com base em um determinado tamanho da janela (sequência contígua de itens antes do centro), em outras palavras n-gramas. Ao contrário da abordagem PNL, o sistema Node2Vec não é alimentado com palavras que possuem uma estrutura linear, mas nós e bordas, que possuem uma estrutura gráfica distribuída. Essa estrutura multidimensional torna as incorporações complexas e computacionalmente caras, mas o NODE2VEC usa amostragem negativa com otimização de descida de gradiente estocástico (SGD) para lidar com isso. Além disso, a abordagem de caminhada aleatória é usada para detectar os nós vizinhos da amostra do nó de origem em uma estrutura não linear.
Em nosso estudo, primeiro realizamos a representação vetorial das relações de nós no espaço de baixa dimensão modelando com o Node2vec a partir da determinada distância de dois nós (pesos). Em seguida, usamos a saída do Node2vec (Embeddings de gráfico), que possui vetores de nós, para alimentar o algoritmo tradicional de agrupamento de means K.
Os parâmetros que usamos no NOD2VEC podem ser listados da seguinte forma:
| Hiperparâmetro | Valor |
|---|---|
| dimensões | 32 |
| walk_length | 15 |
| Num_walks | 100 |
| trabalhadores | 1 |
| semente | 0 |
| janela | 10 |
| min_count | 1 |
| batch_words | 4 |
O modelo NODE2VEC pega a lista de adjacência como entrada e produz um vetor de 32 tamanho. Nesta parte, o arquivo node.py é criado e executado no Jupyter Notebook . Há duas razões pelas quais é preferível funcionar externamente, e não em uma célula de notebook Jupyter.
Node2vec é um método muito caro computacionalmente, o erro de transbordamento de RAM é bem possível se executar no notebook Jupyter. Criar e executar o modelo Node2vec fora evita esse erro. A célula abaixo cria o arquivo chamado node.py. Este arquivo cria o modelo Node2vec. Este modelo pega a lista de adjacência ( my.adjlist ) como entrada e cria um arquivo de vetor 32-dimensional como saída ( vectors.emb ).
Importante! O código abaixo deve ser executado em distribuições Linux (testadas no Google Colab e Ubuntu).
# 2.4 Converting nodes to vectors
# A folder named tmp is created. This folder is essential for the node2vec model to use less RAM.
try :
if not os . path . exists ( "tmp" ):
os . makedirs ( "tmp" )
except OSError :
print ( "The folder could not be created! n Please manually create the " tmp " folder in the directory" )
node = """
# importing related modules
from node2vec import Node2Vec
import networkx as nx
#importing adjacency list file as B
B = nx.read_adjlist("my.adjlist")
seed_value=0
# Specifying the input and hyperparameters of the node2vec model
node2vec = Node2Vec(B, dimensions=32, walk_length=15, num_walks=100, workers=1,seed=seed_value,temp_folder = './tmp')
#Assigning/specifying random seeds
import os
os.environ['PYTHONHASHSEED']=str(seed_value)
import random
random.seed(seed_value)
import numpy as np
np.random.seed(seed_value)
# creation of the model
model = node2vec.fit(window=10, min_count=1, batch_words=4,seed=seed_value)
# saving the output vector
model.wv.save_word2vec_format("vectors.emb")
# save the model
model.save("vectorMODEL")
"""
f = open ( "node.py" , "w" )
f . write ( node )
f . close ()
! PYTHONHASHSEED = 0 python3 node . py Depois que nosso arquivo vetorial é criado, lemos este arquivo ( vectors.emb ). Este arquivo consiste em 33 colunas. A primeira coluna é o número do nó (IDS) e permanecem são valores de vetor. Ao classificar o arquivo inteiro pela primeira coluna, retornamos os nós ao pedido original. Em seguida, excluímos esta coluna ID, que não usaremos mais. Então, damos a forma final de nossos dados. Nossos dados estão prontos para serem usados em aplicativos de aprendizado de máquina.
# 2.4 Reshaping data
vec = np . loadtxt ( "vectors.emb" , skiprows = 1 )
print ( "shape of vector file: " , vec . shape )
print ( vec )
vec = vec [ vec [:, 0 ]. argsort ()];
vec = vec [ 0 : vec . shape [ 0 ], 1 : vec . shape [ 1 ]] shape of vector file: (11162, 33)
[[ 9.1200000e+03 3.9031842e-01 -4.7147268e-01 ... -5.7490986e-02
1.3059708e-01 -5.4280665e-02]
[ 6.5320000e+03 -3.5591956e-02 -9.8558587e-01 ... -2.7217887e-02
5.6435770e-01 -5.7787680e-01]
[ 5.6580000e+03 3.5879680e-01 -4.7564098e-01 ... -9.7607370e-02
1.5506668e-01 1.1333219e-01]
...
[ 2.7950000e+03 1.1724627e-02 1.0272172e-02 ... -4.5596390e-04
-1.1507459e-02 -7.6738600e-04]
[ 4.3380000e+03 1.2865483e-02 1.2103912e-02 ... 1.6619096e-03
1.3672550e-02 1.4605848e-02]
[ 1.1770000e+03 -1.3707868e-03 1.5238028e-02 ... -5.9994194e-04
-1.2986251e-02 1.3706315e-03]]
Task-2 é um problema de agrupamento. A premissa que precisamos decidir ao resolver esse problema é quantos clusters devemos dividir. Para isso, tentamos números de cluster diferentes e comparamos as pontuações que obtivemos. O gráfico abaixo mostra a comparação do número de clusters e a pontuação obtida. Como pode ser visto neste gráfico, o número de clusters aumentou continuamente entre 5 e 21, com algumas flutuações de exceção, e estabilizado após 21. Por esse motivo, focamos no número de aglomerados entre 21 e 23 em nosso estudo.
# 2.5 Determine the number of clusters
import numpy as np
import matplotlib . pyplot as plt
import seaborn as sns
import matplotlib
% matplotlib inline
sns . set_style ( "whitegrid" )
agglom = [ 24.69 , 28.14 , 28.14 , 28.14 , 30 , 33.33 , 40.88 , 38.70 , 40 , 40 , 40 , 29.12 , 45.85 , 45.85 , 48.00 , 50.17 , 57.83 , 57.83 , 57.83 ]
plt . figure ( figsize = ( 10 , 5 ))
plt . plot ( range ( 5 , 24 ), agglom )
matplotlib . pyplot . xticks ( range ( 5 , 24 ))
plt . title ( 'Number of clusters and performance relationship' )
plt . xlabel ( 'Number of clusters' )
plt . ylabel ( 'Score' )
plt . show ()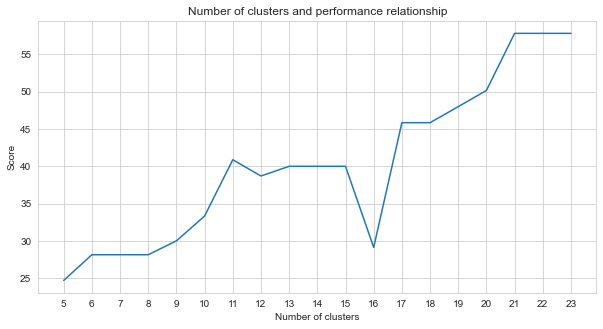
Entre os métodos não supervisionados de aprendizado de máquina que tentamos (como K-Means, aglomeramento aglomerativo, propagação de afinidade, mudança média, agrupamento espectral, dbscan, óptica, birch, mini-lotes k-means), alcançamos os melhores resultados usando k-means com 23 clusters.
O K-Means é um algoritmo de agrupamento é uma das técnicas básicas e tradicionais de aprendizado de máquina não supervisionado que fazem suposições para encontrar grupos de elementos homogêneos ou naturais (clusters) usando dados não marcados. Os clusters devem definir pontos (nós em nossos dados) agrupados que compartilham semelhanças particulares. O K-Means precisa do número alvo de centróides, que se refere a quantos grupos os dados devem ser divididos. O algoritmo começa com o grupo de centróides designados aleatoriamente e continua as iterações para encontrar as melhores posições deles. O algoritmo atribui os pontos/nós aos centróides designados usando em cluster a soma dos quadrados do membro de pontos, isso continua atualizando e se mudando [4]. Em nosso exemplo, o número de centróides reflete o número de pisos. Deve -se notar que isso não fornece informações sobre a ordem dos pisos.
Abaixo, a aplicação K-Means foi feita para 23 clusters.
# 2.5 Best result
from sklearn import cluster
import time
ML_results = []
k_clusters = 23
algorithms = {}
algorithms [ 'KMeans' ] = cluster . KMeans ( n_clusters = k_clusters , random_state = 10 )
second = time . time ()
for model in algorithms . values ():
model . fit ( vec )
ML_results = list ( model . labels_ )
print ( model , time . time () - second ) KMeans(n_clusters=23, random_state=10) 1.082334280014038
A saída do algoritmo de aprendizado de máquina determina a qual cluster as impressões digitais pertencem. Mas o que é exigido de nós é agrupar as trajetórias. Portanto, essas impressões digitais são convertidas em suas contrapartes de trajetória usando a variável fp_lookup . Esta saída é processada no arquivo TASK2-Mysubmission.csv .
## 2.6 Submission
result = {}
for ii , i in enumerate ( set ( fp_lookup . values ())):
result [ i ] = ML_results [ ii ]
ters = {}
for i in result :
if result [ i ] not in ters :
ters [ result [ i ]] = []
ters [ result [ i ]]. append ( i )
else :
ters [ result [ i ]]. append ( i )
final_results = []
for i in ters :
final_results . append ( ters [ i ])
name = "TASK2-Mysubmission.csv"
with open ( name , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( final_results )
print ( name , "file is ready!" ) TASK2-Mysubmission.csv file is ready!
[1] P. Virtanen e Scipy 1.0 Contribuidores. SCIPY 1.0: Algoritmos fundamentais para computação científica em Python. Nature Methods, 17: 261--272, 2020.
[2] A. Geron, aprendizado de máquina prático com scikit-learn, keras e tensorflow: conceitos, ferramentas e técnicas para criar sistemas inteligentes. O'Reilly Media, 2019
[3] A. Grover, J. Leskovec. Conferência Internacional da ACM Sigkdd sobre Descoberta do Conhecimento e Mineração de Dados (KDD), 2016.
[4] Jin X., Han J. (2011) Clustering K-Means. In: Sammut C., Enciclopédia de Webb GI (eds) do aprendizado de máquina. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-30164-8_425