Noise Reduction
1.0.0
Sobre o projeto
Pilha de tecnologia
Estrutura de arquivo
Começando
Resultados e demonstração
Trabalho futuro
Colaboradores
Agradecimentos e recursos
Licença
O ruído precisava ser removido, que é naturalmente induzido como o ruído não ambiental que é removido com o denoização do sinal. Consulte esta documentação também este blog sobre redução de ruído da AI
A biblioteca Librosa para manupulação de áudio é usada.
Para os sinais de áudio, usamos o Scipy
Matplotlib usado para manipular os dados e visualizar o sinal.
O restante é Numpy para operações matemáticas, onda para a operação no arquivo de onda.
Noise Reduction ├───docs ## Documents and Images │ └───Input Audio file ├─── Project Details │ | │ ├─── │ │ ├───Research papers │ │ ├───Linear Algebra │ │ ├───Neural networks & Deep Learning │ │ ├───Project Documentation │ │ ├───AI Noise Reduction Blog │ │ ├───AI Noise Reduction Report │ │ └───Code Implementation │ │ ├───AI Noise Reduction.py │ │ ├───audio.wav │ │ ├───Resources
Testado no Windows
clone git https://github.com/dhriti03/noise-ducuction.gitcd ruído- redução
No seu caderno, instale certas bibliotecas
PiP Install Wave pip install librosa pip install scipy.io pip install matplotlib.pyplot
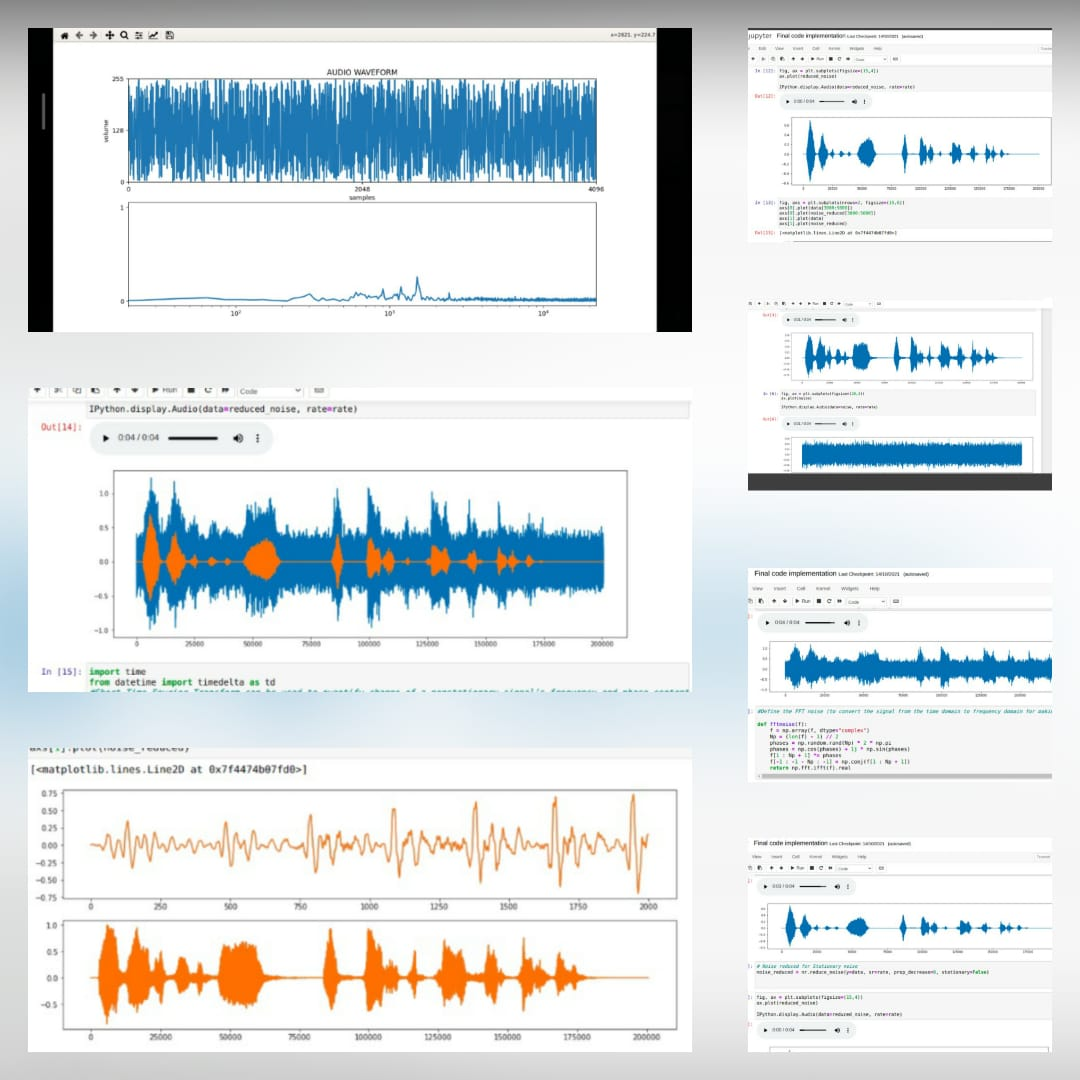
*Este é o arquivo de áudio original *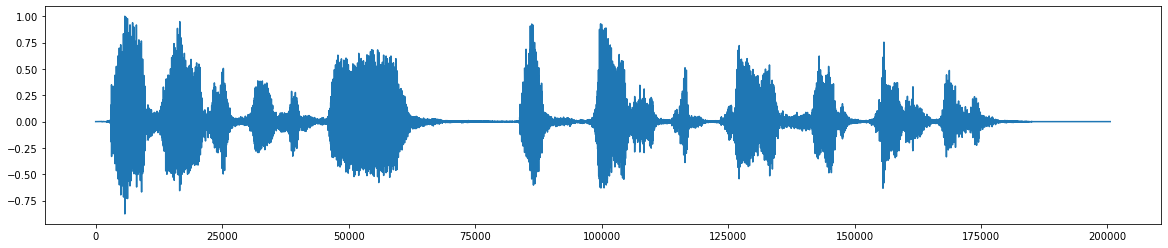 
*Após a adição do ruído * 
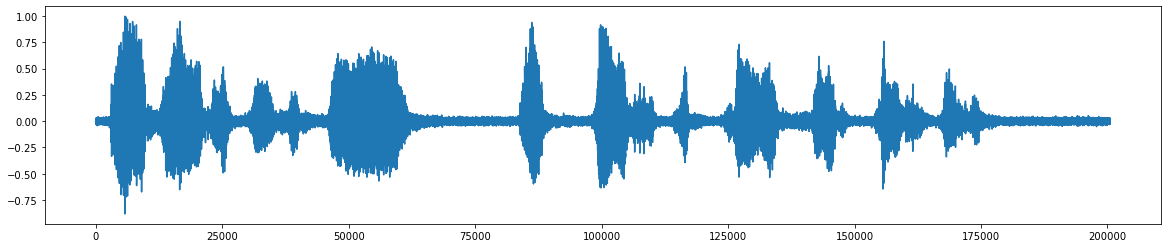*O sinal de áudio final após remover o ruído * 
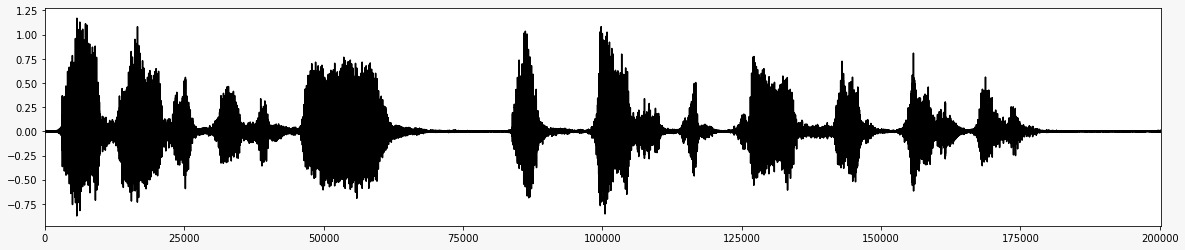*Fluxograma para o projeto *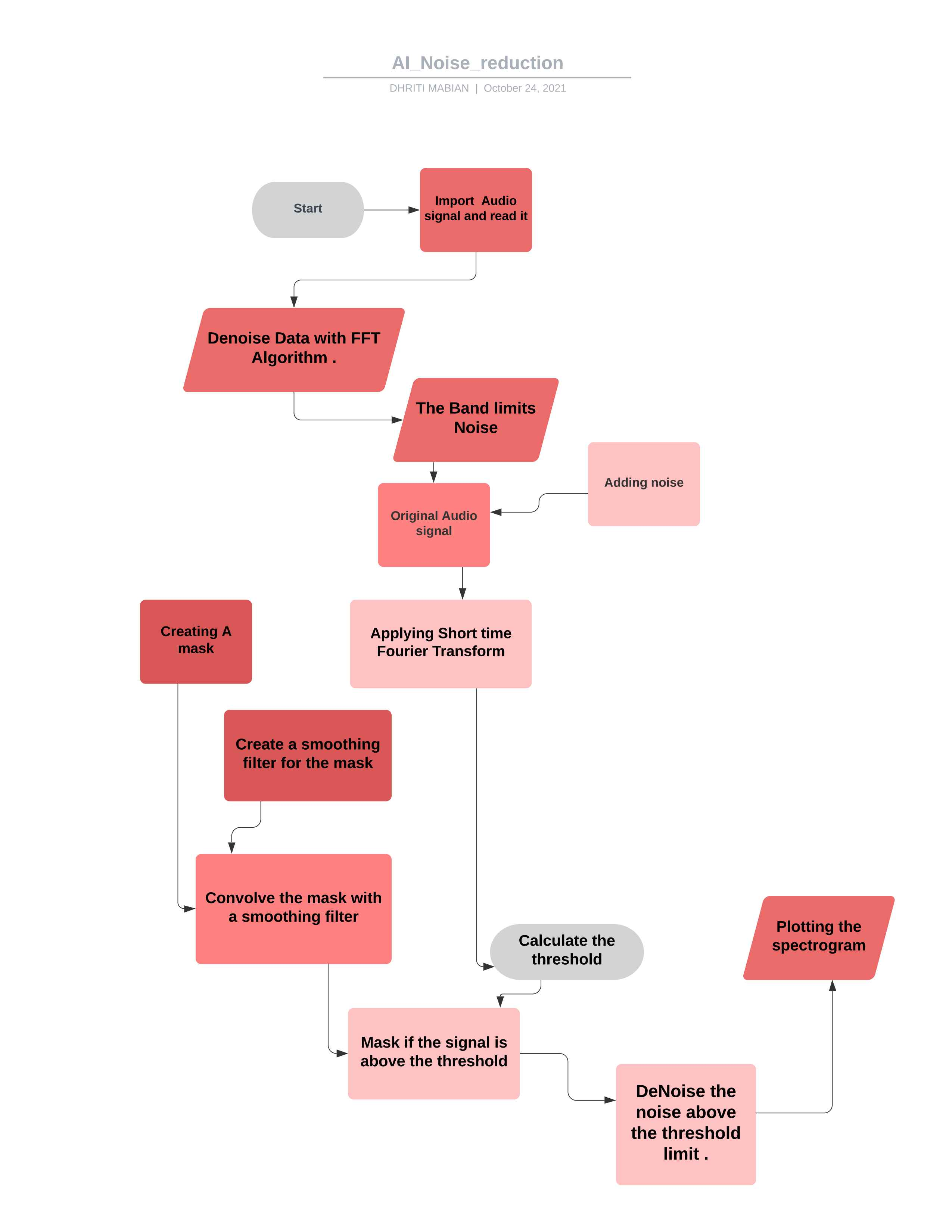 
Ao manipular o código de acordo com seus requisitos, você pode usá -lo para controlar a maioria dos sinais de áudio. ##Teoria
Um FFT é calculado sobre o clipe de áudio de ruído
As estatísticas são calculadas sobre a FFT do ruído (em frequência)
Um limite é calculado com base nas estatísticas do ruído (e na sensibilidade desejada do algoritmo)
Uma máscara é determinada comparando o sinal FFT com o limite
A máscara é suavizada com um filtro sobre a frequência e o tempo
A máscara é aplicada à FFT do sinal e é invertida
Importar ipython do scipy.io importar wavfileimport scipy.signalimport numpy como npimport matplotlib.pyplot como plimport librosaimport onda%matplotlib inline
Aqui estamos importando as bibliotecas como a libra ipython usada para criar um ambiente abrangente para a computação interativa e exploratória.
Na biblioteca Scipy.io , é usada para manipular os dados e a visualização dos dados usando uma ampla gama de comandos Python.
O Numpy contém uma matriz multidimensional e estruturas de dados da matriz. Pode ser utilizado para executar várias operações matemáticas em matrizes como rotinas trigonométricas, estatísticas e algébricas, portanto, é uma biblioteca muito útil.
A biblioteca Matplotlib.pyplot ajuda a entender a enorme quantidade de dados por meio de diferentes visualizações.
Librosa usada quando trabalhamos com dados de áudio como na geração de música (usando o LSTM's), reconhecimento automático de fala. Ele fornece os blocos de construção necessários para criar os sistemas de recuperação de informações musicais.
%Matplotlib inline para ativar a plotagem embutida, onde as plotagens/gráficos serão exibidas logo abaixo da célula onde seus comandos de plotagem são gravados. Ele fornece interatividade com o back -end no frontend, como o notebook Jupyter.
wav_loc = r '/home/ruído_redution/downloads/onda/file.wav'rate, dados = wavfile.read (wav_loc, mmap = false)
Aqui, pegamos o local do caminho do arquivo waw e, em seguida, lemos o arquivo waw com o módulo Wavefile , que é da biblioteca Scipy.io . com parâmetros (nome do arquivo - string ou interno de arquivo, que é um arquivo WAV de entrada.) Então o (mmap: bool, opcional, no qual leia os dados como mapeados de memória (padrão: false).
def fftnoise (f): f = np.array (f, dtype = "complex") np = (len (f) - 1) // 2fases = np.random.rand (np) * 2 * np.piphases = np .Cos (fases) + 1J * np.sin (fases) f [1: np + 1] * = phasesf [-1: -1 -np: -1] = np.conj (f [1: np + 1] ) retornar np.fft.ifft (f) .real
Aqui, definimos primeiro a função de ruído da FFT em breve, uma transformação rápida de Fourier (FFT) é um algoritmo que calcula a transformação discreta de Fourier (DFT) de uma sequência ou seu inverso (IDFT). A análise de Fourier converte um sinal de seu domínio original (geralmente tempo ou espaço) em uma representação no domínio da frequência e vice -versa. A DFT é obtida decompondo uma sequência de valores em componentes de diferentes frequências.
Usando a transformação rápida de Fourier e definindo uma função do complexo do tipo de dados e, finalmente, calculando a parte real da função. Nisso, as freqências que variam entre a frequência mínima e a frequência máxima são definidas como 1 e são negligenciadas indesejadas.
Dando o local do arquivo
Lendo o arquivo WAV
-32767 a +32767 é um áudio adequado (para ser simétrico) e 32768 significa que o áudio preso nesse ponto
O arquivo wav é de 16 bits, o intervalo é [-32768, 32767], dividindo-se assim por 32768 (2^15) fornecerá a faixa de complemento apropriada de [-1, 1]
def band_limited_noise (min_freq, max_freq, amostras = 1024, samplerate = 1): freqs = np.abs (np.fft.fftfreq (amostras, 1 / samplerate)) f = np.zeros (amostras) f [np.Logical_and (freeqs)) > = min_freq, Freqs <= max_freq)] = 1rendurn fftnoise (f)
Uma função ou série temporal cuja transformação de Fourier é restrita a uma gama finita de frequências ou comprimentos de onda.
Definindo o Freq com o Freq padrão com o limite MIN e Max.
ruído_len = 2 # SecondSnoise = band_limited_noise (min_freq = 4000, max_freq = 12000, amostras = len (dados), sampleate = rate)*10noise_clip = ruído [: taxa*ruído_len] audio_clip_band_bland = dados+ruído
O bloco de ruído branco limitado por banda especifica um espectro de dois lados, onde as unidades são Hz.
onde o máximo de 12000 e o Min Freq de 4000 é comparado a WRT o ruído e os dados fornecidos.
Aqui estamos cortando o sinal de ruído tendo um produto da taxa e o len do sinal de ruído.
adicionando assim o ruído e os dados fornecidos
Com efeito, a adição de ruído expande o tamanho do conjunto de dados de treinamento.
O ruído aleatório é adicionado às variáveis de entrada, tornando -as diferentes toda vez que são expostas ao modelo.
Adicionar ruído às amostras de entrada é uma forma simples de aumento de dados.
Adicionar ruído significa que a rede é menos capaz de memorizar amostras de treinamento porque elas estão mudando o tempo todo,
resultando em pesos de rede menores e em uma rede mais robusta que possui menor erro de generalização.
Importar tempo de importação de dados Timedelta como TD
Tempo de importação Este módulo fornece várias funções relacionadas ao tempo. Para funcionalidade relacionada, consulte também os módulos DateTime e Calendário. classe DateTime.timedelta
Uma duração expressando a diferença entre duas instâncias de data, hora ou datetime para resolução de microssegundos.
def _stft (y, n_fft, hop_length, win_length): retorna librosa.stft (y = y, n_fft = n_fft, hop_length = hop_length, win_length = win_length)
A transformação de Fourier de curto período de tempo pode ser usada para quantificar a alteração da frequência de um sinal não estacionário e o conteúdo de fase ao longo do tempo.
O comprimento do salto deve se referir ao número de amostras entre quadros sucessivos. Para análise de sinal, o comprimento do salto deve ser menor que o tamanho do quadro, para que os quadros se sobreponham.
Parâmetros ynp.ndary [shape = (n,)], sinal de entrada com valor real
n_fftint> 0 [escalar]
comprimento do sinal de janela após preenchimento com zeros. O número de linhas na matriz STFT D é (1 + n_fft/2) . O valor padrão, n_fft = 2048 amostras, corresponde a uma duração física de 93 milissegundos a uma taxa de amostragem de 22050 Hz, ou seja, a taxa de amostragem padrão em Librosa. Este valor está bem adaptado para sinais musicais. No entanto, no processamento da fala, o valor recomendado é 512, correspondendo a 23 milissegundos a uma taxa de amostragem de 22050 Hz. De qualquer forma, recomendamos definir o N_FFT para um poder de dois para otimizar a velocidade do algoritmo Fast Fourier Transform (FFT).
hop_lengthint> 0 [escalar]
Número de amostras de áudio entre colunas STFT adjacentes.
Os valores menores aumentam o número de colunas em D sem afetar a resolução de frequência do STFT.
Se não especificado, os padrões para win_length // 4 (veja abaixo).
win_lengthint <= n_fft [escalar]
Cada quadro de áudio é janela por janela de comprimento win_length e depois acolchoado com zeros para corresponder a N_FFT .
Os valores menores melhoram a resolução temporal do STFT (ou seja, a capacidade de discriminar impulsos que estão intimamente espaçados no tempo) às custas da resolução de frequência (ou seja, a capacidade de discriminar tons puros que estão intimamente espaçados em frequência). Esse efeito é conhecido como trade-off de localização de frequência de tempo e precisa ser ajustado de acordo com as propriedades do sinal de entrada y.
Se não especificado, os padrões de win_length = n_fft .
Retornar Librosa.istft (y, hop_length, win_length)
Transformação inversa de Fourier de curto tempo (ISTFT) .Converta espectrograma com valor complexo stft_matrix para séries temporais y minimizando o erro médio quadrado entre stft_matrix e stft de y, conforme descrito em
Em geral, a função da janela, o comprimento do salto e outros parâmetros devem ser os mesmos do STFT, o que leva principalmente à reconstrução perfeita de um sinal da STFT_MATRIX não modificada.
def _amp_to_db (x): return librosa.core.amplitude_to_db (x, ref = 1.0, Amin = 1e-20, top_db = 80.0)
1.Converta um espectrograma de amplitude para espectrograma com escala de DB.Este equivalente a Power_TO_DB (S ** 2), mas é fornecido por conveniência.
Retornar Librosa.core.db_to_amplitude (x, ref = 1.0)
Converta um espectrograma com escala de DB em um espectrograma de amplitude.
Isso inverte efetivamente amplitude_to_db:
db_to_amplitude (s_db) ~ = 10,0 (0,5* (s_db + log10 (ref)/10)) **
def plot_spectrograma (sinal, título): fig, ax = plt.sublots (figSize = (20, 4)) cax = ax.matshow (sinal, origem = "inferior", aspecto = "auto", cmap = plt.cm. sísmico, vmin = -1 * np.max (np.abs (sinalizador)), vmax = np.max (np.abs (signal)),
)Plotando o espetcograma com sinal como entrada.
A classe Axes contém a maioria dos elementos da figura: eixo, carrapato, linha2d, texto, polígono, etc., e define o sistema de coordenadas.
Ele fornece vários mapas de cores no matplotlib acessível por meio desta função .O Encontre uma boa representação no espaço de cores 3D para o seu conjunto de dados.
Fig.Colorbar (Cax) ax.set_title (título)
A melhor maneira de ver o que está acontecendo é adicionar uma barra colorida (plt.colorbar (), depois de criar o gráfico de dispersão). Você notará que seus valores fora entre 0 e 10000 estão todos abaixo da parte mais baixa da barra, onde as coisas são um verde muito claro.
Em geral, os valores abaixo do VMIN serão coloridos com a cor mais baixa e os valores acima do VMAX terão a cor mais alta.
Se você definir o Vmax menor que o VMIN, eles serão trocados internamente. Embora, dependendo da versão exata do matplotlib e das funções precisas chamadas, o Matplotlib pode dar um aviso de erro. Portanto, é melhor definir o VMIN sempre menor que o Vmax.
def plot_statistics_and_filter (mean_freq_noise, std_freq_noise, ruído_thresh, smoothing_filter): fig, ax = plt.subplots (ncols = 2, figSize = (20, 4))) de barulho ")
plt_std, = ax [0] .Plot (ruído_thresh, label = "limiar de ruído (por frequência)") ax [0] .set_title ("limiar para máscara")
ax [0] .legend () cax = ax [1] .matshow (smoothing_filter, origem = "inferior") fig.colorbar (cax) ax [1] .set_title ("filtro para suavizar a máscara")Plota estatísticas básicas da redução de ruído.
A relação sinal/ruído (SNR ou S/N) é uma medida usada na ciência e engenharia que compara o nível de um sinal desejado com o nível de ruído de fundo.
O SNR é definido como a razão entre a potência do sinal e a potência do ruído, geralmente expressa em decibéis.
Uma razão superior a 1: 1 (maior que 0 dB) indica mais sinal que ruído.
Configurando a frequência de limiar para o mascaramento de ruído.
O limiar de mascaramento refere -se a um processo em que um som é tornado inaudível devido à presença de outro som.
Portanto, o limiar de mascaramento é o nível de pressão sonora de um som necessário para tornar o som audível na presença de outro ruído chamado "mascarador"
assim adicionou o limiar.
Sinais de ruído desfoque com vários filtros de passagem baixa
Aplicar filtros personalizados às imagens (convolução 2D)
def removeloise ( # para calcular a média do sinal (tensão) da porção de inclinação positiva (ascensão) de uma onda de triângulo para tentar remover o máximo de ruído possível. Audio_clip, # Esses clipes são os parâmetros usados nos quais faríamos os respectivos respectivos Operações ruído_clip, n_grad_freq = 2, # quantos canais de frequência suavizaram com o mask.n_grad_time = 4, # quantos canais de tempo suavizaram com o máscara.n_fft = 2048, # Número de áudio de quadros entre stft columns.win_length = 2048, # Cada quadro de áudio é janela por `Window ()`. n_std_thresh = 1.5, # quantos desvios padrão mais alto que o db médio do ruído (em cada nível de frequência) a ser considerado sinalizadorprop_decrease = 1.0, # em que medida você deve diminuir o ruído (1 = all, 0 = nenhum) verbose = false = false , # Flag permite que você escreva expressões regulares que pareçam apresentáveisVisual = false, # se plotar as etapas do algoritmo):
def Removeloise ( para média o sinal (tensão) da porção de inclinação positiva (aumento) de uma onda de triângulo para tentar remover o máximo de ruído possível.
AUDIO_CLIP,
Esses clipes são os parâmetros usados nos quais faríamos as respectivas operações
ruído_clip, n_grad_freq = 2 Quantos canais de frequência suavizar com a máscara.
n_grad_time = 4, quantos canais de tempo suavizaram com a máscara.
n_fft = 2048
Número de áudio de quadros entre as colunas STFT.
win_length = 2048, cada quadro de áudio é janela por window() . A janela será de comprimento win_length e depois acolchoada com zeros para combinar com n_fft ..
hop_length = 512, número de áudio de quadros entre as colunas STFT.
n_std_thresh = 1.5 Quantos desvios padrão mais alto que o db médio do ruído (em cada nível de frequência) a ser considerado sinal
prop_decrease = 1.0, até que ponto você deve diminuir o ruído (1 = tudo, 0 = nenhum)
verbose = false,
A Flag permite que você escreva expressões regulares que parecem apresentáveis visuais = false, #se plotar as etapas do algoritmo):
ruído_stft = _stft (ruído_clip, n_fft, hop_length, win_length) ruído_stft_db = _amp_to_db (np.abs (ruído_stft))
Stft sobre ruído
converter em db
mean_freq_noise = np.mean (ruído_stft_db, exis = 1) std_freq_noise = np.std (ruído_stft_db, exis = 1) ruir_thresh = mean_freq_noise + std_freq_noise * n_st_thhsh
Calcule estatísticas sobre ruído
Aqui, para o ruído de Thresh, adicionamos a média e o ruído padrão e o ruído n_std.
sig_stft = _stft (audio_clip, n_fft, hop_length, win_length) sig_stft_db = _amp_to_db (np.abs (sig_stft))
STFT Over Signal
mask_gain_db = np.min (_amp_to_db (np.abs (sig_stft)))
Calcule o valor para mascarar o db para
smoothing_filter = np.outer (np.concatenate (
[np.linspace (0, 1, n_grad_freq + 1, endpoint = false), np.linspace (1, 0, n_grad_freq + 2),
]
) [1: -1], np.concatenate (
[np.linspace (0, 1, n_grad_time + 1, endpoint = false), np.linspace (1, 0, n_grad_time + 2),
]
) [1: -1],
) Smoothing_filter = Smoothing_filter / np.sum (Smoothing_filter)Crie um filtro de suavização para a máscara no tempo e na frequência
db_thresh = np.repeat (np.rehape (ruído_thresh, [1, len (mean_freq_noise)]), np.shape (sig_stft_db) [1], eixo = 0,
) .TCalcule o limite para cada compartimento de frequência/tempo
sig_mask = sig_stft_db <db_thresh
máscara para o sinal
sig_mask = scipy.signal.fftconvolve (sig_mask, smoothing_filter, mode = "mesmo") sig_mask = sig_mask * prop_decrease
Máscara de convolução com filtro de suavizamento
# mask the signalsig_stft_db_masked = (sig_stft_db * (1 - sig_mask)+ np.ones(np.shape(mask_gain_dB)) * mask_gain_dB * sig_mask) # mask realsig_imag_masked = np.imag(sig_stft) * (1 - sig_mask)sig_stft_amp = (_db_to_amp (SIG_STFT_DB_MASKED) * NP.SIGN (SIG_STFT)) + (1J * SIG_IMAG_MASKED)
Mascarar o sinal
# Recupere o Signalrecovered_signal = _istft (sig_stft_amp, hop_length, win_length) recuperado_spec = _amp_to_db (np.abs (_stft (recuperado_signal, n_fft, hop_length, win_length)
)recuperar o sinal
Assim, aplique máscara se o sinal estiver acima do limite
Convidar a máscara com um filtro de suavização
Aplicando o algorithum de redução de ruído para o arquivo WAV já baixado.
Aplicando o FFT na gravação ao vivo do sinal de áudio.
Mais uma implementação mais profunda da IA para o cancelamento de ruído.
Aplicando o algorithum de redução de ruído para vários formatos de arquivos de áudio.
O sinal de áudio ao vivo com o microfone e o ESP32 e, portanto, obterá o arquivo WAV para obter mais computação e processamento de sinal.
Dhriti Mabian
Priyal Awankar
*SRA VJTI_EKLAVYA 2021
Shreyas atre
Shah duro
Audácia
Método de cancelamento de ruído
Pegou o caldeira de Martin Heinz
Tim Sainburg
Licença
