O teste de equivalência pode ser aplicado para avaliar se um efeito observado de um preditor individual em um modelo de regressão múltipla é pequeno o suficiente para ser considerado estatisticamente e praticamente insignificante (Alter & Counsell, 2021). Para mais informações, consulte a página OSF e/ou uma pré -impressão disponível gratuitamente no Psyarxiv.
As funções a seguir oferecem alternativas baseadas em equivalência apropriadas para concluir o efeito insignificante entre um preditor e o resultado em regressão múltipla
Essas funções R são projetadas para acomodar vários contextos de pesquisa sem esforço, com ou sem acesso ao conjunto de dados completo. As duas funções, reg.equiv.fd() e reg.equiv() , fornecem saída semelhante, mas diferem no tipo de informação de entrada exigida pelo usuário.
Especificamente, a primeira função, reg.equiv.fd() , requer o conjunto de dados e o modelo completo em r (objeto lm ), enquanto o segundo não. O reg.equiv() destina -se a pesquisadores que não têm acesso ao conjunto de dados completo, mas ainda desejam avaliar a falta de associação de um determinado preditor com a variável de resultado em regressão múltipla, por exemplo, usando informações normalmente apresentadas em uma seção de resultados ou Tabela relatada em um artigo publicado.
reg.equiv.fd() : conjunto de dados completo necessáriodatfra= um quadro de dados (por exemplo, mtcars)model= o modelo, um objeto LM (por exemplo, mod1 , onde mod1<- mpg~hp+cyl )delta= o menor tamanho de efeito de interesse (sesoi), tamanho de efeito minimamente significativo (MMES) ou limite superior do intervalo de equivalência (?) (Por exemplo, .15)predictor= o nome do preditor a ser testado (por exemplo, "cyl" )test= Tipo de teste é definido automaticamente para dois testes unilaterais (Tost; Schuirmann, 1987), a outra opção é o Anderson-Hauck (AH; Anderson & Hauck, 1983)std= o delta (ou, sesoi) é o conjunto conforme padronizado por padrão. Indicar std=FALSE para assumir unidades não padronizadasalpha= A taxa de erro nominal do tipo I é definida como 0,05 por padrão. Para mudar, basta indicar o nível alfa. Por exemplo, alpha=.10 reg.equiv.fd() Exemplo: 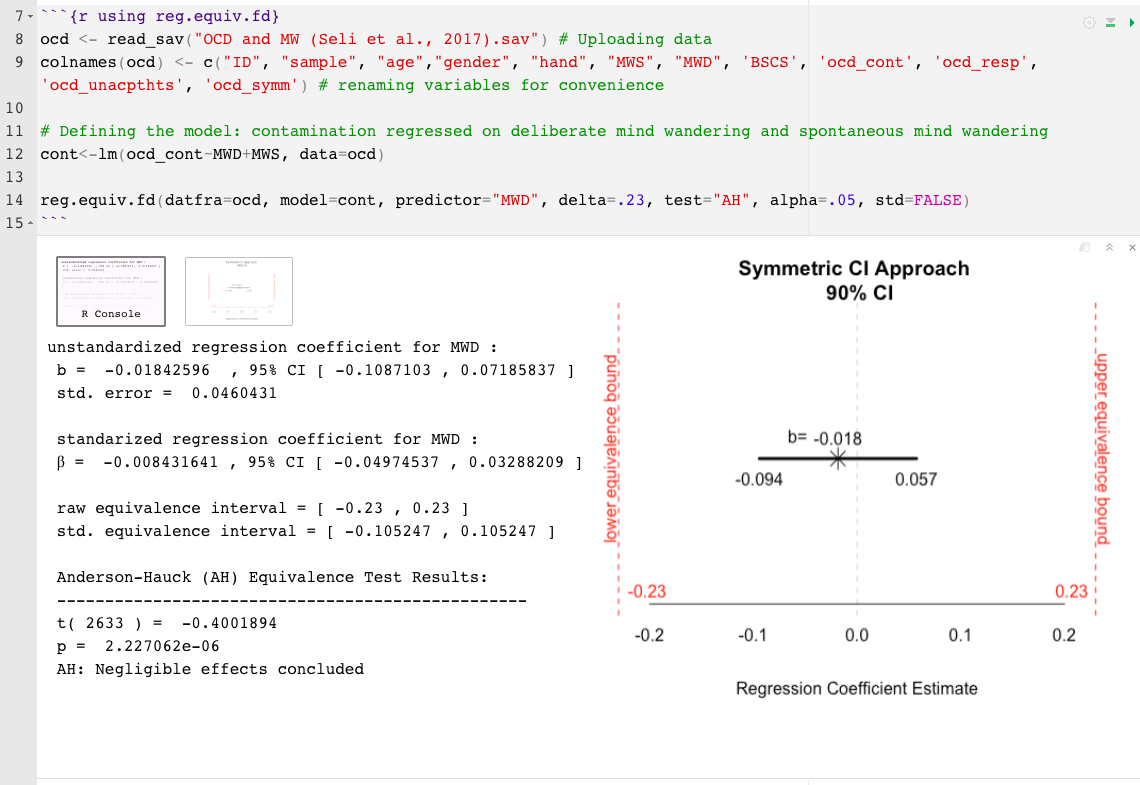
reg.equiv() : conjunto de dados completo não é necessáriob= o tamanho estimado do efeito associado ao preditor de interesse, isso pode ser padronizado ou não padronizado (por exemplo, 0,02)se= o erro padrão associado ao tamanho do efeito do preditor de interesse (se o tamanho do efeito for padronizado, verifique se o valor se está ligado ao efeito padronizado e não ao bruto)p= o número de preditores totais no modelo de regressão (excluindo a interceptação)n= tamanho da amostradelta= o menor tamanho de efeito de interesse (sesoi), tamanho de efeito minimamente significativo (MMES) ou limite superior do intervalo de equivalência (?) (Por exemplo, .15)predictor= o nome do preditor a ser testado (por exemplo, "cyl" )test= Tipo de teste é definido automaticamente para dois testes unilaterais (Tost; Schuirmann, 1987), a outra opção é o Anderson-Hauck (AH; Anderson & Hauck, 1983)std= o delta (ou, sesoi) e o tamanho do efeito indicado são definidos como padronizado por padrão. Indicar std=FALSE para assumir unidades não padronizadasalpha= A taxa de erro nominal do tipo I é definida como 0,05 por padrão. Para mudar, basta indicar o nível alfa. Por exemplo, alpha=.10 reg.equiv() Exemplo: 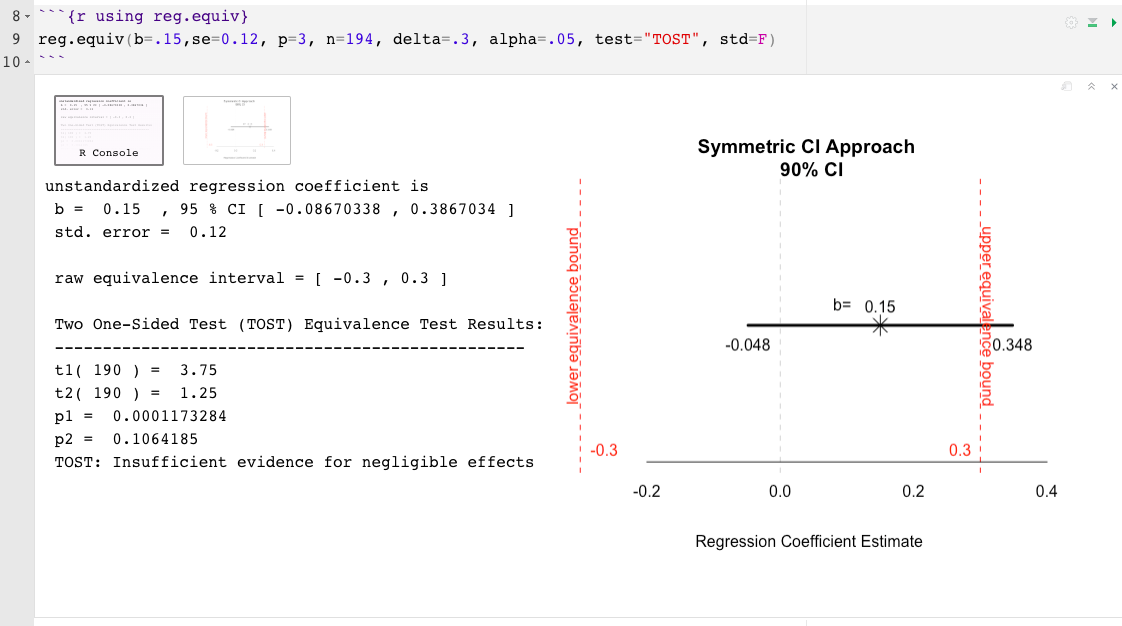
O teste de equivalência é um método projetado dentro da estrutura de teste de significância de hipótese nula (NHST). O NHST tem sido fortemente criticado por sua dependência excessiva dos resultados dicotômicos dos valores de P com pouco, ou nenhuma consideração da magnitude do efeito ou de suas implicações na prática (por exemplo, Cumming, 2012; Fidler & Loftus, 2009; Harlow, 1997; Kirk, 2003; 2003; Lee, 2016 2014). Os pesquisadores devem estar atentos às limitações do NHST e separar os aspectos práticos e estatísticos dos resultados dos testes.
Para minimizar as limitações dos valores de P , é mais informativo interpretar a magnitude e a precisão do efeito observado além da conclusão de "efeitos desprezíveis" ou "evidências insuficientes para efeitos insignificantes". Os efeitos observados devem ser interpretados em relação aos limites de equivalência, a extensão de sua incerteza e suas implicações práticas (ou falta dela) . Por esse motivo, as duas funções R oferecidas aqui também incluem uma representação gráfica do efeito observado e sua incerteza associada em relação ao intervalo de equivalência. A trama resultante ajuda a ilustrar o quão próximo ou largo ou estreito o efeito observado e sua margem de erro são dos limites de equivalência; Inferir sobre a proporção e posição da banda de confiança em relação ao intervalo de equivalência pode ajudar a interpretar os resultados acima e acima dos valores de P.