autodiff

AUTODIFF - Biblioteca C ++ de diferenciação automática

Este projeto mudou para o Boost (Math/Diferenciação/Autodiff) e este repositório não está mais sendo atualizado.

Construir status

Filial	Travis	AppVeyor	codecov.io
master
develop

Descrição

O Autodiff é uma biblioteca C ++ somente para cabeçalho que facilita a diferenciação automática (modo direto) das funções matemáticas de variáveis ​​únicas e múltiplas.

Esta implementação é baseada na expansão da série Taylor de uma função analítica f no ponto x₀ :

A idéia essencial do Autodiff é a substituição de números com polinômios na avaliação de F (x₀) . Substituindo o número x₀ pelo polinômio x₀+ε de primeira ordem e usando o mesmo algoritmo para calcular f (x₀+ε) , o polinômio resultante em ε contém os derivados da função f '(x₀) , f' '(x₀) , f '' '(x₀) , ... dentro dos coeficientes. Cada coeficiente é igual ao derivado de sua respectiva ordem, dividida pelo fatorial da ordem.

Em mais detalhes, suponha que se esteja interessado em calcular os primeiros n derivados de f em x₀ . Sem perda de precisão no cálculo dos derivados, todos os termos o (ε ⁿ⁺¹ ) que incluem poderes de ε maiores que n podem ser descartados. (Isso se deve ao fato de que cada termo em um polinomial depende apenas de termos iguais e de ordem inferior sob operações aritméticas.) Nessas regras de truncamento, F fornece uma transformação polinomial para polinomial:

A capacidade do C ++ de sobrecarregar os operadores e funções permite a criação de um fvar de classe que representa polinômios em ε . Assim, o mesmo algoritmo f que calcula o valor numérico de y₀ = f (x₀) , quando escrito para aceitar e retornar variáveis ​​de um tipo genérico (modelo), também é usado para calcular o polinomial ʃ _n y _n εⁿ = f (x₀+ ε) . Os derivados f ⁽ⁿ⁾ (x₀) são encontrados no produto do respectivo fatorial n! e coeficiente y _n :

Exemplo 1: diferenciação de variável única

 #include <boost/math/diferenciação/autodiff.hpp> #include <iostream> modelo <typename t>
T quarta_power (t const & x) {
  T x4 = x * x;  // retval no operador*() usa a memória do X4 via NRVO.
  x4 *= x4;      // Nenhuma cópia de X4 é feita dentro do operador*= () mesmo quando se quadrocinava.
  retornar x4;     // x4 usa a memória de y em main () via nrvo.} int main () {usando namespace boost :: math :: diferenciação;

  ordem não assinada constExpr = 5;                  // derivado de ordem mais alta a ser calculada.
  Auto const x = make_fvar <duplo, order> (2.0);  // Encontre derivados em x = 2.
  Auto const y = Fourth_Power (x);  para (não assinado i = 0; i <= order; ++ i)
    std :: cout << "y.Derivative (" << i << ") =" << y.Derivative (i) << std :: endl;  retornar 0;
}/*Saída: y.erivative (0) = 16y.Derivative (1) = 32y.erivative (2) = 48y.Derivative (3) = 48y.Derivative (4) = 24y.Derivative (5) = 0*//

O acima calcula

Exemplo 2: diferenciação multi-variável e multi-precisão

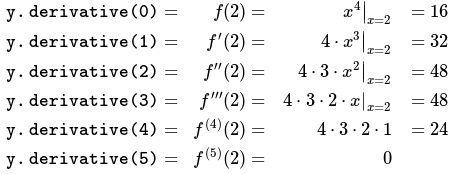
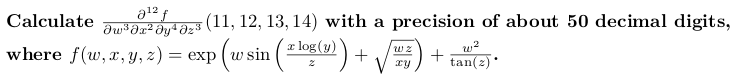
 #include <boost/math/diferenciação/autodiff.hpp> #include <boost/multiprecision/cpp_bin_float.hpp> #include <iostream> usando namespace boost :: math :: diferenciação; modelo <modelo w typename w, digitar x, tipename y, Typename Z>
promover <w, x, y, z> f (const w & w, const x & x, const y & y, const z & z) {usando namespace std;
  Retorno exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z);
} int main () {usando float50 = boost :: multiprecision :: cpp_bin_float_50;  constexpr não assinado NW = 3;  // Ordem máxima de derivado para calcular para W
  constexpr não assinado nx = 2;  // Ordem máxima de derivado para calcular para x
  constexpr não assinado NY = 4;  // Ordem máxima de derivado para calcular para y
  Constexpr não assinado NZ = 3;  // Ordem máxima de derivado para calcular para z
  // Declare 4 variáveis ​​independentes juntas em uma tupla std ::.
  Variáveis ​​automáticas const = make_ftuple <float50, nw, nx, ny, nz> (11, 12, 13, 14);  Auto const & w = std :: get <0> (variáveis);  // até derivados de NW em w = 11
  Auto const & x = std :: get <1> (variáveis);  // até derivados nx em x = 12
  Auto const & y = std :: get <2> (variáveis);  // até derivados de NY em y = 13
  Auto const & z = std :: get <3> (variáveis);  // até derivados da NZ em z = 14
  Auto const v = f (w, x, y, z);  // calculado a partir da diferenciação simbólica de Mathematica.
  Float50 const Answer ("1976.3196007477977717779881875290418720908121189218755");
  std :: cout << std :: setprecision (std :: numeric_limits <Float50> :: dígitos10)
            << "Mathematica:" << Responder << 'n' << "Autodiff:" << v.Derivative (nw, nx, ny, nz) << 'n' << std :: setprecision (3)
            << "Erro relativo:" << (v.Derivative (nw, nx, ny, nz) / resposta - 1) << 'n';  retornar 0;
}/*Output:mathematica   : 1976.3196007477977177798818752904187209081211892188autodiff      : 1976.3196007477977177798818752904187209081211892188relative error: 2.67e-50*/

Exemplo 3: Preços da opção de Black-Scholes com gregos calculados automaticamente

 #include <boost/math/diferenciação/autodiff.hpp> #include <tostream> usando o namespace boost :: math :: constants; usando namespace boost :: math :: diferenciação; // equações e nomes de função/variável são de //////// https://en.wikipedia.org/wiki/Greeks_(finance)#formulas_for_european_option_greeks// Função cumulativa normal de distribuição normal <Typename X>
X phi (x const & x) {return 0.5 * erfc (-one_div_root_two <x> () * x);
} classe enum cp {ligue, put}; // assume zero rendimento anual de dividendos (q = 0) .template <preço de tipo de tipo, tipo de tipo de tipo de tipo, typename tau, taxa de tipo de tipo de tipo>
Promover <Price, Sigma, Tau, Taxa> Black_Scholes_Option_price (CP CP, Double K,
                                                            Preço const & s,
                                                            Sigma Const & Sigma,
                                                            Tau Const & Tau,
                                                            Avaliar const & r) {usando namespace std;
  Auto const d1 = (log (s / k) + (r + sigma * sigma / 2) * tau) / (sigma * sqrt (tau));  Auto const d2 = (log (s / k) + (r - sigma * sigma / 2) * tau) / (sigma * sqrt (tau));  switch (cp) {case cp :: ligue: return s * phi (d1)-exp (-r * tau) * k * phi (d2); case cp :: put exp (-r * tau) * k * Phi (-d2)-s * phi (-d1);
  }
} int main () {duplo const k = 100.0;                    // Preço de ataque.
  Auto const S = make_fvar <duplo, 2> (105);  // Preço das ações.
  dupla const sigma = 5;                    // Volatilidade.
  const duplo tau = 30,0 / 365;             // Hora de expiração em anos. (30 dias).
  dupla const r = 1,25 / 100;               // Taxa de juro.
  Auto const call_price = Black_scholes_Option_Price (cp :: ligue, k, s, sigma, tau, r);  Auto const put_price = Black_scholes_Option_Price (cp :: put, k, s, sigma, tau, r);

  std :: cout << "Black-scholes de chamada preço =" << call_price.erivative (0) << 'n' << "Black-scholes put price = << put_price.derivative (0) << 'n' << "ligue para delta =" << call_price.derivative (1) << 'n' << "put delta =" << put_price.derivative (1) << 'n' << "ligue para gama =" << call_price .Derivative (2) << 'n' << "Coloque gamma =" << put_price.derivative (2) << 'n';  retornar 0;
}/*Saída: Preço de chamada preto-schóis = 56.5136black-scholes PUSCO PROCE = 51.4109CALL Delta = 0,773818put Delta = -0.226182 Gamma = 0,00199852 Gamma = 0,00199852*//

Consulte o exemplo/preto_scholes.cpp para obter uma lista maior de gregos de opção calculados automaticamente.

Vantagens da diferenciação automática

Os exemplos acima ilustram algumas das vantagens do uso do Autodiff:

• Eliminação da redundância do código. A existência de n funções separadas para calcular derivadas é uma forma de redundância de código, com todos os passivos que o acompanham:

• Alterações em uma função requerem n alterações adicionais em outras funções. No terceiro exemplo acima, considere quanto maior e interdependente a base de código acima seria se uma função separada fosse gravada para cada valor grego.

• As dependências de uma função derivada para um propósito diferente serão interrompidas quando as alterações forem feitas na função original. O que não precisa existir não pode quebrar.

• Código inchaço, reduzindo a integridade conceitual. O controle sobre a evolução do código é mais fácil/mais seguro quando a base de código é menor e capaz de ser intuitivamente compreendida.

• Precisão dos derivados sobre métodos de diferença finita. Os métodos de diferença finita de uma das Único sempre incluem uma variável livre Δx que deve ser cuidadosamente escolhida para cada aplicação. Se Δx for muito pequeno, os erros numéricos se tornarão grandes. Se Δx for muito grande, os erros matemáticos se tornarão grandes. Com o Autodiff, não há variáveis ​​livres a serem definidas e a precisão da resposta é geralmente superior aos métodos de diferença finita, mesmo com a melhor escolha de Δx .

Manual

Detalhes adicionais estão no manual do Autodiff.

Licença

Distribuído sob a licença de software Boost, versão 1.0.

Propriedades

• Apenas cabeçalho.

• Otimizado para C ++ 17. Também compila e testado com os padrões C ++ 11, C ++ 14 e propostos C ++ 20.

• Toda a memória é alocada na pilha.

Diretórios

Nome	Propósito
doc	documentação
example	exemplos
include	cabeçalhos
test	Testes de unidade

Mais informações

• Bugs de relatório: Certifique -se de mencionar a versão, a plataforma e o compilador que você está usando. Um pequeno exemplo de código compilável para reproduzir o problema também é sempre bom.

• Envie seus patches como solicitações de tração contra a filial Desenvolvimento. Observe que, ao enviar patches, você concorda em licenciar suas modificações sob a licença de software Boost, versão 1.0.