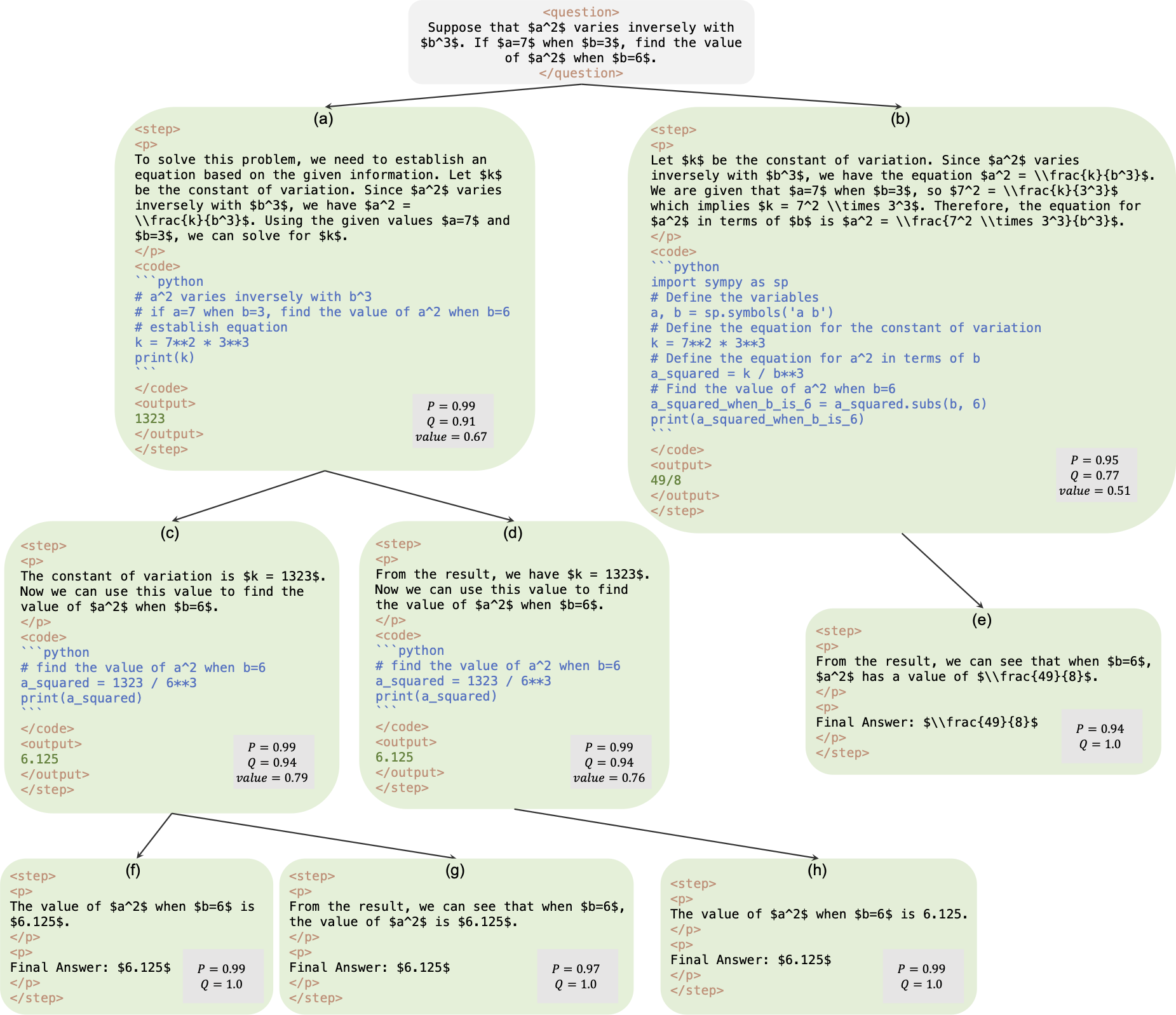
Это официальный репозиторий статьи AlphaMath Почти ноль: надзор за процессом без процесса. Код извлекается из нашей внутренней корпоративной базы кода. В результате при воспроизведении цифр, приведенных в нашей статье, могут быть небольшие различия, но они должны быть очень близкими. Наш подход предполагает обучение моделей политик и ценностей с использованием только математических рассуждений, полученных из структуры поиска по дереву Монте-Карло (MCTS), что устраняет необходимость в GPT-4 или человеческих аннотациях. Это иллюстрация обучающего экземпляра, созданного MCTS в третьем раунде.
Контрольная точка : AlphaMath-7B, раунд 3? / AlphaMath-7B тур 3 ?
Набор данных : AlphaMath-Round3-Trainset? Процесс решения обучающих данных автоматически генерируется на основе MCTS и контрольной точки в раунде 2. Для обучения моделей политики и стоимости включены как положительные, так и отрицательные примеры.
Учебный код : в соответствии с политикой мы можем публиковать только детали реализации некоторых ключевых функций, которые в основном должны быть изменены в вашем собственном обучающем коде.
| Метод вывода | Точность | средн. время (с) за q | средн. шаги | # сол |
|---|---|---|---|---|
| Жадный | 53,62 | 1,6 | 3.1 | 1 |
| май@5 | 61,84 | 2,9 | 2,9 | 5 |
| Балка ступенчатого уровня (1,5) | 62,32 | 3.1 | 3.0 | топ-1 |
| 5 заездов + май@5 | 67.04 | х5 | х1 | 5 топ-1 |
| Балка ступенчатого уровня (2,5) | 64,66 | 2.4 | 2.4 | топ-1 |
| Балка ступенчатого уровня (3,5) | 65,74 | 2.3 | 2.2 | топ-1 |
| Балка ступенчатого уровня (5,5) | 65,98 | 4.7 | 2.3 | топ-1 |
| 1 заезд + май@5 | 66,54 | х1 | х1 | топ-5 |
| 5 заездов + май@5 | 69,94 | х5 | х1 | 5 топ-1 |
| МСТС (N=40) | 64.02 | 10.1 | 3,8 | топ-1 |
+ Maj@5 требует запуска 5 раз, что способствует разнообразию.+ Maj@5 напрямую использует 5 кандидатов, которым не хватает разнообразия.| температура | 0,6 | 1.0 |
|---|---|---|
| Балка ступенчатого уровня (1,5) | 62,32 | 62,76 |
| Балка ступенчатого уровня (2,5) | 64,66 | 65,60 |
| Балка ступенчатого уровня (3,5) | 65,74 | 66,28 |
| Балка ступенчатого уровня (5,5) | 65,98 | 66,38 |
Для поиска луча на ступенчатом уровне установка temperature=1.0 может привести к несколько лучшим результатам.
requirements.txt pip install -r requirements.txt
Или просто следуйте cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py чтобы добавить заголовок значения в LLM. Вы можете запустить любой из следующих двух cmds. Между ними может быть небольшая разница в точности. В нашей машине первый получил 53,4%, а второй 53,62%.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
или
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
На нашей машине, на тестовом наборе MATH, следующая команда с конфигурацией B1=1, B2=5 может достичь ~62%, а команда с конфигурацией B1=3, B2=5 может достичь ~65%.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Рассчитайте точность
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
ground_truth (окончательный ответ, а не процесс решения) должен быть предоставлен в файле qaf json или jsonl (пример формата может относиться к ../MARIO_EVAL/data/math_testset_annotation.json ).
раунд 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
раунд > 1, после SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
Для генерации решения будет использоваться только question , но для расчета точности будет использоваться ground_truth .
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
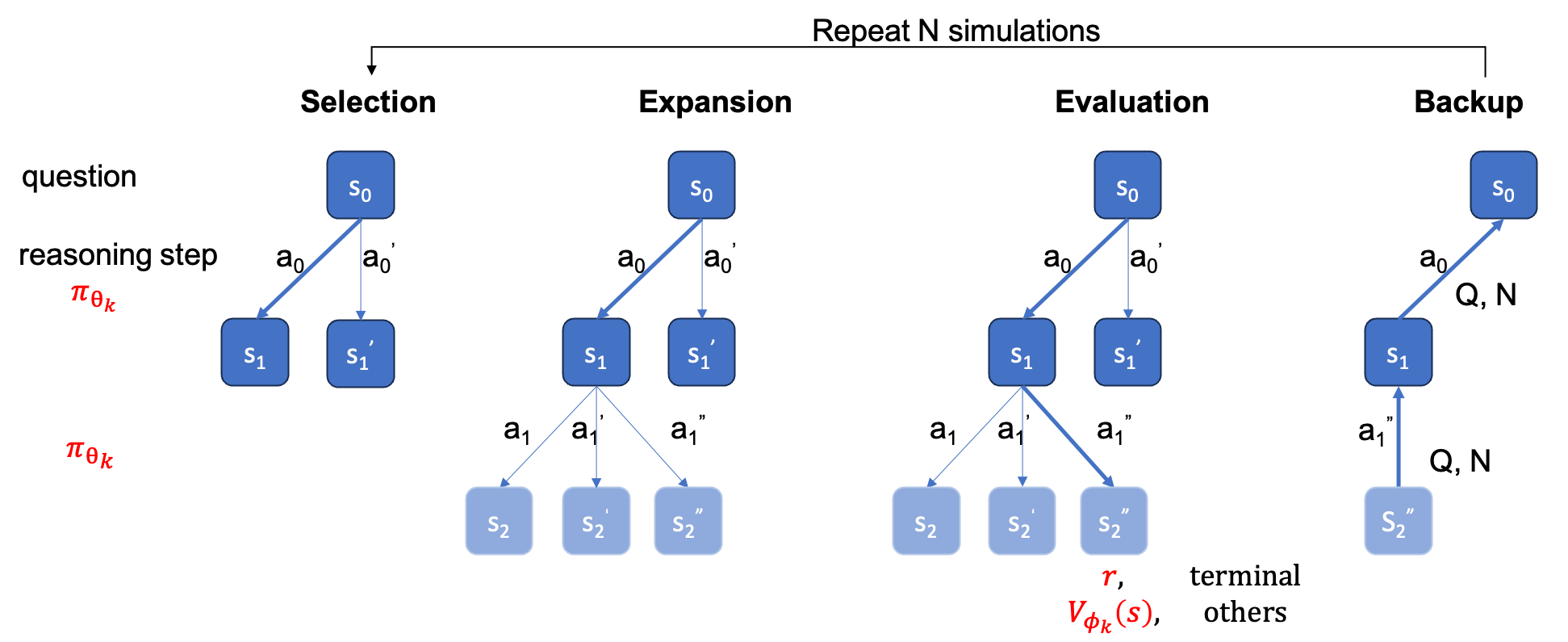
В отличие от поиска луча на уровне шага, вам нужно сначала построить полное дерево, затем запустить MCTS в автономном режиме и рассчитать точность.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
Примечание. Этот сценарий оценки также можно запустить с сохраненным деревом путем пошагового поиска луча, при этом точность должна оставаться той же.
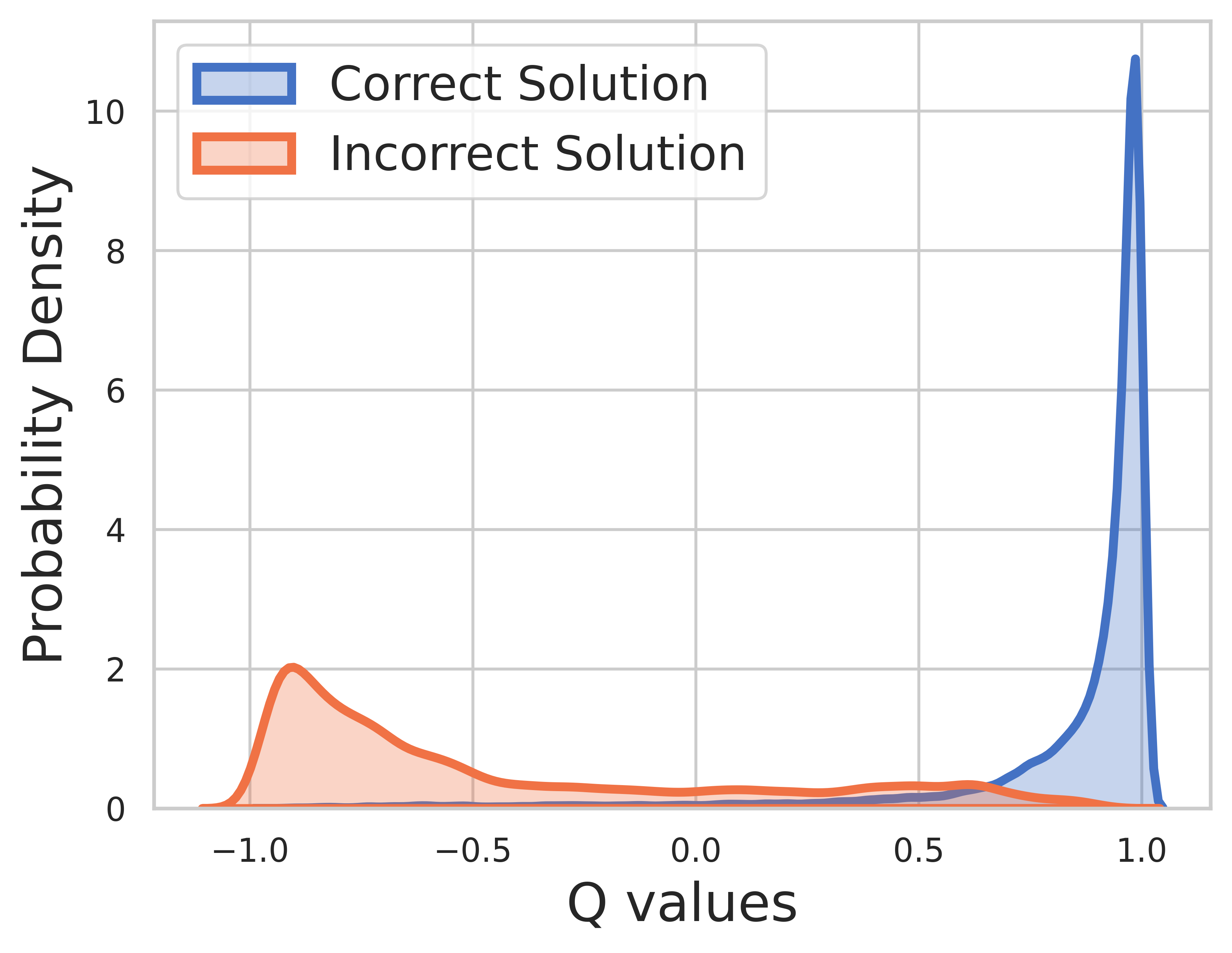
Поскольку основная истина известна для обучающих данных, ценность последнего шага — это вознаграждение, и значение Q может очень хорошо сходиться.
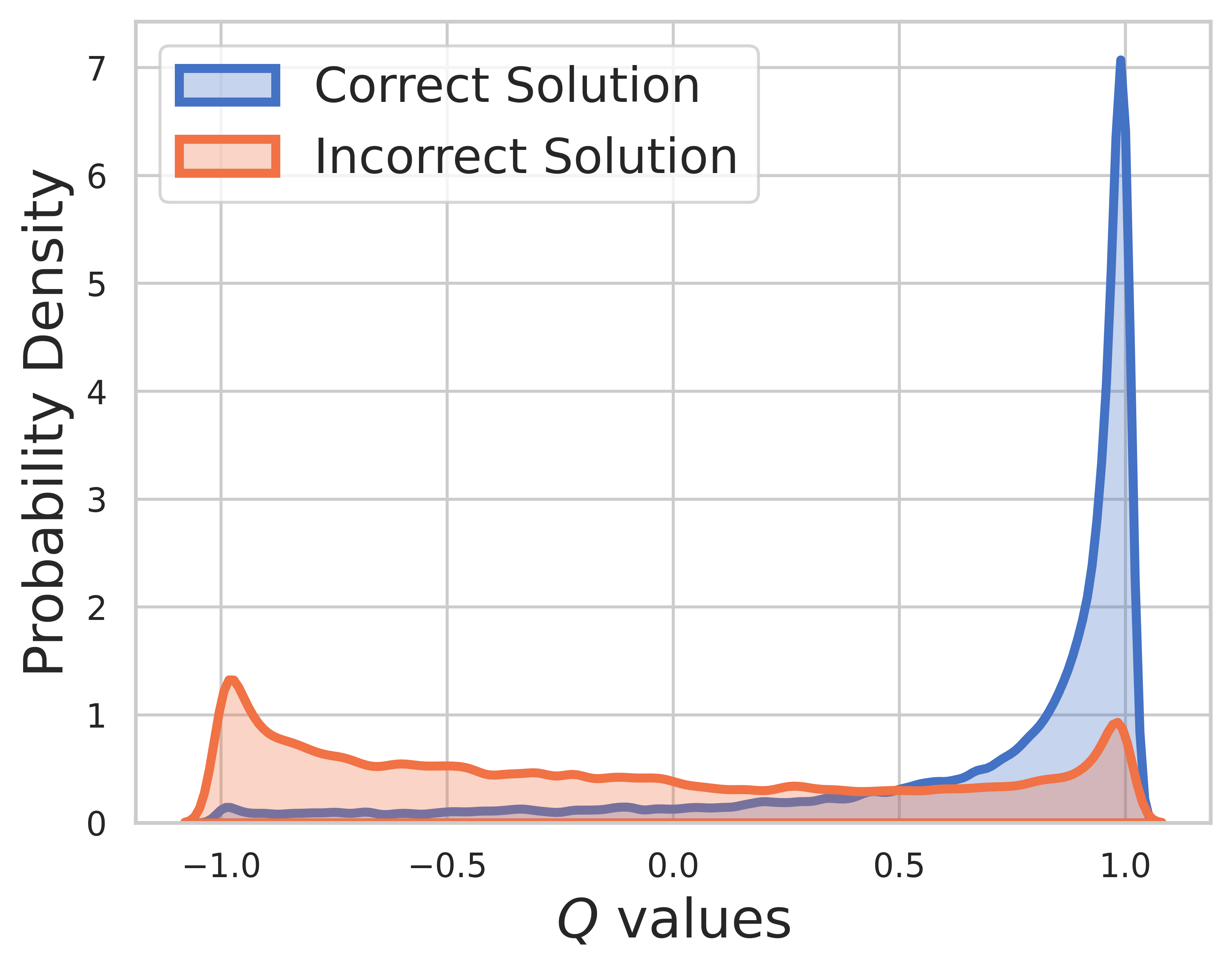
На тестовом наборе основная истина неизвестна, поэтому распределение значений Q включает как промежуточные, так и заключительные этапы. Из этого рисунка мы можем найти
СВПО от МЦТС
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
версия МКТС
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
Инструментарий оценки
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
Версия OVM (модель конечного значения)
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}