Повторная выборка Ланчоса (произносится как Ланчос) — это сложный метод интерполяции цифровых сигналов, обеспечивающий превосходное качество изображения по сравнению с более простыми методами, такими как метод ближайшего соседа и билинейная интерполяция. Благодаря эффективному сохранению деталей и минимизации артефактов сглаживания, передискретизация Ланцоша широко используется в приложениях обработки изображений и сигналов.
Хотя Ланцос превосходит качество изображения, за это приходится платить повышенной вычислительной сложностью. Кроме того, недостатком может быть возможность появления «звенящих» артефактов, особенно вокруг острых краев. Несмотря на эти проблемы, Lanczos остается предпочтительным выбором для таких задач, как масштабирование и поворот изображения, благодаря его общим преимуществам в производительности.
В этом документе представлен всесторонний обзор повторной выборки Ланцоша, включая ее теоретическую основу, детали реализации и практическое применение. Он служит ценным ресурсом для разработчиков и исследователей, стремящихся понять и использовать эту мощную технику. В последующих разделах рассматриваются важные аспекты повторной выборки Ланцоша, такие как ядро Ланцоша, процессы интерполяции и повторной выборки, сохранение потока, повышающая и понижающая дискретизация, расположение выборки, выходной диапазон, многомерная интерполяция и разделимость. Включен практический пример с сопроводительным исходным кодом.
Ядро Ланцоша, определенное для заданного размера поддержки, представляет собой функцию, используемую при повторной выборке Ланцоша. Ядро определяется как:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
Где:
Нормализованная функция sinc определяется как:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
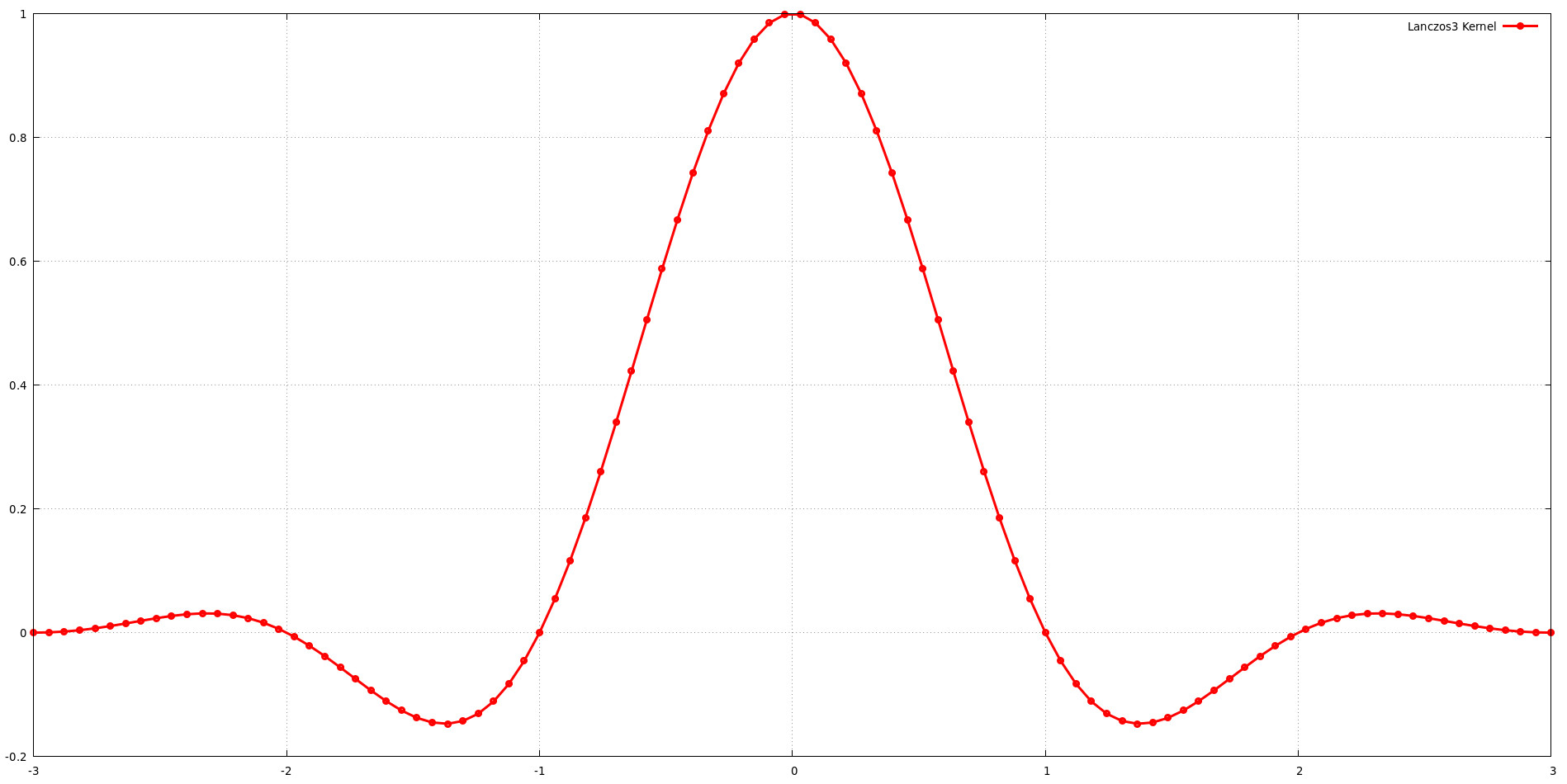
График иллюстрирует форму ядра Ланцоша для размера опоры a = 3. Это означает, что ядро включает три доли функции sinc. Хотя увеличение размера опоры (а) обычно обеспечивает большую гибкость при формировании частотной характеристики, оно также увеличивает вычислительные затраты. При выборе размера опоры необходимо найти баланс между качеством изображения и эффективностью вычислений. Открытие Джима Блинна о том, что ядро Ланцоша с = 3 предлагает превосходный баланс сохранения низких частот и подавления высоких частот, подтверждает это мнение.
Примечание. Термины «ширина ядра», «размер поддержки» и «размер фильтра» часто используются как взаимозаменяемые для описания параметра a. Однако в контексте повторной выборки Ланцоша «размер поддержки» наиболее точно отражает концепцию.
Интерполяция Ланцоша — это метод, используемый для повторной дискретизации дискретного сигнала до новой частоты дискретизации. Это достигается путем свертки исходного сигнала с ядром Ланцоша.
Интерполированный сигнал s2(x) можно рассчитать следующим образом:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
Где:
Сохранение флюса:
Коэффициент нормализации w(x) имеет решающее значение для сохранения общей энергии или массы сигнала во время процесса интерполяции. Это гарантирует, что сумма интерполированных значений приближается к сумме исходных выборок. Вес фильтра рассчитывается как:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
Повышение дискретизации:
При увеличении частоты дискретизации уравнение интерполяции Ланцоша можно использовать напрямую без модификаций.
Понижение разрешения:
Чтобы избежать артефактов наложения спектров при уменьшении частоты дискретизации, масштаб фильтра необходимо настроить в соответствии с новой частотой дискретизации.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
Где:
При повторной дискретизации сигнала из n1 выборок в n2 выборок используются следующие позиции выборок. Индекс j используется для представления выборок из дискретизированного сигнала s2(x). Член (j + 0,5) — это центр выборки в s2(x). Этот шаг масштабирует точку в s2(x) до точки в s1(x). Последний член -0,5 в x представляет собой фазовый сдвиг, который приводит к смещению выборок коэффициента Ланцоша.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
При выполнении интерполяции Ланцоша особое внимание необходимо уделять границам сигнала. Общие методы обработки кромок включают в себя:
Нулевое заполнение:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
Зажим:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
Зажим часто предпочтительнее, поскольку он уменьшает краевые артефакты, вызванные резкими разрывами вблизи краев. Однако выбор метода обработки кромок зависит от конкретного применения и желаемого результата.
Диапазон s2(x) может быть больше, чем диапазон s1(x) из-за лепестков L(x). Например, входной сигнал s1(x), соответствующий цветам пикселей в диапазоне [0.0,1.0], необходимо ограничить одним и тем же диапазоном, чтобы гарантировать, что выходные значения не переполнятся при преобразовании обратно в беззнаковые байты [0,255]. .
Ядро Lanczos можно расширить до нескольких измерений для выполнения интерполяции изображений или многомерных данных.
Двумерное ядро Ланцоша определяется как:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
Интерполированный сигнал s2(x, y) можно рассчитать по следующей формуле:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
Где w(x, y) — коэффициент нормализации, рассчитанный с использованием двумерного ядра Ланцоша.
В отличие от некоторых методов интерполяции, ядро Ланцоша неразделимо, то есть его нельзя разложить на произведение одномерных ядер. Это свойство обычно приводит к более высоким вычислительным затратам по сравнению с сепарабельными ядрами. Чтобы повысить производительность, некоторые реализации аппроксимируют ядро Lanczos, выполняя отдельные проходы для горизонтальных и вертикальных измерений.
Горизонтальная интерполяция:
Вертикальная интерполяция:
Математическое представление:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
Обратите внимание, что коэффициенты нормализации w(x) и w(y) рассчитываются с использованием одномерного ядра Ланцоша.
Ключевые моменты:
Аналогичным образом, многократная рекурсивная передискретизация сигнала, как это обычно делается для создания MIP-карт текстур, также может ухудшить качество изображения из-за накопления ошибок на каждом этапе повторной выборки.
Запустите пример lancos-test и используйте gnuplot, чтобы увидеть, как передискретизация Ланцоша влияет на простой одномерный сигнал при повышении и понижении дискретизации в 2 раза.
make
./lanczos-test
gnuplot
> load "output.plot"
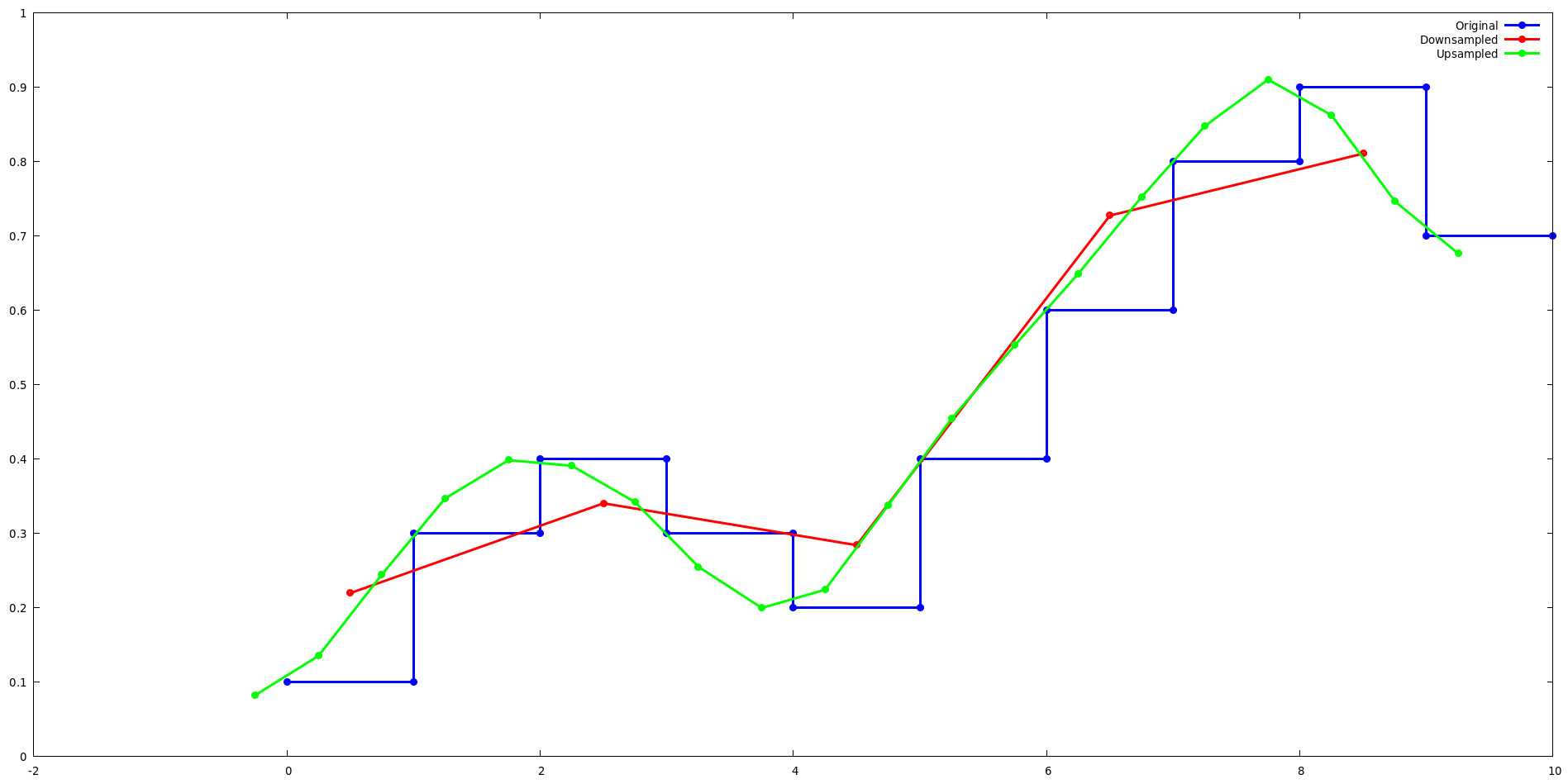
Повышение дискретизации:
При повышении дискретизации на степень двойки ядро Ланцоша циклически переключается между наборами значений уровня 2^. Например, рассмотрим первые 4 вывода примера повышения дискретизации lanzcos-test. Обратите внимание, что выходные данные для L(x) повторяются для j={0,2} и j={1,3}.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
Понижение разрешения:
При понижающей дискретизации в степени двойки ядро Ланцоша становится независимым от x, поскольку (x - Floor(x)) становится константой, соответствующей фазовому сдвигу. Например, рассмотрим первые два результата примера понижающей выборки lanzcos-test. Обратите внимание, что выходные данные L(x) повторяются для каждого j.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
В качестве дополнительной оптимизации для этих случаев можно заранее рассчитать ядро Ланцоша, чтобы исключить дорогостоящее вычисление функции sinc.
Этот README был создан при содействии Google Gemini.
Дополнительные ссылки включают:
Этот код был реализован Джеффом Буди по лицензии MIT.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.